高抗噪性三维体曲率分析技术及其在高陡地层发育区的应用
王清振,姜秀娣,翁 斌,丁继才,陈剑军
(中海油研究总院,北京100028)
高抗噪性三维体曲率分析技术及其在高陡地层发育区的应用
王清振,姜秀娣,翁 斌,丁继才,陈剑军
(中海油研究总院,北京100028)
曲率属性可以较好地描述岩层的弯曲、褶皱、断层和裂缝等信息,但是由于曲率属性提取过程中需要计算地震数据的二阶微分,因此对噪声比较敏感,影响了结果的稳定性和可信度。在模型试算的基础上,提出了一种新的高抗噪性的体曲率计算方法。首先利用小波变换方法提取三维地震资料的相位余弦体;然后基于复地震道理论计算三维体视倾角属性,对视倾角进行中值滤波以压制微分计算中生成的噪声;最后利用两个方向的视倾角属性计算得到各类高信噪比的体曲率属性。模型实验和实际资料处理结果表明,该方法计算的曲率属性对噪声不敏感,适用于低信噪比资料的处理,特别是在陡倾角地层发育的地区,计算结果比C3等相干属性假象更少,能够真实地反映地下断层及岩性边界等地质信息。
断层检测;曲率;相位余弦;相干;小波变换
曲率属性分析是近年来兴起的一种利用地层的弯曲程度进行不连续性检测的方法,与相干算法相比,该方法对复杂河道、裂缝,小断层及褶皱的刻画能力更为优越[1-2]。LISLE[3]对高斯曲率与裂缝的相关性进行了研究,验证了曲率和裂缝之间的对应关系;ROBERTS[4]对地震曲率属性进行了系统的分类,并阐述了多种曲率属性如平均曲率、高斯曲率、极大曲率、极小曲率、最大正曲率和最小负曲率的定义以及各自的特点,给出了利用解释的地质层位计算二维曲率的方法。但由于人工解释的地质层位存在偏差,计算的曲率准确性受到很大影响,容易引起构造假象。为此AL-DOSSARY等[5]提出了三维体曲率的计算方法,它首先利用原始地震资料的振幅信息计算地层倾角,然后通过相似性扫描的方法来计算曲面的一阶导数,将曲率算法从二维推广到三维。
国内学者近年来也对曲率属性进行了大量研究,CHEN等[6]利用小波变换对曲率属性进行了多尺度分解,并将得到的多个尺度的曲率属性进行融合显示,提高了大断层和小断层的综合显示能力;GAO[7]提出了一种用于小断层识别的梯度曲率属性,取得了较好效果;王世星[8]和印兴耀等[9]给出了一种基于倾角扫描的体曲率提取方法;QI等[10]给出了断层控制的喀斯特地区的曲率属性特征。杨国权等[11]、李福强等[12]分别用5×5,7×7网格来拟合二次曲面以期得到更高精度的曲率属性,并将其权系数表示成微分算子的形式来提高其运算效率。
当前,三维体曲率属性已成为继相干技术之后的又一大热点应用技术[13],尤其在河道及裂缝型油气储层预测中效果显著[14]。但是由于曲率计算过程中要对地震数据求两次微分运算,而微分运算对噪声较为敏感,因而严重影响了曲率属性的实际应用效果。本文提出了一种新的体曲率计算方法,首先利用连续小波变换方法提取三维地震资料的相位余弦体,然后基于复数道分析理论,采用CLAERBOUT[15]提出的差分算法计算瞬时频率和x,y方向的瞬时波数,进一步计算三维地震数据体的视倾角,最后应用中值滤波后的视倾角数据计算各类曲率属性。模型实验和实际资料处理结果表明:①该方法对噪声不敏感,可以应用于低信噪比资料;②该算法计算得到的曲率属性与C3等相干属性相比假象更少,能够真实地反映地下断层及岩性边界等地质信息,特别适用于陡倾角地层发育的地区。
1 技术原理
1.1 基于小波变换相位余弦属性提取
实地震道x(t)的小波变换定义为:
(1)

(2)

(3)
(4)
(5)
式中:Re[c(t)]和Im[c(t)]分别表示c(t)的实部和虚部。利用相位属性可以很方便地计算出相位余弦属性cos[φ(t)]。
因为直接利用上述公式计算的瞬时属性与Hilbert方法计算的瞬时属性是等价的,所以对于含噪信号,在利用小波变换得到WΨ(t,a)之后,本文首先在小波变换域确定有效信号的能量分布空间,然后再利用公式(3)到公式(5)计算瞬时属性,从而提高了瞬时属性的信噪比,为后续视倾角的提取提供了高品质基础资料。
1.2 基于复数道分析理论计算视倾角
由地下三维空间中任一反射点r(t,x,y)处得到的相位余弦数据可以看作是时间标量u(t,x,y),其梯度grad(u)表示该点处反射面上沿着方向矢量所在的法截面截取曲线的一阶导数,即反射面沿着不同方向的变化率,可以用下式表示[19-20]:

(6)
式中:px,qy,rt表示反射点r处地震记录u沿x,y和t方向上的视倾角分量(见图1)。图1中,φ为方位角,θ为真倾角。
曲率是描述曲线上任意一点弯曲程度的一种属性,在数学上可定义为曲线上某点处角度与弧长变化率之比,也可表示为该点的二阶微分[21]:
(7)
式中:α是角度;s是弧长。代入视倾角px,qy,得到沿x方向和y方向的曲率分量:
(8a)

图1 三维空间中视倾角与倾角和方位角的关系[5]
(8b)
由此可知,要计算体曲率,需要先求取视倾角数据体。有多种求取视倾角的方法,可以通过倾角扫描或梯度结构张量方法计算[22-24],也可以采用复数道分析理论方法[25-26],利用瞬时频率和x,y方向的瞬时波数来计算三维地震数据体的视倾角。
其中,瞬时频率ω,x和y方向的瞬时波数kx和ky分别为:
(9)
式中:φ为瞬时相位;φx和φy为沿着x和y方向的空变相位;u为输入的相位余弦数据;uH为其时间方向的Hilbert变换。
从(9)式可看出,计算瞬时频率、瞬时波数时需要对初始地震数据及其Hilbert变换求二阶偏导数,这类运算对噪声非常敏感,因此,本文按下式计算瞬时频率:
(10)
式中:z(t)为初始信号的解析信号;Δt为信号的采样间隔。
为了提高计算精度,对(10)式表示的方法进行改进,利用中心差分格式,并将虚部运算化为实部,得到瞬时频率的实现公式为:
u(t)-[u(t+Δt)-u(t-Δt)h(t)}/[u2(t)+
h2(t)]
(11)
式中:u(t)为输入相位余弦数据;h(t)为其相应的Hilbert变换。
同理可得沿x和y方向的瞬时波数kx,ky的实现公式:

(12)
视倾角(px,qy)可利瞬时波数kx,ky和瞬时频率ω进行计算:
(13)
由于计算过程中有微分运算,因此求得的视倾角数据常常存在较大的噪声和突变点。为解决这个问题,本文应用中值滤波的方法对视倾角数据进行预处理,提高了倾角属性的信噪比,从而能够增强后续曲率属性提取的稳定性和平面效果。
1.3 曲率属性提取
在三维空间中,任一点的曲率值可以利用其相邻道和样点的视倾角值拟合的空间曲面方程来计算,基于最小二乘逼近原理,N次曲面拟合方程如下[4]:
(14)
当N=2时,将方程系数置换,得到二次曲面方程:
z(x,y)=ax2+by2+cxy+dx+ey+f
(15)
方程的系数为:
(16)
因此,可以利用(16)式中的5个系数计算三维地震数据中每一点的曲率。在过三维空间任一点的曲面上有很多种曲率属性,其中比较常用的曲率属性有平均曲率、高斯曲率、最大正曲率和最小负曲率等,其数学含义及地质含义见表1。

表1 各类曲率属性数学含义及地质含义
2 数值实验
为了验证上述技术对河道和断层的检测能力以及对资料信噪比的适应性,本文对包含河道和推覆构造的推覆体模型进行了实验。纵测线和横测线都是401道,纵向185ms,采样间隔1ms。图2a是第320条横测线(Xline320)速度剖面,可以看出推覆体模型含有高角度地层、多条断层和河道等地质信息,可以用来检测算法对倾斜地层、断层和小河道的检测能力。图2b是应用主频为30Hz的子波得到的正演模型地震剖面,可以看到,由于主频较低,河道信息在地震记录上不是很明显。用常规C3相干算法和本文提出的算法分别进行了不连续性检测,图2c是本文方法计算的最小负曲率结果,图2d是C3相干算法检测结果,可以看出,C3相干算法受地层结构影响较为强烈,大倾角地层存在较强的层间不连续性信息,影响了平面上断层和河道的检测。通过对比可以看出,图2d中a点和b点处的不连续性是由大倾角地层引起的,不是真实的断层和岩性边界,c点和e点是真实的断层信息。图2c中消除了倾斜地层的影响,只有c点和e点处的断层被检测出来,如实地反映了真实的断层和河道等地质体边界信息。其中d点处虽然曲率较大也被检测出来,说明曲率属性既能检测断层,也能检测褶皱等地质信息。
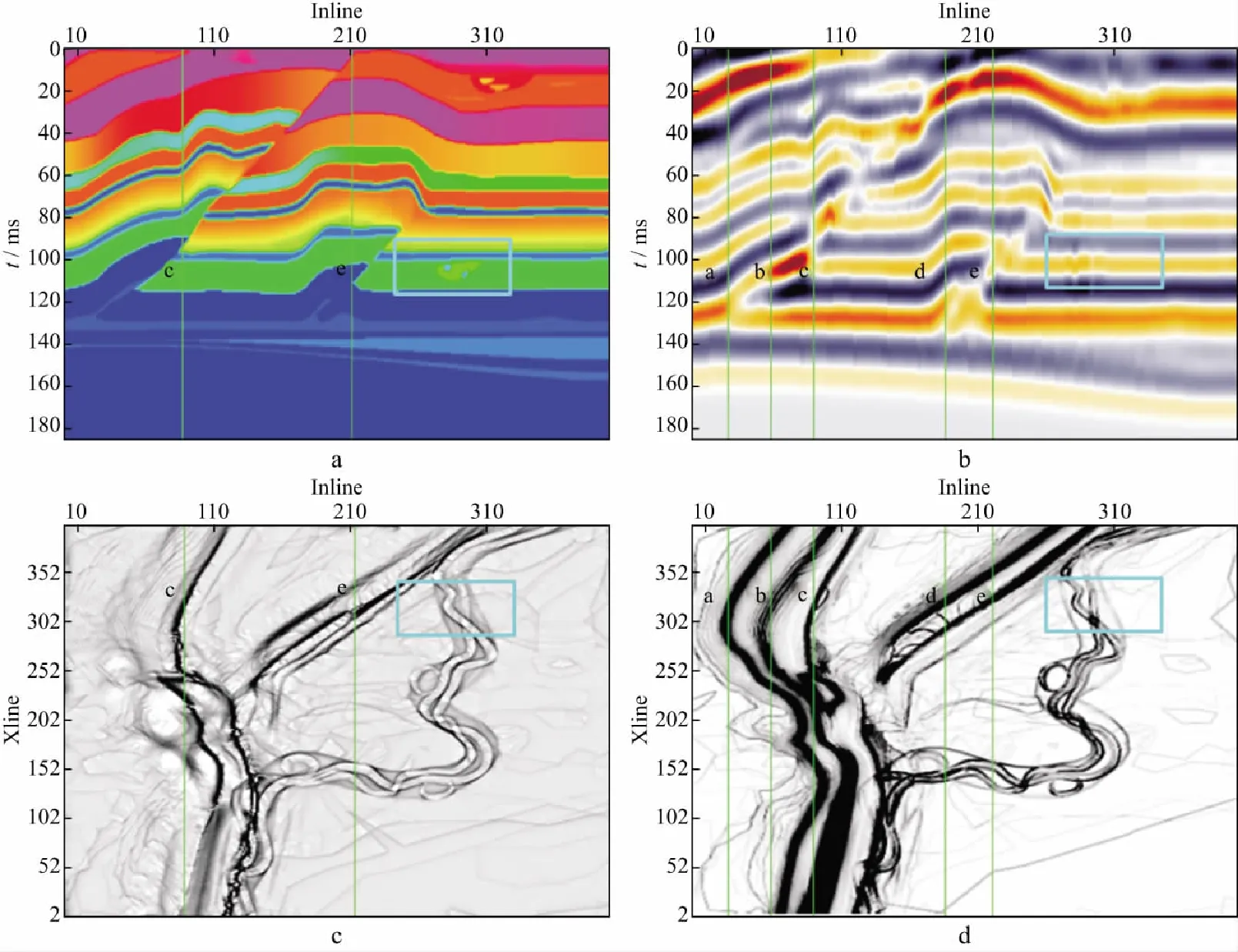
图2 推覆体模型及其不连续性检测效果a 三维模型Xline320线的速度剖面; b 对应的地震剖面; c 本文方法计算的最小负曲率100ms处时间切片; d C3相干算法计算结果100ms处时间切片
为检验本文曲率分析技术的抗噪性,对正演地震记录加入部分高斯白噪声,并基于小波变换求取了相位余弦属性,然后对原始数据(图3a)、含噪数据(图3b)和相位余弦数据(图3c)分别用本文算法和C3相干算法进行不连续性检测。图3d,图3e和图3f是C3相干算法计算结果,图3g,图3h和图3i是本文算法计算结果。对比发现,C3相干算法对噪声要敏感得多,无论是含噪数据还是相位余弦数据,检测结果中河道边界都非常模糊,特别是左下方河道与断层交错的位置(红色方框内),河道边界不可辨识。而本文方法基于相位余弦数据计算的结果信噪比较高,在本文如此大的噪声背景下仍然能够较好地刻画出河道的边界信息。

图3 基于推覆体模型的本文曲率分析技术抗噪性实验a 原始数据; b 含噪数据; c 相位余弦数据; d 原始数据C3相干算法计算结果; e 含噪数据C3相干算法计算结果; f 相位余弦数据C3相干算法计算结果; g 原始数据本文算法计算结果; h 含噪数据本文算法计算结果; i 相位余弦数据本文算法计算结果
3 实际应用
利用南海某油田断层和高陡地层比较发育的实际地震资料进行试验处理,分别提取C3相干属性和曲率属性。图4是三维地震数据的一条任意测线剖面,左侧地层较平,中间发育高陡地层,右侧发育大量断层。图5是4100ms处C3相干时间切片和地震任意测线的三维显示结果,可以看出,中部高陡地层发育区(箭头指示区)用C3相干算法识别为断层,所以该区域显示出一团强烈的不相干性,无法判断断层位置,右侧断层发育区用C3相干算法识别的结果与实际剖面不太吻合,因为该区部分地层倾斜角度也比较大。图6是曲率K1属性的切片和地震剖面共同显示的结果,可以看出,中部陡倾角地层发育区(箭头指示区)曲率切片非常干净,没有显示出不连续性,和地层实际情况吻合较好,右侧断层发育区切片和剖面在断点处较一致。说明曲率属性在陡倾角地层发育的地区有着非常好的应用效果,而用相干属性方法则无法达到这个效果。

图4 实际地震剖面

图5 4100ms处C3相干时间切片与地震剖面
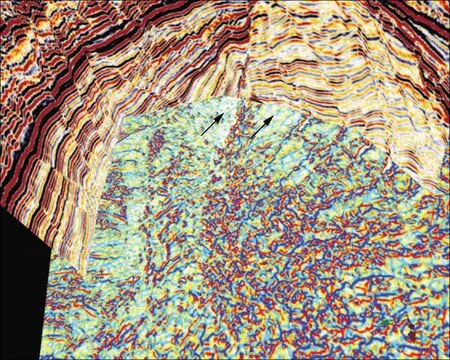
图6 4100ms处曲率K1时间切片与地震剖面
4 结束语
本文利用小波变换计算相位余弦属性,在此基础上计算多种曲率属性和角度属性,进行断层、河道等地质体边缘信息的检测。该项技术能够充分利用三维地震资料的空间信息计算地层的三维弯曲程度。与传统相干算法相比,能够有效地去除高倾角地层对断层检测的影响,得到合理可靠的检测结果,特别适用于在陡倾角地层发育的地区进行不连续性检测。
此外,由于采用了相位余弦计算、视倾角中值滤波等处理技术,该算法具有良好的抗噪性,适用于低信噪比数据。当然,在进行曲率分析之前,如果能进行必要的保边缘去噪处理,检测效果可能会更好。
致谢:感谢中国石油大学(北京)袁三一博士提供推覆体模型数据,感谢成都理工大学陈学华教授在曲率认识方面进行的有益探讨。
[1] CHOPRA S,MARFURT K J.Curvature attribute applications to 3D surface seismic data[J].The Leading Edge,2007,26(4):404-414
[2] CHOPRA S,MARFURT K J.Emerging and future trends in seismic attributes[J].The Leading Edge,2008,27(3):298-318
[3] LISLE R J.Detection of zones of abnormal strains in structures using Gaussian curvature analysis[J].AAPG Bulletin,1994,78(12):1811-1819
[4] ROBERTS A.Curvature attributes and their application to 3D interpreted horizons[J].First Break,2001,19(2):85-100
[5] AL-DOSSARY S,MARFURT K J.3D volumetric multispectral estimates of reflector curvature and rotation[J].Geophysics,2006,71(5):41-51
[6] CHEN X H,YANG W,HE Z H,et al.The algorithm of 3D multi-scale volumetric curvature and its application[J].Applied Geophysics,2012,9(1):65-72
[7] GAO D L.Integrating 3D seismic curvature and curvature gradient attributes for fracture characterization:methodologies and interpretational implication[J].Geophysics,2013,78(2):O21-O31
[8] 王世星.高精度地震曲率体计算技术与应用[J].石油地球物理勘探,2012,47(6):965-972 WANG S X.High-precision calculation of seismic volumetric curvature attributes and its application[J].Oil Geophysical Prospecting,2012,47(6):965-972
[9] 印兴耀,高京华,宗兆云.基于离心窗倾角扫描的曲率属性提取[J].地球物理学报,2014,57(10):3411-3421 YIN X Y,GAO J H,ZONG Z Y.Curvature attribute based on dip scan with eccentric window[J].Chinese Journal of Geophysics,2014,57(10):3411-3421
[10] QI J,ZHANG B,ZHOU H L,et al.Attribute expression of fault-controlled Karst-Fort Worth Basin,TX[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:1522-1527
[11] 杨国权,刘延利,张红文.曲率属性计算方法研究及效果分析[J].地球物理学进展,2015,30(5):2282-2286 YANG G Q,LIU Y L,ZHAGN H W.The calculation method of curvature attributes and its effect analysis[J].Process in Geophysics,2015,30(5):2282-2286
[12] 李福强,贺振华,文晓涛,等.改进的曲率计算方法及其效果分析[J].石油物探,2012,51(2):146-150 LI F Q,HE Z H,WEN X T,et al.An improved curvature calculation algorithm and its effect analysis[J].Geophysical Prospecting for Petroleum,2012,51(2):146-150
[13] KLEIN P,RICHARD L,JAMES H.3D curvature attributes:a new approach for seismic interpretation[J].First Break,2008,26(4):105-112
[14] BUCK D M,ALAM A,TAYLOR J D.Fractured reservoir prediction from 3D seismic volumetric curvature and low frequency imaging[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:422-426
[15] CLAERBOUT J F.Fundamentals of geophysical data processing[M].Palo Alto:McGraw-Hill Book Company,1976:1-269
[16] GAO J H,DONG X,WANG W B,et al.Instantaneous parameters extraction via wavelet transform[J].IEEE Transactions on Geoscience and Remote Sensing,1999,37(2):867-870
[17] 高静怀,吴茜,陈文超,等.小波变换域地震资料瞬时频率分析方法[J].石油物探,2007,46(6):534-540 GAO J H,WU Q,CHEN W C,et al.Instantaneous frequency analysis of seismic data in wavelet transform domain[J].Geophysical Prospecting for Petroleum,2007,46(6):534-540
[18] 高静怀,汪文秉,朱光明.小波变换与信号瞬时特征分析[J].地球物理学报,1997,40(6):821-833 GAO J H,WANG W B,ZHU G M.Wavelet transform and instantaneous attributes analysis[J].Chinese Journal of Geophysics,1997,40(6):821-833
[19] 杨威.曲率属性分析及其应用[D].成都:成都理工大学,2011 YANG W.Analysis of curvature attribute and its application[D].Chengdu:Chengdu University of Technology,2011
[20] 杨威,贺振华,陈学华.结构方位滤波在体曲率属性中的应用[J].石油物探,2011,50(1):27-32 YANG W,HE Z H,CHEN X H.Application of structure-oriented filtering to volumetric curvature calculation[J].Geophysical Prospecting for Petroleum,2011,50(1):27-32
[21] THOMAS G B,FINNEY R L.Calculus and analytical geometry[M].Upper Saddle River:Addison Wesley Publishing Company,1972:1-506
[22] MARFURT K J,KIRLIN R L,FARMER S,et al.3-D seismic attributes using a semblance-based coherency algorithm[J].Geophysics,1998,63(4):1150-1165
[23] WANG X K,CHEN W C,GAO J H,et al.Estimate dip by combining gradient structure tensor and multi-window[J].Expanded Abstracts of 85thAnnual Internat SEG Mtg,2015:1722-1727
[24] WANG X K,YANG C C,CHEN W C,et al.Estimating the dip by constructing gradient structure tensor on instantaneous phase [J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:1580-1584
[25] LUO Y,HIGGS W G,KOWALIK W S.Edge detection and stratigraphic analysis using 3D seismic data[J].Expanded Abstracts of 66thAnnual Internat SEG Mtg,1996:324-327
[26] BARNES A E.Theory of 2-D complex seismic trace analysis[J].Geophysics,1996,61(1):264-272
(编辑:朱文杰)
A 3D curvature attribute analysis method with excellent anti-noise property suitable for high steep formation
WANG Qingzhen,JIANG Xiudi,WENG Bin,DING Jicai,CHEN Jianjun
(CNOOCResearchInstitute,Beijing100028,China)
Curvature attributes is useful in delineating faults,fractures,flexures and folds.However,in order to get curvature attributes,it is necessary to calculate the second-order derivative of seismic data.The derivative calculation process is sensitive to noise and the results are unstable and unreliable.In this paper we present a new 3D curvature attribute analysis method with excellent anti-noise property.Firstly,wavelet transform is used to extract phase-cosine attribute from seismic data.Then apparent dips are calculated based on complex seismic trace theory and filtered using media filter.Finally,many types of curvature attributes with high S/N data are got by combining apparent dips in both directions.Applications of this method to both synthetic and real seismic data show that this method has two advantages.First,it is insensitive to random noise and adapt to low S/N data.Second,it can effectively suppress the pseudo boundary information caused by discontinuity between the tilted strata,so this method is more suitable for steep dipping strata compared with C3 method.
fault detection,curvature,phase cosine,coherence,wavelet transform
2016-03-17;改回日期:2016-10-11。
王清振(1983—),男,硕士,主要从事地震资料解释、属性分析、反演等技术研究及相关软件研发工作。
国家科技重大专项(2016ZX05024-001)资助。
P631
A
1000-1441(2017)04-0559-08
10.3969/j.issn.1000-1441.2017.04.012
This research is financially supported by National Key Project of Science and Technology (2016ZX05024-001).

