利用独立伽马场的反射波时间比例转换波叠前时间偏移
陈 华
(中海石油(中国)有限公司上海分公司,上海200335)
利用独立伽马场的反射波时间比例转换波叠前时间偏移
陈 华
(中海石油(中国)有限公司上海分公司,上海200335)
基于转换波时间比例的转换波叠前时间偏移方法不利于纵波和横波速度分析,也无法保证后续偏移成像的精度。对比分析了转换波和反射波时间比例表征的两种转换波叠前时间偏移方法,指出基于反射波时间比例的转换波叠前时间偏移方法可直接引用由反射波数据求取的纵波速度,将双平方根时间方程的求解简化为单独求取横波速度问题,有效地降低不确定性;在反射波时间比例的表征中引入独立伽马变量,给出利用独立伽马场的转换波叠前时间偏移方法,通过时间匹配求取介质纵横波平均速度比,消除炮检距、地层倾角等因素的影响,在此基础上迭代计算横波速度并更新纵波速度,得到具有明显物理意义的纵波速度、横波速度和介质纵横波平均速度比。实际数据应用表明,该方法具有更高的运算效率和更好的成像效果。
转换波;叠前时间偏移;时间比例;独立伽马
转换波同时包含纵波、横波信息,利用转换波资料能获得地下含流体性质、裂隙及岩石弹性参数等各种信息,在一定程度上弥补纵波勘探的不足。多波多分量地震勘探正在油气勘探开发中发挥着越来越重要的作用[1-3]。
转换波勘探面临两大难题,一是成像,二是转换波与纵波层位对比[4]。由于转换波射线路径不对称,入射波与反射波的速度不同,无法像纵波资料一样在共中心点域(CMP)处理转换波数据,需将其分选到共转换点域(CCP)进行处理。共转换点位置是地层深度、倾角、纵横波速度比和炮检距的函数,要准确求取共转换点位置和道集难度极大,国内外学者为此开展了大量的研究工作。如TESSMER等[5]针对均匀单层模型设定一个恒定的纵横波速度比值,确定共转换点位置,可实现转换波成像,但该方法对中浅层和大偏移距地震数据计算误差较大。李录明等研究出多次迭代逐步逼近的速度分析及抽取CCP道集的方法[6-9]。TSVANKIN等[10]讨论了地震波在各向异性介质中传播的非双曲线时距关系特点,基于泰勒级数展开提出非双曲线走时公式并将其应用于转换波数据成像。LI[11]对TSVANKIN等提出的转换波非双曲时距公式进行改进,给出两个参数的新定义,提高了走时计算的准确性。
迭代速度分析抽道集的方法计算过程复杂而繁琐,成像精度不高。转换波叠前时间偏移技术则能避免共转换点道集的抽取,使转换波归位到真正的反射点上,实现准确的偏移成像[12]。转换波叠前时间偏移可以分为Kirchhoff积分法和波动方程法两类,其中Kirchhoff积分法叠前时间偏移又有共偏移距法、等效偏移距法、虚拟偏移距法等多种类型[13]。马婷[14]、孙珍珠[15]分别利用等效偏移距法和虚拟偏移距法将原始转换波数据映射到共转换散射点道集,使能量按双曲线规律分布,消除了转换波射线路径的不对称性。谢飞等[16]利用TSVANKIN等提出的转换波非双曲时距公式,抽取近似转换点(CACP)道集,从常规速度分析中求取偏移速度参数。
随着各向异性研究的逐渐深入,出现了一系列基于各向异性介质的转换波偏移成像方法[17],包括双平方根旅行时叠前时间偏移、精确旅行时叠前时间偏移、相移加插值法等[18]。马昭军等[19]针对VTI介质在转换波散射旅行时方程中引入3个各向异性参数,在渐近共转换点(ACCP)道集上进行速度分析和偏移。陈海峰等[20]采用指定目的层的共转换点分选方法抽取共转换点道集,通过分步扫描、交互迭代实现VTI介质各向异性速度建模和叠前时间偏移。黄中玉等[21-22]提出一种基于正交各向异性(VTI+HTI)介质的多方位三维转换波叠前时间偏移算法,同时考虑VTI各向异性对转换波中、远偏移距非双曲旅行时计算的影响和高角度垂直裂缝导致的HTI方位各向异性对转换波速度的影响,显著改善了三维转换波叠前时间偏移剖面反射波组的连续性和聚焦性。
各向同性介质转换波叠前时间偏移一般利用转换波或者反射波时间比例进行旅行时表征,其中基于转换波时间比例的方法不便于利用纵波数据进行纵波速度分析。理论上,各向异性介质的转换波叠前时间偏移有更好的精度,但各向异性参数的获取在一定程度上限制了该类方法的广泛应用。本文分析了转换波和反射波时间比例表征的两种转换波叠前时间偏移方法的优缺点,指出基于反射波时间比例的实现方式能更有效地利用纵波数据的信息,给出了利用独立伽马场的转换波叠前时间偏移方法,利用某工区实际资料对方法进行了验证。
1 方法原理
1.1 基于转换波时间比例的积分法叠前时间偏移
转换波射线关系如图1所示,设炮点为(xs,ys),接收点为(xr,yr),成像点为(xc,yc,zc),纵波均方根速度为vP-rms,横波均方根速度为vS-rms。转换波射线时间等于纵波下行时间与横波上行时间之和[23],计算公式如下:
(1)
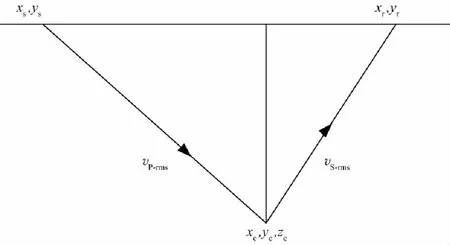
图1 转换波射线关系
设xs=xr=xc,ys=yr=yc,纵波平均速度为vP-ave,横波平均速度为vS-ave,得到零炮检距t0时间:
(2)
定义零炮检距反射纵波双程t0时间为tPP0=2zc/vP-ave,用tPP0作为转换波时深关系方程参数,则有zc=tPP0vP-ave/2。根据公式(1)可得到基于纵波时间比例的转换波传播时间:
(3)
同理,定义零炮检距反射横波双程t0时间为tSS0=2zc/vS-ave,用tSS0作为转换波时深关系方程参数,则有zc=tSS0vS-ave/2。根据公式(1)可得到基于横波时间比例的转换波传播时间:
(4)
转换波t0时间可以定义为纵波双程时与横波双程时的平均,即转换波时间比例可以表示为:
(5)
用转换波t0时间作为转换波时深关系方程参数,则有zc=tPS0(vP-avevS-ave)/(vP-ave+vS-ave)。根据公式(1)可得到基于转换波时间比例的转换波传播时间:
(6)
(6)式即为基于转换波时间比例的叠前时间偏移旅行时解析表达式,其基本实现步骤如下:
1) 根据纵波速度计算地面炮点到地下转换点的射线传播时间;
2) 根据横波速度计算地面检波点到地下转换点的射线传播时间;
3) 计算炮检点射线传播时间之和,并将该时间上的振幅累加到地下转换(成像)点上;
4) 对所有转换波重复积分,得到转换波偏移成像剖面。
转换波偏移的算法原理与反射波偏移基本相同,差别在于传播时间的计算,在接收点一侧采用横波速度。基于转换波时间比例的转换波叠前时间偏移方法计算公式简单且易于实现,但由于采用转换波双程垂直旅行时间比例,不利于进行纵波和横波速度分析,具体表现在速度分析迭代计算过程中难以分辨vP偏大而vS偏小或vP偏小而vS偏大所引起的时间误差,因此无法保证后续偏移成像的精度。
1.2 利用独立伽马场的反射波时间比例转换波积分法叠前时间偏移
在公式(3)中,将参变量γ=vP-ave/vS-ave设为独立变量,则基于反射波时间比例的转换波传播时间为:
(7)
设xs=xr=xc,ys=yr=yc,则公式(7)可以写成:
(8)
(8)式为对应的反射波时间比例。在叠前时间偏移的实现过程中,t0时间通常是固定的,零炮检距时间tPP0随纵横波平均速度比变化而变化。扫描时间tPP0随γ的增大而减小,随γ的减小而增大,当γ接近真值时,扫描时间逼近反射波时间比例。
在地震勘探中,时间属性携带的信息最可靠。用转换波t0时间作为时深关系方程参数,有zc=tPS0·(vP-avevS-ave)/(vP-ave+vS-ave);用反射波双程t0时间tPP0作为时深关系方程参数,则有zc=tPP0vP-ave/2。当二者表示相同的深度时,则有tPS0(vP-avevS-ave)/(vP-ave+vS-ave)=tPP0vP-ave/2。代入介质的纵横波平均速度比γ=vP-ave/vS-ave,得到转换波时间到反射波时间的变换公式,即时间转换比例公式:
(9)
从反射波和转换波剖面上读取地层的时间可以确定伽马值,由于剖面时间代表零炮检距t0时间,因此相当于垂向纵横波平均速度比。真实介质速度难以准确求取,实际求取的速度比总是包含炮检距、地层倾角及上覆地层等各种因素的影响。方程(9)引入的独立伽马变量根据时间关系来求取纵横波平均速度比更可靠,消除了炮检距、地层倾角等因素的影响。
利用独立伽马场的转换波积分法叠前时间偏移实现步骤如下:
1) 引入独立伽马变量,按照时间匹配求取介质纵横波平均速度比;
2) 直接利用反射波数据求出纵波速度vP,以此作为初值,利用转换波数据扫描横波速度vS,得到横波速度vS;
3) 固定横波速度vS,扫描纵波速度vP,更新纵波速度vP;
4) 持续迭代,直至反射波剖面和转换波剖面足够近似,进而得到转换波偏移速度场。
5) 计算纵波时间比例tPP0的转换波传播时间,通过积分法实现转换波偏移成像。
2 实际数据应用效果
将利用独立伽马场的反射波时间比例转换波叠前时间偏移方法应用于某工区实际数据,并与传统基于转换波时间比例表征的转换波叠前时间偏移方法进行了对比。
2.1 基于转换波时间比例的转换波叠前时间偏移
首先在零炮检距剖面上利用时间比例转换公式对转换波时间进行压缩匹配,同时得到反射波叠前时间偏移剖面和转换波叠前时间偏移剖面,如图2,图3所示。可见转换波叠前时间偏移剖面上的大倾角构造与反射波叠前时间偏移剖面明显不符,中深层信噪比偏低,成像效果欠佳。
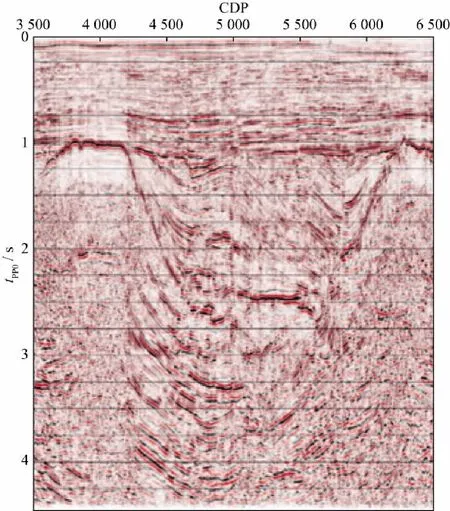
图2 反射波叠前时间偏移剖面

图3 转换波叠前时间偏移剖面
2.2 基于反射波时间比例的转换波积分法叠前时间偏移
采用反射波时间比例tPP0,可直接利用纵波速度进行转换波叠前时间偏移。图4为基于反射波时间比例的横波叠加速度谱,图5为对应的纵波叠加速度谱,从窄幅扫描剖面中可明显观察到扫描时间tPP0随横波速度增大而增大,随纵波速度增大而减小。当纵横波速度逼近真值时,扫描时间趋于真实反射波时间比例。尽管采用纵波速度求取横波速度的过程易于实现,但是对于层状介质,反射波与转换波的纵波速度并不相同,根据转换波拾取的纵波速度可能会略高于根据纵波拾取的纵波速度。究其原因在于,对于转换波而言,激发点一侧的炮检距大于反射波激发点一侧的炮检距,射线在传播过程中更容易穿过高速地层,因此需根据转换波数据对纵波速度进行更新。

图4 反射波时间比例的横波叠加速度谱

图5 反射波时间比例的纵波叠加速度谱
利用基于纵波时间比例拾取的偏移速度,实现基于反射波时间比例的转换波叠前时间偏移,如图6所示。与图3相比,其成像效果更好,深层能量更强。
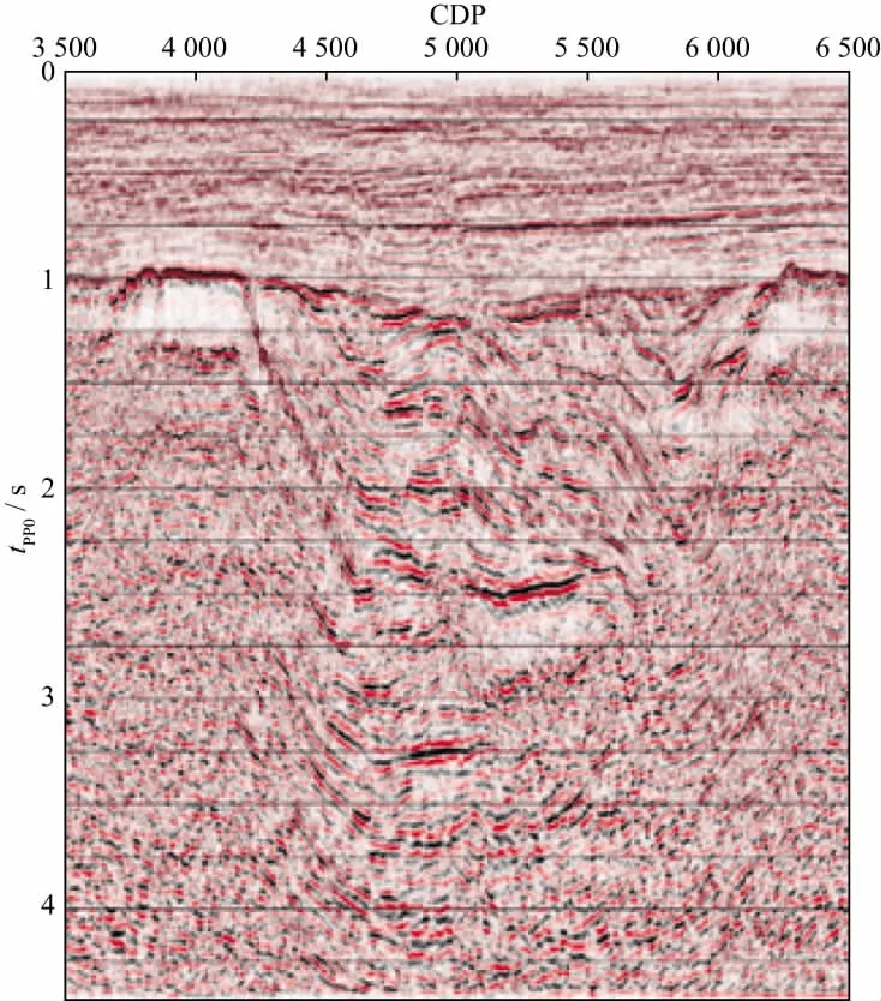
图6 反射波时间比例的转换波叠前时间偏移剖面
说明该方法不仅具有计算公式简单和易于实现的优点,而且能直接引用纵波速度。但是,对于层状介质而言,时间比例中隐含炮检距的影响。理论分析可知,反射波时间比例下的纵横波速度只反映介质特性,而拾取的速度包含炮检距因素,造成的后果是在调整速度使tPP0接近真实反射波时间的时候,该速度未必能将道集上的同相轴拉平,反之亦然。
2.3 利用独立伽马场的反射波时间比例转换波积分法叠前时间偏移
以反射波叠前时间偏移剖面作为参考,利用已知的纵波速度对转换波进行伽马扫描,如图7所示。图7b 是一小段反射纵波成像剖面,图7c是相同位置上的转换波伽马扫描剖面,可见其成像时间随伽马增加而变小,由此可确定伽马值。首次迭代时,横波速度未知,根据纵波初始速度和扫描的伽马确定横波速度,以vS-ave=vP-ave/γ作为初值。伽马取值范围一般在2.0~4.0之间。图8为基于独立伽马场的横波叠加速度谱,图9为基于独立伽马场的纵波叠加速度谱,纵横波速度谱上零炮检距t0时间不再随速度变化而变化,因此能够更准确地求取纵横波速度。与图4,图5基于反射波时间比例拾取的纵横波速度谱相比,基于独立伽马场的速度谱能量团更集中,速度随深度变化的趋势更合理,拾取精度更高,可靠性更强。

图7 反射波时间比例的独立伽马谱a 纵波速度; b 反射纵波参考剖面; c 转换波伽马扫描剖面

图8 基于独立伽马场的反射波时间比例横波叠加速度谱

图9 基于独立伽马场的反射波时间比例纵波叠加速度谱
利用独立伽马场和纵横波速度进行基于反射波时间比例的转换波叠前时间偏移,结果如图10所示。
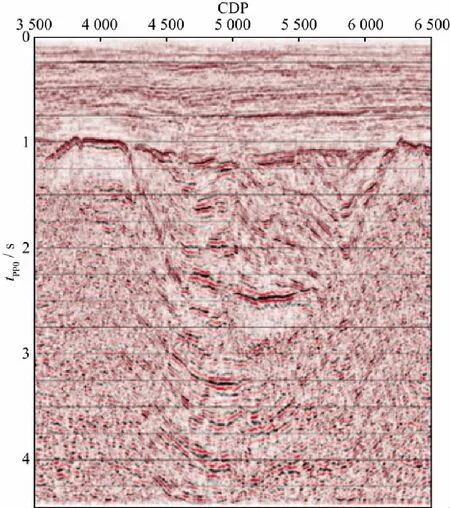
图10 基于独立伽马场的转换波叠前时间偏移剖面
与图6对比可见,引入独立伽马变量后,倾斜地层偏移归位更准确,无论是中浅层还是深层都能准确实现偏移归位,断面清楚,波组特征突出,信噪比和分辨率更高。该方法直接引用纵波速度,优势非常明显,伽马用于时间匹配,速度用于拉平同相轴,二者相互独立,成像效果最佳。
3 结束语
本文提出的反射波时间比例转换波叠前时间偏移算法直接运用由反射波求取的纵波速度,将双平方根时间方程的求解简化为单独求取横波速度,避免了转换波资料处理中的共转换点道集抽取问题;引入独立伽马变量,通过时间匹配求取介质纵横波平均速度比,消除了炮检距、地层倾角等因素的影响,通过转换波伽马扫描和速度分析,迭代更新纵波速度、横波速度和介质纵横波平均速度比,具有更高的运算效率和更好的成像效果。
该方法减少了转换波旅行时方程中未知参数的数量,有效地简化了处理过程;采用反射波时间比例显示转换波偏移成果,符合资料处理人员的视觉习惯,有助于进行效果对比和质量控制。下一步研究工作是开展基于反射波时间比例的转换波叠前时间偏移方法对强各向异性介质和更复杂构造的适应性研究,尤其对具有水平对称轴的横向各向同性(HTI)介质、正交各向异性(VTI+HTI)介质和具有倾斜对称轴的横向各向同性(TTI)介质,该方法的应用效果尚待实际资料的验证。
[1] 程冰洁,徐天吉.转换波资料在川西坳陷储层预测中的应用[J].石油物探,2009,48(2):181-186 CHENG B J,XU T J.Application of converted wave data in reservoir prediction for Chuanxi depression[J].Geophysical Prospecting for Petroleum,2009,48(2):181-186
[2] 付雷,王建民,许红,等.纵波和转换波联合反演技术在松辽盆地北部LMD地区的应用[J].石油物探,2009,48(6):563-567 FU L,WANG J M,XU H,et al.The joint inversion techniques of P-wave and converted wave and applications at LMD zone in the northern of SongLiao Basin[J].Geophysical Prospecting for Petroleum,2009,48(6):563-567
[3] 张明,韩大匡,姚逢昌,等.转换波成像方法综述[J].石油物探,2006,45(5):553-556 ZHANG M,HAN D K,YAO F C,et al.An overview about converted-wave imaging method[J].Geophysical Prospecting for Petroleum,2006,45(5):553-556
[4] 毕丽飞.基于多参数速度模型的转换波叠前时间偏移技术[J].石油地球物理勘探,2010,45(3):337-342 BI L F.The converted wave prestack time migration technique based on multiparameter velocity model[J].Oil Geophysical Prospecting,2010,45(3):337-342
[5] TESSMER G,BEHLE A.Common reflection point data-stacking technique for converted waves[J].Geophysical Prospecting,1988,36(7):671-688
[6] 李录明,罗省贤.多波多分量地震勘探原理及数据处理方法[M].成都:成都科技大学出版社,1997:86-89 LI L M,LUO S X.Principle and data proressing of multi-wave and multi-component seismic exploration[M].Chengdu:Chengdu University of Science and Technology Press,1997:86-89
[7] THOMEN L.Converted-wave reflection seismology over inhomogeneous anisotropic media[J].Geophysics,1999,64(3):678-690
[8] 许士勇,马在田.快速有效的转换波共转换点叠加技术[J].地球物理学报,2002,45(4):557-568 XU S Y,MA Z T.A fast and efficient common conversion point stacking technique for converted waves[J].Chinese Journal of Geophysics,2002,45(4):557-568
[9] 郭向宇,凌云,魏修成.PS转换波共转换点的几种计算方法及实际应用[J].石油物探,2002,41(2):141-143,148 GUO X Y,LING Y,WEI X C.Calculation procedures for common conversion points of PS converted waves and their application[J].Geophysical Prospecting for Petroleum,2002,41(2):141-143,148
[10] TSVANKIN I,THOMSEN L.Nonhyperbolic reflection moveout in anisotropic media[J].Geophysics,1994,59(8):1290-1304
[11] LI X Y.Converted wave moveout analysis revisited:the search for a standard approach[J].Expanded Abstracts 73thAnnual Internat SEG Mtg,2003:805-808
[12] 张丽艳,刘洋,陈小宏.相对振幅保持的转换波叠前时间偏移方法研究[J].石油地球物理勘探,2008,43(2):153-157 ZHANG L Y,LIU Y,CHEN X H.Study on relative amplitude-preserved P-SV converted wave prestack time migration[J].Oil Geophysical Prospecting,2008,43(2):153-157
[13] 张丽艳,刘洋.转换波叠前时间偏移方法综述[J].地球物理学进展,2005,20(4):1134-1139 ZHANG L Y,LIU Y.Overview of prestack time migration for converted wave[J].Progress in Geophysics,2005,20(4):1134-1139
[14] 马婷.转换波叠前时间偏移方法研究[D].西安:长安大学,2011 MA T.Study on converted wave prestack time migration method[D].Xi’an:Chang’an University,2011
[15] 孙珍珠.基于虚拟偏移距的转换波保幅叠前时间成像方法研究[D].西安:长安大学,2014 SUN Z Z.Study of the amplitude-preserving converted-wave prestack time imaging by pseudo-offset migration[D].Xi’an:Chang’an University,2014
[16] 谢飞,常旭,刘伊克.火山岩地震屏蔽层的转换波叠前时间偏移成像[J].地球物理学报,2008,51(6):1899-1908 XIE F,CHANG X,LIU Y K.Converted-wave prestack time migration in volcanic area[J].Chinese Journal of Geophysics,2008,51(6):1899-1908
[17] 蔡晓刚,蔡明刚.弦截迭代法在求取P-S转换波转换点位置和旅行时中的应用——以单一水平界面VTI介质为例[J].石油物探,2012,51(1):79-85 CAI X G,CAI M G.Application of secant iterative method for calculating P-S wave converted-point position and travel time:a case study of VTI medium with single horizontal reflector[J].Geophysical Prospecting for Petroleum,2012,51(1):79-85
[18] 王孝,刘文卿,雍学善,等.三维叠前转换波克希霍夫时间偏移方法研究[J].石油物探,2008,47(2):141-144 WANG X,LIU W Q,YONG X S,et al.The studies of 3-D Kirchhoff PSTM to converted wave data[J].Geophysical Prospecting for Petroleum,2008,47(2):141-144[19] 马昭军,唐建明.叠前时间偏移在三维转换波资料处理中的应用[J].石油物探,2007,46(2):174-180 MA Z J,TANG J M.Application of prestack time migration in 3-D converted-wave data[J].Geophysical Prospecting for Petroleum,2007,46(2):174-180
[20] 陈海峰,李向阳,赵波,等.三维转换波处理技术研究及应用[J].石油物探,2013,52(5):512-518 CHEN H F,LI X Y,ZHAO B,et al.3D converted wave seismic data processing technology and its application[J].Geophysical Prospecting for Petroleum,2013,52(5):512-518
[21] 黄中玉,王于静.一种有效的三维PS波保幅叠前时间偏移方法[J].石油物探,2014,53(4):431-436 HUANG Z Y,WANG Y J.An effective 3D PS-wave true-amplitude prestack time migration method[J].Geophysical Prospecting for Petroleum,2014,53(4):431-436
[22] 黄中玉,余波,王于静,等.正交各向异性介质中多方位三维转换波叠前时间偏移[J].石油物探,2015,54(4):435-442 HUANG Z Y,YU B,WANG Y J,et al.Multi-azimuth 3D converted wave prestack time migration in orthotropic medium[J].Geophysical Prospecting for Petroleum,2015,54(4):435-442
[23] 王有新.应用地震数据处理方法[M].北京:石油工业出版社,2009:54-57 WANG Y X.Application of seismic data processing method[M].Beijing:Petroleum Industry Press,2009:54-57
(编辑:戴春秋)
Prestack time migration for a converted wave based on the independent gamma field
CHEN Hua
(ShanghaiBranch,CNOOCLtd. ,Shanghai200335,China)
Prestack time migration based on a convented wave time scale isn’t suitable for P-wave and S-wave velocity analysis and can’t ensure the imaging accuracy.Prestack time migration for converted wave can be realized according to the converted wave time scale or the reflection time scale.Both methods were compared and analyzed.The method using reflection time scale directly quotes the P-wave velocity obtained from reflection data,and the double square root time formula can be simplified to a separate problem for calculating the S-wave velocity,so as to effectively reduce the uncertainty.We introduce the independent gamma to the course of prestack time migration for a converted wave based on the reflection time scale;the P-wave and S-wave average velocity ratio can be acquired by time matching,accordingly.It can eliminate the effects of the offset,stratigraphic dip and other factors.On this basis,we calculated the S-wave velocity iteratively and updated the P-wave velocity continuously,and the P-wave velocity,S-wave velocity,and P-and S-wave average velocity ratio can be obtained with clear physical meaning.The practical application shows that the method has high computational efficiency and good imaging effect.
converted wave,prestack time migration,time scale,independent gamma
2017-01-05;改回日期:2017-06-02。
陈华(1973—),男,高级工程师,主要研究方向为海洋地震资料采集和处理。
国家科技重大专项(2016ZX05027-002)资助。
P631
A
1000-1441(2017)04-0516-07
10.3969/j.issn.1000-1441.2017.04.007
This research is financially supported by the National Science and Technology Major Project of China (Grant No.2016ZX05027-002).

