一堂意外的研讨课

陈艳霞

以前我们在讲一节课时都是先安排好程序，一节课40分钟，每分钟做什么都有所准备.在这样的课堂上，学生的思维容易受到束缚，不能很好地发挥主观能动性.自主互助课堂实施后，教师的角色发生了变化，不再是课堂的主体，而是成为组织者和引导者，任务是充分调动学生的积极性，开发学生的潜能，帮助学生把知识学好、学透.

相似三角形的判定及性质是初中数学的重点内容，要求学生掌握相似三角形的判定定理及性质，重点是相似三角形的判定及性质的应用，学生不但要能应用、会应用，而且要能灵活地应用.

我在准备“相似三角形的判定及性质的运用”一课时计划讲两个例题，目的是运用判定及性质解决问题.

例1：在△ABC中，过C作直线交AB于P，.（1）∠1满足什么条件时，△ACP ∽△ABC？（2）■满足什么条件时，△ACP ∽△ABC？

分析：（1）因为若使△ACP ∽△ABC，对应点、对应角、对应边已经固定，∠A是公共角，所以只有∠1=∠B时，△ACP∽△ABC.

（2）对应点、对应角、对应边已经固定，∠A是公共角，所以只有夹这个角的两边对应成比例才有△ACP ∽ △ABC，即■=■时，△ACP ∽△ABC.

完成上述例题后，我问学生还有什么疑问，这时有学生提出若使△ACP相似于 △ABC，对应点、对应角、对应边没有固定，但∠A是公共角，应该有两种情况，△ACP ∽△ABC或△ACP∽ △ACB.学生讨论后得出，由于∠1<∠ACB，所以只有∠1=∠B时，△ACP∽△ABC一种情况，其他学生也听明白了.

在这个学生的启发下，问题（2）也可以进行讨论.学生积极讨论，并给出正确的答案：因为 ∠A是公共角，只有夹这个角的两边对应成比例， 才有△ACP相似于△ABC，只有■=■时，△ACP ∽△ABC 一种情况.

我对这个例题进行了变式，如在左图△ABC中，利用几何画板把点C'从C沿CA向上移动， P '从P沿PA向上移动，从而得出第二个例题.

例2：如图，在△ABC中，AB=9，AC=6，AP'=2，C'在AC上，求AC'的值是多少时，△AC'P'与△ABC相似？

学生讨论.过了一会儿，第一小组学生给出答案：AC'=■.第二小组说AC'=3.另一小组又说AC'=■或3.

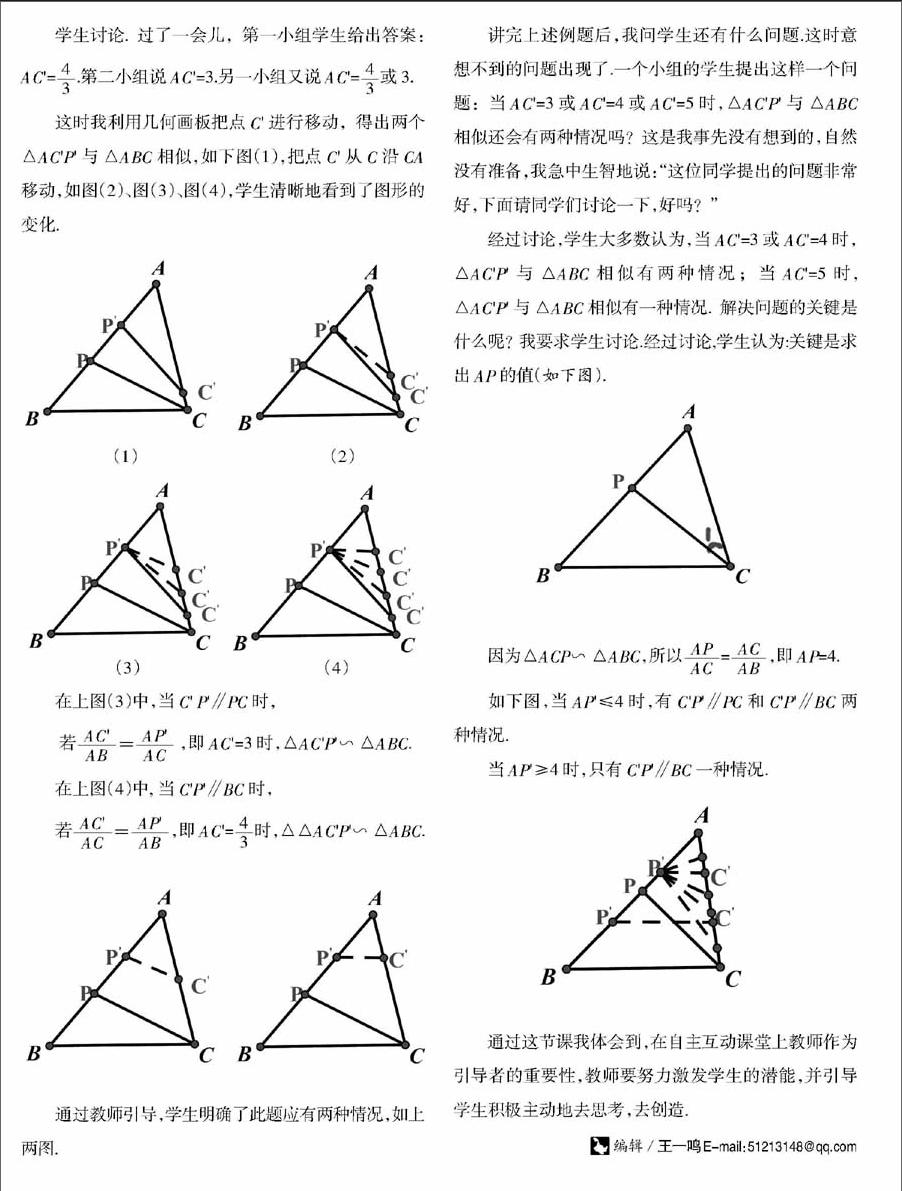
这时我利用几何画板把点C'进行移动，得出两个△AC'P'与 △ABC相似，如下图（1），把點C'从C沿CA移动，如图（2）、图（3）、图（4），学生清晰地看到了图形的变化.

在上图（3）中，当C' P'∥PC时，

若■=■ ，即AC'=3时，△AC'P'∽ △ABC.

在上图（4）中， 当C'P'∥BC时，

若■=■，即AC'=■时，△△AC'P'∽ △ABC.

通过教师引导，学生明确了此题应有两种情况，如上两图.

讲完上述例题后，我问学生还有什么问题.这时意想不到的问题出现了.一个小组的学生提出这样一个问题：当AC'=3或AC'=4或AC'=5时，△AC'P'与 △ABC相似还会有两种情况吗？这是我事先没有想到的，自然没有准备，我急中生智地说：“这位同学提出的问题非常好，下面请同学们讨论一下，好吗？”

经过讨论，学生大多数认为，当AC'=3或AC'=4时，△AC'P'与 △ABC相似有两种情况；当AC'=5时，△AC'P'与 △ABC相似有一种情况.解决问题的关键是什么呢？我要求学生讨论.经过讨论，学生认为：关键是求出AP的值（如下图）.

因为△ACP∽ △ABC，所以■=■，即AP=4.

如下图，当AP'≤4时，有 C'P'∥PC和 C'P'∥BC两种情况.

当AP'≥4时，只有 C'P'∥BC一种情况.

通过这节课我体会到，在自主互动课堂上教师作为引导者的重要性，教师要努力激发学生的潜能，并引导学生积极主动地去思考，去创造.