基于分步式小波神经网络的公交到站时间预测

刘彩云，姚 俭，郑 喆 LIU Caiyun,YAO Jian,ZHENG Zhe

（上海理工大学 管理学院，上海 200093）

基于分步式小波神经网络的公交到站时间预测

刘彩云，姚 俭，郑 喆 LIU Caiyun,YAO Jian,ZHENG Zhe

（上海理工大学 管理学院，上海 200093）

准确的公交到站时间的预测是智能公交系统的关键技术。文章对公交到站时间的影响因素进行分析，提出了基于分步式小波神经网络的公交到站时间预测模型，并通过实例分析对模型进行验证。结论表明，分步式小波神经网络预测模型可有效地进行公交到站时间的预测，预测结果具有较高的准确性和稳定性，较传统预测模型其预测精度提高约34.82%。

交通工程；公交到站时间；小波神经网络；李雅普诺夫指数

0 引言

方便、快捷、安全、高效的公共交通方式是缓解交通问题的主要手段之一[1]。公交线路作为公共交通方式的重要组成部分，对其到站时间的准确预测有利于公共服务信息的传播、公交运行效率的提升以及城市公共交通的发展。

对于公交到站时间的预测，国内外学者建立了多种预测模型。Park[2]、Rahman[3]等调整机器学习的最优参数构建预测模型；Lin[4]等运用历史数据平均分析法建立预测模型并进行多次预测实验；Shalaby[5]等采用Kalman滤波模型利用GPS数据进行公交预测；Meng[6]等分析公交车辆和其他车辆影响因素提出基于概率的公交到站预测模型；王建[7]、罗频捷[8]、季彦婕[9]等分别对神经网络进行改进运算构建公交到站时间预测模型。

然而，以往研究主要以历史数据为研究对象进行自身预测，但对于我国城市交通的复杂状况以及公交运行的随机性，并不能得到较好的预测结果。本文分析公交到站时间的影响因素，构建分步式小波神经网络预测模型，并通过实例分析验证本文模型适用性和有效性。

1 公交到站时间影响因素分析

公交到站时间的影响因素可分为静态因素和动态因素两类。其中，静态因素主要指公交道路的设置，周边的公共设施布局，公交线路的长度等设施条件；动态因素主要指公交调度安排，天气状况、周边交通状况等运行环境条件。由于公交道路建设等静态因素较长时段内变化不明显，对公交到站时间的短时预测影响较小，而动态因素中天气状况、周边交通状况等数据较难获取，因此，本文主要选取历史运行时间、连续班次运行时间及上一路段运行时间为主要影响因素。其中，历史运行时间即为将于预测日前公交线路的历史运行数据；连续班次运行时间则为发车频率较高、班次间隔较短的公交线路选取预测班次前几个班次作为影响因素；上一路段运行时间则为预测班次运行路段前一个路段的交通状况会对此路段的公交运行影响较大，因此作为影响因素分析。对于停靠时间的印象因素，本文主要选取本班次前几个班次同站点的停靠时间为影响因素，并对性质相同的日期同站点的停靠时间作为影响因素分析。

2 模型建立

由影响因素分析可知，公交到站时间预测可主要分为对公交路段运行时间的预测和公交站点的靠站时间的预测[9-10]。本文根据影响因素构建分步式小波神经网络预测模型，前期预测将统计数据输入并进行学习训练，随后进行前期预测。后期预测运用李雅普诺夫指数法以降低由于数据后期混沌运动产生的误差波动，提高预测精度。

2.1 预测步长设定

2.2 前n步预测

（1）设定小波神经网络参数，运用Mexican小波基函数作为神经元函数，并设定隐含层输出值（式（1））和输出层输出值（式（2））。

式中，h（j ）为隐含层中第j节点的输出值；ωij为输入层第i节点和隐含层第j节点间的关联权值；数的时间平移参数，cj为函数的尺寸伸缩参数。

式中，ωjk为隐含层第j节点和输出层第k节点间的关联权值，y（）k为输出层第k节点的输出值。

（2）运用梯度修正法对输出值进行参数修正，并采用Salomon所提出的自适应调节η对神经网络的网络权值和神经元函数参数进行修正并利用初始时间序列）进行网络训练。

（3） 初始时间序列输入到训练完毕的小波神经网络模型中到预测值入到训练完毕的小波神经网络模型中得到预测值按照此方法逐次计算预测值，迭代直至得

到第n步预测值y1（n）为止，则可得到前n步预测值：

（4）将其与修正预测时间序列得到前n步预测时间序列：

2.3 后N-n步预测

（3）计算李雅普诺夫指数：

式中，Δt为样本周期，dt（i）为第i对最邻近点对经过i个离散时间步长的距离。

（4）由李雅普诺夫指数Xt+（m-1）τ+1的预测值为：

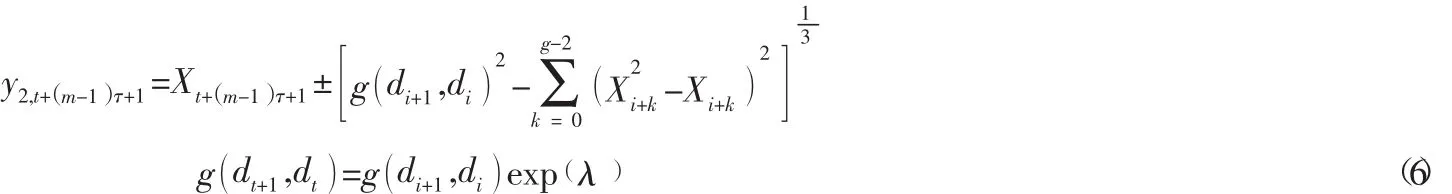
（5）令y2（n+ 1 ）=y2,t+（m-1）τ+1，则得到预测值将y2n+（ ）1与前n步预测时间序列合并，得到预

2.4 最终结果

将前n步预测值y1与后N-n步预测值y2合并，得到最终预测结果：

3 实例分析

3.1 数据来源与参数设定

为验证模型实用性，本文采集上海59路公交2017年4月11日至4月14日的数据作为预测工作日的公交到站时间的原始数据，选取该线路2017年4月15日至4月16日的数据作为预测周末的公交到站时间的原始数据，并选取4月21日和4月23日为测试数据进行实验。

为验证模型精确度和拟合度，本文采用平均绝对误差（MAPE）、均方根误差（RSME）和拟合概率（P）对模型预测值进行评价。

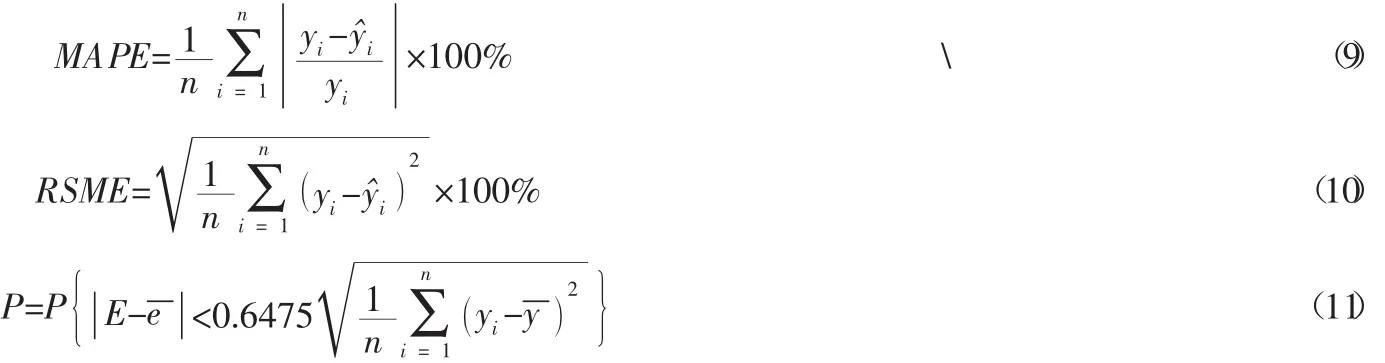
式中，yi为实际值第i个数据；为预测值第i个数据；为数据平均值。

本模型小波神经网络为三层拓扑结构，网络输入层数目为3，中间隐含层节点数目设置为15，网络输出层数目为1，即为输出公交车辆路段运行时间。

3.2 预测结果分析

本文选取传统BP神经网络（NN），小波神经网络（WNN）及本文模型（DWNN）三种模型进行对比分析，并将路段运行时间和停靠时间的预测结果相加，并对总的预测结果进行评价，可得到对比值如表1所示。

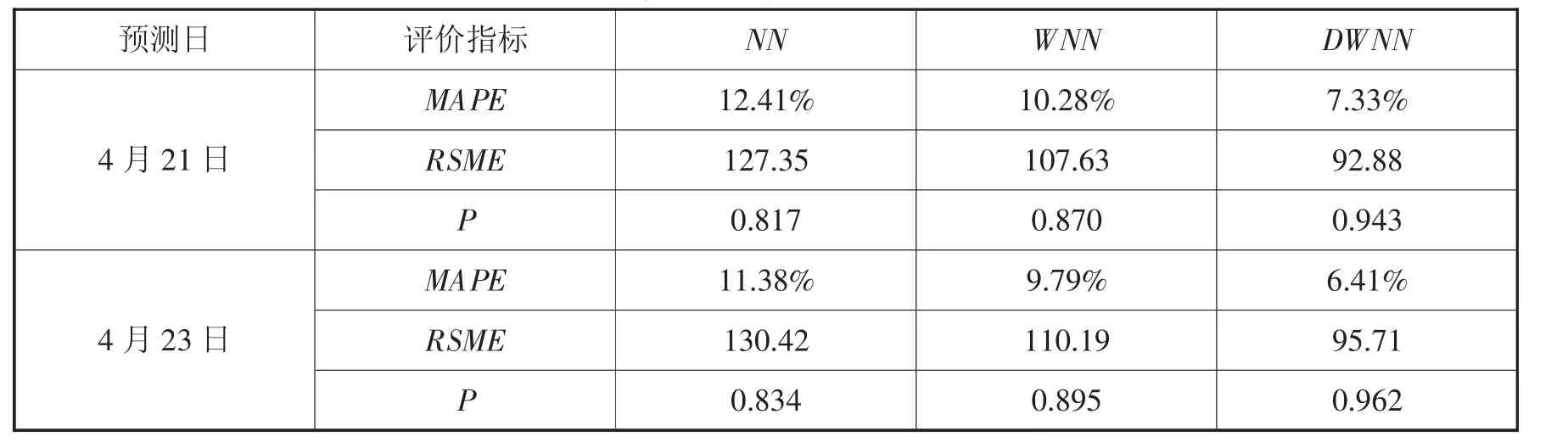
表1 各模型预测值评价指标对比表

由表1可知，与传统预测模型相比，本文模型的预测精度分别提高约40.93%和28.70%。将4月21日的三种模型预测值与实际值进行比较，可得到如图1所示预测对比图及如图2所示误差对比图。

由图1可知，本文模型预测结果稳定性及拟合度均较高，且随机波动性较小。由图2可知，三种预测模型相比，本文模型预测误差较小，误差波动性较小，模型可靠性较高。

图1 4月21日各模型预测值与实际值对比图

图2 4月21日各模型预测误差对比图

4 结 论

通过对公交到站时间的影响因素分析，本文构建了分步式小波神经网络预测模型，并以上海市公交59路为实例分析对模型进行验证评价。评价结果表明，与传统模型相比，本文模型预测结果精确度提高约34.82%，预测误差约为11.89%，误差波动较小，拟合度较高。

[1] 郑喆，韩印，赵靖,等.城市轨道交通与土地价值的关系模型[J].公路交通科技，2017,34(2):113-120.

[2] PARK J,CHEN Z,KILIARIS L,et al.Intelligent vechile power control based on machine learning of optimal control param eters and prediction of road type and traffic congestion[J].IEEE Transactions on Vehicular Technology,2009,58(9):4741 -4756.

[3] RAHMAN H A,MARTI J R.Road traffic forecasting through simulation and live GPS-Feed from inter-vehicle networks[C]// Goble Humanitarian Technology Conference,2012:36-40.

[4] SUN D,LUO H,FU L,et al.Predicting bus arrival time on the basis of global positioning system data[J].Transportation Research Record:Journal of the Transportation Research Board,2007,2034(1):62-72.

[5] VANAJAKSHI L,SUBRAMANIAN S C,SIVANANDANR.Travel time prediction under heterogeneous traffic conditions using global positioning system data from buses[J].IET Intelligent Transport Systems,2009,3(1):1-9.

[6] MENG Q,QU X.Bus dwell time estimation at bus bays:A probabilistic approach[J].Transportation Research Part C:Emerging Technologies,2013,36:61-71.

[7] 王建，邓卫，赵金宝.基于贝叶斯网络多方法组合的短时交通流量预测[J].交通运输系统工程与信息，2011,11(4):147-153.

[8] 罗频捷，温荷，万里.基于遗传算法的模糊神经网络公交到站时间预测模型研究[J].计算机科学，2016,43(6A):87-89,108.

[9] 季彦婕，陆佳炜，陈晓实,等.基于粒子群小波神经网络的公交到站时间预测[J].交通运输系统工程与信息，2016,16(3):60 -66.

[10] 张丽莉，储江伟.公交运行时间预测及仿真[J].计算机仿真,2013,30(7):160-163.

Prediction Model of Bus Arrival Time Based on Distributed Wavelet Neural Network Model

(Management School,University of Shanghai for Science and Technology,Shanghai 200093,China)

Bus arrival time prediction was the key technology of APTS.Based on the influence factor analysis of the bus arrival time,the distributed wavelet neural network model was established to predict the bus arrival time.Finally,the effectiveness of the model was test with the case analysis.Results show that the bus arrival time can be effectively predicted with the distributed wavelet neural network model.The prediction results in weekdays and weekends has high accuracy and stability,improved by about 34.82%compared with the traditional prediction model.

traffic engineering;bus arrival time;wavelet neural network;lyapunov exponent

F570

A

1002-3100(2017)08-0078-04

2017-05-15

上海市一流学科项目，项目编号：S1201YLXK。

刘彩云（1994-），女，辽宁盘锦人，上海理工大学管理学院硕士研究生，研究方向：智能控制、系统工程；姚 俭（1960-），男，上海人，上海理工大学管理学院，教授，博士生导师，研究方向：智能控制、系统工程；郑 喆（1993-），男，黑龙江佳木斯人，上海理工大学管理学院硕士研究生，研究方向：智能控制、系统工程。