一个特殊六阶图H与nK1联图的交叉数
周志东
(衡阳师范学院 数学与统计学院,湖南 衡阳,421002)
一个特殊六阶图H与nK1联图的交叉数
周志东
(衡阳师范学院 数学与统计学院,湖南 衡阳,421002)
图的交叉数是表征一个图的非平面性的一个重要的参数,是拓扑图论中的前沿难题,求解图的交叉数是NP-hard问题。本文确定了一个特殊6阶图H与n个孤立点nK1的联图的交叉数是Z(6,n)+n。
联图;交叉数;nK1;画法
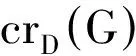

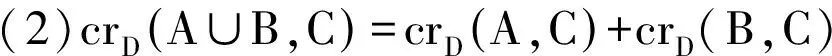
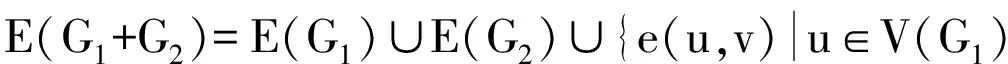

记上式右边表达式为Z(m,n)(这里,对任意实数x,⎣x」表示不超过x的最大整数)。
记6阶图为H,V(nK1)={t1,t2,…,tn},V(nK1)=φ,用Ti(见图1)表示顶点ti与图H的6个顶点之间所连的边集,则有

图1 边集图TiFig.1 Edge set graph Ti
M.Klesc在文献[5]中确定了路Pm,圈Cm以及阶数不超过4的简单图与路,圈的联图的交叉数,在文献[6]中确定了一个6阶图Q与n个孤立点,路Pn以及圈Cn的联图的交叉数。 作者本人在文献[7-11]等文献中确定了一些典型联图的交叉数。本文通过确定了另一个6阶图H(见图2)与n个孤立点nK1的联图的交叉数。

图2 6点图HFig.2 Graph H with 6 vertices

图3 H+nK1的一个好画法Fig.3 A good drawing of H+nK1
1 引理及其证明
引理1:当n=1,2时,cr(H+nK1)=Z(6,n)+n。
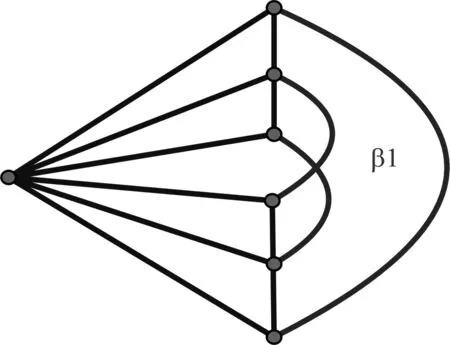
图4 H+K1的一个好画法Fig.4 A good drawing of H+K1
证明 当n=1时,如图4知cr(H+K1)≤1,由图H的特征知其任意一个区域至多含有H的5个顶点,由Jordan曲线定理知把一个顶点ti置于H的任意区域,则Ti与H至少产生一个交叉,所以cr(H+K1)≥1,从而cr(H+K1)=1。
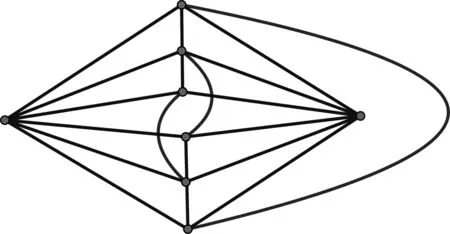
图5 H+K2的一个好画法Fig.5 A good drawing of H+K2
当n=2时,由图5知存在一种好画法使得cr(H+2K1)≤2。事实上H+2K1包含K3,3子图且H+2K1去掉任意一条边e仍包含K3,3子图,若cr(H+2K1)=1,则去掉任意一边e包含K3,3子图,矛盾,所以cr(H+2K1)≥2,因此cr(H+2K1)=2。
引理2:设D是H+nK1的一个好画法,若存在两个Ti,Tj不相交,不妨设为T1,T2,使得crD(T1,T2)=0,则有crD(H,T1∪T2)≥2。
证明 在
2 定理及其证明
定理:cr(H+nK1)=Z(6,n)+n(n≥1)。
证明 由图3知,存在一种好画法φ使得crφ(H+nK1)=Z(6,n)+n,所以cr(H+nK1)≤Z(6,n)+n。下面证明其反向不等式cr(H+nK1)≥Z(6,n)+n,由引理1知,当n=1,2时结论成立。现考虑n≥3,假设cr(H+(n-2)K1)≥Z(6,n-2)+(n-2)成立。
反设存在图H与n个孤立点nK1的联图H+nK1的一个好画法D,使得其交叉数为
crD(H+nK1) (1) 下面我们分如下两种情形来讨论: 情形(1):若存在两个Ti,Tj不相交,不妨设为使Tn,Tn-1使得crD(Tn,Tn-1)=0(n≥2),因为Tn∪Tn-1∪Tk同构于K3,6,而cr(K3,6)=6,所以crD(Tn∪Tn-1,Ti)≥6。又因为H∪(T1∪T2∪…∪Tn-2)同构于H+(n-2)K1,所以有 crD(H+nK1)=crD(Tn∪Tn-1∪H∪(T1∪T2∪…∪Tn-2))≥ 6(n-2)+2+Z(6,n-2)+(n-2)≥ Z(6,n)+n, 与(1)矛盾,所以crD(Ti,Tj)≠0。 情形(2):由情形(1)知因而存在两个Ti,Tj相交crD(Ti,Tj)≥1(1≤i≠j≤n),由 crD(H+nK1)=crD(K6,n)+crD(H)+crD(K6,n,H)≥Z(6,n)+crD(H)+crD(K6,n,H) 联合(1)有 crD(H)+crD(K6,n,H) (2) 所以至少存在某个Ti,不妨设为Tn使得crD(Tn,H)=0。此时crD(H)(或crD(H∪Tn)=1)。下面分以下两种子情形来讨论: 子情形(1):当 crD(H+nK1)=crD(K6,n-1)+crD(H∪Tn)+ crD(K6,n-1,H∪Tn)≥ Z(6,n-1)+1+4(n-1)≥Z(6,n)+n。 与(1)式矛盾。 子情形(2):由图H的结构特征知 crD(H+nK1)≥crD(K6,n-1)+crD(H∪Tn)+ crD(K6,n-1,H∪Tn)≥ Z(6,n-1)+1+3x+5(n-x-1)= Z(6,n-1)+1+5(n-1)-2x 由(2)式知2x crD(H+nK1)≥crD(K6,n-1)+crD(H∪Tn)+ crD(K6,n-1,H∪Tn)≥ Z(6,n-1)+1+5(n-1)-2x≥ Z(6,n-1)+1+5(n-1)-(n-1)≥ Z(6,n)+n。(n≥1) 与(1)式矛盾。 综上所述,反设(1)式不成立,因而有crD(H+nK1)≥Z(6,n)+n.结合cr(H+nK1)≤Z(6,n)+n,所以有cr(H+nK1)=Z(6,n)+n(n≥1)成立。从而完成了定理的证明。 [1]BONDY J A,Murty U S R.Graph Theory With Applications[M].Published in Great Britain:The Macmillan Press Ltd.,1976. [2]周志东,黄元秋,彭小多,等.一个小图与路和圈的联图的交叉数[J].系统科学与数学,2013,33(2):206-216. [3]GAREY M R,JOHNSON D S.Crossing number is NP-complete[J].SIAM Journal on Algebraic Discrete Methods,1993,4:312-316. [4]WOODALL D R.Cyclic-order graphs an Zarankiewicz's crossing number conjecture[J].Journal of Graph Theory,1993,17(6):657-671. [5]KLESC M.The join of graphs and crossing numbers[J].Electronic Notes in Discrete Mathematics ,2007,28:349-355. [6]KLESC M.The crossing numbers of join of the special graph on six vertices with path and cycle[J].Discrete Mathematics,2010,310:1475-1481. [7]周志东,王晶.W6 × Sn的交叉数[J].运筹学学报,2013,17(2):1-9. [8]周志东,吕胜祥.关于一个特殊六阶图与路和圈的联图的交叉数[J].数学进展,2014,43(1):69-80. [9]ZHOU Zhidong,HUANG Yuanqiu,WANG Jing.On the Crossing Numbers of the Joint Graphs of a Path or a Cycle,ARS Combinatoria.(SCI,已录用). [10]周志东,李龙.一个特殊六点图Q与 ,nK1,Pn及Cn的交叉数[J].运筹学学报,2016,20(4):115-126. [11]周志东,李龙.一个6点图与路的联图的交叉数[J].应用数学,2017,30(1):72-77. On the crossing number of the joint graph of six order graphHandnK1 ZHOU Zhidong (Department of Mathematics and Computational Science,Hengyang Normal University,Hengyang 421002,China) The crossing number problem is in the forefront of topological graph theory.It is a vital subject in topological graph theory.In the paper,for the special graphHwith six vertices,we prove that the crossing numbers of its join with n isolated verticesnK1areZ(6,n)+n. joint graph;crossing number;nK1; drawing 1672-7010(2017)04-0007-04 2017-05-26 湖南省教育厅优秀青年基金项目(17B040);湖南省“十三五”重点建设学科项目资助 周志东(1980-),男,湖南邵阳人,讲师,博士,从事图论及其应用研究;E-mail:zzdongwww@163.com O157.5 A

