石墨烯双曲超材料光学特性的研究进展

谭朝幻+王昊月+孟方俊+王胜明+许吉

摘 要：双曲超材料因其所拥有的奇异特性具有非常大的应用前景，其中金属材料构成的双曲超材料是近年来的一个研究热点，而用石墨烯代替金属构成的石墨烯-电介质超材料可以通过对入射电磁波频率和化学势的调节来实现双曲色散特性，其相比于金属-电介质双曲超材料和金属纳米线双曲超材料，具有更小的传输损耗、更小的结构体积并且更易于光电集成。该文对石墨烯-电介质双曲超材料在可见光、红外以及太赫兹等几个波段的光学特性学术工作展开调研，首先介绍石墨烯和双曲超材料的相关基础知识，进而针对石墨烯双曲超材料的介电常数、磁导率和折射率几个方面的调控机制来实现对光子行为的调控目的进行阐述，并介绍了相关应用。

关键词：石墨烯 双曲超材料 光学特性

中图分类号：TQ127.11 文献标识码：A 文章编号：1672-3791（2017）07（b）-0001-04

1 双曲超材料及石墨烯简介

超材料是一种人工微结构材料，是由亚波长尺度的结构单元构建的一种特殊结构，通过对结构单元的材料和厚度的调节来达到控制电磁波传输的目的，从而可以实现自然界中的材料所不具有的特性。具有双曲色散关系的双曲超材料（Hyperbolic Metamaterials， HMMs）是超材料中的一种，也称为不确定介电媒质（Indefinite permittivity media，IPMs），该媒质的的电磁特性可以通过介电常数张量及磁导率张量来进行描述。由于双曲超材料所具有的独特的双曲色散关系，使其表现出一系列新的光学现象，在隐身、光波导、成像、超透镜、聚焦、热传输、和负折射等方面具有潜在的实用价值。

1.1 双曲超材料

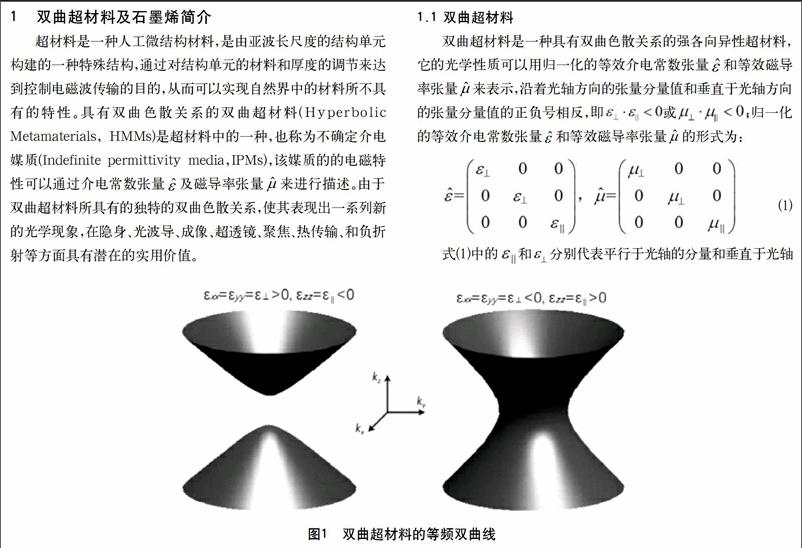
双曲超材料是一种具有双曲色散关系的强各向异性超材料，它的光学性质可以用归一化的等效介电常数张量和等效磁导率张量来表示，沿着光轴方向的张量分量值和垂直于光轴方向的张量分量值的正负号相反，即或；归一化的等效介电常数张量和等效磁导率张量的形式为：

式（1）中的和分别代表平行于光轴的分量和垂直于光轴的分量。当磁导率μ=1时，介电常数是各向异性的，此时当入射电磁波为TM偏振态时，双曲超材料如图1所示。

当入射光频率小于金属的等离子体频率时，金属中的自由电子的极化响应是与电场方向相反的，所以金属介电常数的实部为负值。只需要使其一个或两个主轴方向的介电常数张量为负值，便可实现材料的双曲色散关系。目前双曲超材料的构成方式主要有两种：一种是由金属-电介质交替排列的多层膜结构，通过调整金属的种类和占空比来实现双曲色散关系；另一种是将金属纳米线镶嵌在电介质中，通过对纳米线半径大小的调节和排列方式的设计来实现双曲色散关系。金屬-电介质多层膜结构相比于纳米线阵列结构更简单，更易于制备，在中红外和THz波段可以利用石墨烯与电介质的交替排列组成双曲超材料。用石墨烯代替金属构成的石墨烯-电介质超材料可以通过对入射电磁波频率和化学势的调节来实现双曲色散特性，其相比于金属-电介质双曲超材料和金属纳米线双曲超材料具有更小的传输损耗、更小的结构体积并且更易于光电集成。该文主要讨论的是多层膜结构双曲超材料。

1.2 石墨烯的光学参数

石墨烯的参数主要由其面电导率来表征，石墨烯中的载流子密度和费米能级可以通过栅极电压即静电掺杂来控制，因此石墨烯的相关光学性质是由加在石墨烯上的栅极电压所决定的。有关石墨烯电导率的计算可以用随机相位近似法（RPA）来表征[1]：

.

其中为玻尔兹曼常量；为室温；为弛豫时间；为费米能级，其取决于石墨烯电荷载流子浓度。在我们的计算中，载体弛豫时间是经过实验中使用的石墨烯样品的传输测量来估计的。方程的第一项是内部变换，第二项称为带间转换[2]。石墨烯等效介电常数的公式为：

其中为石墨烯电导率；为电介质的厚度， 是石墨烯的占空比，其中是石墨烯的厚度。则等效介电常数的垂直分量公式为：

等效介电常数的水平分量公式为：

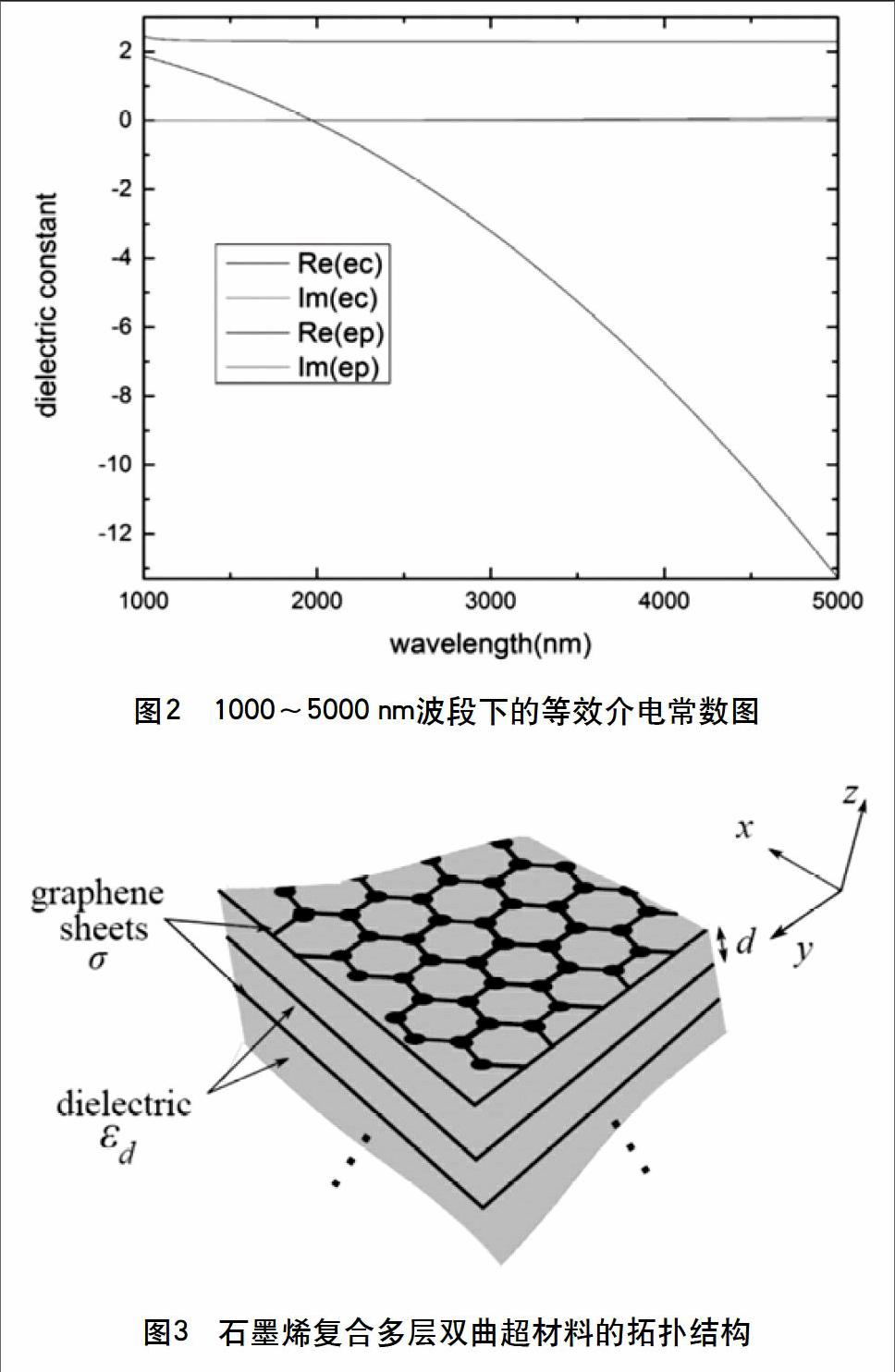
其中，石墨烯厚度，为室温300 K，介质层二氧化硅的介电常数，化学势=0.9 eV，取周期数，运用Matlab软件编程计算得到等效介电常数。与虚部都较小可以忽略，在大于2 000 nm 左右的波长范围内，实现了。

图2中1 000～5000 nm波段下的等效介电常数（其中ec为等效介电常数的垂直分量；ep为等效介电常数的水平分量）

2 石墨烯双曲超材料研究新进展

2.1 石墨烯双曲超材料的宽波段可调性

2013年Mohamed A. K. Othman等人介绍了一种如图3所示的石墨烯复合多层结构 [3]，即石墨烯-电介质多层膜结构，该结构在太赫兹和中红外频率处呈现双曲型色散关系。他们使用简单的均质方案计算出了多层的有效介电常数张量。此外，还采用布洛赫理论分析了双曲超材料内的传播模式的色散关系，并证明了均匀化方案在所讨论的宽频带中与布洛赫理论的一致性。

同年，Mohamed A. K. Othman等人又在远红外频率和中红外频率下引入了可调石墨烯HMMs。与自由空间相比，HMMs表现出的等频双曲色散性质允许波在广泛的空间频谱中传播，使本征局域态密度大幅度提高，这可以应用于近场的超吸收和对分子辐射衰变率的精确控制[4]。由此，他们所提出的HMMs在太赫兹和红外区域中可以实现由石墨烯的化学势有效地控制的可调谐应用。

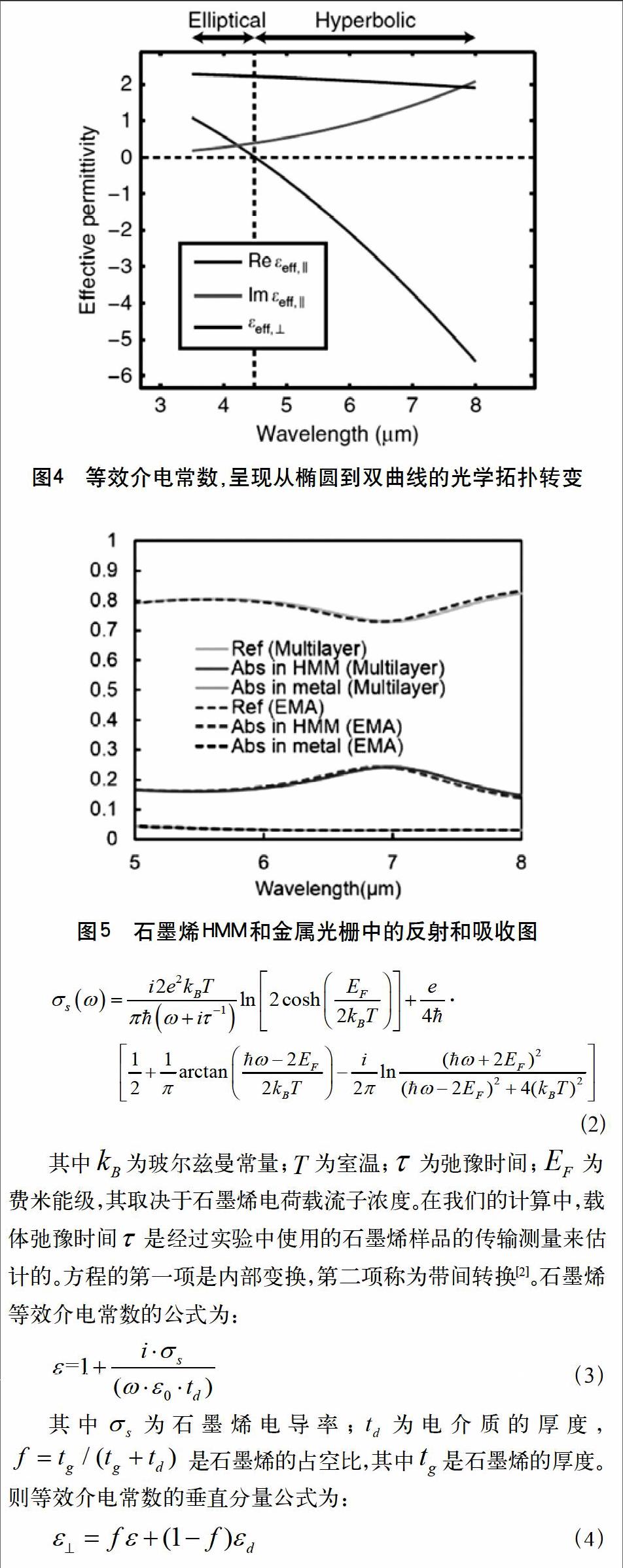
2015年，Chang Y. C.等人通过实验研究了石墨烯和Al2O3层的多层交替结构[5]。他们采用了化学气相沉积法得到石墨烯，通过掺杂的方法来提高层电导率，结果表明，这种掺杂的化学气相沉积的石墨烯在中红外范围内的确具有良好的光学性能。其色散关系在波长为4.5μm处发生了从椭圆到双曲线的光学拓扑转变如图4所示，这与这与K. V. Sreekanth等人描述的临界频率的情况相符。

2.2 石墨烯双曲超材料实现负折射

2013年，K. V. Sreekanth等对石墨烯双曲超材料在太赫兹波段的负折射现象进行了数值研究[6]，发现石墨烯双曲超材料的双曲色散关系可以通过调整化学势和电介质层的厚度而改变，而在波长改变时，其色散关系会从椭圆向双曲分布转变。这种转变存在一临界频率，他们在远低于这个临界频率的斜入射情况下观察到了正、负相位的折射率。并且在负折射区域内，还观察到高度限制的大量等离激元模式，这进一步证明了石墨烯双曲超材料存在负折射现象。石墨烯双曲超材料可能应用在超透镜的设计上，使其具有更小的损耗、突破更高的衍射极限、实现更精细的光场调控。

2.3 石墨烯双曲超材料實现超吸收

2013年Mohamed A. K. Othman等人在远红外频段对石墨烯双曲超材料进行了研究[7]。他们使用石墨烯表面电导率模型，将石墨烯片作为具有复杂导纳的集体层来处理，得到了多层结构的均化公式，并用传输矩阵法比较来研究均化的结构和极限。通过静电偏置改变石墨烯层的化学势来实现反射和透射性的可调，并提出用石墨烯双曲超材料作为表面近场的超级吸媒质。

2015年，Chang Y. C.等人进行数值仿真，设法用金属光栅将光从自由空间耦合到石墨烯HMMs中[8]。结果表明，光可以有效地耦合到HMM板中的高k导模中，并被石墨烯层吸收，这一发现可以有效应用于超薄超吸收体的发明研究中。

图5图中分别为石墨烯HMM和金属光栅中的反射和吸收，其中实线代表12个周期的石墨烯-电介质HMMs，虚线代表等效介质近似的多层均匀介质[8]。

2.4 石墨烯双曲超材料实现的其他光子调控效应

在光开关、存储器件和量子光学等领域，慢光一直是热点课题。2014年，Sayem A. A.等人从理论上提出了基于石墨烯双曲超材料的太赫兹波段的可调慢光器件[9]。利用石墨烯的可调性，他们所提出的器件也是可调的，为石墨烯双曲超材料在光子开关、光学缓冲器和存储设备等方面的应用提供了一个新的方向。

2015年，陈拓等人研究了基于石墨烯的一些光子学器件，包括太赫兹的宽带吸波器、圆偏振的分光器以及磁光克尔效应增强器件等[10]。他们提出了一种由石墨烯-介质层堆栈而成的类金字塔结太赫兹吸波材料，这种亚波长周期结构的器件能够对不同的圆偏振光进行有效的控制。

2014年Yuanjiang Xiang等人提出了一种在近红外频率波段对石墨烯双曲超材料和各向同性介质之间的布洛赫表面波进行了研究[11]。通过静电偏置，表面布洛赫波存在的频率和频率范围可由石墨烯片层的不同费米能级来实现调节。通过减小石墨烯-电介质层状结构中的电介质的厚度或增加石墨烯片的层数，表面布洛赫波存在的频率范围可以扩大。在近红外和可见光波段计算了亚波长极限内入射光的偏振态s和p极化的石墨烯-电介质层结构的色散关系。

图6中（a）（b）（c）分别为费米能级，电介质的厚度和石墨烯层数对实部的影响；其中灰色曲线在（a）（b）（c）中分别代表、，、 eV， nm、 eV时自由空间中的光波[11]。

3 结语

目前关于石墨烯-电介质双曲超材料的研究多是集中在中红外到太赫兹波段的电磁波的传输行为，如通过对化学势的调节可能出现负折射或正折射现象，对于可见光波段以及近红外波段的光学特性的研究较少，石墨烯双曲超材料在器件等方面的潜在应用还未被研究，这些都值得我们更加深入全面的探索。石墨烯双曲超材料是一个种新兴的材料，其特殊的光电特性可以解决传统材料和技术所不能解决的问题， 相信在不久的将来，我们就能看到石墨烯双曲超材料实际应用于生产生活中， 实现从技术向产业的跨越。

参考文献

[1] Yao Y，Kats M A，Genevet P，et al.Broad electrical tuning of graphene-loaded plasmonic antennas[J].Nano Letters，2013，13（3）：1257.

[2] Ferrari L，Wu C，Lepage D，et al.Hyperbolic metamaterials and their applications[J].Progress in Quantum Electronics，2015（40）：1-40.

[3] Othman M A K，Guclu C，Capolino F.Graphene-based hyperbolic metamaterial[A].IEEE International Symposium on Antennas and Propagation & Usnc/ursi National Radio Science Meeting.IEEE[C].2013：484-485.

[4] Othman M A K，Guclu C，Capolino F.Graphene-based Hyperbolic Metamaterial at Terahertz Frequencies[Z].OSA，2013.

[5] Chang Y C，Liu C H，Liu C H，et al.Realization of mid-infrared graphene hyperbolic metamaterials[J].Nature Communications，2016（7）：10568.

[6] Sreekanth K V，De Luca A，Strangi G.Negative refraction in graphene-based hyperbolic metamaterials[J].Applied Physics Letters，2013，103（2）：509.

[7] Othman M A，Guclu C，Capolino F.Graphene-based tunable hyperbolic metamaterials and enhanced near-field absorption.[J].Optics Express，2013，21（6）：7614-7632.

[8] Chang Y C，Liu C H，Liu C H，et al.Mid-infrared hyperbolic metamaterial based on graphene-dielectric multilayers[A].Lasers and Electro-Optics. IEEE[C].2015：1-2.

[9] Sayem A A， Mahdy M R C，Hasan D N，et al. Tunable slow light with graphene based hyperbolic metamaterial[A].Icece[C].2014：230-233.

[10] 陈拓.基于石墨烯的光子学器件的研究[D].浙江大学，2015.

[11] Xiang Y，Guo J，Dai X，et al.Engineered surface Bloch waves in graphene-based hyperbolic metamaterials[J].Optics Express，2014，22（3）：3054.