环锭细纱机卷绕成形纱长不同计算方法的比较和应用

韦金平

(经纬纺织机械股份有限公司 榆次分公司，山西 晋中 030601)

环锭细纱机卷绕成形纱长不同计算方法的比较和应用

韦金平

(经纬纺织机械股份有限公司 榆次分公司，山西 晋中 030601)

为了精确计算环锭细纱机钢领板每次升降卷绕纱线的精确长度，以FA506型环锭细纱机传动结构为基础，分析对比在机械升降方式和电子升降方式下，近似算法和精确算法产生的绕纱长度差异，并探讨钢领板上升速度和前罗拉出纱速度与卷绕转角的关系。指出：近似纱长总大于精确纱长，且卷绕齿轮副ZF/ZG的近似值总比精确计算的小，不利于成形和高速络筒，故电子升降应采用精确算法；通过分析钢领板在上升状态时的瞬时速度和卷绕转角的关系式，可计算伺服电机的瞬时转速。

环锭纺；卷绕成形；机械升降；电子升降；纱长；近似计算；精确计算

0 引言

随着环锭细纱机和络筒机速度的不断提高，为防止毛羽、断头、脱圈等指标恶化，对细纱机管纱成形质量及其卷绕成形控制精度提出更高的要求。传统机械升降式卷绕成形控制方式是有级的，其控制采用近似算法。当钢领板改进为电子升降式控制时，伺服电机可直接控制钢领板的升降速度，做到无级、准确，其控制应采用精确算法。电机控制使根据纱线实际卷绕情况，重新精确计算钢领板升降速度变得具有可操作性，也使管纱成形状态更加理想。

环锭细纱机管纱卷绕成形过程是钢领板在“上多下少”的往复运动中，细纱层层卷绕，在凸钉作用下完成管底纱后，以绕锥形等螺距螺旋线的方式，完成中纱和大纱的成形。若不考虑捻缩的影响，单位时间内前罗拉的出纱长度应等于纱管的绕纱长度[1]。下文以FA506型细纱机最新传动结构为例，分析环锭细纱机采用精确算法与近似算法的区别。

1 机械升降控制的近似算法

设ZF/ZG为卷绕齿轮副，前罗拉的直径为DF，成形凸轮带动钢领板上升和下降的速度比为1∶k。成形凸轮每转动一周，钢领板完成一个升降短动程，根据FA506型细纱机的传动结构可得，此过程前罗拉出纱长度L为：

(1)

钢领板单次短动程纱管的绕纱长度采用近似算法，如图1所示。

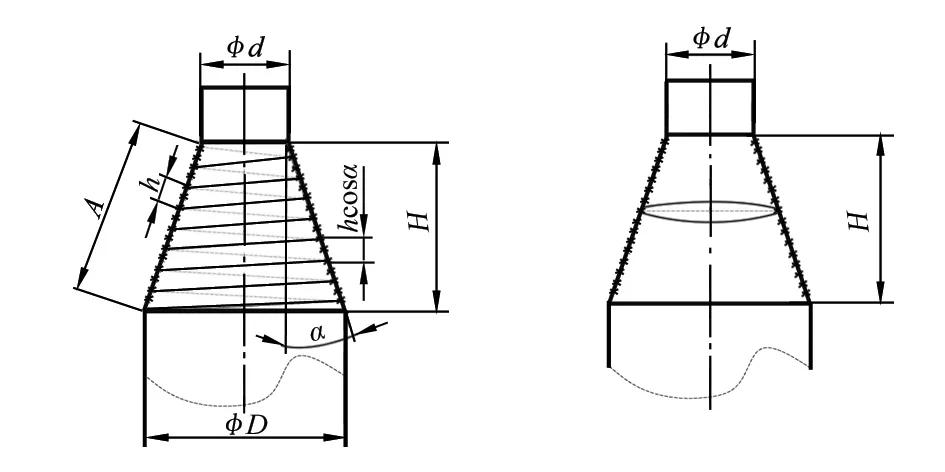
图1 细纱短动程纱管绕纱长度近似计算示意

图1中d为筒管直径，D为成纱直径，H为短动程高度，h为圈距，A为短动程圈距和，α为成形角(半锥角)，法向螺距为hcosα，圆锥螺旋线每圈的运动轨迹可近似地看作一个圆，再近似到锥台的中径圆求周长L′如下：

(2)

式中，1/k为降程倍数，由L=L′可推知卷绕齿轮副的理论齿数比如下：

(3)

近似算法使计算绕纱长度与实际绕纱长度间存在一定的误差，进一步影响卷绕齿轮副ZF/ZG，而齿轮在设计时还需要考虑模数标准化等因素，导致ZF/ZG值需再次调整，这对于机械升降的有级和模糊而言，近似计算法是可以被接受的，也是一种经济实用的计算方法[2]。

2 电子升降控制的精确算法

当机械升降方式变为由伺服电机控制的电子升降方式时，无需升降凸轮和ZF/ZG工艺齿轮，即可实现对钢领板的无级调速。理论上，可根据细纱实际卷绕情况实现精确计算，以消除近似计算产生的误差，使管纱实际成形更接近于理论形状。

在钢领板上升过程中，纱线的卷绕过程精确计算数学模型如图2所示。圆锥位于空间直角坐标系xyz中,设d为筒管直径，D为管纱直径，α为卷绕角(半锥角)，设M′点从x轴开始向上绕圆锥面做法向螺距为hcosα的螺旋运动，求M′点轨迹弧长与M′点的转角θ的关系。

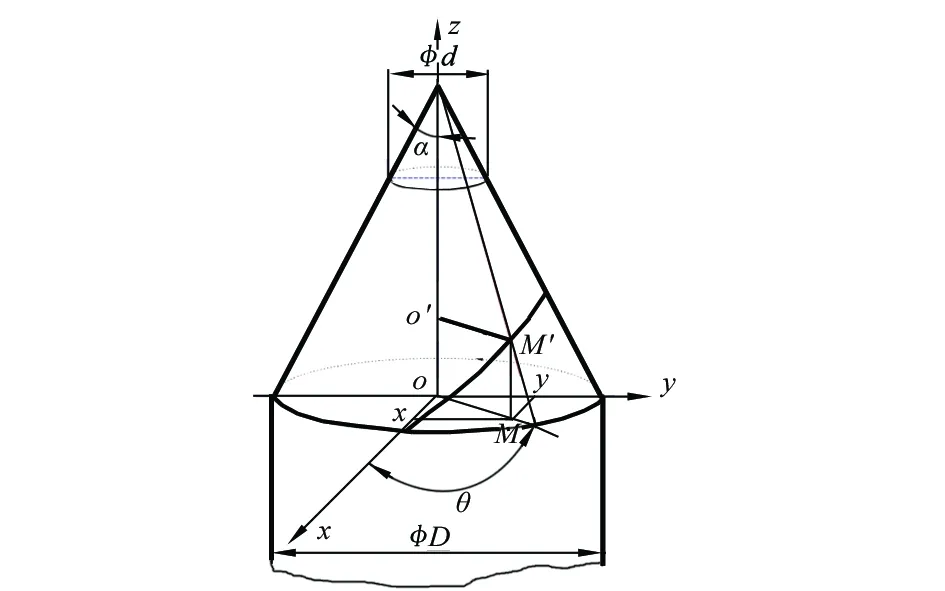
图2 细纱绕纱长度精确计算数学模型

由2π/(hcosα)=θ/oo′,得oo′=MM′=z=h×cosα×θ/(2π)，进而得：

(4)

M′在x轴的投影长度为：

(5)

M′在y轴的投影长度为：

(6)

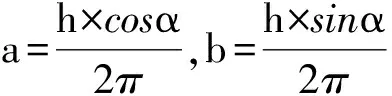
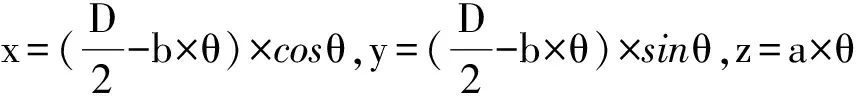
(7)

(8)

dz=adθ

(9)

微分弧长：

(10)

由不定积分公式：

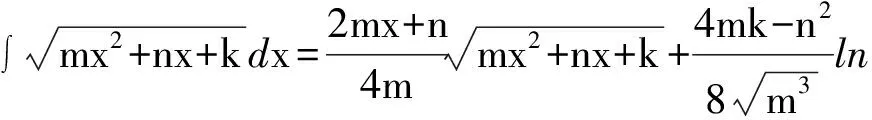
(11)

得:

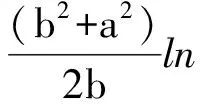
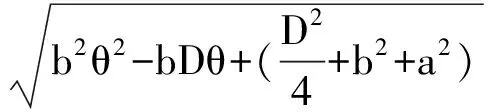
(12)

还原后得：

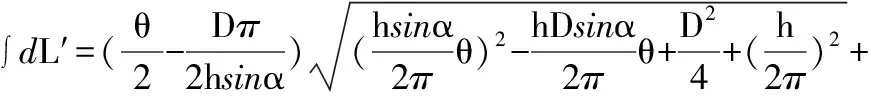
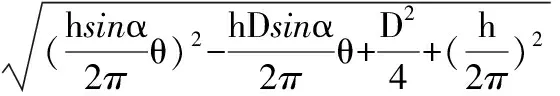
(13)

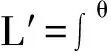
3 两种算法比较

表1 近似算法与精确算法的比较

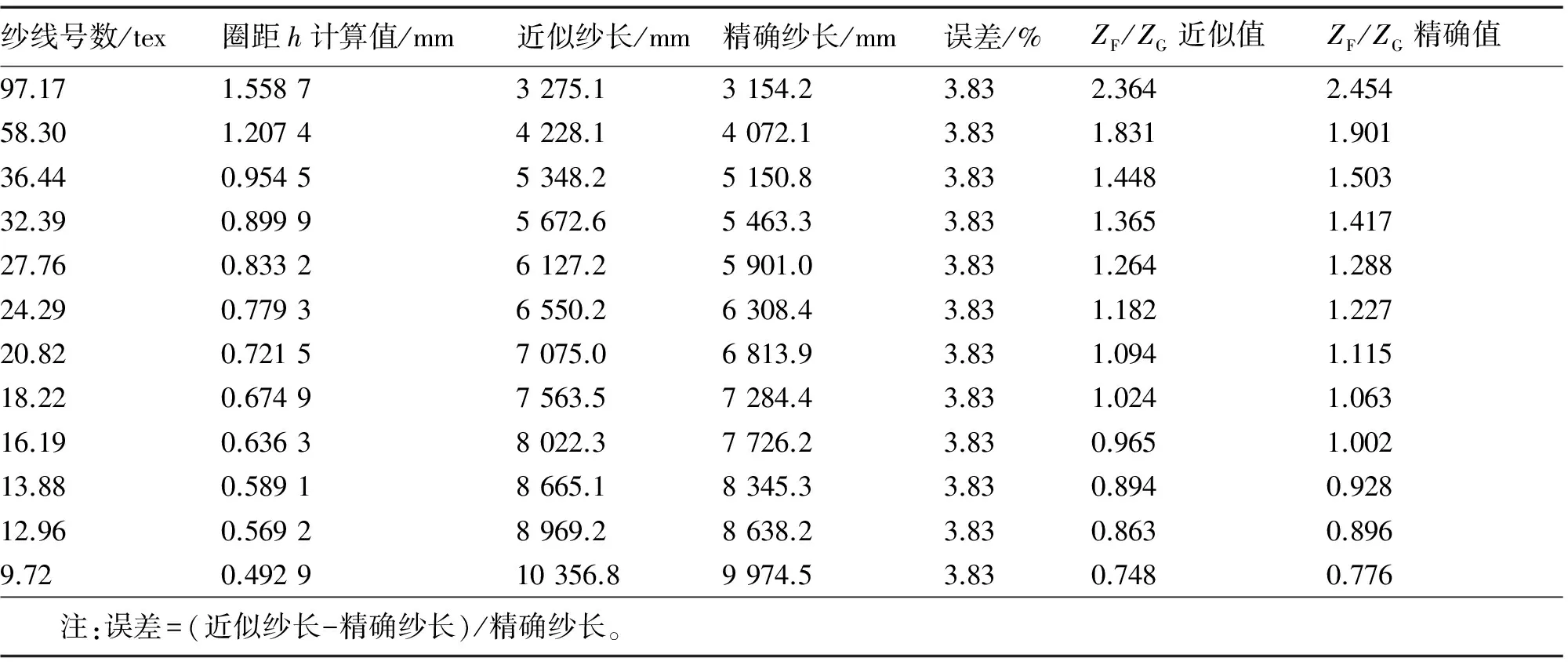
纱线号数/tex圈距h计算值/mm近似纱长/mm精确纱长/mm误差/%ZF/ZG近似值ZF/ZG精确值97．171．55873275．13154．23．832．3642．45458．301．20744228．14072．13．831．8311．90136．440．95455348．25150．83．831．4481．50332．390．89995672．65463．33．831．3651．41727．760．83326127．25901．03．831．2641．28824．290．77936550．26308．43．831．1821．22720．820．72157075．06813．93．831．0941．11518．220．67497563．57284．43．831．0241．06316．190．63638022．37726．23．830．9651．00213．880．58918665．18345．33．830．8940．92812．960．56928969．28638．23．830．8630．8969．720．492910356．89974．53．830．7480．776 注：误差=(近似纱长-精确纱长)/精确纱长。

由表1可看出，近似算法计算出的纱长总是大于精确纱长，两者间存在3.83%误差。通过进一步计算可知，当卷绕角为11.669°，卷绕直径为32 mm，纱管直径为13 mm，其它参数不变时，其误差高达4.26%。这是由于ZF/ZG近似算法比精确计算的值小，而ZF/ZG偏小会导致实际圈距偏小，不利于实际成形和高速络筒，因此，电子升降应采用精确算法[4]。

4 电子升降中钢领板速度的控制

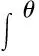
在钢领板上升时，单位时间内细纱的卷绕长度，即卷绕速度vj：

(14)

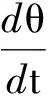
(15)

所以卷绕速度vj：

2π(vd-vt)=v1

(16)

其中，v1为前罗拉出纱速度，此处不计捻缩系数。又因dz=adθ，所以钢领板上升速度：

(17)

代入原数据得：

(18)

式(18)表明了钢领板上升速度和前罗拉出纱速度与卷绕转角θ的关系。

需要说明的是，在电子升降中，因为上升螺距和下降螺距不同、卷绕方式不同(从下到上或从上到下)、数学模型的坐标系建立位置不同，使下降过程中的dL′的公式略有不同，钢领板的升降过程在控制程序里应该分开控制。下降过程速度计算公式在理论上和上升过程一样[5]，不再赘述。

5 结论

5.1 通过分析环锭纺卷绕的实际状态，给出卷绕长度精确计算公式，以11.07°卷绕角为例，分别对比了近似算法和精确算法所得纱长以及ZF/ZG理论值的区别，凸显了精确计算的优势。

5.2 基于精确计算，通过微分计算得出钢领板在上升状态时的瞬时速度vg和纱线卷绕转角θ的关系式，通过再次整理后，可用于计算伺服电机的对应瞬时转速。

[1] 中国纺织总会教育部.棉纺工艺学:下册[M].2版.北京:中国纺织出版社,1998:102-166.

[2] 陈人哲.纺织机械设计原理:上册[M].2版.北京:中国纺织出版社,1996:229-293.

[3] 同济大学数学系.高等数学:上册[M].6版.北京:高等教育出版社,2007:366.

[4] 刘全新.环锭细纱机的卷绕分析和参数调整[J].现代纺织技术,1999(Z1):18-22.

[5] 经纬纺织机械股份有限公司榆次分公司.FA506型环锭细纱机产品说明书[Z].

Comparison and Application of the Varieties of Yarn Length Counters on Winding Forming of the Ring Spinning Frame

WEI Jinping

(Jingwei Textile Machinery Co.,Ltd.Yuci Branch,Jinzhong 030601,China)

In order to get accurate length of the winding yarn length at each lift of the ring plate of the ring spinning frame,based on the transmission structure of the ring spinning frame FA506,comparison analysis is done to the counting difference of the winding yarn length between the approximate algorithm and accurate algorithm both in forms of the mechanical lifting and the electronic lifting.Discussion is made to the relationship between the rising speed of the ring plate and the yarn throughput speed of the front roller and the winding angle.It is pointed out that the approximate yarn length is greater than the accurate yarn length,and the approximate value of the winding gear pairZF/ZGis smaller than that of the accurate calculation,which is not conducive to forming and high-speed winding.Therefore,the electronic lifting should use accurate algorithm.Through analyzing the relationship between the instantaneous velocity and the winding angle at rising ring plate,the instantaneous speed of the servo motor can be worked out.

ring spinning;winding forming;mechanical lifting;electronic lifting；yarn length;approximate calculating;accurate calculating

2016-11-13

韦金平(1983—)，男，河南南阳人，主要从事环锭纺细纱机的设计工作。

TS104.1+5

A

1001-9634(2017)04-0005-04