对常微分方程数学建模案例的研究

郑玉敏

(黑龙江生态工程职业学院，哈尔滨 150000)

对常微分方程数学建模案例的研究

郑玉敏

(黑龙江生态工程职业学院，哈尔滨 150000)

案例教学法贴近学生们的实际情况，引出数学问题，进而转换为数学知识，加强了学生们对常微分方程在实际应用过程中的了解及对数学建模思想的理解，从而有效地提高了学生们的数学建模能力和学生们对应用数学的学习兴趣。所以，强化对常微分方程数学建模案例的研究，在高等数学教学与研究中具有十分重要的现实意义。

常微分方程；数学建模；案例分析

如今，越来越多的院校在高等数学课程的教学过程中应用案例教学法，因为案例教学法本身就是由贴近学生们的生活实际情境而引发数学问题，并转化为相应的数学知识，在运用学生们所学会的数学知识解决实际生活中所遇到的问题的一个过程。应用案例教学法不仅进一步缩短了实际生活情境与数学教学情境之间的差异，还对进一步提高学生们的数学学习兴趣，培养学生们的实践创新能力有着至关重要的作用。所以，做好案例教学法的应用也是各个院校开展数学教学工作所采用的重要手段。常微分方程作为高等教育的重要组成内容，绝大多数学生在常微分方程的学习过程中往往只了解如何去解方程，而不知道这些方案的真实背景，造成学生们在常微分方程的学习过程中缺乏学习动力、产生了消极的学习态度。案例教学法在数学授课过程中恰恰是由实际案例出发，使学生们更加清楚的掌握对常微分方程的应用，加深了学生们对数学建模思想的进一步理解，有效提高了学生们的数学建模能力和对问题的实际分析能力、解决能力。所以，在常微分方程的学习过程中将数学建模思想融入其中，能使学生们更好的掌握常微分方程的学习方法、学习背景、学习意义，从而最大限度的提高学生们对应用数学知识的学习兴趣。

以常微分方程中的若干习题为例，运用数学语言进行阐述，按照数学建模解决问题的思想对其进行科学合理的假设，构建微分方程模型，并让学生们运用所学的数学知识进行模型求解，使学生们在数学课堂上将所学到的数学内容与数学建模内容有机的融合，最终利用数学建模方法把数学建模思想表达出来，使学生们在学习数学课堂知识的同时，正确掌握数学建模思想，更好的掌握常微分的方程理论。

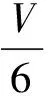
模型假设：第一，假设湖水的唯一水源就是河水，且湖水的实际容量不会发生变化；第二，假设湖水中污染物A的浓度始终都是均匀的；第三，假设当河水流入到湖泊以后能与湖水进行充分的融合，并且能在湖水中将全部的有毒污染物溶解。

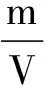
历经6ln3年以后，该湖泊中所包含的污染物A可以降到m0之内。

问题2：乘坐公共汽车的时候，对交通信号灯的等待是十分烦恼的问题，尤其是由红、黄、绿三种颜色组成的交通路口指挥信号灯，想要从绿灯转换为红灯必须要经过黄灯的过渡，黄灯需要亮起一段时间以后方可从绿灯转换为红灯。虽然这种设计十分科学、合理，能够最大限度的避免某个方向车流等待时间过长的问题，最大限度的减轻司机与乘客的烦恼，但是，如若交通指挥信号灯在闪烁时间设计上存在不合理性，人们不仅面临更加漫长的等待，也会进一步增加司机与乘客的烦恼，所以，应该科学、合理的设计交通路口指挥信号灯闪烁的时间，使其闪烁时间长短更加合理。

分析模型：黄灯信号具有两个作用：其一，提醒驾驶员注意红、绿信号灯，当红灯信号亮起的时候应立刻停车，让横向车流、人流通过，对于已经超过了停止线的车辆允许继续通过；其二，当黄灯信号亮起的时候，为确保机动车与行人都能在安全的原则下通行，车辆仍然会向前行驶一段距离L以后方能停车，假设道路宽度为D，此时的问题就是如何对L的大小进行确定。

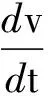
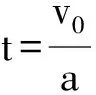
此时黄灯信号要亮起多久才最为科学合理呢？

通过上述公式的推导可以得知，从黄灯信号开始闪烁的时间算起，包括驾驶员看到黄灯信号时，准备开始停止机动车时所用的时间，以及让已经超过了停止线的机动车顺利通过路口所用的时间，黄灯信号最为科学、合理的闪烁时间应该为：

通过常微分方程解的各种属性研究对一些现象进行解释，从而对未来的发展趋势做出有效的预测，为人们设计新的装置提供重要的参考依据。所以常微分方程也是研究自然科学、工程技术乃至社会生活现象的重要工具。笔者对常微分方程中的部分内容进行了分析，在常微分方程中融入数学建模思想，使数学知识与实际生活内容紧密的联系在一起，并在教学过程中应用案例教学法，对案例进行分析，采取提出问题、分析问题、建立模型、求解模型的一系列教学手段，让学生们更加清楚的了解到常微分方程的实际背景，对所列出的常微分方程进行求解，更好地解决生活中所遇到的实际问题。这样不仅大大提高学生们对数学知识的学习兴趣和学习积极性，也大大的增强了学生们的数学学习能力。这种数学建模思想有着极为深远的意义，值得我们在数学教学中深入的研究与探讨。

[1] 廉海荣，赵俊芳，褚宝增.在“常微分方程”教学中融入数学建模思想的探讨[C]//城市空间结构理论与资源型城市转型研究——中国科协第224次青年科学家论坛，2010.

[2] 刘洪霞，周绍伟.常微分方程数学建模案例分析[J].河南教育学院学报(自然科学版)，2015，(12)：22-23.

[3] 方芳.常微分方程理论在数学建模中的简单应用[D].合肥：安徽大学，2010.

[4] 王莉.关于常微分方程课程教学模式的探索与研究[J].山东农业工程学院学报，2016，(08)：13-15.

Research on mathematical modeling of ordinary differential equations

ZHENG Yu-min

(Heilongjiang Ecological Engineering Vocational College, Harbin 150000, China)

Case teaching method is close to the actual situation of students, which strengthens the understanding of the practical application of ODE and mathematical modeling ideas, so as to effectively improve students’ mathematical modeling ability and their interest in applying mathematics. Therefore, it is of great practical significance to study the case of mathematical modeling of ordinary differential equations in higher mathematics teaching and research.

Ordinary differential equation; Mathematical modeling; Case analysis

2017-05-20

郑玉敏(1978-)，女，硕士，副教授。

O175.1

A

1674-8646(2017)13-0066-02