以特征值关联项改进贝叶斯分类器正确率

蔡永泉 王玉栋

(北京工业大学计算机学院 北京 100124)



以特征值关联项改进贝叶斯分类器正确率

蔡永泉 王玉栋

(北京工业大学计算机学院 北京 100124)

朴素贝叶斯分类器建立在其数据“特征值之间相互条件独立”的基础上，而在实际应用中该假设难以完全成立。针对这种现象提出一种算法，即通过寻找对产生错误分类影响最大的特征值，并依此特征值的关联项对数据项扩充，在此基础上对扩充项添加权重，以达到提升分类器精度的效果。最后对权重的大小加以论证，实验分析了不同大小的权重对分类器正确率的影响。实验结果表明，添加关联项扩充训练集，可以有效提升贝叶斯分类器的正确率。

朴素贝叶斯分类器 贝叶斯算法 贝叶斯分类器

0 引 言

朴素贝叶斯算法是一种在已知先验概率与类条件概率的情况下的模式分类方法，待分类样本的分类结果取决于各类域中样本的全体[1]。朴素贝叶斯分类器(NBC)以贝叶斯公式为基础，从理论上讲精确度高，运算速度快[2]，但也存在以下问题：(1) 在样本的特征提取不够优秀时，或对于易出现干扰项的样本，容易导致分类正确率低。(2) 样本中有部分数据特征稀疏，会极大地降低NBC分类结果的正确率。因此NBC一般情况下的分类效果难以达到理论高度。

1993年Agrawal等率先提出关联规则挖掘[3]，它可以对特征值之间的关系进行分析[4]。目前对关联特征值的关联项的研究主要是挖掘频繁集，采集的方法有多种，如Apriori、FP-tree、LPMiner。张阳等[5]曾提出一种类似Apriori算法的冗余剔除算法和特征值筛选方法，使关联特征值具有更好的分类能力。

本文在NBC的基础上，在经过一次训练后，通过训练结果筛选容易致误的特征值，并对所有错误分类的所包含的特征值进行提取，从中发掘关联项，对原训练过程中的样本集进行提扩充。以0-1分类(两类分类)为例，根据0和1两类的先验条件概率，考虑从样本集中提取最有可能产生错误结果的特征值，并依该特征值寻找关联点扩充原数据集，从而提高NBC的分类效果。

1 朴素贝叶斯算法

朴素贝叶斯分类方法(NB)是Maron等在1960年提出的一种基于贝叶斯定理的分类算法[6]。其“朴素”在于假设特征值之间条件独立且位置独立，即不同特征值之间不存在依赖关系且位置不存在依赖关系。

设T={t1,t2,…,tn}为一个未知分类的n维样本集合，C={C1,C2,…,Cm}为类别集合，贝叶斯分类算法的目标是将任意的样本ti分配到类别Ci则可以将贝叶斯分类算法阐述为：任取元组X，将在先验概率的基础上把X分类到后验概率最高的类[7-8]，即NB预测X属于类别Ci，当且仅当：

P(Ci|X)>P(Cj|X) 1≤j≤mi≠j

(1)

由贝叶斯定理知：

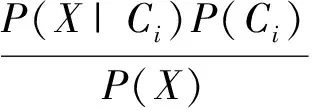
(2)

其中P(Ci|X)为事件Ci在X的情况下发生的概率，P(X|Ci)为先验条件概率，P(Ci)为先验类别概率。

对于事件Ci∈C和任意X则有：

(3)

其中sum(Ci)是类别Ci在总体样本中的数量，即无论哪个分类Ci下，X发生的概率P(X)都是相同的，因此贝叶斯公式在分类算法中可以近似地简化为：

P(Ci|X)=P(X|Ci)P(Ci)

(4)

而求解的过程便简化为求解P(X|Ci)和P(Ci)，其中的关键是计算先验条件概率P(X|Ci)。

虽然实际生活中鉴于特征值的复杂性，特别是在类别C非常复杂的情况下，计算条件概率P(X|Ci)非常困难，然而NB算法假设了元组X中的特征值相互独立，因此从该假设的基础上可以得出：

(5)

设函数c为一个函数，则贝叶斯分类器的目标为：

(6)

其中c(X)为满足argmax函数的条件，使得上式达到最大值。

2 问题分析

NB算法在实际中会遇到如下的问题，设想一个两类分类(以下简述为0-1分类)中，存在着0和1两类数据，当其中的一类中(假设为0类)频繁出现的某个特征值xi∈X，会有较高的条件概率P(xi|C=0)，而由此现象会有可能产生错误分类，但是这种错误分类产生有一定的特定条件，同样以0-1分类为例：

(1) 某个特征值在其中一类出现非常频繁，而在另一类中出现的几率较低。

(2) 误分类项本身较为稀疏。

根据式(6)可知最终分类结果取决于每P(xj|Ci)，因此当条件(1)发生时，会导致c(X)的选择出现一定的偏差。由于在NB算法中假设了相互独立，每个属性对总体概率的影响权重是相同的，即使发生条件(1)并不一定会导致误分类。

在数据预处理以及特征值提取较好的情况下，NB算法的分类效果较好。但是较好的特征值提取仅仅代表着特征值能较好地表征数据的分类归属，仍然不能避免上述两个条件的情况产生。在数据本身较为稀疏的情况下，甚至会因为个别特殊的特征值而直接产生错误分类。下面将从上述条件的角度出发试图分析并解决该问题。

3 寻找关联项

在机器学习的过程中常常采用交叉验证的方式，所谓交叉验证指的是在训练样本较大的情况下，随机地取训练样本的一部分作为测试集。本文在实验过程中采用了以下方式寻找会产生误分类的特征值。

3.1 通过结果反馈选择关联项

在交叉验证的过程中，对误分类项做标记。如果0分类项产生错误分类，被标记为1，则标记为错误项，反之同理。问题的关键是如何判断在错误项中哪些特征值是致误的。根据第2节中的两个条件，错误分类的关键特征值可以从如下步骤进行提取，以0-1分类为例：

(1) 找出错误的项，若0类误分为1，则可以判断在该项中的特征值中某些或某个在类别为1的条件下的概率过高。

(2) 找出所有P(xi|C=1)>P(xi|C=0)的特征值，作为keys。

(3) 选取一个key与在这些错误分类中包含的特征值联合，并扩充到全体训练集。

(4) 以扩充后的训练集重新训练。

(5) 寻找P(xi=key&xj|C=0)>P(xi=key&xj|C=1)中最大的关联特征值。

(6) 重复步骤(3)-步骤(5)选出最优的关联特征值。

(7) 按照以上步骤对把1类误分为0类的项执行操作，重新训练并验证。

给出算法伪代码(python风格)，该算法用于处理把0类误分为1类的项。

#val特征值列表，data2train训练集，data2test测试集，class为分类

def naiveBayes_com(data2train, data2test, class, val):

#p0V为P(xi|C=0) ,p1V为P(xi|C=1),P(C=0)

p0V, p1V, pA = train(data2train, class) # 注释1

#朴素贝叶斯分类结果dataSet，标记分类正误

dataSet = naiveBayes(p0V, p1V, pA, data2test)

# 步骤1，dataSet0_1：0类误分为1类的集合；val0_1：其中包含的特征值

# errorVals为val0_1和val1_0的并集

dataSet0_1, dataSet1_0,val0_1,val1_0, errorVals = sign(dataSet, class)

#p0V0_1是把0类误分为1的项的P(xi|C=0), p1V0_1同理

p0V0_1, p1V0_1 = getErrorP(p0V, p1V, dataSet)

#步骤2，计算差，提取符合条件的特征值作为备选keys

differP0_1 = p1V0_1 - p0V1_0

index = 0, pIndex = [], pList = []

for(p in differP0_1): #遍历一条中的每一项

if p>0: #P(xi|C=1)>P(xi|C=0)

pIndex.append(index)

pList.append(p)

index += 1

keysIndex= sorted(pIndex, pList) #注释3

conL = len(data2train[0]) - 1#data2train的维度

con = -1

conList = []#最终选定的关联项

for (errorVal in errorVals):#遍历errorVals

for (key in keysIndex):#遍历所有的keys

for (data in data2train):#扩充训练集

if data[errorval] >0 && data[key]>0:

data.append( 1 ) #用关联项进行扩充

else:

data.append(0)

conR = len(data2train[0]) - 1 #扩充后的维度

#扩充后的训练结果

p0V_new, p1V_new, pA_new = train(data2train, class)

conIndex = 0 #记录有效的关联项

for (con in range(conL, conR)):

if p0V_new[con]>p1V_new:

conIndex = con # 最大的关联项

conList.append(conIndex)

#命名新的关联项，并加入到val

return conList, val val.append(newItem(errorval, key))

在样本维度较大的情况下，上述算法基本不会破坏整体的“相互独立性”，但是同样因为其独立性，按照以上步骤寻找关联项必然存在着问题，具体实验结果如表1所示。

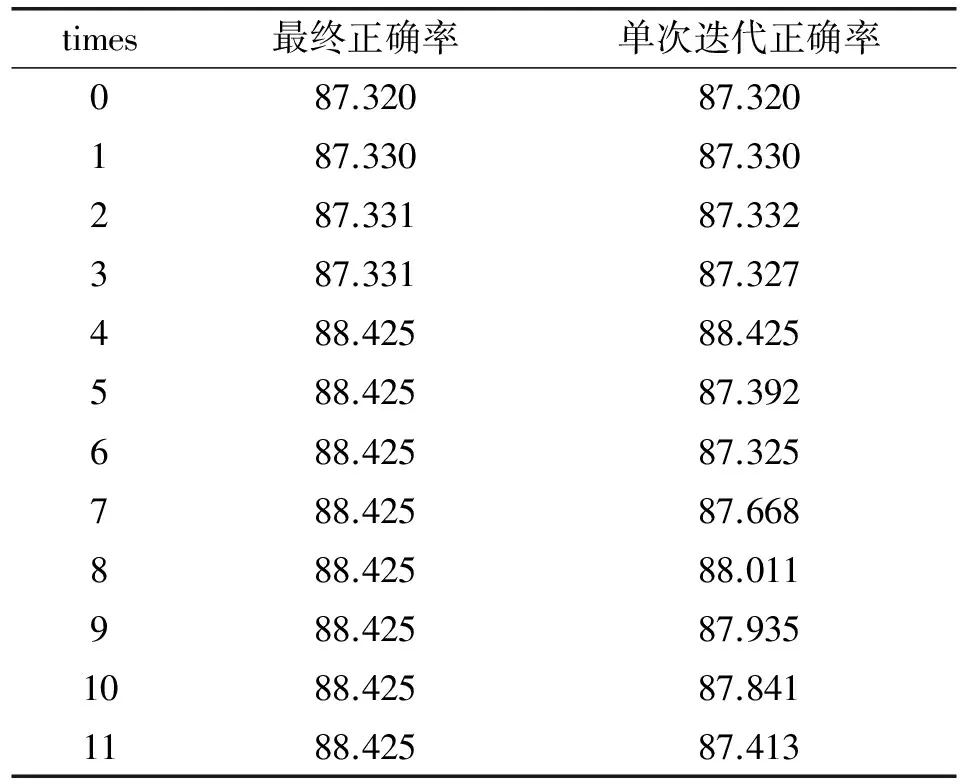
表1 naiveBayes_com算法正确率 %

该实验只寻找把0类误分为1类的一组最优的关联项，单次迭代正确率是实验过程中为了观测每次执行步骤(5)的执行效果而加入的观测量，第0次迭代代表着未进行关联项选取的正确率。实验共有11次迭代，每次迭代代表着选取了1组关联特征值，但不一定是最优的，第11次的迭代结果代表了最终的选择，可以看到从第4次开始已经找到了最佳的关联项。但就实验结果来看，无论是否寻找关联项，实验的效果都不好。

3.2 为关联项设置权重

由式(5)可知P(X|Ci)的值是极小的，若对特征值的提取稍有不恰当会使得出的概率值极低。这在设置权重的时候增加了难度，如果直接使用不仅会造成数据的下溢出，所设置的权重系数可能会极大或者极小。已知f(x)=ln(x)在(0, +∞)的空间上都是单调递增的，因此在实际操作时对P(X|Ci)取对数是可取的，即：

(7)

(8)

必须强调的是对极小的数据作处理有多种，这里选择ln函数的目的是因为即便概率低至百万分之一数量级也可以将权重控制在一个良好的范围内。再采用了上述算法选取最佳关联特征值后，将对该关联特征值训练后的条件概率添加权重。在设置权重的过程中将权重的范围设定在一个以0为起点且很大的取值域，逐步缩小两端点的范围并计算正确率。采用两端点的好处是可以观测权重在一定取值范围内的效果，避免陷入局部最优点。对权重取两端进行多次替换和迭代，逐渐缩小范围计算权重取两端点时的正确率，并选取正确率最大的点，使得左右端点逼近一个点，如图1所示。

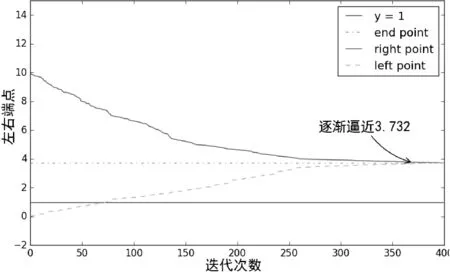
图1 左右端点(权重)随迭代次数的移动

随着迭代次数的增加，左右端点会逐渐逼近3.732，这是端点在本次实验的最优解。实际上这是一个求解最优解的过程，存在一个权重w，使得以下两式同时满足。

P(C=1|X)>P(C=0|X)C=1

(9)

P(C=0|X)>P(C=1|X)C=0

(10)

在这个过程中参数的选取原则是使得正确率最大，这要求权重的选取尽可能地照顾到0-1两类分类，即权重为0表示该关联项不存在，权重过小时关联项对整体的影响不明显，反之会将本来正确的一项变成错误的。

4 权重选取标准的探讨

权重的选择并不能仅仅把迭代的结果就按照最后的结果，由式(9)和式(10)推测权重w的取值很有可能是一个范围而不是一个常数，图2对该推测给出了实验结果。

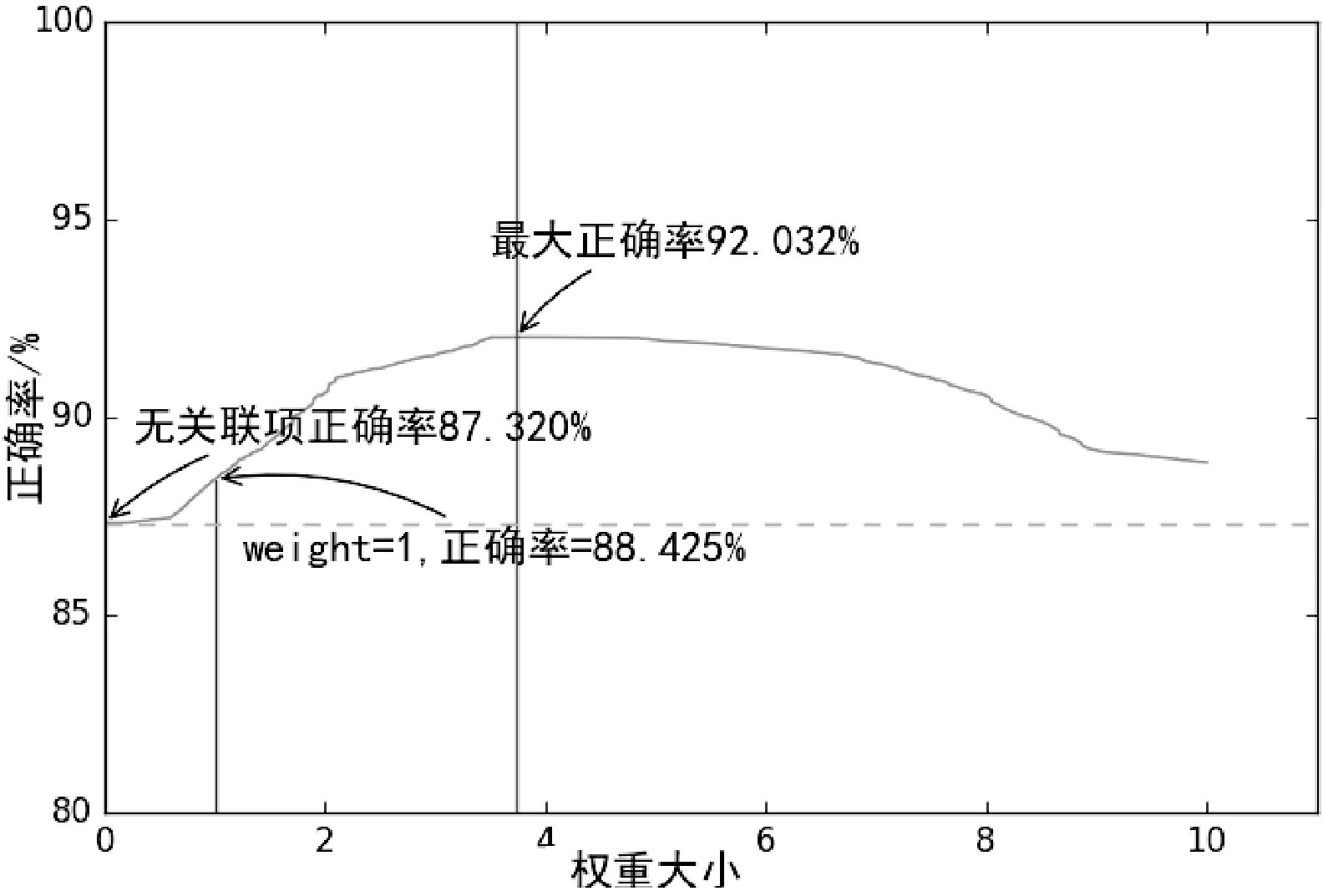
图2 正确率随权重改变

在权重接近于0时，关联项的影响很小，正确率基本没有变化，随着权重的增大，在3.732处为92.03%。可以直观地看到，在顶点处的一片区域内权重的变化对正确率基本没有影响，由实验数据得出在(3.506，3.848)之间的正确率都是92.032%，那么上述推测是可以成立的。

4.1 权重的选择标准

对任何一条数据X其分类标准是求解式(4)，并比较其后验条件概率P(C=0|X)和P(C=1|X)。在训练样本时，上述实验中所拟合的权重3.732仅从数据上讲是最佳的，但是在实际应用中应考虑到尽可能将训练器拟合到更复杂的情况中来，因此3.732仅仅是一个理想化的取值。为了使得训练器能适用于更多的样本，本文将给出评价训练的一个标准。

对于一条任意的样本数据X=[x1,x2,…,xn]，定义其概率方差D为：

[(a1+wb1)-(a0+wb0)]2=

(a+bw)2

其中P(C=1|xi)为一条样本中的一个特征值的概率，a1和a0为对样本概率取对数后的不设置权重的部分(该部分的权重是1)，可以近似地归为常数部分，b0和b1为关联项的概率，这样便将D近似地转化为一个关于w的二次函数。

4.2 概率方差的意义

在方差D的式子中，对w求导数，在拐点处D得到一个极小值，反之在一定的取值范围内，显然越靠近该取值域的边缘D的值越大，此时总体上P(C=1|xi)-P(C=0|xi)的绝对值是最大的，使得一条样本在不同的分类之间的差距最大，那么权重才能更好地拟合复杂样本。就上述实验而言，在取值域(3.506，3.848)之间，总是靠近区间两段的点使得方差D最大，这是权重w的最优的取值。

5 多个关联项的选取

上述的所有实验中，只选取了一个关联项，即是从将0类误分为1类的样本中通过改进的NB_C算法中选取了一个关联项。在多关联项的选取中，根据NB算法的相互条件独立的假设，本文总是每次选择一个关联项，并对每个关联项设置最优的权重。这种方法在只用一个关联项扩充训练样本的情况下是最优的，而多关联项的情况下，由于每个关联项都设置了权重，在一定程度上拉动了整体的概率，所以正确率并不是最好的。因此本文采用对所有的权重采取批量百分比下降和上升的方法，对每一次下降和上升的步长设定在一定得范围内，通过比较两次批量下降和上升后正确率上升的斜率来控制下一次的步幅，其中每次的斜率定义为：

k=(本次的正确率-上次的正确率)/下降步幅

通过这种方法，可以在两端同时逼近整体最优点时逐渐缩小步伐。

在对权重作批量更新时，应该考虑到保存每一次的最优情况，当遇到最优情况时，应越过最优点，继续下降或上升，因为整体权重的调整范围是0至100%之间，因此总能找到一个最优点而不会进入局部最优点。

表2描述了多个selectedCom0_1(从把0类误分为1类中提取)和selectedCom1_0下使用测试集测试的算法正确率，共选择合格的selectedCom0_1项11个和selectedCom1_0项6个。在训练过程中，假设关联项之间是相互独立的，然后分别训练每个关联项，并赋予权重。最后对所有的权重采取批量百分比下降和上升的方法选择最优权重。可以明显看出，随着关联项的增多，正确率是单调增加的。这是因为每个关联项都无法覆盖所有的样本，更多的关联项意味着能更好地覆盖样本。

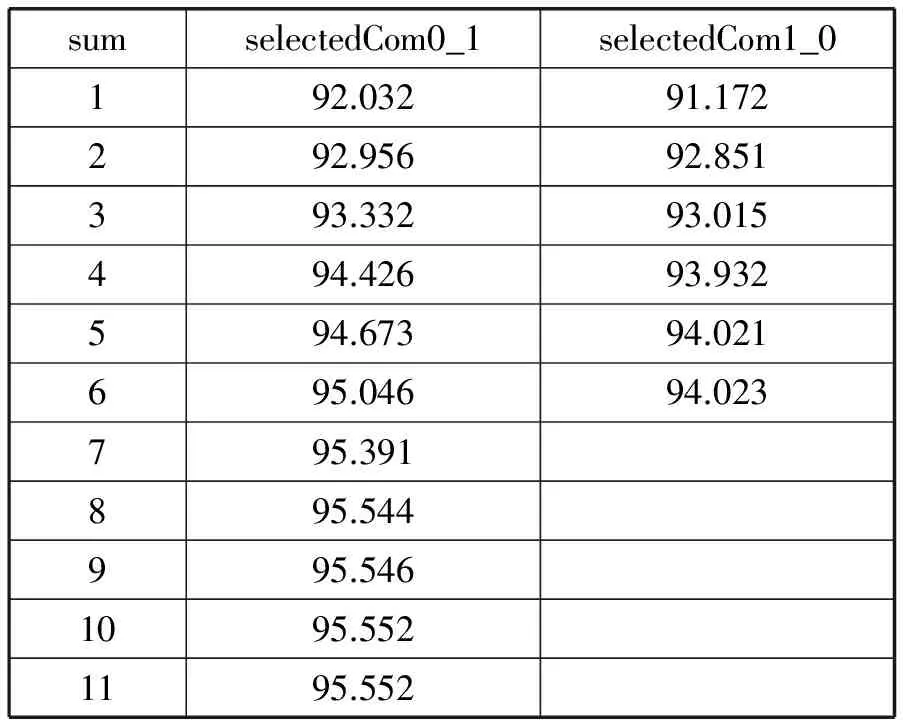
表2 多关联项下的准确率 %

表3给出了多个关联项下的正确率。因为本文所用的数据集的维度远超关联项的个数，且关联项大多数覆盖的是误差项，所以统计了所能罗列的所有关联项。可以明确地看出当关联项增多的时候整体正确率并不是简单的累加，并在数目达到最大的时候，算法的正确率已经收敛，这说明关联项之间已经产生了一定的相关性，设置关联项的数量应该控制在一定的范围内。

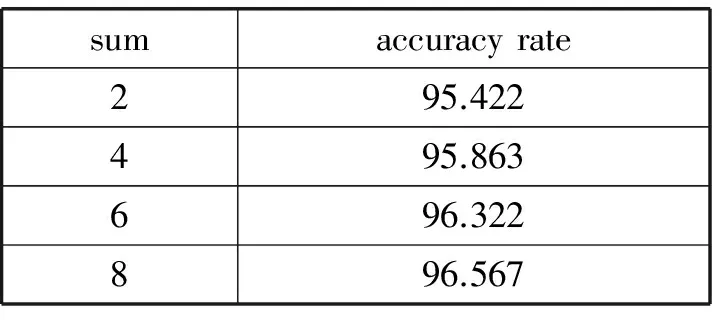
表3 多关联项下的准确率 %

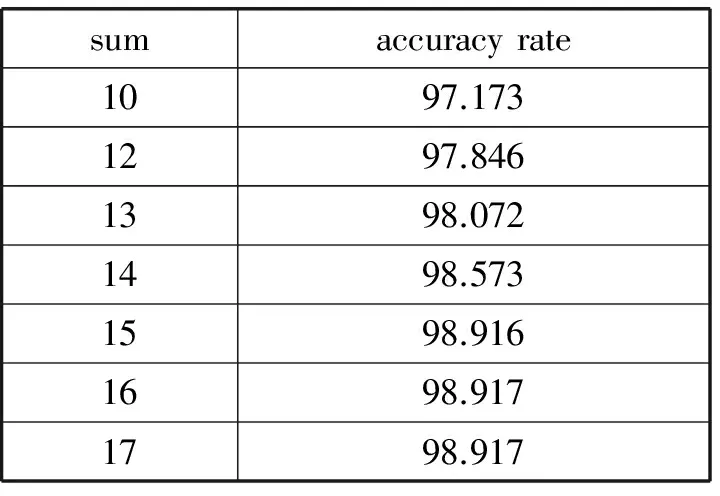
续表3 %

6 结 语

通过一次分类结果从误分类样本出发，寻找会产生错误的关键特征值。根据关键特征值选择关联项，为关联项添加权重改善对整体概率的调整能力，并利用方差最大化，使得训练更加拟合复杂样本。通过训练多个关联项使其更好地覆盖整体样本，并且单独为每个关联项设置权重，最后批量调整权重。

本文在朴素贝叶斯分类器的基础上进行研究，对分类器的问题作了分析，以误分类样本作为起点，对朴素贝叶斯算法进行改进。加入了一种简单的寻找关联项的方法，并对关联项的权重作了深入探讨，提高了朴素贝叶斯算法的分类效果。

[1] 陈凯,朱钰.机器学习及其相关算法综述[J].统计与信息论坛,2007,22(5):105-112.

[2] Efron B.Bayes’ theorem in the 21th century[J].Science,2013,340(6137):1177-1178.

[3] Agrawal R,Imieliński T,Swami A.Mining association rules between sets of items in large databases[C]//ACM SIGMOD International Conference on Management of Data.ACM,1999:207-216.

[4] Zhang H,Sheng S.Learning weighted naive Bayes with accurate ranking[C]//IEEE International Conference on Data Mining.IEEE Xplore,2004:567-570.

[5] 张阳,张利军,闫剑锋,等.基于关联特征的朴素贝叶斯文本分类器[J].西北工业大学学报,2004,22(4):413-416.

[6] Maron M E,Kuhns J L.On relevance,probabilistic indexing and information retrieval[J].Journal of the ACM(JACM),1960,7(3):216-244.

[7] 陈新美,潘笑颜,路光辉,等.基于朴素贝叶斯的局部放电诊断模型[J].计算机应用与软件,2016,33(9):51-55.

[8] 蒋礼青,张明新,郑金龙,等.基于蝙蝠算法的贝叶斯分类器优化研究[J].计算机应用与软件,2016,33(9):259-263.

[9] Zhu J,Chen N,Xing E P.Bayesian inference with posterior regularization and applications to infinite latent SVMs[J].Journal of Machine Learning Research,2014,15:1799-1847.

IMPROVENAÏVEBAYESCLASSIFICATIONWITHRELATEDITEMS

Cai Yongquan Wang Yudong
(CollegeofComputerScience,BeijingUniversityofTechnology,Beijing100124,China)

Naive Bayes classifier is based on the hypothesis that parameters of the sample are mutually conditional independent. The practical application of this hypothesis is hard to established, so this paper proposes a new algorithm to improve Naive Bayes classifier through looking for properties that have the maximum influence on error classification with an effectively way, finding related items to extend the original data set, then adding weights to the related items. This paper shows the results by experiments, and related items make the classifier work better.

Naïve Bayes classification Bayes algorithm Bayes classifier

2016-10-15。蔡永泉，教授，主研领域：信息安全。王玉栋，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2017.08.051