基于博弈论的航空运输增值服务动态定价模型研究
李常亮
(中国民航大学 天津 300000)
基于博弈论的航空运输增值服务动态定价模型研究
李常亮
(中国民航大学 天津 300000)
收益管理一直是航空运输业最重要的问题之一,而其中票价的研究是重点。航空运输业发展到现代,其收益越来越趋向于多元化,除了机票本身的价格外,航空公司也开始重视发展增值服务,将其作为提高行业竞争力的筹码之一,但目前形成动态的定价模型还很少。基于此种状况,本文利用博弈论建立起航空公司和旅客之间的Nash均衡,形成优化函数,构建了了相关模型。
航空运输;博弈论;增值服务;动态;定价
一、序言
航空业作为服务行业自产生以来就不断在优化自身的服务能力,尤其伴随着航空业在各国逐渐走向市场化,竞争日趋激烈,各航空公司更加重视增值服务带来的效应,但目前增值服务的定价没有合适的定价模型可用,基本上是靠航空公司根据简单的收入成本分析进行定价,且考虑因素简单,可以预见的是随着增值服务收费研究的细化和深入,现有的这种定价方式难以满足市场需要。
针对以上问题笔者给定假设,认为未来航空票价基本市场化,裸机票价很低,航空公司可以对每一个可利用的有效座位实行个性化的增值服务收费,利用博弈论来对航空公司和旅客之间分析,建立动态的增值服务定价模型使航空公司收益最大化。
二、航空公司与旅客关于增值服务票价博弈分析
对于航空公司,可行的方案集为航企可接受的裸机价格到加上享受相应的增值服务的价格之间的全部价格集合。而对于旅客,可行的方案集为购买增值服务和拒绝任何增值服务。在销售增值服务销售过程中,航空公司首先进行制定增值服务价格的决策,然后旅客在获知航空公司决策之后根据增值价格来选择是否购买。
局中人1为航空公司,局中人2为旅客,假设fi(i=1,2,…)为航空公司可行的增值服务票价方案,U,V是增值服务fi的函数,分别为航空公司和旅客相应的收益,Y为“接受”,N为“拒绝”,形成动态博弈。
局中人1的航空公司能否得到收益。取决于局中人2的决策。设局中人1做出的最优决策为f*,它应该满足以下条件:U(f*)=max(U(f)),V(f*)>0.
动态的博弈中,首先是局中人1先行动,局中人2在获得局中人行动的信息后才去相应的行动。在这种情况下符合两种最大利益的纯策略局势为(f*,Y),除此之外的任何局势都会使得局中人1或2的利益得不到保障。所以该动态的纳什均衡为(f*,Y)。
三、旅客选择成本分析
在求解该动态的纳什均衡局势中需要用到旅客的收益计算,设旅客的收益函数为V,总的选择成本为C,则:V=C-f*;C=CP+CV
式中:CP为公务舱或头等舱与经济舱的价格差。CV空中旅行成本,这里指这样一部分经济舱旅客:而愿意付费到合适的位置。
CP对于所有在经济舱有增值服务需求的旅客来说是一个确定的常数,而CV是一个定性的指标,由于本文的重点不在这里且量化过程复杂繁琐,并且在航空公司进行处理时的意义不大,所以这里不再进行量化处理。
所以在航空公司的增值服务定价过程中,应该以CP为考虑重点。根据模型,在局中人1航空公司做出决策f*后,收益V>0的旅客将会选择接受增值服务的定价。因此,接受定价的旅客人数可以通过C>f*的概率来求解,其表达公式为:P(C>f*)=F(f*)
这里:F为C的补分布函数
假设F为线性函数,根据已有的统计数据可以得到:F(x)=ax+b。设当飞行时间大于2小时以上时在经济舱内有增值服务需求fmin的旅客比例为θ(θ随着飞机时间的长短变化而变化)。同时认为当飞行距离越来越长时,在经济舱有不同程度增值服务需求fmax的旅客将达到100%,即
求解方程组得
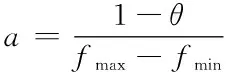
四、增值服务定价动态模型
通过以上博弈分析后可知,在足够长的飞行时间内的最优的增值服务定价组合就是局中人1航空公司的Nash均衡策略:
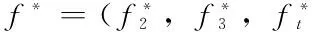
式中t为飞行时间,这里限制t不小于2.
当每个飞行时间点上有增值服务需求的旅客数量大于1时,航空公司对结局的决策影响就转化为了对有增值服务需求旅客人数的影响,此时,原来的双人博弈就退化为航空公司的单人博弈。
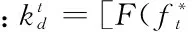

为了有效的计算收益期望。这里把总收益视为有销售(U+)损失(U-)两部分收益组成,得出总得收益期望为:E(U)=E(U+)-E(U-)
将在飞行时间为t的选择增值服务的旅客数量看着强度为λt的Poisson过程(时间连续状态下的离散马尔可夫过程),则有销售收益的数学期望:
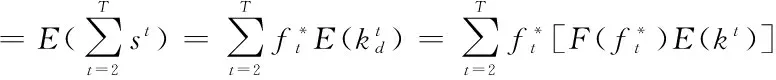
购买机票的旅客登机或no show可以看成是二项式分布,在实际的随机过程中认为noshow旅客之间是相互独立的,所以以概率pn来表示每一个发生在购票成功旅客身上的noshow。同样可以得出发生noshow和DB后给航空公司带来损失的的期望:
综上可得,增值服务动态定价问题的纳什均衡可由以下问题进行求解:
在增值服务实际的预定过程中,由于航空公司的航线长短以及飞行速度不具有连续性,所以上式中的可行域为非连续性,属于离散性质的可行域求解问题。为方便对该方法进行特性研究,实际运行中可以把可行域当作连续的可行域来对待,采用优化函数对模型进行实际运作。
五、结论
随着现在我国民航业市场化改革的深入,在价格上的管制也将达到前所未有的放松,如何有效的调节定价就成为一家航空公司的核心竞争因素之一,本文构建的模型具有可行性和一定的实用性,相关航空公司可以以此为模型进行收益管理。
[1]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2006
[2]梅虎,朱金福,汪侠 基于博弈分析的航空收益管理定价研究[J].预测,2006(6):45-49.
李常亮,男,汉族,中国民航大学经济与管理学院,管理科学与工程硕士,研究方向:航空运输经济。

