荷叶自清洁效应理论建模与分析
徐兆恒
摘 要:自古以来人们一直赞美荷叶的“出淤泥而不染”的高贵品质,该现象是由于荷叶表面具有超疏水自清洁的功能。随着科技的发展,这种由荷叶启发的自清洁功能已在建筑、纺织等行业有了广泛的应用。本文通过力学分析,揭示了超疏水自清洁效应产生的机理,并建立了相应的理论模型。通过实例分析,我们发现水滴的体积大小与超疏水材料的自清洁能力关系密切。最后,本文还给出了提高材料自清洁性能的设计方法,比如降低固体比例分数以及提高本征接触角大小等。
关键词:荷叶;自清洁效应;超疏水结构;液滴;粘附功
中图分类号:O414.1 文献标识码:A 文章编号:1671-2064(2017)13-0196-02
1 概述
虽然荷叶从污秽的泥水中长出,但是它却能持久地保持表面干净。这种“出淤泥而不染”的高贵品质实际上是由其表面的自清洁功能保证的:荷叶表面上的水滴可以在轻微的扰动下滚动离开原位置,并在滚动的过程中带走表面的灰尘和泥土,从而保持荷叶的清洁。出现自清洁效应的根本原因在于水滴与荷叶表面的粘附力非常低。这种水与固体之间粘附力极低的现象被称为超疏水现象。由于具有超疏水自清洁功能的材料无需人工维护就可保证表面的干燥清洁,极大的降低了人力成本,人们大量地将此类材料应用于如涂料、纺织品、玻璃、建筑等领域[1]。此外,一些特殊的超疏水自清洁材料还兼具抗结雾、抗结冰的能力,而这些功能可以在眼镜、汽车挡风玻璃等应用中大放异彩[2]。
通过观察荷叶表面的生物学特征,本文探究了它具备超疏水自清洁效应的物理机制。基于理论模型,我们通过实例分析了水滴与荷叶仿生材料之间的粘附作用,并提出了提高材料自清洁功能的方法。
2 超疏水现象力学建模
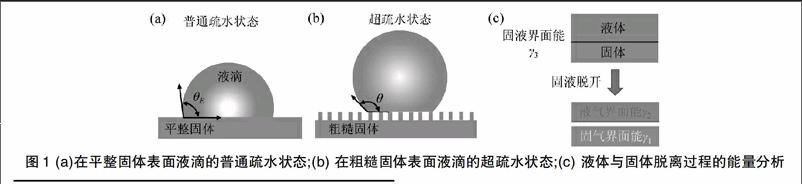
固体与水滴之间的粘附程度可以采用表观接触角这个几何量来表示。当小于90°时,固体亲水;当大于90°时,固体疏水;若大于150°,则为超疏水。当固体表面平整时,我们将相应的记为固体材料的本征接触角,如图1(a)所示。研究者已经证实,固体材料的本征接触角不可能大于120°,所以为了实现超疏水的接触状态,固体表面必须是粗糙的。采用电子显微镜观察荷叶的表面后,人们发现肉眼看上去似乎光滑的荷叶表面在微米尺度是非常粗糙的:正是由于这些粗糙度的存在,荷叶才具有超强的疏水能力以及自清洁功能。
如图1(b)所示,当一滴水滴静止于粗糙固体的表面时,粗糙突起之间包裹的空气(白色)会阻止固体与水之间发生更多的接触。由于固液之间的接触程度降低了,所以水滴更不容易粘在固体表面上,即固体的疏水性也相应地提高了。设f为描述固体与液体之间接触程度的参数,称为固体比例分数。根据定义,f=1代表没有空气隔离固液接触的情况,f=0代表固体与液体完全被空气隔离的情况。那么,根据如上描述,粗糙表面的接触角和本征接触角之间有如下关系:
(1)
根据公式(1),可以得到,当f=1时,,代表水滴置于平整固体表面的情况。当固体表面粗糙化后,f趋于0,使得趋近于-1,表观接触角接近于180°,即在固体表面液滴的外形近似为球形。此时,材料就具有超疏水的性质:液滴很容易在固体表面滚动并滑落。如果液滴要从固体表面滚落,则必须提供一定的能量。如图1(c)所示,我们考虑固液接触以及固液脱开两种状态。在接触状态下,系统能量主要为固体-液体界面能γ3;在固液脱开后,系统能量存在于固体-气体界面和液体-气体界面,能量大小分别为γ1和γ2。我们定义:
(2)
基于定义,W代表脱开单位面积的固液界面所需要的能量,即粘附功。根据著名的Young方程,我们还有如下关系。将该公式带入公式(2)中,我们最终可得[3]:
(3)
公式(3)显示,当固体的表观接触角接近180°时,W趋于零,即液体非常容易与固体脱开。
3 自清洁材料的优化设计
我们通过以下实例来探讨如何优化超疏水材料的自清洁功能。假设仿生荷叶材料具有如图1(b)所示的表面结构:表面结构为具有正方形截面的柱状阵列,且方柱的宽度a为20μm,方柱中心之间的距离d为50μm,那么根据固体比例分数f的定义,有f=a2/d2=0.16。令方柱结构的本征接触角为120°,基于公式(1),该材料的表观接触角应为156.9°。
当水滴处于固体表面时,如果不考虑重力的作用,其形状为球冠形。如果设水滴形成的球冠半径为R,那么液滴的体积V可表达为
(4)
且水滴與超疏水材料接触部分的底面面积A为:
(5)
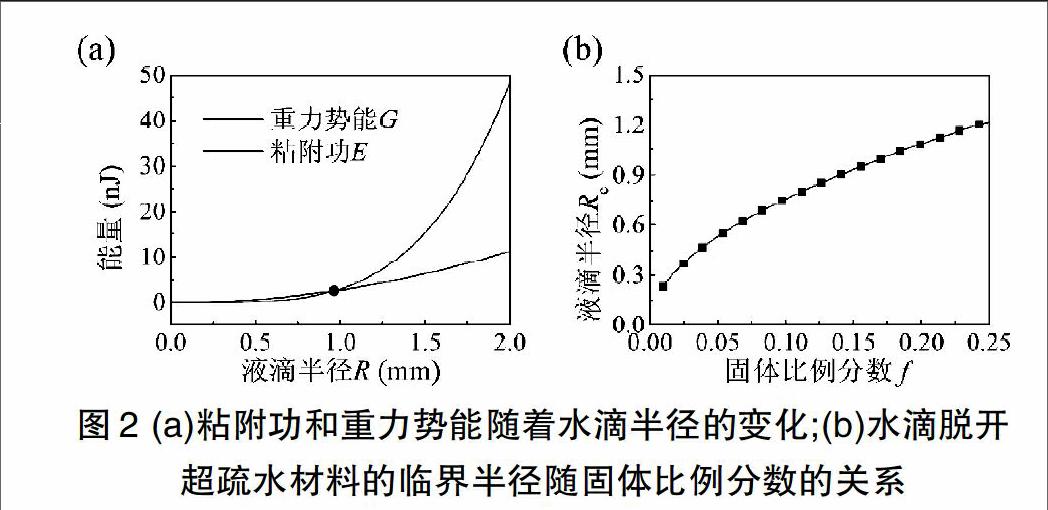
那么当水滴的半径R为2mm时,其体积V为33.4μL,底面面积A为1.93mm2,则水滴脱开固体所需要的能量,其中水的γ2为73mN/m。记水滴的重心高度为h,则h=1.85mm。由于水滴离开材料后重新形成半径为r的球形,则水滴在脱离材料后重心运动了mm。如果倒置超疏水材料,水滴的重力可以提供势能,其中为水的密度1000kg/m3。由于G大于E,说明该水滴可以克服材料表面的粘性,并离开材料表面。
当水滴的体积改变时,脱离超疏水材料所需要的粘附功以及水滴重力做功也会相应地改变。保持其他物理量不变,仅改变水滴的半径R,我们可得E和G的变化关系如图2(a)所示。根据计算结果我们可知,当液滴半径小于0.96mm时,粘附功E大于重力势能G,说明水滴的重力不足以克服粘附约束,即无法发生自由的滚动。这个现象意味着,体积越大的水滴越容易在超疏水材料表面发生滚动,即自清洁功能的实现需要依靠较大的水滴完成。
记水滴临界脱开超疏水材料表面时,其半径大小为Rc。例如对于图2(a)的情况,Rc=0.96mm,如图中圆点所示。为了提高仿生材料的超疏水自清洁功能,我们必须要使得水滴更容易在材料表面滚落,即降低Rc的大小。一种方法是,降低超疏水材料的固体比例分数f:如果采用该方法,表观接触角θ会增大,根据公式(5),水与材料之间的接触面积A以及粘附功E会随之降低。从而,降低f可以很好的降低Rc的大小,即提高自清洁能力。如图2(b)所示,当固体比例分数为0.01时,水滴的临界滚落半径下降到0.23mm。除了降低固体比例分数f之外,基于公式(1),我们可知,增大固体材料的本征接触角也可以实现相应的功效,并提高仿生荷叶材料的超疏水性能。
4 结语
通过对荷叶的观察,我们建立了描述超疏水现象的物理方程,并发现了固体表面粗糙度是实现自清洁功能的关键。利用接触角以及粘附功的概念,我们分析了水滴在仿生超疏水材料表面滚动的条件。结果表明,体积越大的水滴越容易在材料表面滚动,即自清洁功能主要是通过大水滴完成的。为了提高自清洁能力,设计者可以降低材料的固体比例分数或者提高本征接触角的大小。
参考文献
[1]瞿金东,彭家惠,陈明凤,等.自清洁外墙涂料的研究与应用[J].涂料工业,2006(1):43-47.
[2]彭娜.超疏水纳米氧化锌的制备及防覆冰抗结霜性能研究[D].南昌航空大学,2016.
[3]张泓筠.超疏水表面微结构对其疏水性能的影响及应用[D].湘潭大学,2013.

