基于Pareto优化理论的多目标超椭梯度线圈设计∗

潘辉王亮 王强龙 陈利民贾峰 刘震宇†

1)(中国科学院长春光学精密机械与物理研究所,长春 130033)2)(中国科学院大学,北京 100039)3)(德国弗莱堡大学医学院医学中心放射学系医学物理科,弗莱堡 79110)

基于Pareto优化理论的多目标超椭梯度线圈设计∗

潘辉1)2)王亮1)王强龙1)陈利民1)2)贾峰3)刘震宇1)†

1)(中国科学院长春光学精密机械与物理研究所,长春 130033)2)(中国科学院大学,北京 100039)3)(德国弗莱堡大学医学院医学中心放射学系医学物理科,弗莱堡 79110)

(2016年12月21日收到;2017年2月6日收到修改稿)

磁共振系统梯度线圈设计是一个多目标优化问题,在设计时需要综合考虑能耗、磁场能、线性度等设计要求.这些设计要求通常难以同时获得极小解,因此在设计梯度线圈时需要权衡线圈的各方面的设计需求.本文基于柱面可展性和流函数设计方法,结合Pareto优化方法实现了在超椭圆柱设计表面上梯度线圈的多目标设计.分别分析了磁场能、能耗目标对梯度线圈线性度、线圈构型的影响;并在Pareto解空间中分析各目标的相互变化关系,通过数值算例验证了该方法在超椭梯度线圈设计时的有效性与灵活性.优化结果显示,在满足线性度误差小于5%,能耗与磁场能分别小于用户设定值的设计约束下,梯度线圈的多目标设计存在多个局部优化解.该方法可以直观地比较相同目标函数值的情况下各单目标的具体表现,有利于实现不同的设计要求下梯度线圈的最终定型设计.

梯度线圈,流函数,超椭圆柱面,Pareto优化

1 引 言

磁共振成像作为一种非介入式影像技术,能够反映物体内部的层次结构.在过去的几十年,磁共振成像已经成为医疗诊断、生物研究、材料研究等领域的重要途径之一.磁共振成像是利用预先定义的可控磁场(如线性梯度磁场)来编码信号的空间位置信息［1].因此磁场的线性度、均匀度、强度将直接影响设备成像的效果.梯度磁场由线圈产生,通常布置在圆柱表面上,但为了更好地满足医疗需求,本文采用在超椭圆柱表面上设计梯度线圈的方法,以期减少被检测者的幽闭恐惧症［2].

现有梯度线圈的主要研究方法有目标场法和流函数法.目标场法在1986年由Tuner首先提出,结合Fourier变换求解电流密度［3,4].在此基础上,该方法被应用到双平面、圆柱面等设计表面;文献[5—9]进一步发展了圆柱面等简单规则设计曲面的目标场法.流函数法［10−13]是基于有限元离散求解的思想,更适应于复杂曲面的梯度线圈设计.现有的算法实现方式主要有直接法、镜像法和有限元法［14];王秋良课题组［15,16]在此基础上进一步实现了算法的改进与快速计算.近二十几年的发展中,梯度线圈的设计研究在磁场线性度、均匀性方面有了很大的进展［17,18],但成像响应时间、能耗、振动与噪音等性能指标仍需要进一步优化,从而提高仪器的效率.响应时间与电感直接相关,降低线圈总电感值不仅可以减少能耗,还可以减小磁场的涡流效应.本文利用流函数法以梯度线圈的电感值、能耗等为优化目标进行设计研究,从而减小线圈响应时间,降低能耗.

为了提供更好的性能和患者使用时的舒适度,理想的线圈同时具有最小的磁场能、最高的电磁转化率、最小的电阻、较好的磁场线性度、较短的响应时间以及较低的由洛伦兹力引起的噪音等性能.然而,该问题并不存在一个同时使所有目标性能最优的解,而是可能存在一系列权衡各性能的局部最优解.因此需要同时优化多个目标来获取更好的综合性能.另一方面,梯度线圈设计问题属于多目标问题［17−25],以单个磁场线性度为目标来求解具有不存在惟一解、线型振荡等问题.之前的研究中,为避免这类问题采用Tikhonov正则化方法构建目标函数［2],但该方法并无对应的实际物理意义.本文结合Pareto优化理论［23]对磁共振系统梯度线圈的线性度、能耗、磁场能等多目标进行优化分析.

2 理论方法

目前,磁共振梯度线圈的设计方法主要可分为目标场法和流函数法.相对于目标场法,流函数法具有更加灵活、适应复杂设计曲面的优势.本文采用流函数法进行分析计算.梯度线圈设计是一个多目标优化问题,需综合考虑磁场的线性度、磁场能、线圈的能耗等因素.

2.1流函数法

流函数法相对于目标场法将电流密度的矢量求解转化为流函数ψ的标量求解,简化了求解过程,更适应于超椭等复杂曲面的线圈设计.故本文采用流函数法在超椭圆柱设计表面(图1)上进行线圈的优化设计,电流密度J可表示为

其中,ne= (nex,ney,0)是超椭设计表面［2](x/a)2/m+(y/b)2/n=1的单位外法向量;nex,ney分别是单位外法向量ne的x,y方向分量;a,b分别是超椭圆的长短半轴的半轴长;m,n∈(0,1].

图1 超椭设计表面与ROI及设计表面的展开面Fig.1.Current-carrying surface Γcoil,ROI,and the developed design surface.

根据Biot-Savart定律,目标区域(region of interest,ROI)内第i点的磁场强度z方向分量可表示为

其中,

Zu,Zl分别是超椭圆柱面Z轴向的上下边界;(ri,θi,zi)是ROI的场点坐标,(θ,z)是超椭设计表面展开坐标.

利用有限单元法分片逼近的思想［2],超椭圆柱面展开平面上的流函数ψ可表示为

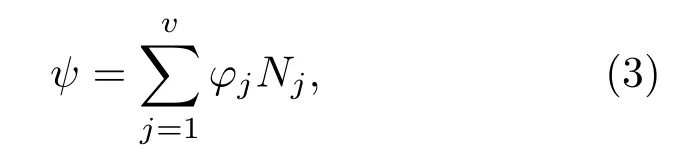
其中φj为各节点值,Nj为插值函数,v是设计表面Γcoil上各节点的自由度总和.

2.2梯度线圈设计目标和约束

本文中根据梯度线圈的性能的重要性以及病人的舒适度,在超椭圆柱设计表面上对梯度线圈的线性度、能耗和磁场能进行了多目标优化.

2.2.1 磁场强度与线性度

磁共振系统成像的原理在于利用线性的梯度磁场Gx,Gy,Gz来区分不同空间位置的磁共振信号,实现空间定位［1].梯度线圈产生的磁场分布逼近目标梯度磁场分布是实现其定位功能的基本要求.因此,在已有的梯度线圈优化模型中,都将ROI内真实磁场强度z分量的真实值Bz与理想值的偏离值和作为优化的主要设计目标,可表达为

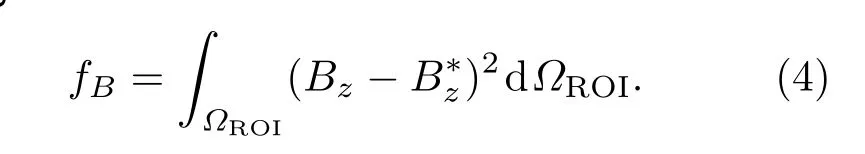
磁场线性度在工程中是衡量线圈成像质量的一个重要参数.梯度磁场的线性度将直接影响到成像的质量,线性度越高,空间定位越精确,获得的图像质量就越好.磁场线性度可用最大线性误差gΔBz来衡量:

2.2.2 梯度线圈能耗

梯度磁场需由梯度线圈通过电流驱动产生,在此过程中会由于线圈的电阻产生大量的热量,造成设备过热、能源消耗过多等.因此在设计优化中,将考虑由于线圈电阻产生的能耗,从而提高线圈的电磁转换率.在实际计算中,线圈的能耗可表示为

其中,σ为电导率,t是导电层厚度.

根据能耗fP与电阻R、电流I的关系,可以求出表征线圈性能的重要参数之一线圈的电阻R.

其中I线圈电流,计算中一般取I=(ψmax−ψmin)/N,ψmax和ψmin分别是流函数的最大值和最小值［11],N是线圈圈数.

2.2.3 梯度线圈磁场能

在磁共振设备工作时,需频繁切换线圈的电流来达到成像定位的作用.因此线圈的电感将直接影响到设备的响应速度与成像时间.而磁场能的大小反映了线圈的电感值,优化磁场能将等效于优化线圈电感［4,19].

磁场能与电感的关系表达式:

在该问题中磁场能可由(9)式求得

其中,A是磁位移矢量.由于在非设计区域J=0,所以磁场能可写成

2.3多目标优化

2.3.1 Pareto多目标优化

实际工程问题的优化大多基于多约束条件下的多目标优化问题.对于某些等式或不等式约束条件,可转化为辅助优化目标.要得到满足各要求的优化解,需对各个目标、约束进行权衡并建立适于求解的多目标函数形式［26−28].多目标的一般函数形式为

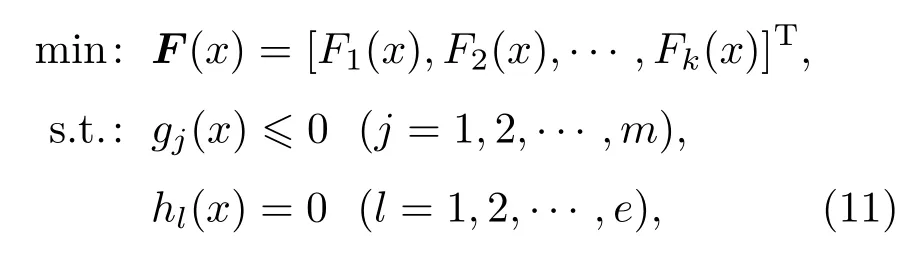
(11)式中Fk(x)为第k个子目标函数,gj(x)为第j个不等式约束,hl(x)为第l个等式约束.Pareto优化［23]是指有且仅有x∗∈X 使得对于x∈X有F(x)≤ F(x∗),并且至少存在一个目标函数有Fi(x)≤ Fi(x∗),则点x∗为Pareto优化. 当有且仅有x∗∈X对于x∈X不再存在x使得有F(x) ≤ F(x∗),则点x∗为弱Pareto优化. 若有Fo∈ Zk,如果对于每一个i=1,2,...,k,都存在则x为理想点.

多目标优化有一些用来判断评定优化方法最终效果的概念,最常用的两种概念是多目标优化必要条件和充分条件.如果一个多目标优化形式提供一个必要条件,对于一个Pareto优化点,则必为此多目标优化形式的解.对于提供必要条件的多目标优化形式,可通过调整参数来获得所有的Pareto优化点,如果一个多目标优化形式提供一个充分条件,则其解为Pareto优化,但是一个确定的Pareto优化点可能无法获取.

2.3.2 梯度线圈的多目标优化

梯度线圈的优化需要综合考虑上述线性度、能耗、磁场能等目标及约束［13],可表达为

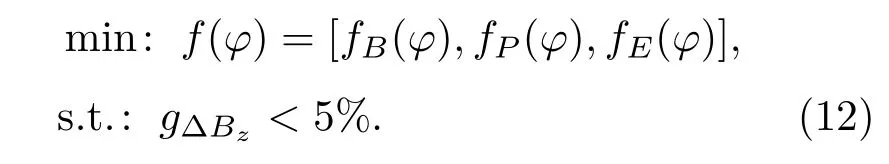
多目标处理方法主要有:全局加权准则法、加权和法、字典式法、加权最小最大法、指数加权法和加权积法等.为了更好地分析各个目标参数,本文采用加权和与归一化相结合的多目标处理方法［24,25],其表达形式为

ωB,ωP,ωE分别是目标函数fB,fP,fE的对应权重系数.

2.3.3 敏度分析

在优化过程中,需要计算函数的敏度:

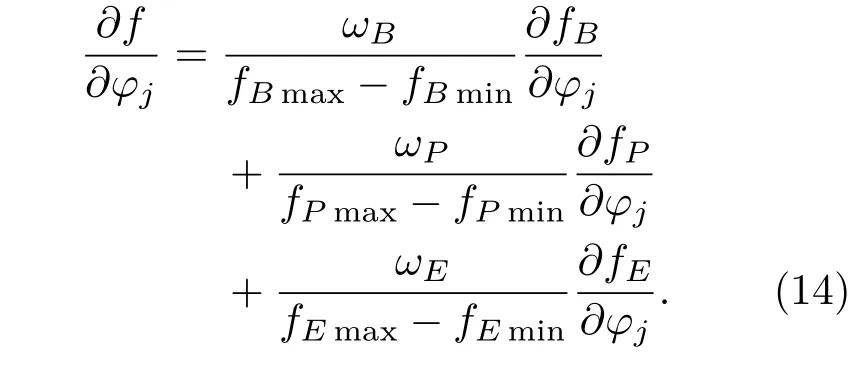
根据(2)和(4)式可求出线性度函数fB的敏度:

其中p是ROI离散点的总数.根据(6)式,能耗目标函数的流函数表达形式可写成

对其求敏度

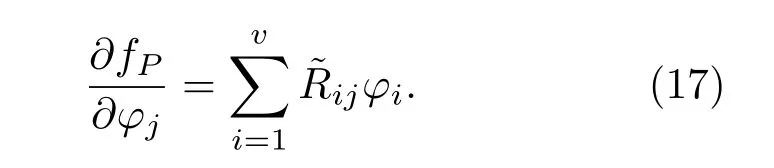
根据(10)式可推出磁场能目标可表示为

对于加权目标f(φ),其敏度可由(14)式计算.

3 算 例

本文以y方向梯度线圈设计为例在超椭圆柱设计表面进行多目标梯度线圈设计.设定ROI磁场强度梯度的目标值

3.1结合磁场能的优化

本小节只讨论磁场能与磁场线性度,故能耗的权重系数ωP取为0,目标函数可表达为

其中ωB+ωE=1.

为方便比较,计算中以优化后的线圈Coil0为参照进行对比,其中Coil0是磁场能权重系数ωE=4.8×10−4时的计算结果,参数如表1所列.

由图2(b)可知在Coil0处有

表1 梯度线圈Coil0参数Table 1.Parameters of the gradient coil,Coil0.

如图2所示,增加磁场能目标的权重值能够有效降低磁场能,但随着磁场能权重系数的增加将导致线性度目标fB的增加,降低了线性度.由(21)式可知在Coil0处磁场能降低1%将导致磁场线性度损失10.11%;然而磁场能与电感呈线性关系,增加磁场能将导致电感增加,进一步会增加磁共振系统的响应时间.因此,在设计中需综合考虑各因素,针对设计需求进行优化设计.

磁场能目标除了能够优化磁场能的大小外,还可以用来优化线圈的设计尺寸.增加ROI的体积将导致磁场能增加.在ROI尺寸不变时,合理地降低线圈分布表面尺寸,将提高磁共振系统的空间利用率,提高磁共振系统的工作效率.在本文中,利用优化磁场能来得到合理的线圈分布表面尺寸.

如图3所示,随着线圈分布表面高度h的增加,线性度与磁场能均减小,在h增加到180 mm时,磁场能与场强线性度趋于平缓;当h增大至400 mm时增加高度会导致磁场能变大而线性度变好.对比图4中在不同高度、相同权重系数下的线圈线型,可以发现降低h会存在线型振荡,线圈局部密集的现象;而h增大至270 mm后继续增加h值获得的梯度线圈线型的高度相同.因此,在后续的计算中,本文都采用h=270 mm设计分析.通过以上分析可以发现结合磁场能目标与线圈的线型可以更好地选取满足设计要求的线圈尺寸参数.

3.2结合能耗的优化

本小节将讨论线圈能耗与磁场线性度对线型的影响,磁场能的权重系数ωE取为0,目标函数可表达为

其中ωB+ωP=1.

图2 (a)归一化fB-fE的Pareto曲线及其(b)对应的偏微分曲线Fig.2.(a)Pareto curve in the normalized fB-fEand(b)corresponding partial di ff erential curve.

图3 设计表面高度h与(a)梯度线圈线性度、(b)磁场能线圈的关系(计算时取ωE=4.8×10−4)Fig.3.The relationship of the height of current-carrying surface to(a)normalized objection fB/fB0and(b)normalized objection fE/fE0(weight parameter:ωE=4.8×10−4).

图4 (a)—(e)h=150,200,270,300和350 mm时的四分之一线型Fig.4.Quadrant of wire paths of gradient coils corresponding to(a)h=150 mm,(b)h=200 mm,(c)h=270 mm,(d)h=300 mm,(e)h=350 mm.

线圈的能耗主要受线圈的长度与电流的大小影响,优化能耗函数,其实质是对线圈线长的约束,使线型规整,减少线型振荡的产生.为方便比较能耗目标对梯度线圈设计的影响,该部分的设计表面都设定为a=45 mm,b=36 mm,h=270 mm.

如图5所示,通过增加能耗目标权重系数可以有效减小梯度线圈的能耗.根据实际对线性度与能耗需求可以选取合适的权重系数,使梯度磁场的线性度控制在合理的范围内.对比图中A,B位置的参数与线型如表2和图6所示,发现增大能耗的权重系数,可以减小线圈电流,同时使线圈更光滑.

图5 磁场线性度与线圈能耗目标值和权重系数的关系Fig.5.The relationship of the weight parameter for power dissipated ωPto objective value for power dissipated fPand objective value for linear gradient deviation fB.

3.3结合能耗、磁场能的多目标优化

在实际应用中,梯度线圈的设计是需要综合考虑多个性能参数的多目标优化问题.本节将讨论综合磁场能、能耗、线性度目标设计梯度线圈,目标函数表达形式为(13)式.

表2 图5中A,B位置梯度线圈的性能参数Table 2.Parameters of gradient coils of coil solutions noted as A,B in Fig.5.

图6 (网刊彩色)(a),(b)分别对于图5中A,B位置的线型;(c),(d)是(a),(b)对应的局部线型Fig.6.(color online)(a)Wire paths and stream function of coil solutions noted as A in Fig.5,and(c)part of wire paths corresponding to(a);(b)wire paths and stream function of coil solutions noted as B in Fig.5,and(d)part of wire paths corresponding to(b).

图7 (网刊彩色)Pareto解空间(满足gΔBz≤ 5%,fE≤ 1.25×10−4,fP≤ 0.105),其中(a),(b),(c)分别是对应fP,fE,fB的值Fig.7.(color online)Pareto front solution of multiple objectives optimization problem de fi ned by the objectives fB,fE,fP,and constrained to gΔBz≤ 5%,fE≤ 1.25×10−4,fP≤ 0.105:(a)corresponding to fP,(b)corresponding to fE,(c)corresponding to fB.

表3 图7(c)中C,D,E位置Pareto优化解对应梯度线圈的参数Table 3.Parameters of gradient coils of Pareto front solutions noted as C,D,E in Fig.7(c).

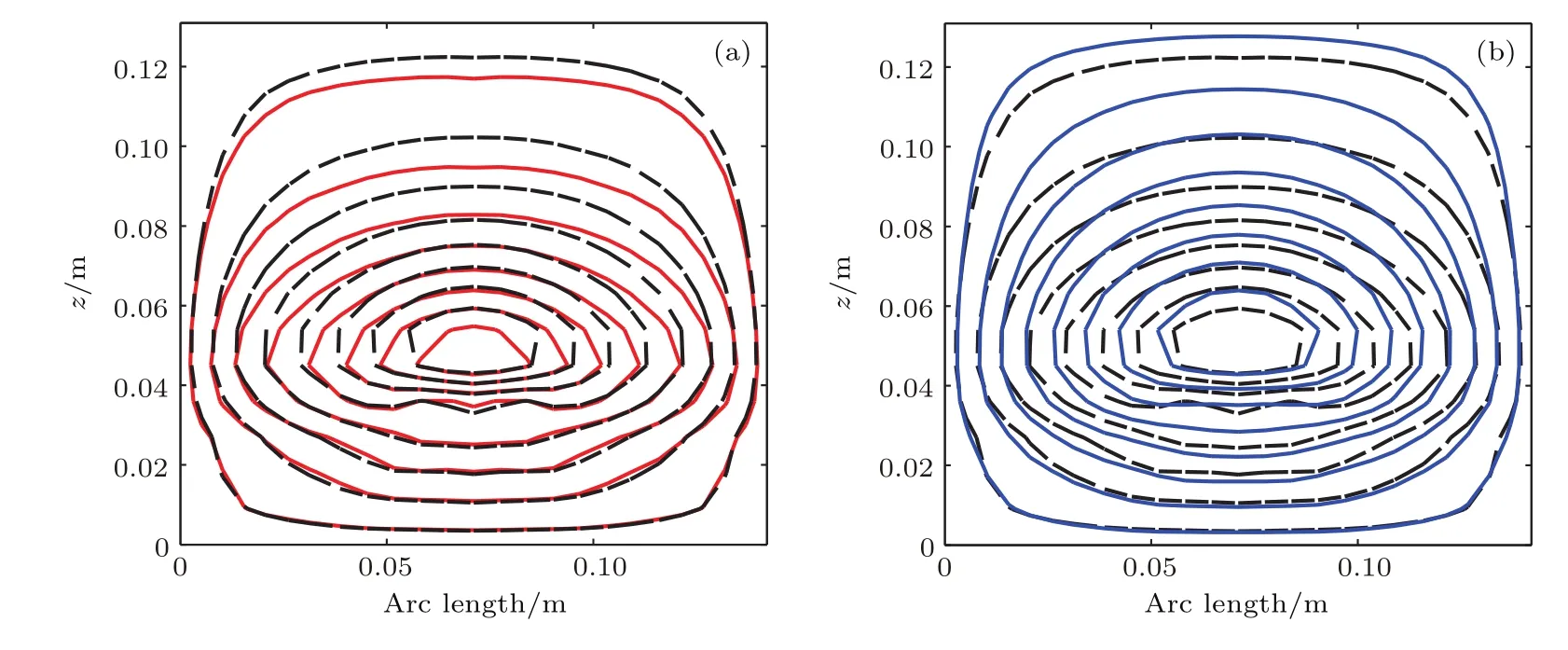
图8 (网刊彩色)图7中C,D,E位置线型比较(黑色虚线是D点的线型,蓝色是E点的线型,红色是C点的线型)Fig.8.(color online)Quadrant of wire paths of gradient coils of Pareto front solutions noted as C,D,E inFig.7(c):(a)coil solutions noted as C(in red solid line),coil solutions noted as D(in black dotted line),(b)coil solutions noted as D(in black dotted line),coil solutions noted as E(in blue solid line).

图7中三角形区域是满足gΔBz≤5%,fP≤1.25×10−4,fE≤ 0.105的Pareto解空间.通过比较图7(a)—(c)的变化趋势,根据实际需求可以直观地得到可行解.表3为图7(c)中C,D,E位置Pareto优化解对应梯度线圈的参数.比较图8中的线型可以发现增加能耗或磁场能的权重将会有效抑制线圈的局部振荡.

4 结 论

梯度线圈的设计是一个多目标优化问题,需要权衡各性能指标,如能耗、磁场能、线性度等.在形状设计时也需要考虑磁场能等目标来达到最佳线圈尺寸,从而提高磁共振系统的空间利用率和工作效率.在实际设计过程中,针对不同的应用需求,需要性能不同的线圈.本文尝试利用多目标优化方法实现超椭圆柱设计表面梯度线圈的设计问题.通过计算表明该方法可以直观地反映多个性能参数的关系,从而在设计过程中根据需求更好地权衡各个参数.从多目标优化设计模型的角度考虑,文中采用的算法可以扩展到多于四个合理目标的线性组合.但是局部最优解的存在与否强烈依赖于各个单目标约束值的选取.如果约束选取的过紧,非常有可能发生可行解不存在的情况.因此,Pareto算法仅仅给出了一个寻找多目标(尤其是多目标之间有冲突的情况下)优化解的一个寻优策略,局部最优解的最终确定还是强烈依赖于设计人员对于各单个目标特性了解的基础上对优化参数的调整.文中通过优化磁场能目标实现了线圈设计表面尺寸的优化,再通过对比能耗、磁场能、线性度目标的变化趋势来设计出满足需求的梯度线圈.其他目标如振动、主动屏蔽等将在后续研究中进一步探讨.

[1]Zu D L 2004Magnetic Resonance Imaging(Beijing:Higher Education Press)pp53–82(in Chinese)[俎栋林2004核磁共振成像学(北京:高等教育出版社)第53—82页]

[2]Wang L,Cao Y H,Jia F,Liu Z Y 2014Acta Phys.Sin.63 238301(in Chinese)[王亮,曹英晖,贾峰,刘震宇2014物理学报63 238301]

[3]Turner R 1986J.Phys.D:Appl.Phys.19 147

[4]Turner R 1988J.Phys.E:Sci.Instrum.21 948

[5]Forbes L K,Crozier S 2002J.Phys.D:Appl.Phys.35 839

[6]Liu W T,Zu D L,Tang X 2010Chin.Phys.B19 018701

[7]Forbes L K,Brideson M A,Crozier S 2005IEEE Trans.Magn.41 2134

[8]Liu W T,Zu D L,Tang X,Guo H 2007J.Phys.D:Appl.Phys.40 4418

[9]Li X,Xie D X,Wang J M 2009IEEE Trans.Magn.45 1804

[10]Tomasi D 2001Magn.Reson.Med.45 505

[11]Peeren G N 2003J.Comput.Phys.191 305

[12]Lemdiasov R A,Ludwig R 2005Concepts Magn.Reson.B:Magn.Reson.Eng.26B 67

[13]Liu Z Y,Jia F,Hennig J,Korvink J G 2012IEEE Trans.Magn.48 1179

[14]Wang Q L 2013Practical Design of Magnetostatic Structure Using Numerical Simulation(Singapore:John Wiley&Sons)pp39–142

[15]Hu G L,Ni Z P,Wang Q L 2012IEEE Trans.Appl.Supercond.22 4900604

[16]Zhu X C,Wang Q L,Wang H S 2016Adv.Technol.Electral.Eng.Energ.35 43(in Chinese)[朱旭晨,王秋良,王厚生2016电工电能技术35 43]

[17]Li X,Xia L,Chen W F,Liu F,Crozier S,Xie D X 2011J.Magn.Reson.208 148

[18]Hu Y,Wang Q L,Li Y,Zhu X C,Niu C Q 2016Acta Phys.Sin.65 218301(in Chinese)[胡洋,王秋良,李毅,朱旭晨,牛超群2016物理学报65 218301]

[19]Turner R 1993Magn.Reson.Imag.11 903

[20]Abduljalil A M,Aletras A H,Robilaille P M L 1994Magn.Reson.Med.31 450

[21]Alsop D C,Connick T J 1996Magn.Reson.Med.35 875

[22]Pissanetzky S 1992Meas.Sci.Technol.3 667

[23]Bowtell R,Robyr P 1998J.Magn.Reson.131 286

[24]Wang L Q,Wang W M 2014Chin.Phys.B23 028703

[25]Sanchez C C,Pantoja M F,Poole M,Bretones A R 2012IEEE Trans.Magn.48 1967

[26]Marler R T,Arora J S 2004Struct.Multid.Optim.26 369

[27]Marler R T,Arora J S 2005Eng.Optim.37 551

[28]Xie D X,Sun X W,Bai B D,Yang S Y 2008IEEE Trans.Magn.44 1006

PACS:83.85.Fg,02.60.Cb,87.55.de,45.10.DbDOI:10.7498/aps.66.098301

Design of super-elliptical gradient coils based on multiple objective Pareto optimization method∗

Pan Hui1)2)Wang Liang1)Wang Qiang-Long1)Chen Li-Min1)2)Jia Feng3)Liu Zhen-Yu1)†

1)(Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)2)(University of Chinese Academy of Sciences,Beijing 100039,China)3)(Department of Radiology,Medical Physics,Medical Center University of Freiburg,Faculty of Medicine,University of Freiburg,Freiburg 79110,Germany)

21 December 2016;revised manuscript

6 February 2017)

The design of gradient coils for a magnetic resonance imaging(MRI)system is a multiple objective optimization problem,which usually needs to deal with a couple of con fl icting design objectives,such as the stored magnetic energy,power consumption,and target linear gradient distribution.These design requirements usually con fl ict with each other,and there is no unique optimal solution which is capable of minimizing all objectives simultaneously.Therefore,the design of gradient coils needs to be optimized reasonably with the tradeo ffamong di ff erent design objectives.Based on the developable property of the super-elliptical cylindrical surface and the stream function design method,the multiple objective optimization problem is analyzed by using the Pareto optimization method in this paper.The e ff ect of proposed approach is illustrated by using the stream function method and three aforementioned coil design objectives are analyzed.The in fl uences of the stored magnetic energy and power consumption target on linearity of gradient coil and the con fi guration of coils are analyzed respectively.The suitable sizes of gradient coils are discussed by analyzing the change of the stored magnetic energy.A weighted sum method is employed to produce the optimal Pareto solutions,in which the multiple objective problem reduces into a single objective function through a weighted sum of all objectives.The quantitative relationship of each design requirement is analyzed in the Pareto solution space,where Pareto optimal solutions can be intuitively found by dealing efficiently with the tradeo ffamong di ff erent coil properties.Numerical examples of super-elliptical gradient coil solutions are provided to demonstrate the e ff ectiveness and versatility of the proposed method to design super-elliptical gradient coils with di ff erent coil requirements.The optimization results show that there are multiple available solutions in the convex Pareto solution space under the constraints that the linear gradient deviation is less than 5%and the magnetic stored energy and power dissipated are both no more than user-preset values.In the case that the values of summed objective functions are the same,the proposed method can intuitively see the performance of each individual target,thereby conducting to realizing the fi nal design of gradient coils under the di ff erent design requirements.With the proposed approach,coil designers can have a reasonable overview of gradient coil design about the achievable performances of some speci fi c properties and the competing or compatible relationships among coils properties.Therefore,a suitable design of the gradient coils for a given requirement of MRI application can be chosen reasonably.

gradient coils,stream function,super-elliptical cylindrical surface,Pareto optimization

10.7498/aps.66.098301

∗国家自然科学基金(批准号:51675506,51275504)、吉林省科技发展计划(批准号:20140519007JH)和欧洲研究理事会ERC启动基金RANGEmri 282345项目资助的课题.

†通信作者.E-mail:liuzy@ciomp.ac.cn

*Project supported by the National Natural Science Foundation of China(Grant Nos.51675506,51275504),the Science and Technology Development Plan of Jilin Province,China(Grant No.20140519007JH),and an European Research Council Starting Grant ‘RANGEmri’(Grant Agreement 282345).

†Corresponding author.E-mail:liuzy@ciomp.ac.cn