星载多角度偏振成像仪非偏通道全视场偏振效应测量及误差分析∗

钱鸿鹄 孟炳寰 袁银麟 洪津 张苗苗 李双 裘桢炜

1)(中国科学院安徽光学精密机械研究所,合肥 230031)

2)(中国科学技术大学,合肥 230026)

3)(中国科学院通用光学定标与表征技术重点实验室,合肥 230031)

星载多角度偏振成像仪非偏通道全视场偏振效应测量及误差分析∗

钱鸿鹄1)2)3)†孟炳寰1)3)‡袁银麟1)3)洪津1)3)张苗苗1)2)3)李双1)3)裘桢炜1)3)

1)(中国科学院安徽光学精密机械研究所,合肥 230031)

2)(中国科学技术大学,合肥 230026)

3)(中国科学院通用光学定标与表征技术重点实验室,合肥 230031)

(2016年12月27日收到;2017年2月9日收到修改稿)

星载多角度偏振成像仪自身的光学系统有一定的偏振效应,会影响非偏通道的辐射测量精度.斜入射到光学元件上的光透射率是偏振敏感的,导致了光学系统的线偏振效应.为精确反演解析出观测目标光的辐射强度,需对成型仪器本身的偏振效应进行准确的测量、定标、校正.通过分析仪器原理和光路结构,详细推导出仪器非偏通道含线偏振效应的辐射测量模型,并根据实际镜头特点合理简化了模型.提出了基于不同偏振角的完全线偏光在仪器全视场内稀疏入射并最小二乘拟合响应值的方法,对非偏通道全视场线偏振效应进行测量和定标,同时对此方法的定标过程进行了仿真.另外,分析了仪器主要物理参数有偏差时对不同偏振态入射光的反演误差,如仪器单像元方位角、显式起偏效应、低频透过率.对仪器开展了实验室定标实验,得到了仪器主要物理参数范围及其拟合偏差量,进一步算出显式起偏效应参数偏差引起的辐射定标强度相对误差最大为0.4%,满足仪器辐射精度5%的要求并留足余量.该研究为仪器非偏通道全视场的高精度辐射测量、定标及后期数据处理提供了理论依据及实验指导.

∶辐射测量精度,偏振效应,大视场,Stokes-Mueller矩阵

PACS∶07.07.Df,07.05.Tp,42.25.Ja,42.30.—dDOI∶10.7498/aps.66.100701

1 引 言

星载多角度偏振成像仪(spaceborne directional polarimetric camera,DPC)[1]是由中国科学院安徽光学精密机械研究所设计并研制的一种超广角画幅式低畸变成像航天遥感偏振传感器,可以获取大气气溶胶及云的多角度偏振辐射成像信息.辐射测量精度是仪器性能的重要技术指标,对卫星遥感高精度定量参数反演具有重要意义[2].通常星载遥感器本身都会有一定的线偏振效应,有同样辐射强度的不同线偏振态入射光会被测出不同的光强水平.来自地球的反射光通常都是部分线偏振且随机分布,若不能准确量化仪器的线偏振效应,不知道入射光的偏振态,那么在辐射测量数据反演时就不能校正仪器本身的线偏振效应,从而降低应用数据的精度[3,4].

很多星载遥感器都对自身的偏振效应进行了研究[5−8],通常仪器的偏振效应主要由光学系统引起,常见的光学元件如透镜、光栅、反射镜、二向色镜、光纤等在发生反射或透射时都会产生偏振效应[4].所有的这些偏振效应元件耦合在一起最终呈现出整个仪器的偏振效应.为提高DPC对地物目标的辐射测量精度,一方面是在设计阶段就要考虑低水平线偏振效应的仪器光学系统设计,另一方面在仪器已经研制定型的情况下,对其线偏振效应进行精确的测量,为校正提供量化参数,从而提高辐射测量精度.

DPC的超广角镜头是引起仪器线偏振效应的主要因素,国内陈立刚等[9]对航空版DPC的光学偏振特性进行了初步的实验研究,使用大积分球非偏光源充满DPC全视场来研究了仪器偏振通道的全视场光学偏振特性.由于光学镜头镀膜的原因,镜头引起的偏振效应在不同波段间不是缓变的,不能简单地将偏振通道(偏振波段)和非偏通道(非偏波段)的镜头偏振效应参数相互替换或在光谱维上拟合近似推算[3],需要对DPC非偏通道的偏振效应进行专门测量、定标、校正.

在DPC研制成型的情况下,本文根据DPC的原理和光路结构特点,考虑超广角镜头的偏振效应,以Stokes-Mueller矩阵的方式给出了仪器非偏振通道的辐射测量模型,在仪器只具有线偏振探测能力的情况下,科学合理地简化了模型.提出了非偏通道的仪器全视场线偏振效应测量方法,对辐射测量模型进行了仿真,重点分析了仪器像元方位角、显式起偏效应、低频透射率等物理参数的偏差对辐射测量精度的影响.然后开展了具体实验,得到的实验结果验证了此方法可高精度定标出仪器的显式起偏效应,但对于方位角和低频透射率的定标精度较低.另外评估了此一种测量方法定标出三种参数时的辐射定标精度.

2 DPC光学系统

DPC光学系统主要由三部分构成∶超广角像方远心成像物镜、滤光片-偏振片(衰减片)组合转轮、面阵电荷耦合(CCD)探测器[1].沿轨和穿轨方向视场均为100◦,探测器阵列上有效像元数为512×512.转轮共有15个测量通道,设置8个波段,其中3个偏振波段(每个偏振波段有连续3个通道),5个非偏,另外1个本底通道用来测量暗电流.超广角成像物镜是多角度数据观测的实现方式,也是仪器本身偏振效应的主要来源[9,10].

DPC光学镜头共有12片透镜(20个介质面),对于DPC非偏振通道,镜头之后是滤光片+衰减片,最后端是CCD面阵,如图1所示.大视场角入射的光束,与镜头介质表面呈斜入射情况,且有视场角越大斜入射角越大的趋势,这表明了DPC镜头本身量化偏振效应随视场角变化的特点.

图1 (网刊彩色)光学系统特点Fig.1.(color online)Characteristics of the optical system.

3 非偏通道辐射测量模型

根据偏振辐射理论,任何来自目标的辐射光束均可由Stokes矢量描述.在遥感探测中通常假定Stokes矢量S=[I,Q,U,V]T的圆偏振分量V=0[11,12],使用I,Q,U三个分量即可表示光束线偏振信息.其中∶

I表示辐射光总强度,Inp表示非偏辐射强度,Ipol表示偏振辐射强度,χ表示偏振角(angle of linear polarization,AoLP),Ipol/I表示线偏振度(degree of linear polarization,DoLP).DPC是一台线偏振测量仪,不考虑仪器的圆偏特性时,DPC本身对辐射光偏振态的改变可由一个3×3的Mueller矩阵[4,13]描述.

3.1 镜头的Mueller矩阵

假设所有镜片均满足圆对称且装配满足同轴,将镜头作为满足圆对称结构的整体进行研究.通常光学镜头的偏振效应可分为三类[14]∶双向衰减、相位延迟、退偏.由于DPC仪器特点所限——只能探测线偏振,整机情况下无法独立研究相位延迟,同时目标光也只关注线偏振信息.故降维研究线偏振效应时,镜头的3×3本征Mueller矩阵可表示为[15−20]

其中,D和Dv分别是退偏参数和交叉退偏参数,TL是镜头透射率参数,ε=−cos2ψ表示线性起偏效应(双向衰减).

CCD像元阵列的行列方向分别为+X0和+Y0方向,设O-X0Y0为全视场成像坐标系.单像元的子午和弧矢方向分别设为+X和+Y本征坐标系.图2给出了单像元本征坐标系和全视场成像坐标系的关系,其中+X与+X0的夹角(方位角)为ϕ.

图2 全视场成像坐标系、单像元本征坐标系和检偏器振透方向Fig.2.Reference frames and the polarizer direction;(X0,Y0)for the imaging reference frame;(X,Y)for the principal reference frame linked to a single pixel.

其中TF为滤光单元透射率,T为系统总透射率.CCD线性响应时,单像元上的光强转化成显示输出的DN(digital number)值可表示为

其中,G表示CCD电子学增益;t表示CCD电子学曝光时间;A表示对应光谱段的绝对辐射定标系数,单位DN ·W−1·m2·sr·µm ·ms−1;C 表示本底暗电流.

3.2 镜头的退偏D

每个单像元的成像光束都有一定孔径尺寸,这束光在经过镜头结构、透镜面形,会聚成像点时,会引起退偏[3,4,14,17,21,22],(2)式中的D可表征此退偏量.为评估镜头中由于孔径效应引起的退偏量,利用不同偏振角的完全线偏光入射DPC偏振通道进行实验研究.

DPC偏振通道中,镜头后面是转轮中有一定方位角的线偏振片.方位角为0的线偏振片3×3本征Mueller矩阵可表达为

其中TP为线偏振片透射率.图2给出了成像坐标系中线偏振片振透轴方向,与+X0轴的夹角为α.对于各本征坐标系下的入射光束,转轮里的线偏振片有(α−ϕ)的方位角,所以DPC偏振通道的本征Mueller矩阵为

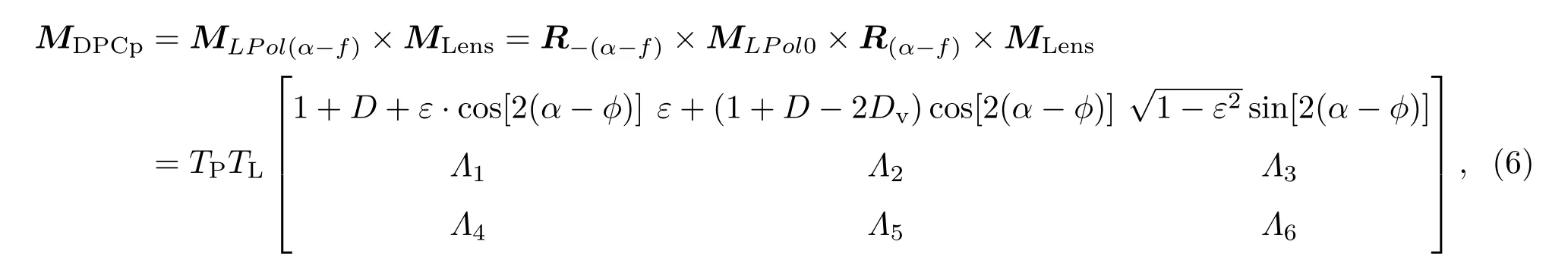
用10◦间隔偏振角的完全线偏光分别从中心和四角共5个典型视场位置入射DPC的865 nm三检偏通道进行实验. 三检偏通道中检偏片的相对方位角(以865P2通道作为0基准)已知,α865P1=−60.13◦,α865P2=0◦,α865P3=59.98◦.实验结果按模型(7)式进行三通道全局最小二乘拟合,得到未知参数,结果如图3和表1所列,其中DC是扣除本底暗电流后的CCD响应值(DN−C).各视场响应拟合匹配度Adj.R-square均接近于1,表明所建模型和拟合出的未知参数值能正确表征仪器实际特性.

图3 (网刊彩色)三检偏通道中心视场单像元响应值及其拟合Fig.3.(color online)Response values andfitting curve of the central view of the three polarized channelof DPC.

表1 三检偏通道中5个视场位置的响应值拟合参数结果Table 1.Fitting parameter results of response values of thefive viewing position of the polarized channel.

由表1可知,中心视场处镜头引起的线性起偏效应和退偏可近似相互抵消,而且退偏在全视场范围内都是一个小量(＜0.02).

3.3 非偏通道全视场辐射测量模型

在仪器已研制固型的状态下,对于DPC非偏通道,为测量定标出仪器本身的全视场偏振效应,在退偏是一个小量的情况下,将线性起偏效应、退偏两种独立效应归为一个综合的偏振效应参数,在此设为显式起偏效应E(无退偏).则DPC非偏通道中单像元的辐射测量模型((4)式)可简化为

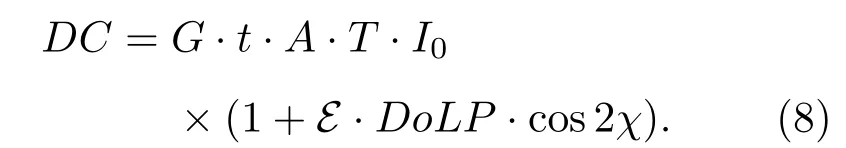
测量定标的难点在于如何确定全视场下各个单像元尺度的透射率、显式起偏效应和方位角.逐个微元独立定标无可操作性,而且DPC实际情况下都是全视场(512×512像元)成像,需将上述单像元辐射测量模型推演到全视场辐射测量模型表达形式.全视场微元的透射、响应差异可归结为空间非均匀性,将其分为两类[5,23]∶

1)空间低频透射率∶(9)式中的P,包含镜头、滤光片/衰减片透射率空间低频差异;

2)空间高频透射率、响应率∶(9)式中的g,主要是CCD像元间的响应率差异.

像元坐标位置直角坐标系(i,j)转换到极坐标系(θ,ϕ),θ表示视场角,ϕ表示方位角,DPC非偏通道的全视场辐射测量模型表示为

其中,DC0表示CCD响应线性区不过零点的截距.标识符含义∶m表示CCD电子学增益档位;s表示CCD电子学积分时间档位;k表示光谱波段(1≤k≤8).

4 非偏通道辐射测量仿真

4.1 全视场辐射测量仿真参数设定

确定DPC中心零视场对应的像元位置坐标,以各个像元位置坐标到零视场坐标的距离(radius)作为视场角(θ)的对应量.根据文献[6,9]的研究结果,将模型中各物理参量设定如表2所列(暂不考虑CCD高频响应差异).

表2 非偏通道全视场辐射测量仿真参数设定值Table 2.Setting values of some important parameters.

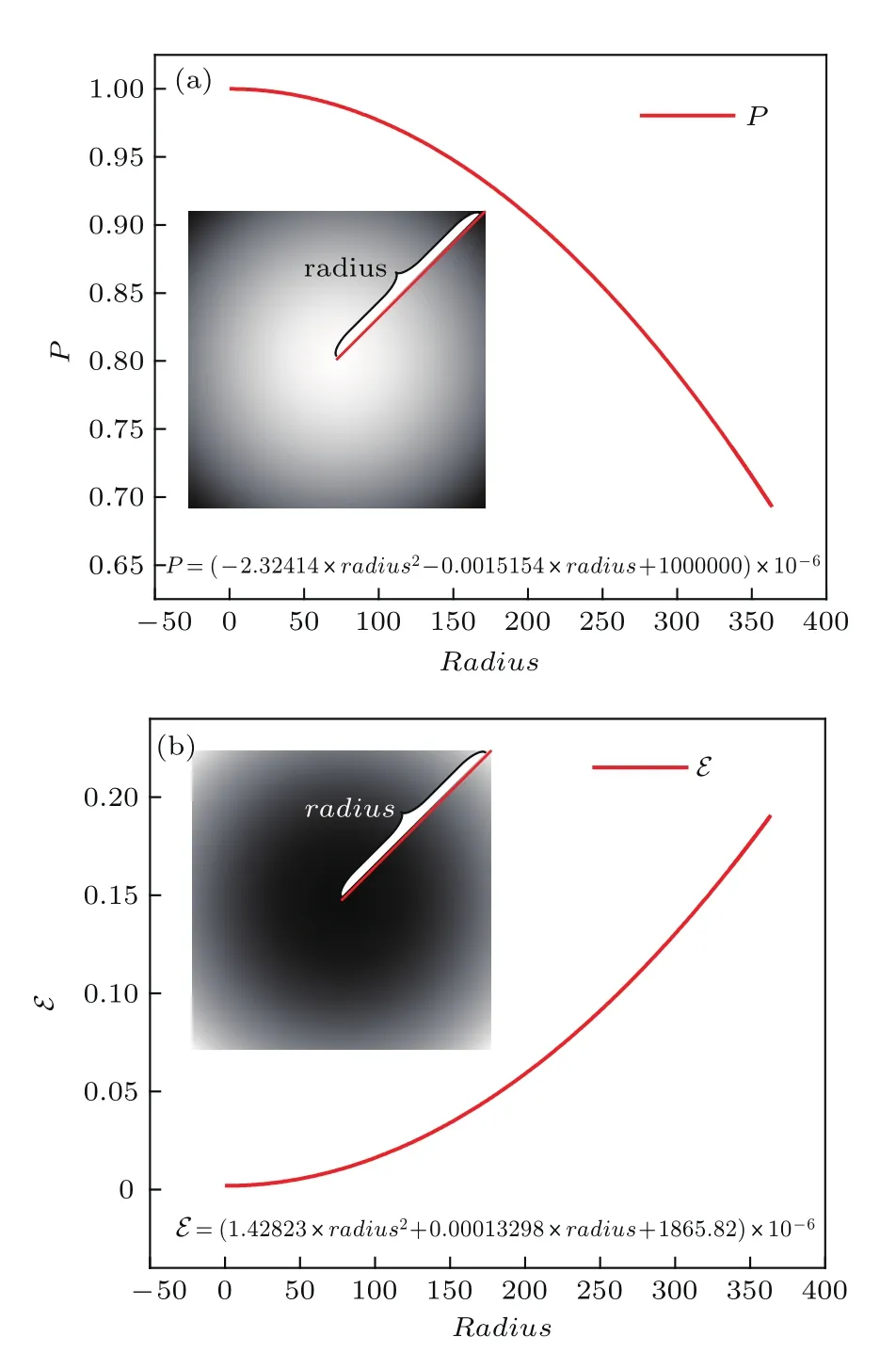
图4 全视场低频相对透射率P、显式起偏效应E随radius的变化关系设定及二维示意Fig.4.Typical shapes and setting values for the polynomial P and E as a function of the radius.

图4表示P,E的二维矩阵设定值,满足圆对称,并给出了径向方向的数学模型.完全线偏光入射DPC非偏通道时,单像元测量响应模型是∶

其中,Z=G ·t·A·g ·P ·I0,χ0是初始方位角.

4.2 完全线偏光入射仿真

实验室条件下,满足DPC全视场如此大面积的均一线偏光源几乎是不存在的,所以每次只选取单个分视场(如单像元)进行仿真.图5给出了第162行、第458列的单像元在本征坐标系下对不同偏振角的完全线偏光入射的响应值,其中红线是按(10)式模型进行最小二乘拟合的结果,周期定为180◦,线性响应的截距定为0,得到未知参量Z,E,χ0的数值.

图5 不同偏振角完全线偏光入射非偏通道单像元仿真响应及拟合Fig.5.Simulate response values andfitting curve of a single pixelof the non-polarized channelof DPC.

所以,在全视场成像坐标系中,用不同偏振角的完全线偏光在DPC全视场内稀疏分视场入射+最小二乘拟合的方法可以定标出DPC非偏通道分视场空间低频透射率P、显式起偏效应E、单像元方位角ϕ,由于这三项参数均是低频缓变量,然后再用多项式函数或线性函数拟合出全视场定标值.

4.3 反演仿真及误差

最小二乘方法拟合时,Z,E,χ0都是未知量,拟合值均会有一定误差,而且再次进行全视场低频拟合时也会有误差.对应到仪器全视场空间低频相对透射率P、显式起偏效应E和单像元方位角ϕ定标误差,则解析出的辐射强度测量值为

其中DoLPin表示入射光的偏振度,χin表示全视场成像坐标系下入射光的偏振角,参量上带横线表示仪器参数定标值.由的定标值误差引起的辐射强度测量相对误差是∶

由3.1和4.1节知,DPC非偏通道满足圆对称情况下,P随视场角增大而减小的同时,E随视场角增大而增大,且有一一对应关系,故可将P和E的值联动设置来进行误差分析.

图6(a)—(c)给出了入射光本征偏振角χ=130◦时,三种仪器偏差(δP,δE,δϕ)的反演仿真情况,图6(d)—(f)给出了入射光DoLPin=1时,三种仪器偏差(δP,δE,δϕ)的反演仿真情况.

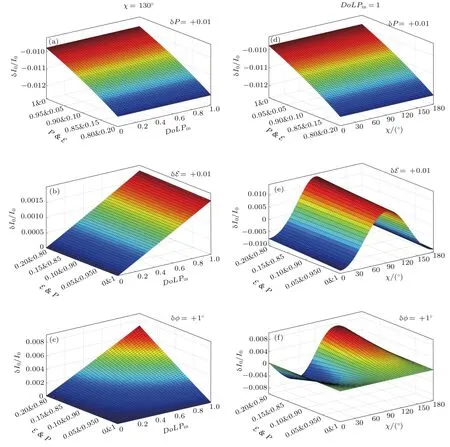
图6 (网刊彩色)仪器参量有偏差时辐射测量强度的相对误差Fig.6.(color online)Relative measurement errors of I0with the P,E of DPC and DoLPinor χ of the incident light when P or E or ϕ deviate.

由上述分析可知∶1)辐射测量强度相对误差是随入射光偏振度(0—1)的增大而增大,在DoLPin=1时达到最大;2)仪器参量P有偏差时,最敏感辐射测量强度相对误差在P&E为0.8&0.2处,与入射光偏振度、偏振角无关;3)仪器参量E有偏差时,误差最敏感在E&P为0.2&0.8、入射光本征偏振角χ为90◦处;4)仪器参量ϕ有偏差时,误差最敏感在E&P为0.2&0.8、入射光本征偏振角χ为130◦处.可以发现,仪器边缘视场角处的辐射测量误差最敏感.

5 实验结果与分析

根据上述定标方法,使用积分球辐射源+旋转偏振片作为定标光源对DPC初样鉴定产品非偏通道进行实验.图7为实验现场,DPC放置在电控二维旋转台上,使得定标光源可以从不同角度入射DPC.图8(a)是51种不同入射角度的成像光斑合成图,其中每个光斑均有19种偏振角(间隔10◦)的完全线偏光入射响应,图8(b)就是第247行、第494列单像元的结果.

图9给出了各个稀疏光斑拟合得到的Z,E,χ0值,可分别表示仪器相应入射角度下的空间相对透射率、显式起偏效应、单像元方位角(子午面方位角).中心零视场对应的像元位置在第247行、第261列,设仪器非偏通道是圆对称,空间相对透射率、显式起偏效应只和径向距离(视场角)有关,用多项式函数在空间维再次进行拟合,得到各个单像元的相应参量值,结果如图9所示.另外,单像元方位角用线性函数在空间维拟合.

图9(a)中数据归一化后表征仪器全视场空间低频相对透射率P,图9(c)的χ0和ϕ等价,表3给出了DPC仪器三种参数有独立偏差的具体结果.

图7 (网刊彩色)DPC非偏通道偏振效应定标实验现场Fig.7.(color online)Calibration experiment field of the polarization effects of the non-polarized channelof DPC.

图8 (a)光斑全视场合成图;(b)单光斑对不同偏振角完全线偏光的响应值及其拟合Fig.8.(a)Composite map of full field of light spots;(b)response values andfitting curve of different kind of AoLP of incident light in a single spot.

图9 非偏通道(910 nm)径向视场角下的Z,E,χ0结果及其拟合Fig.9.The principle parameters Z,E and χ0calibration values andfitting curve of different views of radial direction of the non-polarization channel(910 nm).

表3 仪器主要参数偏差及辐射定标强度最大相对误差Table 3.The max radiometric calibration relative errors due to deviations of three kinds of parameters.

合成后最大相对误差为∶δI0/I0=这就是用此种定标方法同时定出非偏通道三种仪器参数的辐射定标精度.

6 结 论

本文通过分析DPC光学系统的特点,推导出仪器非偏通道含线偏振效应的辐射测量模型,通过实验研究忽略退偏,使用一种显式起偏效应参数来综合表征镜头的偏振效应,合理简化了模型.提出用不同偏振角的完全线偏光在DPC非偏通道全视场内稀疏分视场入射+最小二乘拟合的定标方法,得到空间低频透射率P、显式起偏效应E、单像元方位角ϕ这三项仪器参数,并进行了误差仿真分析和实验,结果表明单项参数显式起偏效应E的定标值引起的DPC非偏通道辐射定标精度可达0.4%,完全满足辐射定标总精度5%[6,24,25]的要求,为仪器此项参数的定标提供了理论依据及切实可行的实验指导.此方法同时还得到其他两种精度较低的仪器参数(P是1.93%,ϕ是0.95%),不建议用于正式定标,这也表明通常一种定标方法只适宜定一种参数,不同参数需要根据其各自特点设计不同的定标方法.此非偏通道偏振效应的研究对提高常规广角透射成像遥感器辐射测量精度同样具有一定的适用性.

另外,本方法是在实验室内入射光偏振态已知的前提下进行的误差分析,若DPC实际在轨运行时,获取的目标偏振态也有误差,根据(11)式,将DoLPin误差耦合进显式起偏效应,重新计算精度即可,这也体现出在轨偏振态波段间定标的必要性[5,8,23].

[1]Yang W F,Hong J,Qiao Y L 2015 Acta Opt.Sin.35 0822005(in Chinese)[杨伟锋,洪津,乔延利 2015光学学报35 0822005]

[2]Diner D J,Chipman R A,Beaudey N,Cairns B,Foo L D,Macenka S A,Cunningham T J,Seshadri S,Keller C U 2005 Proc.SPIE 5659 88

[3]Waluschka E,Silverglate P,Ftaclas C,Turner A 1992 Proc.SPIE 1746 96

[4]Maymon P W,Chipman R A 1992 Proc.SPIE 1746 148

[5]Hagolle O,Goloub P,Deschamps P Y,Cosnefroy H,Herman M 1999 IEEE Trans.Geosci.Remote Sensing 37 1550

[6]Bret-Dibat T,Andre Y,Laherrere J M 1995 Proc.SPIE 2553 218

[7]Goloub P,Toubbe B,Herman M,Bailleul T,Hagolle O,Martinuzzi J M,Rouge B 1997 Proc.SPIE 2957 299

[8]Hagolle O,Guerry A,Cunin L,Millet B,Perbos J,Laherrère J M,Bret-Dibat T,Poutier L 1996 Proc.SPIE 2758 308

[9]Chen L G,MengfG,Yuan Y L,Zheng X B 2011 J.Optoelectron·Laser 22 1629(in Chinese)[陈立刚,孟凡刚,袁银麟,郑小兵2011光电子22 1629]

[10]Sen A K,Kakati M 1997 Astron.Astrophys.Suppl.Ser.126 113

[11]Hou J F,Wu T X,Wang D G,Deng Y Y,Zhang Z Y,Sun Y Z 2015 Acta Phys.Sin.64 060701(in Chinese)[侯俊峰,吴太夏,王东光,邓元勇,张志勇,孙英姿2015物理学报64 060701]

[12]Leroy M,Deuze,BreonfM,Hautecoeur O,Herman M,Buriez J C,Tanre D,Bouffies S,Chazette P,Roujean J L 1997 J.Geophys.Res.102 17023

[13]Chen L G,MengfG,Yuan Y L,Zheng X B 2010 J.Atmosph.Environ.Opt.5 227(in Chinese)[陈立刚,孟凡刚,袁银麟,郑小兵2010大气与环境光学学报5 227]

[14]Chipman R A 1999 Proc.SPIE 3754 14

[15]Nee S Mf2003 J.Opt.Soc.Am.A 20 1651

[16]Nee S M F,Yoo C,Cole T,Burge D 1998 Appl.Opt.37 54

[17]Nee S Mf2006 Appl.Opt.45 6497

[18]Qiu Z W,Hong J 2014 Infrared Laser Eng.43 806(in Chinese)[裘桢炜,洪津2014红外与激光工程43 806]

[19]Chen L G 2008 Ph.D.Dissertation(Beijing:Graduate University of Chinese Academy of Sciences)(in Chinese)[陈立刚2008博士学位论文(北京:中国科学院研究生院)]

[20]Shintani R,Fan A Y,Kang C H 1994 Polarized Light(Beijing:Atomic Energy Press)pp60–71(in Chinese)[新谷隆一,范爱英,康昌鹤1994偏振光(北京:原子能出版社)第60—71页]

[21]Chipman R A 1989 Opt.Eng.28 0290

[22]Chipman R A 2005 Appl.Opt.44 2490

[23]Fougnie B,Bracco G,Lafrance B,Ruffel C,Hagolle O,Tinel C 2007 Appl.Opt.46 5435

[24]Sakuma F,Bret-Dibat T,Sakate H,Ono A,Perbos J,Martinuzzi J M,Imaoka K,Oaku H,Moriyama T,Miyachi Y,Tange Y 1995 Proc.SPIE 2553 232

[25]Andre Y,Laherrere J M,Bret-Dibat T,Jouret M,Martinuzzi J M,Perbos J 1995 Proc.SPIE 2572 79

PACS∶07.07.Df,07.05.Tp,42.25.Ja,42.30.—dDOI∶10.7498/aps.66.100701

*Project supported by the National Natural Science Foundation of China(Grant No.41405037),and the Astronomical Joint Funds of the Chinese Academy of Sciences,China(Grant No.U1331111).

†Corresponding author.E-mail:honghu@mail.ustc.edu.cn

‡Corresponding author.E-mail:bhmeng@aiofm.ac.cn

Full field of view polarization effect measurement and error analysis of non-polarized channels of spaceborne directional polarimetric camera∗

Qian Hong-Hu1)2)3)†Meng Bing-Huan1)3)‡Yuan Yin-Lin1)3)Hong Jin1)3)Zhang Miao-Miao1)2)3)Li Shuang1)3)Qiu Zhen-Wei1)3)
1)(Anhui Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Hefei 230031,China)
2)(University of Science and Technology of China,Hefei 230026,China)
3)(Key Laboratory of Optical Calibration and Characterization,Chinese Academy of Sciences,Hefei 230031,China)

27 December 2016;revised manuscript

9 February 2017)

The optical system of spaceborne directional polarimetric camera that employs an ultra wide-angle lens for its multiangle,afilter wheel for its multispectral and also its multipolarization capability,a CCD itself for its imaging has a certain polarization effect,which can affect the radiometric accuracy of the non-polarized channels of the instrument.The transmittance of the oblique light rays that are incident on the optical element surfaces is sensitive to the orientation of the electric field,contributing to the linear polarization effect of optical system.The precise polarization measurement and calibration of the passive imaging polarimetry are in urgent need to eliminate the instrumental polarization effect and to improve its radiometric accuracy for observation scenes.The non-polarized channel radiometric model considering the linear polarization effect is deduced in detail by analyzing the instrumental principle and optical structures.Moreover,the reasonably simplified model is established based on the actual lens characteristics.A calibration method in which completely linearly polarized light with different kinds of polarization angles irradiates sparsely the instrument within full field of view and subsequentlyfits the response in the least square sense,is proposed and simulated.In addition,the measured relative errors of the intensity of incident light with different kinds of polarization states caused by the calibration deviations of instrumental principal physical parameters are analyzed and calculated,such as the azimuthal angle of single pixels,explicit optic polarization rate and low frequency spatial relative transmittance.The actual instrumental parameter values and their calibration deviation amounts are acquired by carrying out the laboratory calibration experiment for instrument and combining the least squarefitting.Furthermore,the maximum radiometric calibration relative error caused by the deviation of the physical parameter called explicit optic polarization rate is calculated to be 0.4%,fulfilling completely the requirement of radiometric relative accuracy 5%and retaining abundant tolerance.The study provides a theoretical basis and an experimental guidance in high accurately measuring radiation,calibrating and processing data for the instrumental non-polarized channels with full field of view.

∶radiometric accuracy,polarization effect,wide field of view,Stokes-Mueller

∗国家自然科学基金(批准号:41405037)和中国科学院天文联合基金(批准号:U1331111)资助的课题.

†通信作者.E-mail:honghu@mail.ustc.edu.cn

‡通信作者.E-mail:bhmeng@aiofm.ac.cn

©2017中国物理学会Chinese Physical Society

book=100240,ebook=47