一种广义三模腔光机械系统的相干完美吸收与透射∗

张永棠

(广东东软学院计算机科学与技术系,佛山 528225)

一种广义三模腔光机械系统的相干完美吸收与透射∗

张永棠†

(广东东软学院计算机科学与技术系,佛山 528225)

(2016年12月14日收到;2017年3月1日收到修改稿)

提出了一种广义的三模式腔光机械系统,系统的中间是一个反射率为100%的可移动的全反射机械振子,两侧均由一个部分透射的固定光学腔镜构成.其中两个光学腔由一束较强的控制场和一束较弱的信号场驱动与同一个机械振子实现耦合.较弱的信号场将会被该系统完全吸收而不产生任何能量输出,并且当相干完美吸收产生时,输入信号场的能量将由两个腔场和机械模共同分担;较弱的输入信号场由一个腔完美透视到另一个腔而不产生任何的能量损耗.分析与数值结果显示,在不同参数机制下,在该三模光机械系统中可以实现相干完美吸收、相干完美透射和相干完美合成的量子现象.此外,改变腔与腔之间的耦合度,可以实现输出探测场在相干完美吸收和相干完美透射之间转换;通过简单的相位调制,可以实现探测场左腔-右腔的输出和输入方向的互换.这些动态控制在量子信息网络可用来构造光子开关、光子路由、光子交换机等一些特殊功能的光子学器件.

∶物理特性,腔光机械系统,量子光学,光通信

PACS∶71.15.Mb,78.20.Ci,42.55.—f,42.55.WdDOI∶10.7498/aps.66.107101

1 引 言

由于纳米物理和量子光学的快速发展,腔光力学的物理特性以及光机械器件上的应用备受研究者关注.在光机械系统的研究中,一系列很显著的现象,包括光学模式[1]与机械模式[2]的强耦合现象、光机械诱导透明[3,4]以及光学模式与机械模式的相干互换现象[5,6]相继被发现.基于这些现象,可以实现量子信息协议和宏观量子相干,尤其对于复合量子系统在实验及应用方面上实现指明了一个可行的方向.与此同时,把机械振子冷却到基态也在实验上得到证实[7,8],为量子机制下实现对微观尺度机械振子的控制铺平了道路.最近,一个与电磁诱导透明相反的现象,称之为相干完美吸收[9],也在光机械系统中被理论证实[10].然而,目前大部分典型腔光机械系统仍然处于两个自由度之间的耦合,即单个光学模式与单个机械模式的耦合[11].超过两个自由度耦合的多模腔光机械系统[12]却较少受到研究者所关注.

多模腔光机械系统,由于其对深入研究光机械和在量子信息上的潜在应用而逐渐成为一个研究趋势.三模式光机械耦合是一个典型的多模式系统,它包括两个光学腔模或者两个微波腔模与单个机械振子耦合[13]、一个机械模式与一个超导微波腔和一个光学腔耦合[14]以及把一个振动薄膜插入到一个光学腔中构成一个三模式光机械系统[15].基于这些三模式系统,多粒子纠缠[16]、量子态转移[17]、相干光学波长的转换[18]、光学暗态模[19]以及声子调制的电磁诱导吸收等[20]现象相继在理论上被发现.最近,Agarwal和Huang在双腔光机械系统中理论证明了相干完美吸收、相干完美透射以及合成现象[21,22].但是,在多模光机械系统中,现有文献考虑腔与腔之间耦合的研究非常少见.

本文研究了中间振子为全反射、两侧均有控制场和探测场输入的双腔光机械模型,并在双腔光机械模型中提出相干完美透射以及相干完美合成的概念.设计了一种广义的三模耦合光机械系统,实现两个光学腔模或微波腔模与一个机械振子耦合.当分别对这两个光腔施加一个较强的控制场和一个较弱的信号场时,在不同参数机制下,本文设计的三模光机械系统实现了相干完美吸收、相干完美透射和相干完美合成等量子相干现象.并且,可以通过调节系统参数来设定特定频率的探测场.当相干完美吸收产生时,输入的信号场能量完全转化为内腔场的能量和振子的内部相干振动,满足能量守恒定律.当相干完美透射产生时,由于中间机械振子的弛豫速率非常小,保证从系统一侧输入的探测场在不损失能量的情况下从另外一侧完全透射出来.并且中间力学振子的弛豫速率可以保证在一侧的探测场发生完美透射的同时另外一侧的探测场发生全反射,实现相干完美合成.

这些动态控制在量子信息网络中是非常重要的,我们可以设计一个可调节的多模光机械系统,进而实现如光子开关、光子路由、光子交换等全光学控制光子器件在量子信息处理方面的应用.

2 理论模型与计算

本文设计了如图1所示的三模光机械系统,系统中间是一个反射率为100%的可移动的全反射机械振子,两侧均由一个部分透射的固定光学腔镜构成.实现两个光学模或者微波模腔与一个机械振子相耦合.

图1 (网刊彩色)两个被抽运光和探测光驱动的腔与同一个机械振子相耦合的双腔光机械示意图Fig.1.(color online)Schematic of the proposed double cavity opt mechanics where cavity with a strong control field and a weak signal field is coupled to the same mechanical resonator.

三模光机械系统的哈密顿量[18]为

其中,∆k=ωk−ωc是腔肠与控制场之间的失谐;δ=ωs−ωc是信号场与控制场之间的失谐;bin是机械振子的热噪声,ain,k是两个腔的输入真空噪声,它们的平均值为零.

在强驱动场的条件下,算符ak和b可以写成平均值与小的涨落之和∶O=O0+δO(O=a1,a2,b),并且|O0|≫δO.平均值满足如下方程∶

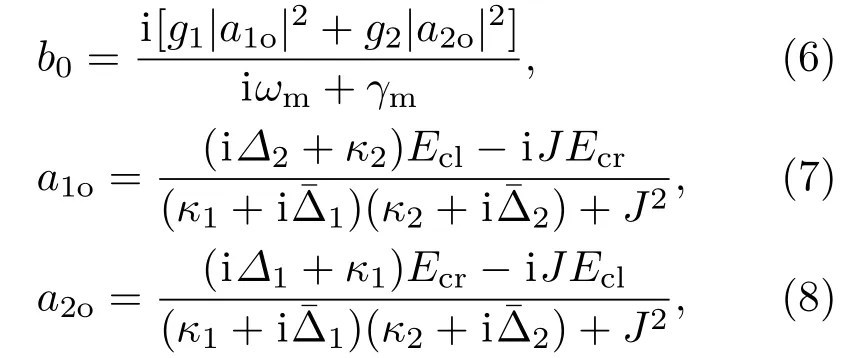
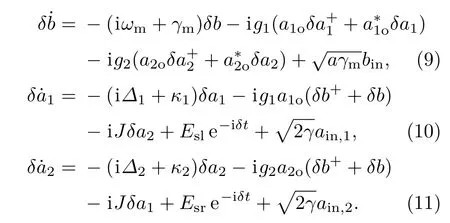
由于量子热噪声项平均值为0,因此可以把噪声项忽略,只保留涨落算符的线性项,通过引入如下变换转到相互作用绘景下∶δb→得到如下线性量子郎之万方程∶

上面方程组中只考虑了算符的平均值.当如下条件满足时∶在红边带条件下∆1≈∆2=ωm,系统在边带可分辨条件下ωm≫κk,机械振子具有较高的品质因子ωm≫ γm,并且振子频率远大于g1|a1o|和g2|a2o|,快速振动项 e±2iωmt可以忽略.m=δ−ωm是信号场与腔肠的有效失谐.为了计算简便,考虑κ1=κ2.

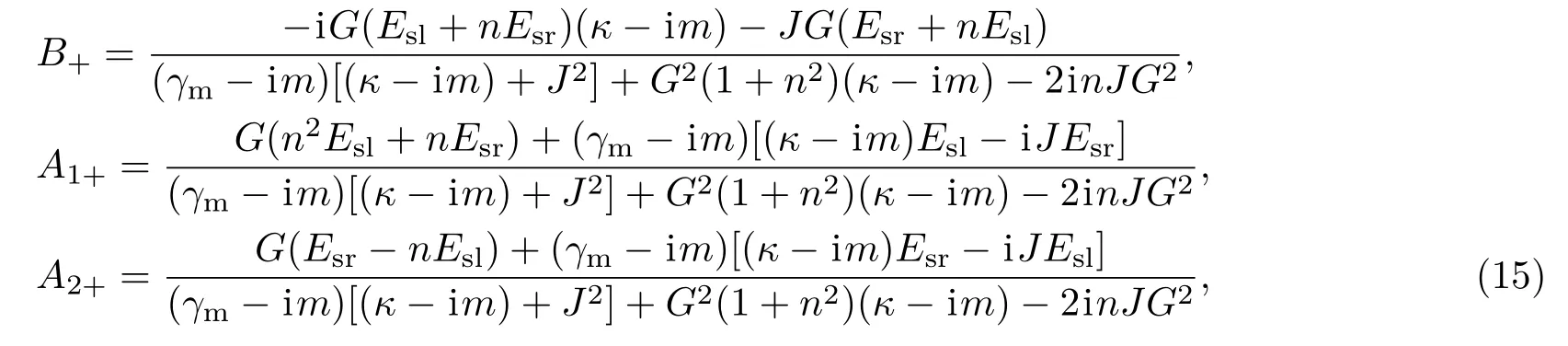
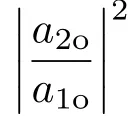
假设不失一般性为a1o和a2o两个实数,由(15)式可以得出两个光腔的输出场Eout_l和Eout_r的表达式.首先根据光腔的输入-输出关系[23]可以得出两腔的输出场与腔模的关系表达式∶

由于两个光腔的输出场Eout_l和Eout_r也满足所以,Eout_l和Eout_r的表达式可以表示为

由于输出场分量Eout_l+与Eout_r+和Esl与探测场Esr有共同的斯托克斯频率ωS,同时,由于光腔机械相互作用是非线性混频过程,因此,输出场分量Eout_l−与Eout_r−具有反斯托克斯相同的频率2ωc−ωS.综合(15)—(17)式可以得到本文重点关注的输出场分量Eout_l和Eout_r∶

3 数值结果与讨论

在讨论中,我们对系统的基本实验参数进行了设定∶激光波长λ=1064 nm,力学振子质量x=145 ng,腔长L=25 mm,腔模弛豫速率κ=2π×215 kHz,力学振子频率ωm=2π×947 kHz.将不同的系统参数区域代入等式(15)和(18),数值结果显示,在我们研究的三模式腔光机械系统中可以分别实现相干完美吸收、相干完美透射以及相干完美合成等有趣的量子相干现象.为了接下来讨论的方便,我们定义几个参数∶N=|Esl|2+|Esr|2/4κ2表示无控制场时的内腔探测光子数;NA1+=|A1+|2/N和NA2+=|A2+|2/N表示腔中归一化后的内腔探测光子数;NB+=|B+|2/N表示归一化的机械激发数;El=|Eout_l+|2/|Esl|2和Er=|Eout_r+|2/|Esr|2表示归一化的输出的探测光子数;ETl=|Eout_l+|2/|Esl|2和ETr=|Eout_r+|2/|Esr|2表示归一化的输出探测场的能量.

3.1 相干完美吸收

首先考虑如何实现相干完美吸收.相干完美吸收表明输入的探测场完全被两个腔模吸收而没有产生任何输出,即是在Esl/0和Esr/0,Eout_l+=0和Eout_r+=0.根据方程(15)得到当条件

同时满足时,相干完美吸收现象才能产生.这个条件与文献[10]中的条件是有点差别的,这是由于在本文的多模式光机械系统中多了一个n因子.不同的有效光机械耦合对输出信号光子数的影响如图2所示.

图2(a)中给出了n=1和J=0时,在不同的有效光机械耦合强度G下,归一化的输出信号光子数El和Er作为有效失谐m/κ的变化曲线,显然相干完美吸收的出现与有效光机械耦合强度有关.结合(18)式可知,当(n2+1)G2＜κ2时,m±为虚数,不会产生相干完美吸收现象;当(n2+1)G2=κ2时,m±=0,此时刚好满足产生相干完美吸收现象的条件;当(n2+1)G2＞κ2时,m±是两个非零的实数,对应两种不同频率的探测场,并且均会产生相干完美吸收现象.因此,相干完美吸收指的是两束输入的信号场被两个腔模和机械模完全吸收而没有反射或透射到腔外,这是由于机械模衰减很快时,向左传播和向右传播的信号场光子数产生了完美的破坏性干涉.

图2(b)给出了在G=1.5κ和J=0时,两腔中的光子数比率n因子对归一化的输出信号场光子数El和Er的影响.随着n因子数的增加,输出信号场表现出明显的模式分裂现象,这是由于增加内腔光子数导致了腔场与机械振子之间的强耦合[2,23].另外,在光机械耦合强度G值固定的情况下,可以通过调节n值的大小,可以非常容易地控制发生相干完美吸收的探测场频率值.

在图2(c)中,我们进一步考虑在G=1κ和n=1时腔与腔之间的耦合强度J对完美相干吸收的影响.发现增加J的数值,输出的信号场光子数并没有被这个三模系统完全吸收,也就是说相干完美吸收现象被两个腔之间的耦合所破坏.因此,对于在三模腔光机械系统中实现相干完美吸收,J参数是一个不好的因子而需要克服掉,尤其是对于两个腔模与一个机械模式相耦合的情况.

由于相干完美吸收是两束输入的信号场被系统完全吸收而没有反射或透射到腔外,研究系统中能量的分布是很有必要的.不同有效耦合对内腔信号场光子数和机械激元的影响如图3所示.

图2 (网刊彩色)不同耦合对输出信号光子数的曲线图 (a)和(b)是J=0时,在不同的有效耦合强度G和腔光子数率n下,输出信号场光子数El(Er)作为输入信号场失谐m/κ的函数;(c)是在G=1.0κ和n=1时,三个不同的腔-腔耦合J所对应的输出信号场光子数El(Er)作为输入信号场失谐m/κ的函数Fig.2.(color online)A graph of the photon number of the output signal with different coupling:(a),(b)The normalized output signal photon number El(Er)as a function of the normalized input signal field detuning m/κ under several different effective opt mechanical coupling rates G and the cavity photon number ratio n at J=0,respectively;(c)the normalized output signal photon number El(Er)for three cavity-cavity coupling strength J under G=1.0κ and n=1.

图3 (网刊彩色)(a)—(c)在n=1和J=0时,在几个不同的有效耦合强度G下,内腔信号光子数NA1+,NA2+激子激元NB+作为m/κ的函数;(d)—(f)腔-腔耦合对NA1+,NA2+,NB+的影响Fig.3.(color online)(a)–(c)The normalized intracavity signal photon number NA1+,NA2+and the normalized mechanical excitation NB+as a function of m/κ for several different values of the effective opt mechanical coupling rate G at n=1 and J=0,respectively;(d)–(f)plot the cavity-cavity coupling strength J that effect NA1+,NA2+and NB+.

图3 (a)—(c)所示为在n=1和J=0时,有效光机械耦合与内腔信号场光子数和机械激元之间的关系.图3(a)和图3(b)表明两个腔的内腔探测光子数相等,而机械激元则是两内腔信号场光子数之和,如图3(c)所示,这是由于机械模与两个腔模相耦合后,机械模接收了来自两个腔模能量的传递.回到单个腔模与一个机械振子耦合的情况,则机械激元与内腔探测光子数相等.图3(d)—(f)给出了腔与腔之间的耦合强度J的情况,当J=0时,输入场能量的传递主要来自于两腔模与机械模的耦合,而当J＞0时,存在腔与腔的耦合,该系统提供了另外一条传递输入场能量的途径,即腔与腔之间的耦合.

需要强调的是,当左右探测场发生相干完美吸收时,左右探测场的能量在腔模媒介的作用下完全被系统中间的机械振子吸收,并快速耗散.因此,发生相干完美吸收时,机械振子的弛豫速率为左右腔模弛豫速率之和,两个腔模和一个机械模式共同分担了输入的能量.

3.2 相干完美透射

在不同的参数机制下,相干完美透射的现象也会在该系统中出现.相干完美透射是输入的信号场会从一个腔传递到另一个腔而不会产生任何能量的损耗.即Esl/0和Esr=0时,ETl=0和ETr=1,也即是在没有右边的信号场时,左边的信号场经过这个三模系统后被完美地透射,并且从右边的腔输出场中能观测到.我们首先考虑实现相干完美透射的条件.根据方程(15)得到当条件

图4(a)和图4(b)在J=0时有效光机械耦合G对两腔的输出信号场能量的影响.当G=0.2κ,相干完美透射出现在m=0的位置,而当G ＞ 0.2κ时,相干完美透射出现在m=0和的位置.相干完美透射是一个纯量子光机械现象,是由于能量从一个腔到另一个腔的传递取决于信号场的无损耗隧穿,这就需要机械振子没有损耗.因此需要机械振子的衰减率γm足够小或者机械振子的品质因子Q足够大.

当增加振子的衰减率或者降低振子的品质因子时,能量从一个腔传递到另一腔的过场中将会产生能量的损耗,而且相干完美透射现象也会突然消失.不同的机制对输出信号场能量的影响如图5所示.

图4 (网刊彩色)在J=0时几个不同有效藕合对输出探测场能量ETl和ETr的影响Fig.4.(color online)The normalized output probe field energy ETland ETras a function m/κ for several G at J=0,respectively.

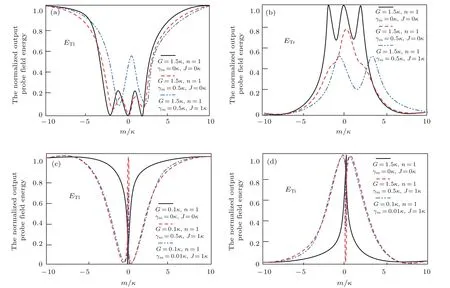
图5 (网刊彩色)在不同的机制下输出信号场能量ETl和ETr的影响Fig.5.(color online)The normalized output signal field energy ETland ETras a function m/κ under different parameter regimes.

图5(a)和图5(b)所示为G=1.5κ和n=1时机械振子的衰减率对相干完美透射的影响,显然相干完美透射过程被破坏.进一步考虑腔与腔之间的耦合J,尽管在γm0时相干完美透射被破坏,依然会在输出信号能量中看到一个类似于相干完美透射的分裂.与γm=0相比,在γm/0时损失的能量被机械模分担.图4显示在J=0时,当G比较小时,相干完美透射只出现在m=0的位置,而当J=1κ时,相干完美透射现象将会转变为类似于光机械诱导透明现象,即使在γm0时,这个现象依然存在,如图5(c)和图5(d)所示.因此腔与腔的耦合度J提供了一个调节相干完美透射与光机械诱导透明之间转变的通道.

需要强调的是,腔与腔之间的耦合度J的变化,对系统的相干完美吸收和相干完美透射的作用是刚好相反的.即J值的增加会减低相干完美吸收,但是提升了相干完美透射现象,反之亦然.也就是说,通过调节腔与腔之间的耦合度J的值,来控制探测场量子的相干强弱,进而控制输出的探测场在“吸收态”和“透明态”之间的转化来实现光开关的功能.

3.3 相干完美合成

最后对系统的相干完美合成量子现象进行研究.当系统的左右两侧的探测场输入的振幅相等的情况下,一侧的探测场出现全反射的同时,另外一侧的探测场出现全透射,这种现象就是相干完美合成量子现象.即Esl=Esr0时,有=0,=2;或=2,=0.根据方程(15)得到相干完美合成的条件∶

其中,

由图6可以看出,当θ=π/2时,在m+=+0.6κ处,=0和=2,但是在m−=−0.6κ处,=2和=0;当θ=3π/2时,在m−=−0.6κ处,=0和=2,但是在m+=+0.6κ处,=2和=0.所以通过改变相位θ从π/2到3π/2的简单调制,我们就可以使探测场从左腔输出变换为从右腔输出,反之,探测场输入也是一样可以通过改变相位变换.也就是说,本文提出的三模光机械系统可以实现一侧的探测场出现全反射的同时另一侧出现全透射的相干完美合成量子现象.

图6 (网刊彩色)输出探测场标准化能量和在不同θ值下随着输入探测场标准化失谐m/κ的变化(a)θ=π/2;(b)θ=3π/2Fig.6.(color online)Output of the probe field normalized energy and in different m/κ values with the input field normalized detuning y curve:(a)θ=π/2;(b)θ=3π/2.

4 结 论

在腔光机械的物理特性的基础上,提出了一种三模光机械系统,在系统左右两侧均有探测场与控制场输入并驱动该系统.我们的分析与数值结果显示,在不同参数机制下,这个三模光机械系统可以出现相干完美吸收、相干完美透射和相干完美合成的有趣量子现象.当相干完美吸收产生时,输入的信号场能量完全转化为内腔场的能量和振子的内部相干振动,满足能量守恒定律.当相干完美透射产生时,由于中间机械振子的弛豫速率非常小,保证从系统一侧输入的探测场在不损失能量的情况下从另外一侧完全透射出来.并且中间力学振子的弛豫速率趋于零,可以保证在一侧的探测场发生完美透射的同时另外一侧的探测场发生全反射,实现相干完美合成.在三模光机械系统中,腔与腔之间的耦合相互作用在该系统中起着重要作用,可以有效操控这些有趣的量子现象.通过设计光学和机械模式器件,该现象可在多模光机械系统中实现.研究和操控相干完美吸收与相干完美透射将在光学开关、光学路由器、光学交换机、光学滤波器等器件上有着潜在的应用.

[1]Aspelmeyer M,Kopparberg T J,Marquardtf2014 Rep.Prog.Phys.86 1391

[2]Grblacher S,Hammerer K,Vanner M R 2009 Nat.Prod.Lett.460 724

[3]Chen X,Liu X W,Zhang K Y,Yuan C H,Zhang W P 2015 Acta Phys.Sin.64 164211(in Chinese)[陈雪, 刘晓威,张可烨,袁春华,张卫平2015物理学报64 164211]

[4]Andrews R W,Peterson R W,Purdy T P,Cicak K,Simmonds R W,Regal C A,Lehnert K W 2014 Nat.Phys.10 321

[5]Teufel J D,Li D,Allman M S 2011 Nat.Prod.Lett.461 204

[6]Verhagen E,Weis S 2012 Nat.Prod.Lett.462 63

[7]Alegre T P M,Chan J 2011 Nat.Prod.Lett.461 69

[8]Fiore V,Kuzyk M C 2011 Phys.Rev.Lett.107 133601

[9]Teufel J D,Donner T,Li D 2011 Nat.Prod.Lett.461 359

[10]Wang Y D,Clerk A A 2013 Phys.Rev.Lett.109 253601

[11]Dobrindt J M,Kippenberg T J 2010 Phys.Rev.Lett.106 033901

[12]Hill J T,Chan J 2012 Nat.Commun.3 1196

[13]Hu Q G,Dong X Y,Wang C F,Wang N,Chen W D 2015 Acta Phys.Sin.64 034209(in Chinese)[朱奇光,董昕宇,王春芳,王宁,陈卫东2015物理学报64 034209]

[14]Ludwig M,Painter O 2012 Phys.Rev.Lett.108 063601

[15]Tian L 2013 Phys.Rev.Lett.109 233602

[16]Dong C,Fiore V,Kuzyk M C 2012 Sci.Prog.334 1609

[17]Qu K,Agarwal G S 2013 Phys.Rev.A 87 031802

[18]Yan X B,Cui C L,Gu K H 2014 Opt.Express 22 4886

[19]Joshi C,Larson J,Jonson M 2012 Phys.Rev.A 86 033805

[20]Wang H,Sha W,Huang Z X,Wu X L,Shen J 2014 Acta Phys.Sin.63 184210(in Chinese)[王辉,沙威,黄志祥,吴先良,沈晶2014物理学报63 184210]

[21]Agarwal G S,Huang S 2014 New J.Phys.16 033023

[22]Liu H,Cao S Y,Meng F,Lin B K,Fang Z J 2015 Acta Phys.Sin.64 094204(in Chinese)[刘欢,曹士英,孟飞,林百科,方占军2015物理学报64 094204]

[23]Lu C P,Yuan C H,Zhang W P 2008 Acta Phys.Sin.57 6976(in Chinese)[鲁翠萍,袁春华,张卫平 2008物理学报57 6976]

PACS∶71.15.Mb,78.20.Ci,42.55.—f,42.55.WdDOI∶10.7498/aps.66.107101

*Project supported by the National Natural Science Foundation of China(Grant No.61363047),the Science and Technology Innovation Project of Jiangxi,China(Grant No.2014GJJ12255),and the Science and Technology Innovation Project of Foshan,China(Grant No.2016AG100382).

†Corresponding author.E-mail:gov211@163.com

Coherent perfect absorption and transmission of a generalized three-mode cavity optico-mechanical system∗

Zhang Yong-Tang†
(Department of Computer Science and Technology,Guangdong Neusoft Institute,Foshan 528225,China)

14 December 2016;revised manuscript

1 March 2017)

With the rapid development of nano-physics and quantum optics,optico-mechanical coupling system is developing toward the miniaturization and lightweight.The physical characteristics of optical cavity and applications of opticmechanical devices have received much attention.In this paper,a generalized three-mode cavity optico-mechanical system is presented,the steady-state responses of the system to the characteristics of weak detection of light absorption and dispersion in several different coherent driving modes are studied.Situated in the middle of system is a portable total reflection mechanicaloscillator with a reflectance of 100%,and located on each side is afixed optical cavity mirror with partial transmittance,Three-mode cavity optical mechanical system consists of“fixed-mirror,removable-vibrator,fixed-mirror”structure.in which the two optical cavities are coupled by coupling a stronger control field and weak probe light with the same mechanicaloscillator.Analysis and numerical results show that under the mechanism with different parameters,due to nonlinear effect of pressure,in the three-mode cavity optical mechanical system,there appear some interesting quantum coherent phenomena such as coherent perfect absorption,coherent perfect transmission and coherent perfect synthesis.When coherent perfect absorption occurs,the mutual conversion between input signal power full- field energies and oscillator vibration of internal coherence can be realized,and the law of conservation of energy is satisfied.When relaxation rate due to mechanicaloscillator is very small,the coherent perfect transmission is completely transmitted from the system side of the input field to the other side in the case of no loss of energy.And mechanical relaxation rate of the oscillator approaches to zero in the middle,which can ensure that the perfect transmission of the detection field takes place on one side,and the field total reflection and coherent perfect synthesis happen on the other side of.In addition,we alsofind that the adjustment of coupling between cavity and cavity can change the intensity of the probe field of quantum coherent control thereby realizing that the output of the detection field is transformed between coherent perfect absorption and coherence transmission;through simple phase modulation the output direction and input direction of detection field for left cavity-right cavity can swap mutually.So,these dynamic controls in quantum information networks can be used to construct some optical devices with special functions,such as photon switch,photo router,photon exchange machine,etc.

∶physical characteristics,optical-mechanical coupling system,quantum optics,optical communication

∗国家自然科学基金(批准号:61363047)、江西省自然科学基金(批准号:2014GJJ12255)和佛山市科技创新项目(批准号:2016AG100382)资助的课题.

†通信作者.E-mail:gov211@163.com

©2017中国物理学会Chinese Physical Society