例说轴对称在解题中的妙用

重庆市鲁能巴蜀中学校 杜星兰

例说轴对称在解题中的妙用

重庆市鲁能巴蜀中学校 杜星兰

本文研究的主要目标就是应用轴对称理论尝试解题，并从中发现轴对称解题存在的实践意义，让学生更好地掌握科学的解题方法，并沿用到生活当中。

轴对称；解题；妙用

伴随时代的不断发展以及社会文明的不断进步，人们越来越重视教育工作的质量升级目标，通过科学的学习方式能够培养学生更加优秀的综合能力。因此，本文就针对轴对称的解题思路进行分析，希望能够让学生掌握更为灵活的解题思维。

一、选择最优路线问题

采取轴对称的方式在解题的过程中充分应用，能够满足实际的解题需求，即应用翻折变换的方式勾画基础途径，进而获得解题思路，从而得到答案。本次研究首先从选择最优路线的解题用法入手，从中体会解题应用轴对称的妙处。

例1 如图1所示，瓜农从A处去挑水，然后回到B处，A处为瓜农的家，B处是瓜棚的位置，尝试寻找在什么位置取水能够走最短的路程？解题：寻找A点关于直线CD的翻折变换对称点A1，选择连接A1B与直线CD交于点M。根据题目给出的信息进行解题，理顺对称轴的性质能够得知，AM=A1M。因为AM+BM=A1M+BM=A1B，因此获得两点之间的直线最短。所以，点M为本题答案。

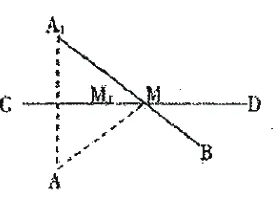
图1

例2 根据图2理解，两条道路之间形成的夹角α＜90°。在两条道路之间存在一个汽油储存地点，该地点表示为P。如果希望在两条道路上都设置一个加油站，应当能选择的位置是哪里？要求能够将两个加油站设置在与汽油储存地点分别达到比较近的位置，即从汽油储存位置到一个加油站，再到另一个加油站后回到原点的距离最近。尝试分析这样的题目，就是把生活中实际存在的问题转化为数学理论。即已知条件为∠ABC和∠ABC内的P点，∠ABC为α，且α＜90°，在射线BA和BC的线路中寻找符合要求的Q点、R点，促使折线(PQ+QR+RP)后得到的线路长度最短。这样的方式说明，如果解题过程中应用轴对称中的翻折变换方式，就能够从P点找到BA和BC的轴对称点，即P1，P2，然后就能够为找寻最短路径的问题找到解题方案。具体解题方案就是，在BA和BC两侧找到关于P点的对称点，分别是P1，P2，并连接P1，P2，与BA、BC交于点Q和点R，最终获得的点Q、点R就是答案。

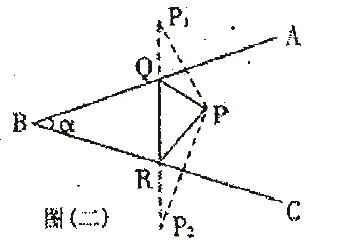
图2

二、台球运动反射原理

台球运动在固定的桌面范畴内，存在不同的球位置，因此能够促成非常有趣的数学题目，应用轴对称的翻转变换方式进行解题，可以获得很多科学的思路，进而满足数学教学的实际需求。如图3所示，在矩形的台球桌中存在C，D，E，F四个点，其中A、B分别表示黑色球和白色球，假使通过球杆击打黑色球，就能够在黑色球达到桌边时碰撞EF线，然后反弹回去恰好击中白色球，希望达成这样的击打线路，应当如何控制黑色球的运动轨迹路线？为了能够解答这道题目，第一步需要在台球桌的线路内寻找能够反弹球的线路及其规律，将A球击打到台球桌面的EF射线上，就会遇到M点，进而通过反弹可以满足集中B球的要求，MN就是EF的垂线，∠AMN和∠BMN分别称之为入射角和反射角。了解并掌握自然反射中存在的规律信息，就能够发现，假如光线从A的角度射入，然后通过镜面的操作呈现出M反射就会到达B点。∠AMN与∠BMN是相等的，这也是反射原理的内容，而出现在M点的角度也是最佳的反射点，首先，通过延长BM获得A1，进而能够得到MA1=MA，并且可以发现A在EF右侧存在对称点，即A1，连接A,B与EF交于M点，即M是最优点。其次，在EF上存在的任意一个点再到A、B点上的距离之和，都显示AM+MB为最短线路。

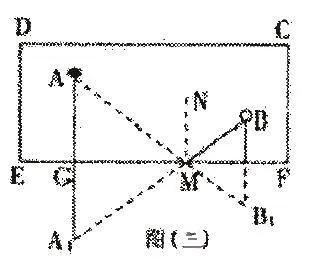
图3

三、几何证明题中的应用

利用轴对称和翻转变换的理论能够在几何证明题中充分应用，并辅助得到良好的题目解答方案。在几何图形中，非常常见的图形都是由线、角组成的，其中包含等腰三角形等。为了能够证明几何题目中才能存在的对称关系，就需要根据翻折变换的方式将不对称的图形转变为轴对称图形，进而达成解题证明的需求。如图4所示，△ABC是等边三角形，将线段BA延长到E，再将线段BC延长到D，使AE与BD相等，然后连接CE和DE，求证CE=DE。尝试分析，假如CE=DE，那么在CD的中垂线两侧存在对称的线段关系，根据这一原则进行图形的补充，采取翻折变换的方式能够补全图形，最终延长BD到 F，其中DF=BC，补充一个轴对称的图形，就能够获得等边三角形EBF，通过证明△EBC≌△EFD即可获得证明结果。

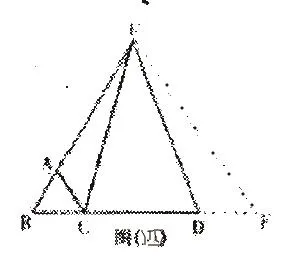
图4

通过切实有效的分析、探讨和总结能够发现，在数学教学过程当中，应当重视对学生感性认知的调节，满足学生自身对实践学习的要求，让学生在解题的过程中，通过自己的操作实现对轴对称理论的理解，进而能够让学生在翻转变换的过程中体验相关的信息，进而借助自身学习到的理论实现对生活中存在问题的解答，从而让学生在大脑思维中构建数学思维模式，让学生更好地将学习到的数学知识应用到生活当中。

[1]李志英.初中生关于轴对称知识理解的研究[D].河北师范大学，2014.

[2]陈丞.对初二学生解决轴对称图形问题的研究[D].苏州大学，2014.

[3]王连东.轴对称塑性变形问题的广义滑移线方程推导[J].燕山大学学报，2000（03）：250-253.