函数概念相关母题设计研究——定义域、解析式、值域

江苏省昆山市费俊龙中学 徐玉明

函数概念相关母题设计研究
——定义域、解析式、值域

江苏省昆山市费俊龙中学 徐玉明

函数已经成为高考考查的重点内容，通过研习历年高考试卷发现，函数相关试题基本可以归纳为定义域、值域以及解析式三大考点。如若在解题过程中，不能够透过现象看本质，较易出现纰漏，进而与正确的答案失之交臂。函数定义并不复杂，但要理解清晰也确实存在一些难度，作为高考考查的重点内容，函数概念对应的相关考点还是存在一些难度的。笔者为了解决函数这一个重难点，从定义域、解析式、值域这三大考点出发，分别设计了函数母题，既能够锻炼和提高学生的解题能力，促使学生掌握技巧，还能够锻炼学生的数学逻辑。

一、求函数f（x）的定义域

从函数概念中可以看出，函数及其定义域存在密切的关系，是不可分割的，简单来讲就是每个函数都有其对应的定义域。因此，要想求得函数的解析式，不仅要求出变量间的对应法则，还要求出函数的定义域。通过分析历年高考试卷发现，求函数定义域一般可以分为两大类，具体为：

1.知函数解析式，求函数定义域

母型和方法：该类型题目在解决的过程中，必须要清晰函数解析式有意义需要满足的条件，同时还要能够意识到函数的定义域就是要满足函数的解析式具有意义。函数解析式要具有意义，就必须要满足七个方面：一是分式的分母不能够为零；二是开偶次方根的被开方数不能够为负数；三是对数函数的真数必须要为正数；四是指数、对数函数的底数必须大于0且不等于1；五是0的0次幂不具有意义；六是三角函数中的正切函数且 k∈Z），余切函数y=cotx（x∈R，x≠kπ，k∈Z）；七是实际问题中变量（x）要具有实际意义等。

2.知一函数解析式，求另一函数定义域

例2 已知函数f（x）的定义域为[1，3]，那么函数f（2x-1）的定义域为 。

分析：根据函数概念可以知道，函数的定义域就是指函数自变量x的取值范围。根据已知条件和函数的对应法则可以了解到：f（x）的定义域为[1，3]→1≤2x-1≤3，通过计算求得函数f（2x-1）的定义域为[1，2]。

母型与方法：已知简单函数f（x）的定义域为[a，b]，求复合函数f[g（x）]的定义域。该类题目需要满足的条件就是函数g（x）的自变量x在函数f（x）的定义域的取值范围，就是复合函数f[g（x）]的定义域。

二、求函数f（x）的解析式

根据已知条件求取函数f（x）的解析式，是当今高考中的考点之一，因此必须要引起足够的重视。求函数f（x）的解析式可以归纳为三大类，具体为：

1.已知函数类型且知函数图像上的三个点

例3 已知函数f（x）的图像为抛物线，且点（2，0）、（-2，0）、（4，0）在函数f（x）的图像上，求函数f（x）的解析式。

母型与方法：通过已知条件，明确函数的特征，求取函数的解析式，一般会通过“待定系数法”求取。函数特征不同，图像不同，要能够根据图像联想到函数的特征，设定出函数的一般式，将相关参数代入即可。

2.已知复合函数解析式，求简单函数解析式

例4 已知函数f（x-3）=x，求函数f（x）的解析式。

分析：该类题目解决的过程中，往往会运用换元法。设x-3=g，则x=g+3，故f（g）=x+3，即f（x）=x+3。

母型与方法：已知复合函数f[g（x）]的表达式，求简单函数f（x）的解析式时，一般会选用换元法，偶尔也会运用到配凑法。这里就概述一下换元法。换元法的母题：令g（x）=t，求出x=h（t），之后代入就可以获得函数f（x）的解析式。

3.已知函数f（x）满足等式，且其为等式中的未知量

分析：分析题目发现只有一个已知条件，根本不足以解决问题。因此，必须要根据已知条件去构造其他条件。

母型与方法：如若已知函数f（x）满足一个等式，且f（x）是该不等式中的未知量，且明确与其他未知量之间的关系，如f（x）、此时，就可以根据已知不等式，通过代换，构造另一个等式，从而得到一个方程组，就能够获得函数f（x）的解析式。

三、求函数f（x）的值域

值域是函数的三大元素之一，更是考试考查的重点内容。从函数特征来讲，函数的种类具有多样性的特点，导致求函数值域的试题数不胜数。笔者通过研究分析，从方法来讲，求函数值域的方法有限，大致可以归纳为八种，分别为：直接法、配方法、换元法、反函数法、不等式法、判别式法、单调性法以及数形结合法。这里，就以“数形结合法”为例进行阐述。

分析：该类型题目看起来非常复杂，潜意识就会觉得难度大。从几何意义上来讲，根号可以看作是点到点的距离，在此基础上，可知：f（x）表示点P（x，0）到点A（0，2）、点B（-1，-3）两点之间的距离和，且点P位于x轴上任意一点。这样一来，题目就转化成为直线上任意一点到两个顶点的距离的取值范围。根据转化题意，可以作出图形，如图1。

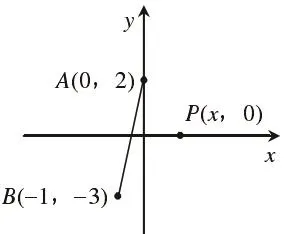
图1 函数f（x）转化后的图形

母型与方法：面对具有明显几何特征的函数时，可以采用“数形结合法”求取函数的值域。该方法具有直观、易懂的特点。

上述皆为与函数概念相关的函数母题，这里讲述到的母题并不全面，而是一些高考中常常遇到且学生理解难度较大的。函数母题与函数学习有非常密切的关系，因此在日常的教学中，要认识到函数母题的重要性，加深学生对于母题的认识、理解，最好能够实现灵活运用，从而取得良好的学习效果。

[1]钟志敏，李士锜.高一学生函数对应关系的理解的研究[J].数学教育学报，2010（01）.

[2]卫德彬.函数概念难学的原因及教学对策[J].中学数学教学，2009（03）.