致密砂岩双重介质复合油藏偏心井试井分析

姬安召，王玉风，徐有杰，陈占军，刘雪芬

（1.陇东学院能源工程学院，甘肃庆阳 745000；2.西南石油大学油气藏地质与开发国家重点实验室，四川成都 610500）

致密砂岩双重介质复合油藏偏心井试井分析

姬安召1，王玉风1，徐有杰2，陈占军1，刘雪芬1

（1.陇东学院能源工程学院，甘肃庆阳 745000；2.西南石油大学油气藏地质与开发国家重点实验室，四川成都 610500）

针对天然裂缝性致密砂岩油藏，研究了3种外边界条件（无穷大、定压、封闭）及内边界定产量生产问题，并建立了考虑应力敏感性和交界面阻力的不稳定渗流试井分析模型。先对此模型作参数无量纲化处理；然后通过零阶摄动法以及利用Laplace变换，求得线性化后的无因次储层压力的Laplace空间精确解；最后采用Stehfest数值反演方法，绘制了3种不同边界致密砂岩双重介质复合油藏偏心井压力和压力导数的典型图版。通过图版分析可知：渗流过程划分为9个阶段；随着偏心距不断增大，径向流阶段持续的时间越长；一区和二区的交界面阻力越大，“驼峰”越高；应力敏感系数越大，相对于一区来说二区压力和压力导数曲线上翘更明显。

偏心井；复合油藏；应力敏感；交界面阻力；零阶摄动

试井分析作为油气藏动态监测和地层参数求取的重要手段，国内很多学者对试井解释模型作了一定程度的研究，并绘制了一定的样板曲线。1965年Warren等[1]对天然裂缝储层的压力动态进行了分析，求解出了双重介质油藏的解析解。1989年Turki等[2]建立了复合油藏试井解释模型并且进行了压力曲线分析。1994年刘义坤等[3]建立了均质复合油藏试井解释模型并给出了解析解。1995年贺胜宁等[4]建立了双重介质复合井解释模型并做出了典型曲线。2005年刘启国等[5]建立了考虑交界面阻力影响的双重介质复合油藏试井解释模型并做出了典型曲线。2013年李林凯等[6]建立了低渗透双重介质试井解释模型并进行了数值求解。2016年姜瑞忠等[7，8]建立了偏心井双重介质复合油藏试井解释模型并绘制了典型曲线，但并未考虑应力敏感及交界面阻力对试井结果的影响。在前人研究成果的基础之上，本文建立了致密砂岩地层存在天然裂缝的双重介质双区径向复合试井解释模型，考虑交界面阻力和应力敏感的影响，采用零阶摄动解和拉氏变换，求解出不同类型边界地层的拉氏空间的解，并对不同参数进行分析，做出了典型试井图版，为考虑交界面阻力的致密砂岩双重介质径向复合偏心井油藏的试井提供了理论依据。

1 模型建立与求解

1.1 物理模型

对于致密砂岩油藏来说，在不断的开采过程中，地层压力不断的下降，地层渗透率不断的发生变化，根据文献[9]，应力敏感可由（1）式表示。

对于致密砂岩复合油藏的偏心井来说，假定a为一采油井，b为一观测井，a井与b井之间的距离为r，a井与b井到地层中心的距离分别为ra、rb，ra与rb之间的夹角为θ，一区与二区之间的流体通过裂缝连通，裂缝与裂缝之间存在交界面阻力，其示意图（见图1）[7，8]。

为了更好地建立致密砂岩双重介质复合油藏偏心井试井数学模型，模型的基本假设为[10]：各区内流体为单相可压缩的流体，忽略重力和毛管力的影响；考虑井筒储存效应和表皮效应的影响；各区流体均符合达西平面径向渗流规律，等温渗流；流体驱替方式为活塞驱替；油层均质等厚；考虑接触面阻力的影响；两区间的流体流动发生在裂缝之间。

1.2 试井数学模型

在极坐标系中，根据质量守恒关系，考虑应力敏感（1）式关系，建立双重介质双区径向复合油藏偏心井的渗流微分方程，一区裂缝渗流微分方程为[10，11]：

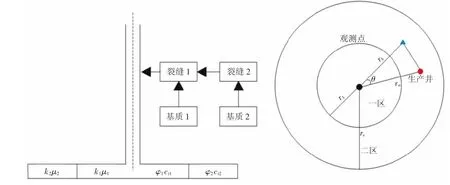
图1 偏心井复合油藏物理模型示意图Fig.1 Sketch of physical model of off-center well composite reservoirs

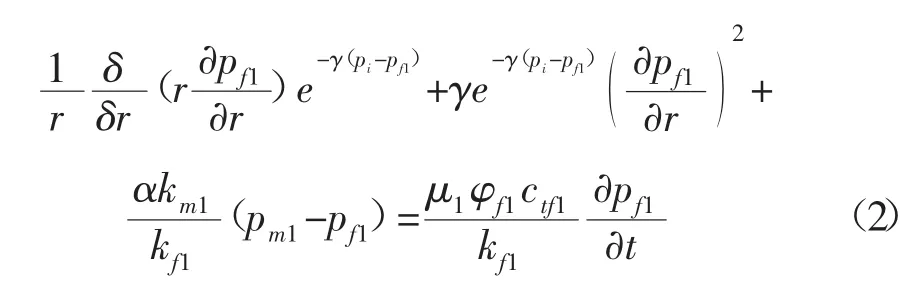
一区基质渗流微分方程为：

式中：pi-原始地层压力，0.1 MPa；pf1、pf2-一区、二区的裂缝系统的流体压力，0.1 MPa；pm1、pm2-一区、二区的基质系统的流体压力，0.1 MPa；kf1、kf2-一区、二区的裂缝系统的渗透率，μm2；km1、km2-一区、二区的基质系统的渗透率，μm2；γ-应力敏感系数，小数；μ1、μ2-一区、二区的流体的黏度，mPa·s；φm1、φm2-一区、二区的基质的孔隙度，小数；φf1、φf2-一区、二区的裂缝的孔隙度，小数；ctm1、ctm2-一区、二区的基质的综合压缩系数，（0.1 MPa）-1；ctf1、ctf2-一区、二区的裂缝的压缩系数，（0.1 MPa）-1；t-生产时间，s；α-形状因子。

内边界井筒储集效应条件：

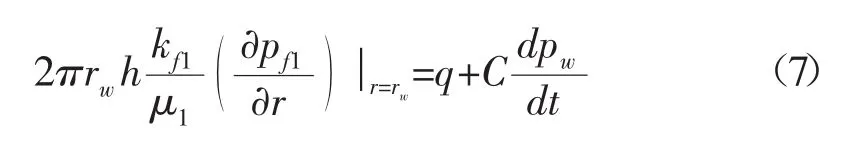
式中：q-单井的产量，cm3/s；C-井储系数，cm3/（0.1 MPa）；rw-井筒半径，cm。

内边界表皮效应：

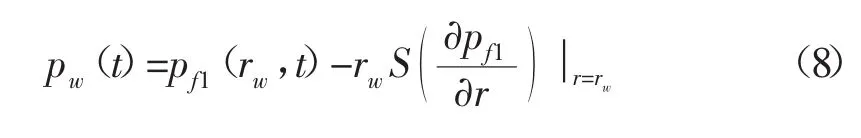
式中：S-表皮系数，小数；pw-考虑井底污染后压力，0.1 MPa。

初始条件：

当交界面流体速度相等时：

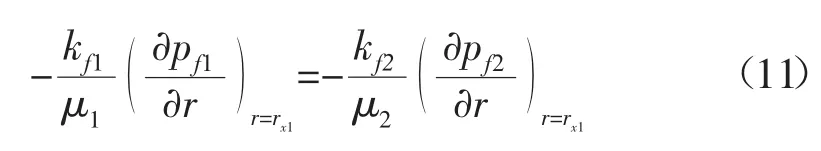
外边界条件，对于无限大地层：

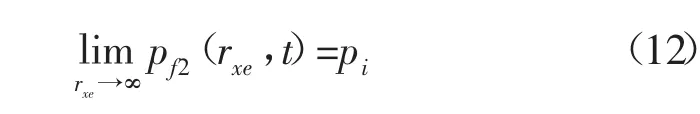
圆形封闭地层：

圆形定压地层：

为了便于求解上述微分方程，定义如下无量纲参数。

内外区无量纲压力：

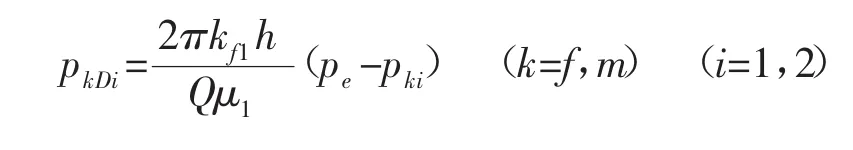
1.3 试井数学模型求解

上述微分方程（2）（4）式均含有与应力敏感系数相关的非线性项，为了解决此问题，需要引入如下变换关系式[12，13]：

对于（15）式只考虑零阶摄动解，将上述方程（2）-（14）进行首先采用上述定义的无量纲参数进行无因次化，然后经过（15）式的变换，最后再对tD进行拉普拉斯变换[14]，可得到拉氏空间考虑交界面阻力双重介质复合油藏偏心井的模型：

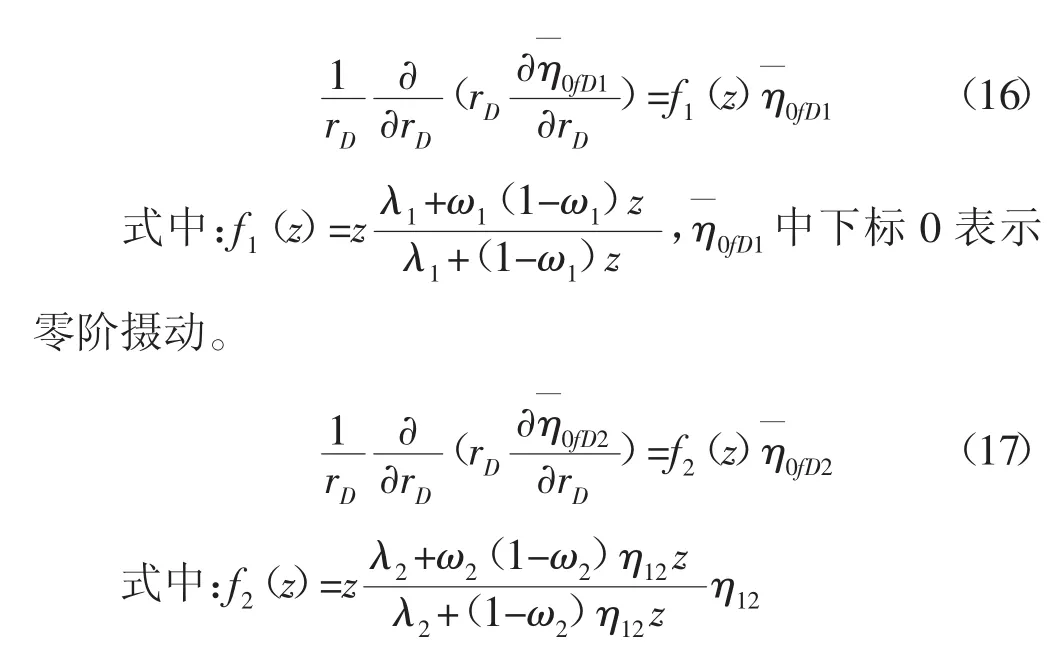
通过上述变换，考虑井储效应边界条件无量纲化拉普拉斯变换后的结果为[15]：

考虑交界面阻力的压力相等无量纲化拉普拉斯变换：

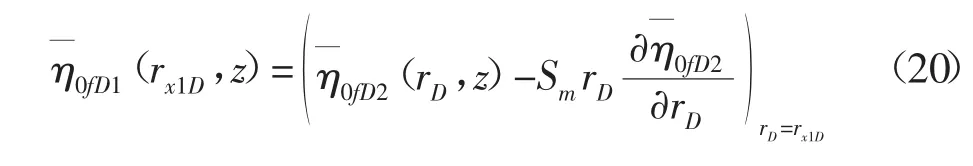
考虑速度相等无量纲化拉普拉斯变换：

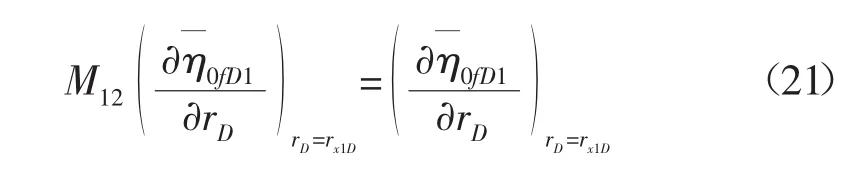
无限大地层边界无量纲拉普拉斯变换：

圆形封闭地层边界无量纲化拉普拉斯变换：

圆形定压地层边界无量纲化拉普拉斯变换：

方程（16）和（17）式的通解分别为：

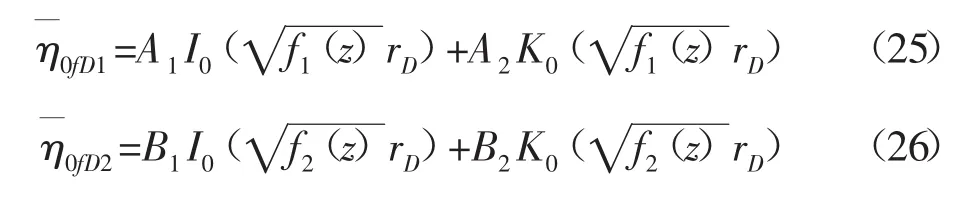
为了求解方程（25）（26）式的系数 A1、A2、B1和 B2，将内边界定产条件，井储系数条件，外边界条件，交界面压力相等条件与速度相等条件代入（25）（26）式。根据Bessel函数I0的性质，可知系数B1在无限大地层中为0，在定压与封闭边界中，系数B1可由B2表示。因此可得关于的方程组。将以上方程组写成矩阵形式为：

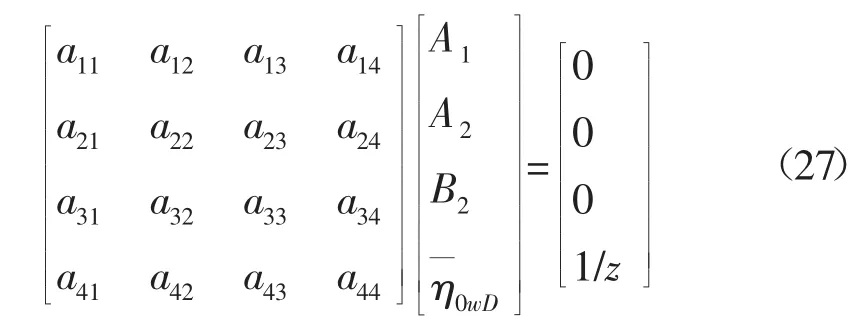
对于上述方程组（27）式进行整理，可以得到不同边界情况下的系数。

无限大地层边界情况下的系数：

外边界封闭地层情况下的系数：

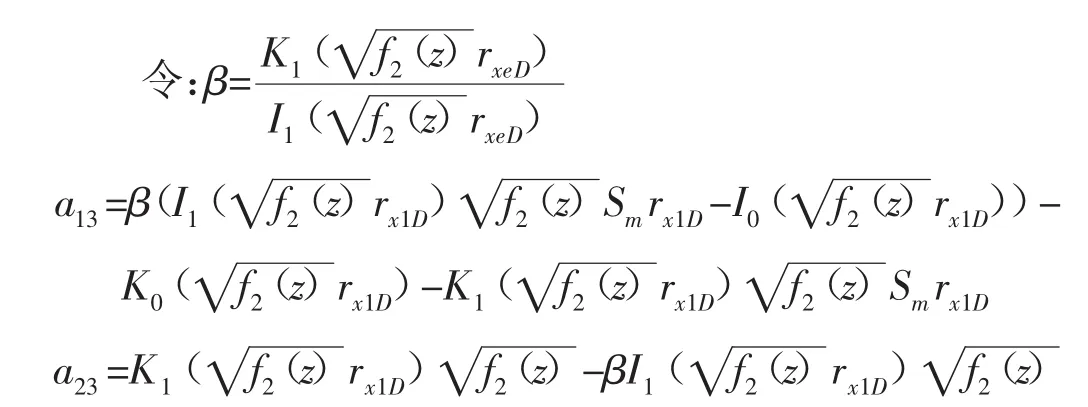
其余系数与无限大地层情况相同。

外边界定压地层情况下的系数：

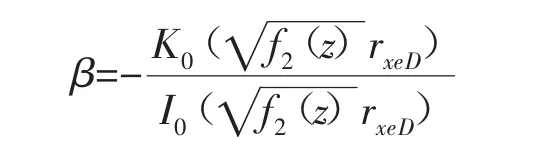
其余系数与外边界封闭地层情况相同。

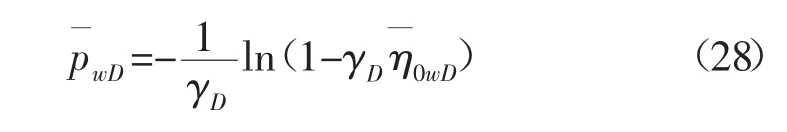
2 特征曲线分析

利用Stehfest数值反演方法[16，17]通过MATLAB编程对（28）式进行数值反演，可得到三种不同外边界条件下无因次压力和压力导数与无因次时间的关系曲线。致密砂岩偏心井试井解释理论图版（见图2），致密砂岩双重介质双区复合油藏偏心井试井解释理论曲线可以划分为九个流动阶段，第①阶段为井筒储集效应阶段，其压力和压力导数为一条45度斜线；第②阶段为井筒到径向流的过渡阶段，其压力导数曲线表现为“驼峰”的形状；第③阶段为一区裂缝径向流阶段，其压力导数曲线表现为一条水平线；第④阶段为地层内基质的流体向裂缝窜流的一个过程，在压力导数曲线上主要表现为一个很明显的“凹子”；第⑤阶段为基质内流体的径向流阶段，在压力导数曲线上主要表现为一条水平线；第⑥阶段为一区到二区的过渡流阶段，考虑交界面阻力时过渡段呈现出一个明显的“驼峰”；第⑦阶段为二区裂缝径向流阶段，其压力导数曲线上表现为一条水平线；第⑧阶段为二区基质内流体向裂缝过渡的阶段，在压力导数曲线上也表现为一条水平线；第⑨阶段为二区基质流体径向流阶段，压力导数曲线为一条水平线。

应力敏感指数对压力和压力导数影响曲线图（见图3），对于双区双重介质复合油藏来说，压力敏感指数对一区和二区的压力导数曲线都有影响，主要表现为径向流阶段压力导数曲线上翘，相对于一区来说，应力敏感指数对二区的影响更大，主要是因为压力波迅速通过一区，储层岩石发生本构变形慢，而压力波传递到一区外边界时，一部分压力波已经消耗，压力波传播的缓慢，储层岩石随着压力传播的同时发生本构变形，所以二区压力导数曲线上翘更明显。

交界面阻力影响曲线图（见图4），交界面阻力主要影响一区和二区的过渡流阶段压力导数曲线形态，当不考虑交界面阻力时，压力导数为一平缓过渡曲线。当考虑交界面阻力时，一区到二区的压力导数曲线呈现出一个“驼峰”形。由于应力敏感指数的影响，在二区压力导数并不重合。

偏心距对曲线的影响（见图5），偏心距越大，二区径向流阶段压力导数水平段越长，压力波通过一区所需要的时间越长，反之亦然。

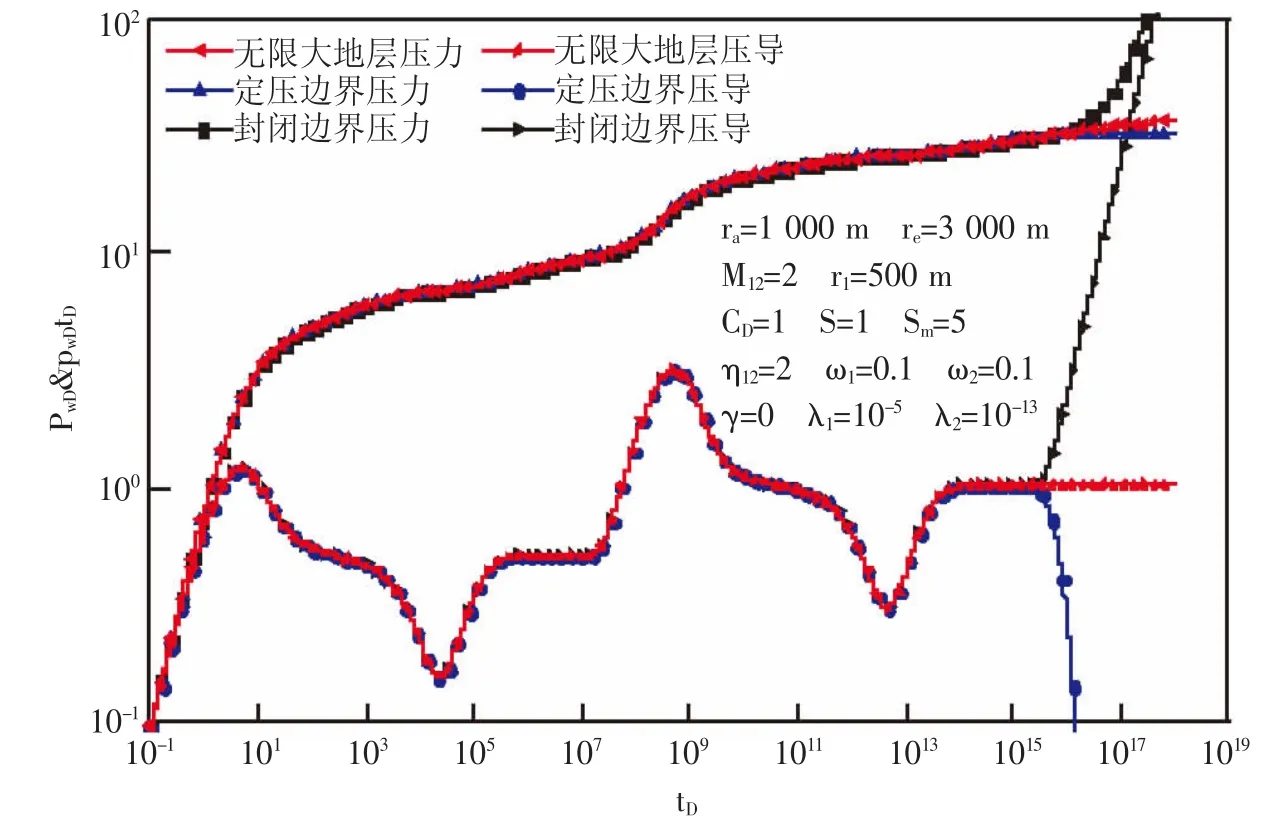
图2 致密砂岩双重介质双区复合油藏偏心井理论曲线Fig.2 Theoretical curve of off-center well of double-zone composite with tight sandstone double medium reservoir

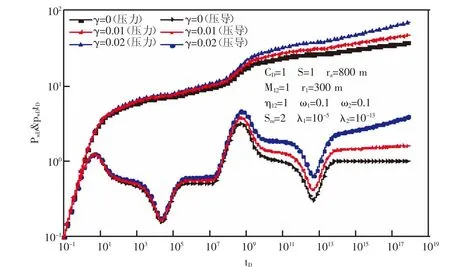
图3 应力敏感指数对压力与压力导数的影响Fig.3 Effect of stress sensitivity index on the pressure and pressure derivative

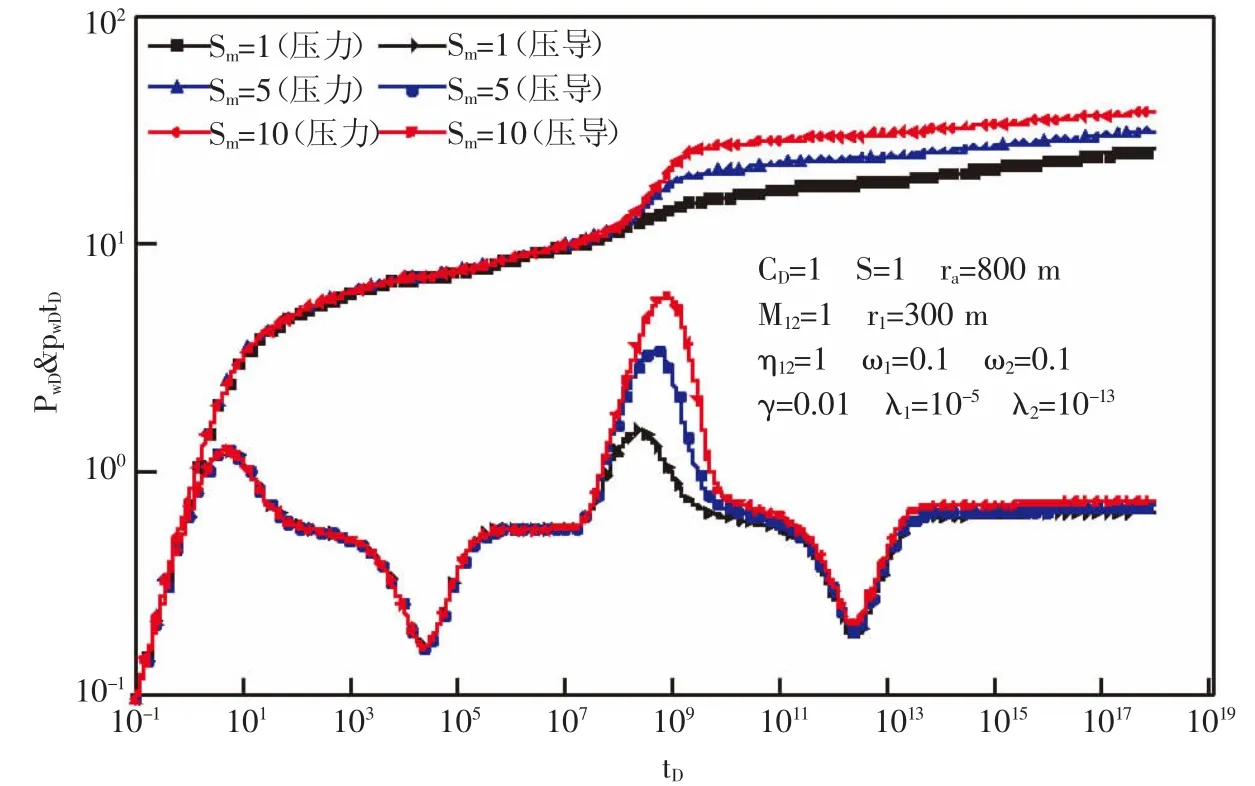
图4交界面阻力对压力与压力导数的影响Fig.4 Effect of interface resistance on the pressure and pressure derivative

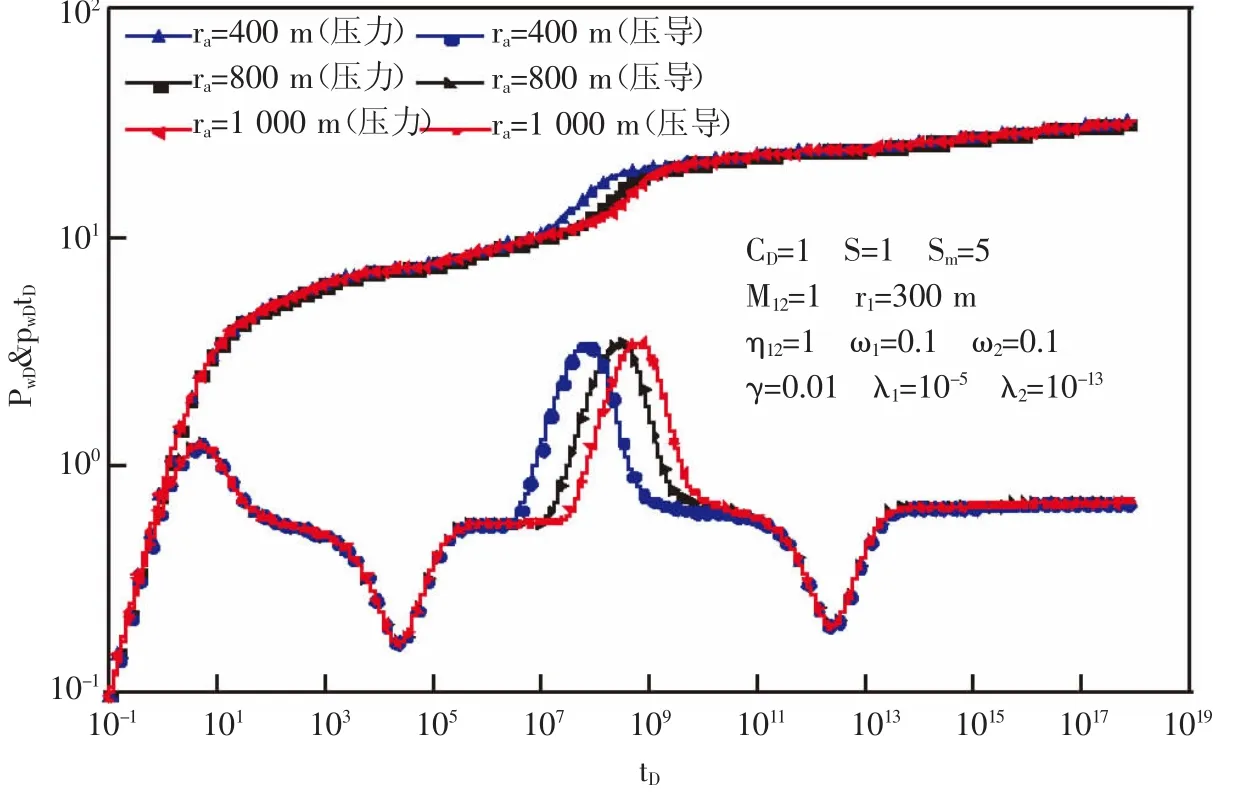
图5 偏心距对压力与压力导数的影响Fig.5 Effect of off-center distance on the pressure and pressure derivative

流度比对复合曲线的影响（见图6），流度比反映了两区流体流动能力的比值，流度比小于1，说明一区流体流动性能差，所以在二区压力导数曲线低于一区，反之亦然；流度比等于1，说明两区流体流度能力相当，只是由于应力敏感的影响，二区压力导数曲线上翘更明显。

3 结论

（1）通过建立考虑交界面阻力和应力敏感影响的双重介质复合试井解释模型，求出拉普拉斯空间的解析解，再通过Stehfest方法进行数值反演，绘制出实空间的压力与压力导数典型曲线。典型曲线一共划分为9个流动阶段，整体上压力导数曲线呈现出先平缓后上升后平缓的特征，而且凹凸不平。

（2）应力敏感影响整个流动阶段，但是对二区的影响更大，随着应力敏感指数不断增大，在后期压力和压力导数曲线表现为“上翘”。

（3）内区半径越大，一区径向流动的时间越长，表现为一区径向流阶段压力导数曲线越长。

（4）一区二区流度比越大，二区径向流阶段，压力导数上所表现出的是水平段越高，反之亦然。

［1］ Warren J E，Root P J.Behavior of naturally fractured reservoirs［J］.Society of Petroleum Engineers Journal，1963，3（3）：245-255.

［2］ Issaka M B，Ambastha A K.Decline curve analysis for composite reservoirs［J］.Journal of Canadian Petroleum Technology，1998，37（6）：17-24.

［3］ 刘义坤，等.均质复合油藏试井分析方法［J］.石油学报，1994，15（1）：92-100.

［4］ 贺胜宁，冯异勇，贾永禄.双重介质复合油气藏试井分析模型及压力动态特征［J］.天然气工业，1995，15（5）：53-56.

［5］ 刘启国，冯宇，董凤玲.受界面附加阻力影响的双重介质径向复合油藏试井解释模型研究［J］.油气井测试，2005，14（3）：11-14.

［6］ 李林凯，姜瑞忠.低渗透油藏双重介质试井［J］.辽宁工程技术大学学报（自然科学版），2013，32（3）：353-356.

［7］ 姜瑞忠，郜益华，孙召勃，等.双重介质复合油藏偏心井试井分析［J］.新疆石油地质，2016，37（3）：327-331.

［8］ 姜瑞忠，郜益华，孙召勃，等.基于点源解的偏心井试井典型曲线分析［J］.东北石油大学学报，2016，40（4）：80-89.

［9］ 王建忠，姚军，张凯，等.变渗透率模量与双重孔隙介质的压力敏感性［J］.中国石油大学学报（自然科学版），2010，34（3）：80-88.

［10］ 卓红，何秀玲，王新海，等.低渗压敏双重孔隙介质油藏试井分析［J］.油气井测试，2013，22（3）：17-22.

［11］ 万义钊，等.缝洞型油藏三维离散缝洞数值试井模型［J］.力学学报，2015，47（6）：1000-1009.

［12］ 何毅.几类含奇异摄动的椭圆型方程解的存在性、集中性与多解性的研究［D］.武汉：华中师范大学，2015.

［13］ 孙美玲.奇异摄动问题的多尺度高效数值模拟研究［D］.扬州：扬州大学，2015.

［14］ Zakian V.Numerical inversion of laplace transform ［J］.Electronics Letters，1969，5（6）：120-121.

［15］ Vongvuthipornchai S.Well test analysis of data dominated by storage and skin ［J］.Spe Formation Evaluation，1987，2（4）：618-628.

［16］ Benedict Dingfelder，Weideman J A C.An improved talbot method for numerical laplace transforms inversion［J］.Numerical Algorithms，2015，68（1）：167-183.

［17］ 卢德唐.现代试井理论及应用［M］.北京：石油工业出版社，2009.

Off-center well test analysis for composite dual-porosity tight sandstone oil reservoirs

JI Anzhao1，WANG Yufeng1，XU Youjie2，CHEN Zhanjun1，LIU Xuefen1
（1.Energy Engineering Institute，Longdong University，Qingyang Gansu 745000，China；2.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation，Southwest Petroleum University，Chengdu Sichuan 610500，China）

For natural fractured tight sandstone oil reservoirs,the problem about fixed output was addressed in 3 outer boundary conditions（infinite boundary,constant pressure and closed boundary）and inner boundary conditions,to build a well test analysis model for unsteady seepage flow in view of stress sensitivity and interface resistance.Firstly,the model of dimensionless parameter was processed,the zero-order perturbation method and the Laplace transform were used to get the exact solution of dimensionless reservoir pressure in the Laplace space with the linearized model.Finally,the method of Stehfest numerical inversion was used,and a typical chart of pressure and pressure derivatives under three different boundary conditions were drawn off-center well of composite dual-porosity tight sandstone oil reservoirs.From the analysis of the plate,it was concluded that,the seepage process was di－vided into nine stages.With the increase of the eccentricity,the longer that the radial flow continues.The bigger the interface resistance between NO.1 and NO.2 blocks,the bigger the stress sensitive coefficients are.Compared to the NO.1 block,NO.2 block's pressure curve and pressure derivative curve upturned more obvious.

off-center well；composite oil reservoirs；stress sensitive；interface resistance；zero-order perturbation

TE344

A

1673-5285（2017）07-0019-07

10.3969/j.issn.1673-5285.2017.07.005

2017－06-05

甘肃省自然科学基金，项目编号：1606RJZM092；甘肃省青年科技基金，项目编号：1606RJYM259，1506RJYM324。

姬安召，男（1983-），讲师，主要从事油气藏数值模拟工作。