基于三轴加速度传感器的步长估算模型研究

刘 雷， 慕艳艳， 刘睿鑫

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)



基于三轴加速度传感器的步长估算模型研究

刘 雷， 慕艳艳， 刘睿鑫

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)

估算步长是行人航位推算系统的重要一环，直接影响行人当前位置的推算结果。提出了一种基于三轴加速度传感器的步长估算模型，用于室内、外行人步长的估算。采用微机电系统(MEMS)低功耗三轴加速度传感器采集行人的运动信息，根据运动加速度的曲线特点，经过信号去噪、剔除异常采样点等预处理，提取相应的步频、加速度峰值关键特征，建立步长估算的数学模型。实验结果表明：该数学模型估算的步长误差在2 cm以下，具有良好的准确性和稳定性。

三轴加速度传感器； 步长估计； 步频； 数学模型

0 引 言

在全球定位系统(GPS)不可得的环境中，基于微机电系统(MEMS)惯性传感器进行行人航位推算是一种很好的选择，具有短时高精度、低功耗的特点[1]，可以用于室内、煤矿井下等环境中的航迹推算。

在进行行走航迹推算时，建立准确的行人步长估算模型至关重要。目前，常用的步长估计模型有常数步长模型、线性步长模型、非线性步长模型、神经网络模型。文献[2，3]采用常数步长模型，算法简单，使用方便，但无法反映步长变化的随机性。文献[4]基于步频估算步长，进一步提高估算精度。文献[5，6]利用加速度的四次方根估算步长，只需求解一个参数，但行走步频改变时，估算误差较大。文献[7，8]采用神经网络模型估算步长，适应于不同斜度的地面状况，灵活性强，但对GPS定位有很大的依赖。

本文基于三轴加速度传感器提出了一种新的步长估计模型，用于GPS不可得的煤矿井下提高人员定位系统的定位精度。构建以三轴加速度传感器CJMCU-250E BMA250E BOSCH、Edison处理器模块为核心的实验装置，进行行人步长实验测试研究。根据不同行人、不同速度相应的加速度曲线特性，平滑滤波、剔除异常采样点等预处理后，获取步频、加速度峰值关键特征，建立步长估算的数学模型。该模型能较好地反映不同行人的步态特征。

1 实验与测试数据

本文设计开发了基于MEMS加速度传感器的步长测量装置，硬件系统结构如图1所示。传感器模块选用MEMS低功耗三轴加速度传感器CJMCU—250E BMA250EBOSCH，测量范围为±2gn，分辨率为6.1×10-5gn，模块内集成有数字滤波器，测量精度高。CPU采用Intel Edison计算机模块；模块采用Inter Atom处理器，集成了12位高速A/D转换器；测量装置运行Linux系统，采用C语言进行了数据采集软件开发，测量数据存储在Intel Edison的1 GB存储器中，实验结束通过串行端口上传到计算机，数据处理使用Matlab。测量时装置佩戴于测试者腰部。

图1 硬件系统结构

行人自然步行的频率为75～125步/min，普通人的步长分布在50～90 cm范围[9，10]，因此，行走的速度范围为0.7～1.8 m/s，即步行的频率为1.25～2.08 Hz，根据采样定理，采样频率取30 Hz，保证信息不丢失。

本文对不同步速对步长的影响进行了研究[11,12],测试者分别以不同速度进行了42组行走测试。每次测试均对加速度传感器进行校正处理[13,14]，实验测得行走速度分别为0.70,0.80,1.20,1.32,1.65,1.70,1.80 m/s。测试场地为一直行走廊，行走距离为40 m。每组测试数据的时间、步数及合成加速度峰值如图2所示。

图2 行人行走测试数据

2 数据处理与分析

2.1 数据滤波处理

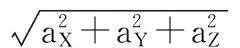
图3 窗口长度取不同值时的滤波效果

滑动窗口长度取n=8时，如图3所示，能够剔除加速度信号里的高频噪声，因身体抖动造成的多峰值波形也被平滑成单峰值，便于峰值探测。合加速度asum在中值滤波前、后的波形如图4所示。

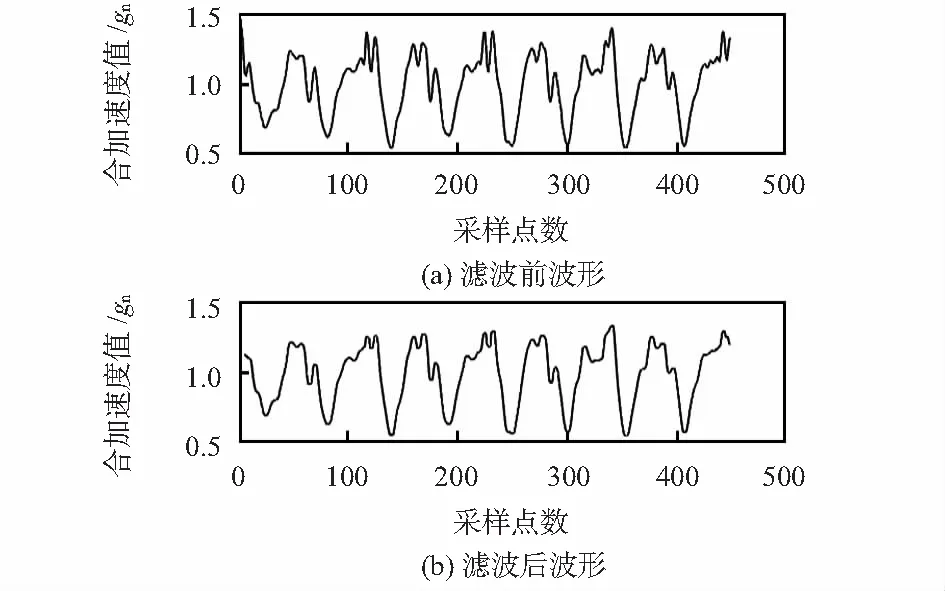
图4 预处理前、后的波形

2.2 数据处理

图4(b)表明：滤波后的合加速度波形呈周期性变化，符合人体行走的步态规律，相邻波峰之间对应一个完整的步态周期，即两步。平滑的波形曲线便于波峰检测、峰值获取以及相邻波峰之间采样个数计数。从图5可以看出，加速度峰值越大，相邻波峰间的采样个数越少。根据采样频率30Hz，实时计算步频。综合步频、合加速度因素，建立并优化步长估算模型，实时估算步长。

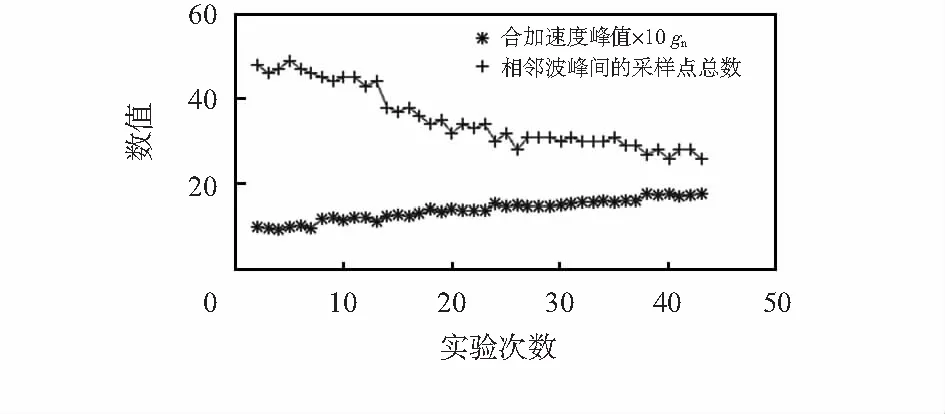
图5 合加速度峰值与相邻波峰间采样点总数对应关系

3 步长数学模型

3.1 步长与步频、合加速度的关系

记步频F,步数N，步长L，行走的距离为D，采样频率H，相邻波峰之间的采样个数为M，则有下述关系

F=2H/M= N/t

L=D/N

(1)

式中 t为行走距离D所用的时间。利用Matlab可得步长L、步频F、合加速度asum之间的关系图，如图6所示。

图6 步长L与合加速度asum、步频F的对应关系

3.2 步长数学模型的建立

图6表明：随着合加速度asum、步频F的变化，步长L 呈正相关变化，近似线性增大或减小。因此，L关于F，asum的线性关系方程有

L=A asum+BF+C

式中 A，B，C为模型待求参数。理论上，asum，F同时为零时，人应处于静止状态，L=0,即参数C=0。考虑到现实环境中行走步态的复杂性，本文建立具有普适性的步长估计模型。

利用Matlab对测试数据进行线性拟合，拟合结果如图7所示。表明，‘·’点群与‘*’点群并没有完全重合，少许点之间存在着残差。

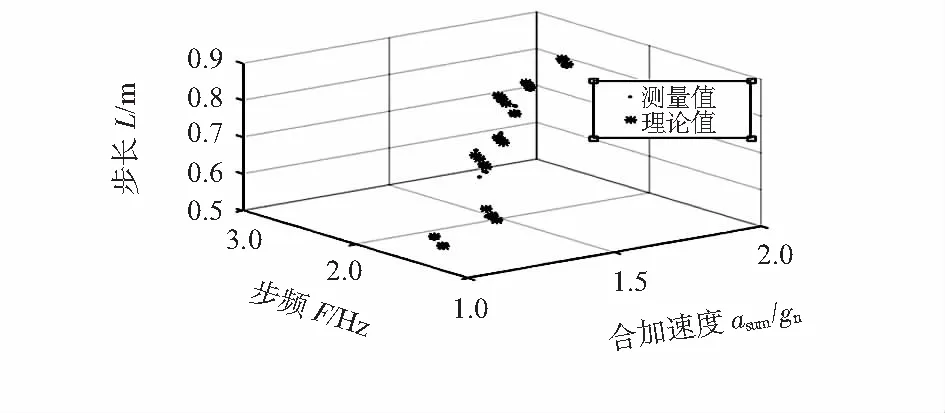
图7 测量值与理论值的比对

利用Matlab进行回归计算，求得步长模型

L=0.132asum+0.123F+0.225

(2)

相关系数r2=0.928，数学模型较好地符合原始数据。图8表明所有数据的残差离零点均较近，且残差的置信区间均包含零点。其中，每条线长度为置信区间，小圆圈为残差点。

图8 拟合结果的残差分析

3.3 数学模型验证与比较

对于模型(2)进行模型的验证和比较研究，选取了测试者6名，3名男性，3名女性，女性身高分别为158，164，168cm；男性身高分别为170，175，181cm。测试场地仍为原场地，行走距离分别为30，35，40，45，50m。设计实验距离依据所研究的模型主要用于2个基站之间的距离估计。每个测试者行走以上5个距离1次，共进行了30组实验。对比模型采用式(3)

SL=MF+N

(3)

式中 M，N为模型系数；F为步频。

步长测试结果如图9所示。表明：随着行走距离的增大，2种数学模型的估算距离与实际行走距离之间的偏差逐渐变大，这是步长估算误差累计的结果，且“*”偏离“☆”较远，表明数学模型SL产生的误差较大。

图9 2种步长模型测试结果对比

3.4 误差分析

2组数学模型的步长估算误差如表1所示。

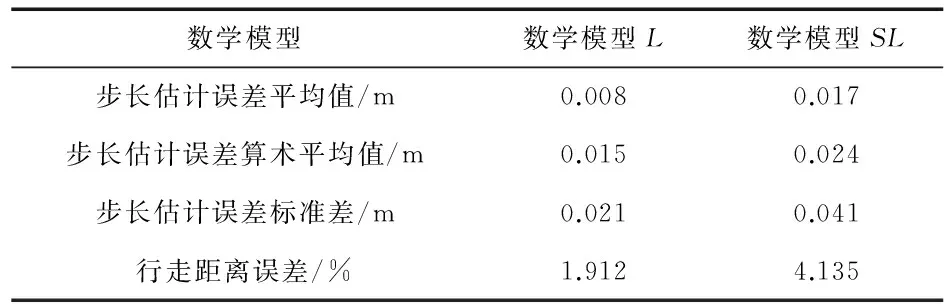
表1 2种数学模型测试结果

表1表明数学模型L的步长估算误差比较集中，在2 cm以下，稳定性好，准确度高。

4 结 论

本文提出一种基于三轴加速度传感器的步长估算模型，用于室内、外行人步长的精确估算。设计的可穿戴行人步长实验装置佩戴于测试者腰部，CPU选用Intel Edison计算机模块、采用MEMS低功耗三轴加速度传感器模块。详细介绍了步长测试实验的方法、测试数据的处理分析、数学模型的建立及优化、相关步长数学模型的对比分析。室内测试结果表明：该步长模型综合考虑合加速度峰值、步频双重因素，能够体现出不同行人、不同频率的步态随机性，步长估算误差在2 cm以下，具有良好的准确性和稳定性，进一步提高了煤矿井下人员定位的精度。

[1] 李旭辉.MEMS发展应用现状[J].传感器与微系统,2006,25(5):7-9.

[2] 宣秀彬．基于WiFi和航位推算的室内定位方法研究[D]．秦皇岛：燕山大学，2013.

[3] 刘志达．智能手机室内定位技术的研究与实现[D]．广东：华南理工大学，2015.

[4] 李金凤，王庆辉，刘晓梅，等．基于MEMS惯性传感器的行人航位推算系统[J].传感器与微系统，2014,33(12)：85-87，90．

[5] 徐 伟．基于Android手机的室内定位技术研究与实现[D]．武汉：华中师范大学,2014.

[6] 张 迅，黎 伟，周建国，等．基于传感器的室内测试轨迹系统[J]．传感器与微系统，2015,34(6):43-45，49.

[7] Altun K,Barshan B.Pedestrian dead reckoning employing simultaneous activity recognition cues[J].Measurement Science and Technology,2012,23(2):025103.

[8] Prieto J,Mazuelas S,Bahillo A,et alPedestrian navigation in harsh environments using wireless and inertial measurements[C]∥2013 10th Workshop on Positioning Navigation and Communication(WPNC),IEEE,2013.

[9] 李若涵,张金艺,徐德政,等.运动分类步频调节的微机电惯性测量单元室内行人航迹推算[J].上海大学学报：自然科学版,2014(5):612-623.

[10] 练艺影,王正珍,李雪梅,等.20～59岁年龄段普通成年人健步走推荐速度及步频的研究[J].北京体育大学学报,2012(7):49-51，57.

[11] 安 宇.论步频和步长的关系[J].牡丹江大学学报,2008(1):125-127.

[12] 费程羽,苏 中,李 擎.行人惯性导航零速检测算法[J].传感器与微系统,2016,35(3):147-150，153.

[13] 林生荣,张 辉.三轴加速度传感器校正方法研究[J].传感器与微系统,2011,30(11):72-74，78.

[14] 王建东,刘云辉,樊玮虹,等.MEMS传感器的惯性测量模块的设计与初始校准[J].传感器与微系统,2006,25(10):82-85.

[15] 齐保振.基于运动传感的个人导航系统及算法研究[D].杭州：浙江大学,2013.

[16] 韩文正,冯 迪,李 鹏,等.基于加速度传感器LIS3DH的计步器设计[J].传感器与微系统,2012,31(11):97-99.

[17] 张建平.基于WiFi的室内定位系统设计和算法研究[J].自动化技术与应用，2016,35(12)：53-57.

[18] 洪雁，王培康.基于稀疏表示多分类的室内定位算法[J].无线电工程，2014,44(2)46-49.

Research on model for step length estimating based on tri-axis acceleration sensor

LIU Lei， MU Yan-yan， LIU Rui-xin

(School of Mechanical Electronic and Information Engineering,China University of Mining and Technology(Beijing),Beijing 100083,China)

Estimating step length is an important part of pedestrian dead reckoning system,directly affects the calculation result of the pedestrian’s current position.Based on tri-axis acceleration sensor,model for estimation of pedestrian’s step length is proposed indoor and outdoor.Hardware platform utilize low power tri-axis MEMS acceleration sensor is used to collect the pedestrian’s movement information consumption,which containing key characteristics of step frequency and the peak of acceleration according to features of the motion acceleration curve.After signal denoising and eliminating the abnormal sampling points,a mathematical model for measuring step-length is built.Related experiments show that the mathematical model has better accuracy and stability and the calculation error is less than 2 cm at every step.

tri-axial acceleration sensor; step estimation; step frequency; mathematical model

10.13873/J.1000—9787(2017)08—0022—03

2016—09—01

TP 212

A

1000—9787(2017)08—0022—03

刘 雷(1989-)，男，硕士研究生，主要研究方向为传感器应用，模式识别。