基于QCM的湿度传感器等效电路模型研究*

郭剑锋， 刘庆辉， 郑国恒， 杨 洁， 时朝晖

(郑州大学 物理工程学院，河南 郑州 450001)



基于QCM的湿度传感器等效电路模型研究*

郭剑锋， 刘庆辉， 郑国恒， 杨 洁， 时朝晖

(郑州大学 物理工程学院，河南 郑州 450001)

基于石英晶体微天平(QCM)的湿度传感器是一种以石英晶体为核心元件的新型高灵敏度传感器。根据气相中晶体振荡电路的起振和稳定条件，对晶体表面敏感薄膜吸附水分时等效电路参数的变化进行建模，得到了一种新型的基于QCM的湿度传感器等效电路模型。通过电路仿真软件PSPICE对模型进行仿真，并搭建QCM湿度传感器实验测量平台，结果验证了基于QCM的湿度传感器等效电路模型的有效性和正确性，对QCM湿度传感器的振荡电路的进一步设计和优化具有指导意义。

石英晶体微天平； 湿度传感器； PSPICE仿真； 等效电路模型

0 引 言

石英晶体微天平(quartz crystal microbalance，QCM)是一种可以将石英晶体电极表面ng级的质量的改变转换为可测量的振动频率的改变[1]。QCM以其较高的质量灵敏度被广泛用于电化学、生物医学、分析化学和物理学等研究领域[2]。QCM信号采集主要有3类方法：耗散因子法、频谱分析法和振荡电路法[3]。耗散因子法通过检测流过晶体的衰减电流得出串联谐振频率和耗散因子D，缺点是激励信号产生困难;频谱分析法通过分析QCM输出信号的幅度和相位来获得晶体的串并联谐振频率、晶体阻抗等电学参数，缺点是电路设计复杂且实时性差;振荡电路法设计成本低，实时性强，能够产生稳定的正弦频率信号[4]。本文采用了振荡电路法设计QCM湿度传感器的接口电路[1,5,6]。

湿度传感器以石英晶体为谐振元件，表面涂覆的湿敏薄膜为敏感元件。本文对晶体表面敏感薄膜吸附水分时等效电路参数的变化进行建模，利用PSPICE软件对模型进行仿真，通过实验测量得到振荡频率与空气湿度的变化关系，对模型进行验证。

1 石英晶体的电气特性

1.1 晶体等效电路模型

晶体振荡频率接近机械谐振频率时，石英晶体模型(Butterworth-van-Dyke，BVD)的等效电路如图1所示。图中石英晶体被看作一个被电容C0分路的LRC串联谐振电路[6,7]，包括4个主要参数：静态电容C0、动态电容C、动态电感L及动态电阻R。

图2给出了一个10 MHz石英晶体在谐振频率附近时的阻抗和相位特性曲线，其中实线段表示阻抗特性，虚线段表示晶体随频率变化时在电路中提供的相位特性。虚线上相位为0°的两点对应横坐标为晶体的谐振频率。

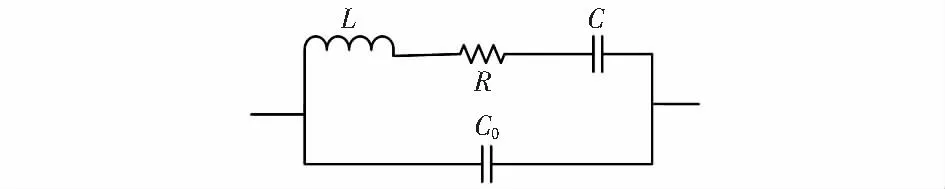
图1 无负载等效电路

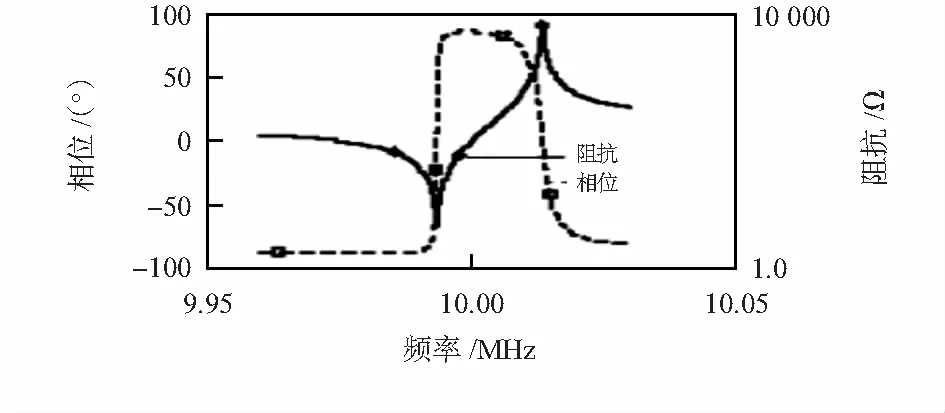
图2 10 MHz石英晶体的阻抗特性曲线

石英晶体的阻抗表达式为

(1)

式中Re和Xe为等效串联阻抗的实部和虚部，Ω;ω为晶体的振荡角频率，rad/s。晶体谐振的条件为Xe=0，即

R2ω2C2C0-(ω2LC-1)(ω2LCC0-C0-C)=0

(2)

由于R2ω2C2C0的理论值非常小，可以忽略，由式(2)得到的解ωs和ωp为石英晶体固有两个谐振频率。

1)串联谐振频率fs

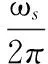
(3)

石英晶体在发生串联谐振时，晶体在电路中产生的相移为0°，呈纯阻性，阻抗最小，约为10 Ω左右。

2)并联谐振频率fp

(4)

石英晶体在发生并联谐振时，晶体在电路中产生的相移为0°，呈纯阻性，阻抗最大。当晶体振荡在串联谐振频率fs和并联谐振频率fp之间时晶体呈感性，产生相移+90°，而在其他频率区间呈容性，产生相移-90°。

1.2 振荡电路平衡条件

以石英晶体为核心元件构成的振荡电路结构可以生成平稳的正弦波频率信号，更容易被数字系统测量分析。这种振荡电路平衡的条件满足巴克豪森准则[7]，可以描述为

1)幅度条件：|kA|≥1。其中，A为开环放大增益；k为反馈放大系数。

2)相位条件：ψ=0,2π,…,2nπ，ψ为环路增益相角。

晶体振荡电路可以归结为两种电路原型：串联谐振和并联谐振。图3(a)中晶体谐振在串联谐振频率上，等效为阻值极小的纯电阻，产生0°的相移，反相放大器产生180°的相移，满足相位平衡条件，被称为串联谐振电路。图3(b)中反相放大器产生180°的相移，反馈回路中R1，C1，C2提供剩余的相位偏移来满足360°的相位平衡条件。电路中，石英晶体呈感性，被称为皮尔斯并联谐振电路。

图3 反相器谐振电路

2 QCM湿度传感器电学模型

2.1 晶体表面薄膜吸收水分的影响

晶体表面薄膜吸附的水分必然会产生附加的并联电容，如图4中的静态电容C0增加C1。由式(3)、式(4)可知并联谐振频率略微减小而串联谐振频率不受影响。水分中掺杂的灰尘和杂质也会改变吸附物的粘稠度，从而使等效电阻R、动态电感L增加[8]。石英晶体等效参数L，C，R和C0引自PSPICE软件Xtal库[9]中的10 MHz晶体谐振器参数：L=2.546 479 09 mH，C=0.099 604 118 1 pF，R=6.4 Ω，C0=24.901 029 5 pF。

图4 石英晶体吸收水分等效电路

图5 L1对晶体相位影响

由式(3)和图5可以看出，晶体等效电感L1的增加，使得串联谐振频率降低，是导致晶体振荡频率变化的主要参数。同时等效电阻的变化R1是决定石英晶体谐振器品质因数Q值的主要因素，根据振荡回路品质因素的定义式

(5)

式中Q为晶体的品质因素；晶体等效电阻R1的增加表示振荡回路损耗的增加，使得晶体在谐振频率附近呈感性时提供的相位下降，晶体振荡电路的相位平衡条件恶化；谐振点处相位曲线斜率下降，影响晶体振荡的稳定性。图6中曲线分别为电阻R1为0，40,80 Ω时晶体提供的相位图。

图6 R1对晶体相位影响

2.2 振荡电路设计原则

在设计QCM湿度传感器的接口振荡电路时，表面薄膜吸收水分的石英晶体能保持稳定振荡需要满足以下条件：1)使晶体在串联谐振频率附近振荡。因为并联电容C0的改变对于串联谐振频率影响很小，其次工作在串联谐振点的晶体阻抗是在射频技术阻抗(50 Ω的波阻抗)的范围内，能够尽量减少干扰信号耦合的影响。2)在振荡回路中增添合适的相位补偿元件。在薄膜表面吸收水分后，晶体在电路中提供的相位降低，导致其不满足电路相位平衡条件。

3 实验验证

3.1 QCM湿度传感器性能测试

石英晶体采用晶华创公司的UM系列中的10 MHz晶体谐振器，通过化学沉积法在石英晶体表面均匀淀积湿敏薄膜，前端电路采用图3(a)所示电路。将一路QCM湿度传感器振荡电路置于密闭容器中，另外一路暴露容器外的空气中作为对比参考，在空气相对湿度为23 %RH时采集得到QCM晶体振荡的频率f0=(9.966 505×106±10)Hz。调节密闭容器内等温加湿器，改变容器中的空气湿度，测量数据通过串口传送到上位机中实时显示并存储，得到实际频率与等效参数关系如表1。

对实验中采集的多组数据进行分析总结，绘制图7所示曲线。横坐标为相对时间，纵坐标为代表密闭容器中不同湿度环境中，石英晶体的振荡输出频率。测量结果表明：附有湿敏薄膜石英晶体的输出频率随着空气湿度的增加而降低。同时，多次检测同一湿度环境下的晶体振荡频率基本保持不变，表明QCM湿度传感器测量具有重复性。

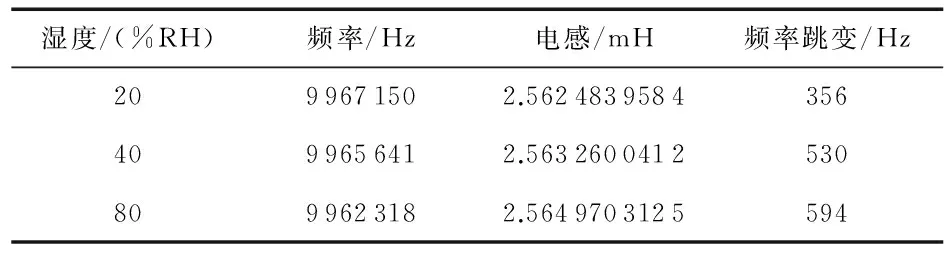
表1 实际频率与等效参数关系

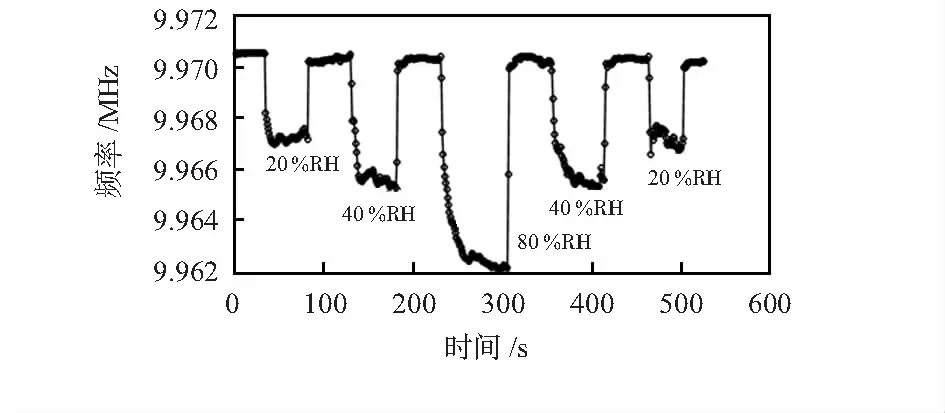
图7 晶体振荡频率随空气湿度的变化曲线

3.2 实验模型验证

QCM湿度传感器在电路中谐振在串联谐振频率上，C0的改变对于串联谐振频率影响很小。由表1，电感值与晶体振荡频率近似呈反比关系，与式(3)相对应。空气湿度增加时，观测到晶体振荡的频率跳变增加，即晶体振荡的稳定性下降。原因是晶体振荡回路中的损耗增加，由品质因数Q的定义知，等效电阻R1的增加使晶体的品质因素降低，导致晶体振荡稳定性的下降。将湿度传感器置于湿度较高(高于80 %RH)的空气中，晶体会出现停止振荡的情况。通过观察图6中相位曲线的变化，等效电阻R1过大致使晶体在电路中提供的相位很小而不满足相位起振条件。解决这一问题的方法就是在振荡回路中增加相位补偿元件，使振荡回路重新满足相位平衡条件。

4 结束语

文中利用石英晶体振荡频率的输出变化实现空气湿度的检测，通过数据分析明确了晶体的等效动态电感是导致晶体振荡频率变化的重要等效参数，等效损耗电阻是决定石英晶体谐振器品质因数Q值和相位稳定的主要因素。该等效电路模型的建立和分析对QCM湿度传感器的振荡电路的设计和改进具有一定的指导意义。

[1] 陈超杰,蒋海峰.石英晶体微天平的研究进展综述[J].传感器与微系统,2014,33(5):5-8,11.

[2] Chen Y Y,Li X D,Chen X Y et al.Investigation of the stability of QCM humidity sensor using grapheme oxide as sensing films[J].Sensors and Actuators B:Chemical,2014,191:779-783.

[3] 肖光华.QCM湿度传感器测量系统的研制[D].哈尔滨:哈尔滨工业大学,2012:20-26.

[4] 周俊鹏，包 宇.新型宽频自适应石英晶体微天平测量方法[J].分析化学,2014,42(5):773-778.

[5] Mumyakmaz B,Ozmen A,Ebeoglu M,et al.A study on the deve-lopment of a compensation method for humidity effect in QCM sensor responses[J].Sensors and Actuators B: Chemical,2010,147(1):277-282.

[6] 稻叶保.振荡电路的设计与应用[M].何希才，尤 客，译.北京：科学出版社，2004:135-142.

[7] 赵声衡，赵 英.晶体振荡器[M].北京：科学出版社，2008:38-57.

[8] Eichelbaum F,Borngraber R,Schroder J,et al.Interface circuits for quartz-crystal-microbalance sensors[J].Review of Scientific Instruments,1999,70(5):25-37.

[9] 朱艳丽,陈 拓.基于CMOS反相器石英晶体振荡电路的PSPICE仿真[J].现代电子技术,2012,35(20):163-166.

[10] 邓志鹏,陈向东.基于OrCAD/PSpice的晶体振荡电路设计仿真[J].现代电子技术,2012,35(14):166-168.

Research of equivalent circuit model for QCM-based humidity sensor*

GUO Jian-feng, LIU Qing-hui, ZHENG Guo-heng, YANG Jie, SHI Zhao-hui

(School of Physical Engineering,Zhengzhou University,Zhengzhou 450001,China)

Quartz crystal microbalance(QCM)-based humidity sensor is a new type of high sensitivity sensor based on quartz crystal as the core element of oscillator circuit.According to the oscillation startup and stable condition of QCM in the gas phase,the model for equivalent circuit parameter changes while senstive film coated on QC absorbing moisture is established,and a new equivalent circuit model for humidity sensor is obtained.The model is simulated to demonstrate the correctness and effectiveness of the model by using PSPICE software,which is carried out by an experimental platform for QCM-based humidity sensor.It will have certain instructional significance on the design and improvement of oscillation circuits of QCM humidity sensor.

quartz crystal microbalance(QCM); humidity sensor; simulation with PSPICE; equivalent circuit model

10.13873/J.1000—9787(2017)08—0029—03

2016—08—22

河南省科技攻关计划资助项目(162102210018)

TP 274

A

1000—9787(2017)08—0029—03

郭剑锋(1991-)，男，硕士研究生，研究方向为物理电子学。