基于焦散线方法的自加速光束设计∗

闻远辉陈钰杰†余思远2)

1)(中山大学电子与信息工程学院,光电材料与技术国家重点实验室,广州 510275)

2)(布里斯托大学电气与电子工程系,布里斯托BS81TR,英国)

基于焦散线方法的自加速光束设计∗

闻远辉1)陈钰杰1)†余思远1)2)

1)(中山大学电子与信息工程学院,光电材料与技术国家重点实验室,广州 510275)

2)(布里斯托大学电气与电子工程系,布里斯托BS81TR,英国)

(2017年6月16日收到;2017年7月17日收到修改稿)

以艾里光束为代表的自加速光束是一类在自由空间中具有弯曲传播特性的新型特殊光束.这类光束因其具有无衍射、自加速和自修复等奇异特性引起了人们的广泛关注,有望应用于光学微粒操控、激光微加工、全光路由和超分辨成像等诸多领域.由于艾里光束只能沿着抛物线的轨迹传播,限制了其在实际应用中的灵活性,因而设计出能够沿着不同轨迹传播的自加速光束是这一研究领域的关键问题,而基于焦散线方法的自加速光束设计是解决该问题的有效途径之一.这一方法是将设计的传播轨迹与光学焦散线联系起来,通过分析形成该焦散线所需的光线簇构造出对应的初始场分布.基于该原理并经过不断发展,不同类型的自加速光束相继得以实现,并且借助维格纳函数还可以同时实现实空间和傅里叶空间的自加速光束设计,为自加速光束的应用提供了更多的可能性.本文对基于焦散线方法的自加速光束设计原理和进展进行全面介绍.

物理光学,自加速光束,焦散线,维格纳函数

1 引 言

一般宏观情况下,光在自由空间中是沿着直线传播的,然而近些年来由于艾里光束的发现,在自由空间中具有弯曲传播特性的新型光束(即自加速光束)引起了人们的极大兴趣和广泛关注.艾里光束是由美国中弗罗里达大学的Siviloglou等[1]于2007年率先在实验上实现的.这一类光束除了与贝塞尔光束一样具有无衍射和自修复等特性外,其最吸引人的地方在于没有任何外界作用的情况下光束能够沿着抛物线的轨迹弯曲传播,而不像贝塞尔光束等绝大多数光束一样沿直线传播.正是由于具备这些奇异特性,基于艾里光束的各种潜在应用相继被提出并在实验上进行了演示,包括光学微粒操控[2,3]、弯曲等离子通道的产生[4]、光子弹[5,6]、激光微加工[7]、全光路由[8]、超分辨成像[9,10],和激光诱导放电[11]等.此外,由于艾里波包只是波动方程的解,并不局限于光学领域,对于表面等离子体波[12-15]、物质波[16,17]、声波[18,19]、水波[20]等各种波动系统也同样适用,因而极大地拓展了艾里波包研究的适用领域.关于以艾里光束为代表的自加速光束这一研究领域的更详细介绍可以参见南开大学Chen课题组[21]和苏州大学Cai课题组[22]近期的综述文章.

本文主要聚焦讨论自加速光束的设计这一问题.由于艾里光束只能沿着抛物线的轨迹弯曲传播,这在实际应用中缺乏足够的灵活性,因而设计其他不同轨迹传播的自加速光束一直以来是这一研究领域的一个关键问题.其中一个解决思路是继续寻找波动方程中对应艾里光束以外的其他解析解.在这一思路指导下,在非傍轴情况下沿着圆形、椭圆形和抛物线轨迹传播的半贝塞尔光束[23]、马修光束和韦伯光束[24]以及在三维空间中沿着球体、椭球体传播的亥姆霍兹型光束[25]相继被发现.然而要想继续寻找到沿着其他轨迹传播的自加速光束则变得愈加困难.相比之下,另一个更为有效的解决思路则是基于光学焦散线的方法.这种方法是将设计的光束传播轨迹与光学焦散线[26,27](即光线簇形成的包络)联系起来,它最早是由Green field等[28]提出,在傍轴近似下可以构造出沿着任意二维凸轨迹传播的自加速光束.随后不久,Froehly等[29]将这一方法拓展到非傍轴情况下,从而可以实现大角度的弯曲传播,但还是仅限于二维凸轨迹的情况.在此之后,基于焦散线方法设计的自加速光束类型不断得到拓展,包括从凸轨迹拓展到非凸轨迹[30]、从二维轨迹拓展到三维轨迹[30,31]、从单一主瓣拓展到多个主瓣[32]等.本文对基于焦散线方法设计自加速光束的理念及实现进行讨论.

2 基于焦散线的自加速光束设计原理

2.1 傅里叶空间设计自加速光束

在自由空间中,对于线偏振光,光场的传播满足亥姆霍兹方程,其通解可以表示为沿不同方向传播的平面波叠加的角谱衍射积分形式：

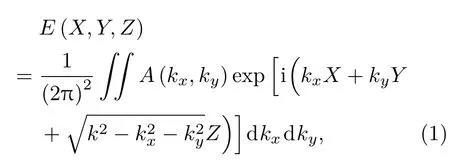
其中A(kx,ky)≡P(kx,ky)exp[i·Φ(kx,ky)]是初始场分布的空间频谱,光场的传播完全由这一傅里叶空间的角谱决定.为了简化起见,下面主要讨论二维情况,即光场不随Y方向变化的情况(三维情况的讨论将在3.3节中给出),此时角谱衍射积分可以简化为

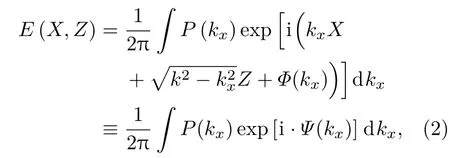
其中E(X,Z)为二维平面(X,Z)的场分布,P(kx)和Φ(kx)为则为初始角谱的振幅和相位分布.如果相位部分exp[i·Ψ(kx)]振荡足够快而振幅P(kx)变化相对比较缓慢,衍射积分的主要贡献将来源于相位函数的驻相点附近对应相位变化较为缓慢的地方,而其他点的贡献则由于相位的快速振荡倾向于相互抵消,即所谓的驻相近似[33](这里称为一阶驻相近似),其中驻相点对应于相位函数的一阶导为零：

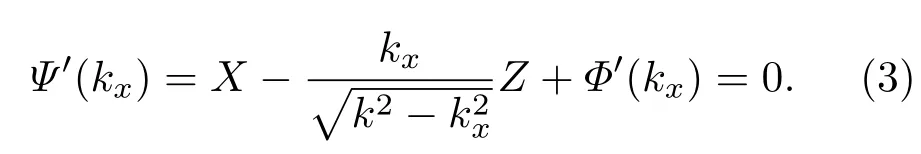
对于固定的空间频率kx,方程(3)是关于空间坐标X和Z的直线方程,对应于几何光学里的一根光线,因而在一阶驻相近似下,光场可以近似用光线簇进行描述,如图1(a1)所示.进一步地,如果令相位函数的二阶导也为零,

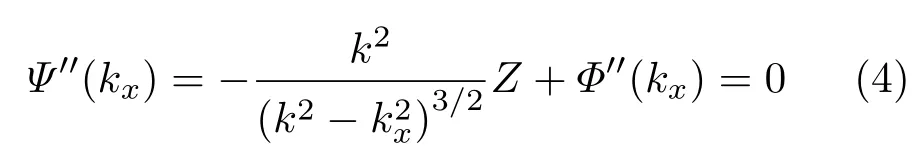
将对应二阶驻相近似.通过联立(3)式和(4)式可以得到空间坐标X和Z之间的关系,即确定出二维平面内的一条曲线X=f(Z),并且该曲线满足：

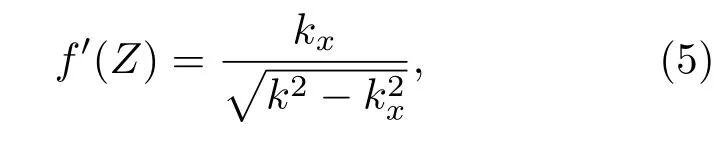
即曲线上每一点都与光线相切,表明该曲线实际上是光线簇所成的包络,如图1(a2)所示.如果进一步要求Ψ′′′(kx)=0,则可以确定出空间内的一点(X,Z)=(Xf,Zf),此时所有光线都将经过这一点,对应于光束聚焦的情况,如图1(a3)所示.通过对比可以看到,图1(a2)实际上是光场没有完全聚焦到一点上,而是由于散焦聚焦到一条线上的情况,这样一条曲线称为焦散线.由于在焦散线上相位函数的一阶导和二阶导均为0,因此可以保证在焦散线附近的光强具有极大值.如果将自加速光束的弯曲轨迹与焦散线联系起来,通过焦散线的设计就能得到光束主瓣沿着不同弯曲轨迹传播的自加速光束,这就是基于焦散线方法设计自加速光束的基本思路.从(4)式和(5)式可以看到,给定自加速光束的弯曲轨迹X=f(Z),对应所需的初始角谱的相位函数Φ(kx)即可得到.进而通过对入射光束调制上这一相位分布并由透镜做傅里叶变换即可产生出设计的自加速光束.

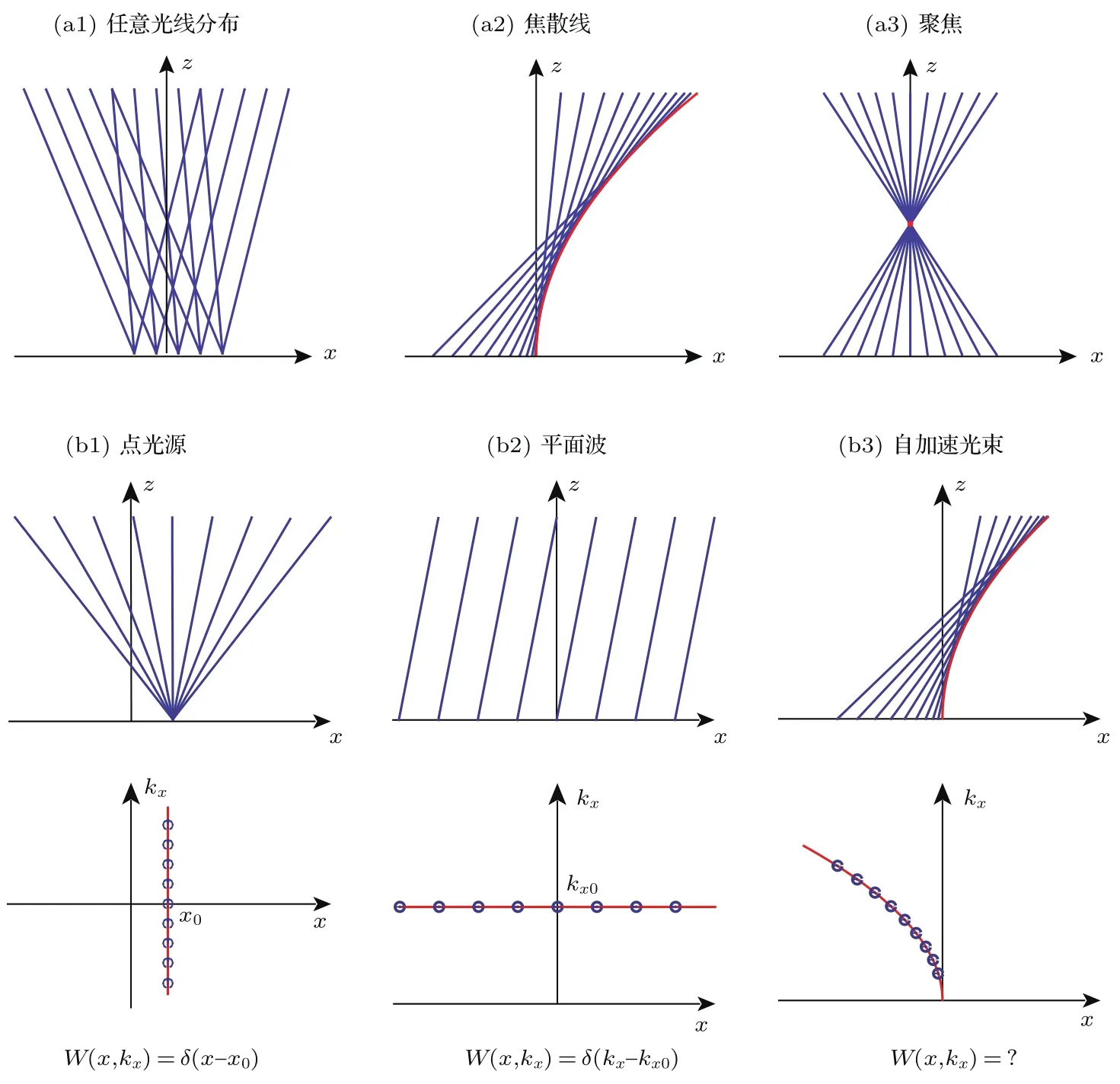
图1 (a1)—(a3)空间光场在不同阶驻相近似下的光线描述;(b1)—(b3)对于点光源、平面波和自加速光束的光线描述和对应相空间的维格纳函数Fig.1.(a1)–(a3)Light-ray description of the light field under the stationary phase approximation in di ff erent orders;(b1)–(b3)light-ray description and the corresponding form of the WDF in phase space for a point source,a plane wave,and a self-accelerating beam.

2.2 相空间设计自加速光束

以上基于焦散线方法设计自加速光束是从傅里叶空间的角谱衍射积分出发进行分析的,类似地也可以从实空间的菲涅耳衍射积分出发进行分析[28].在傅里叶空间和实空间构造自加速光束原则上是等价的,但对于实际产生自加速光束则各有优点.基于傅里叶空间的构造方法是在傅里叶平面对光场进行调制,然后再经过一个透镜做傅里叶变换产生出自加速光束,由于产生自加速光束的平面是光场调制平面的远场,因而实际中调制平面的离散化以及相位调制的细微偏差对光束质量的影响较小,光束主瓣在传播过程中的强度变化也相对均匀.而基于实空间的构造方法则是直接在实空间对光场进行调制,由于调制平面即是自加速光束传播的初始平面,经过调制平面后直接就产生出自加速光束,因而光路相对紧凑,有利于进一步的集成.而最近的研究发现[31],这两种在实空间和傅里叶空间设计自加速光束的方法可以统一到在相空间构造维格纳函数的方法中去.这一方法的设计思路是通过类比点光源和平面波的情况,根据焦散线确定出构造自加速光束所需的光线簇,其中每一根光线具有特定的初始坐标x和方向kx,对应于相空间内的一点(x,kx),如图1(b)所示,由此可以构造出相应的维格纳函数：

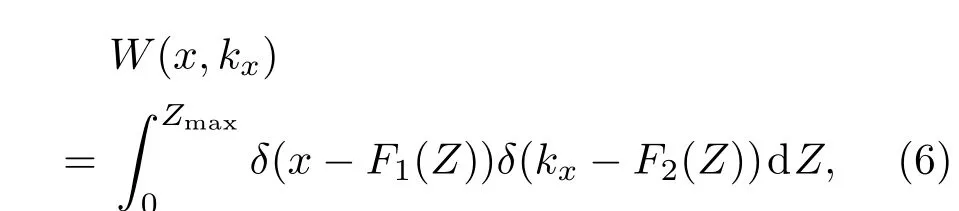
其中Zmax是设计的弯曲传播轨迹的最远距离, F1(Z)=f(Z)-Z·f′(Z),F2(Z)=k·f′(Z).利用维格纳函数的性质即可得到所需的初始场分布E(x)=ρ(x)exp[i·φ(x)]和角谱A(kx)= P(kx)exp[i·Φ(kx)].

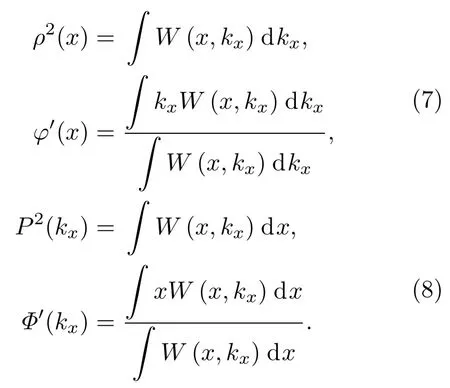
3 不同类型的自加速光束设计

3.1 二维情况下沿凸轨迹传播的自加速光束

利用焦散线方法最先实现的是沿着任意凸轨迹传播的自加速光束[28],其中典型的代表则是沿着幂律轨迹X=f(Z)=anZn(an＞0,n＞0且 /=1)传播的情况.根据前面的理论分析可以推导出其在实空间和傅里叶空间对应的初始场分布也为相应的幂函数：

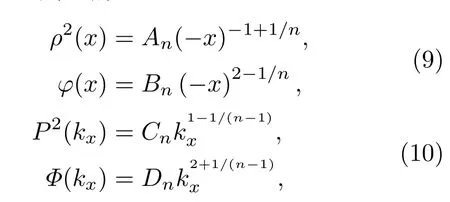
其中An,Bn,Cn,Dn为特定系数.图2所示为其中n=3,2和3/2的三个例子,虚线对应的是相应幂函数的焦散线.可以看到,光束的主瓣是沿着这一设计的轨迹弯曲传播的.值得注意的是,在傅里叶空间设计的n=2的情况实际上对应的就是艾里光束.

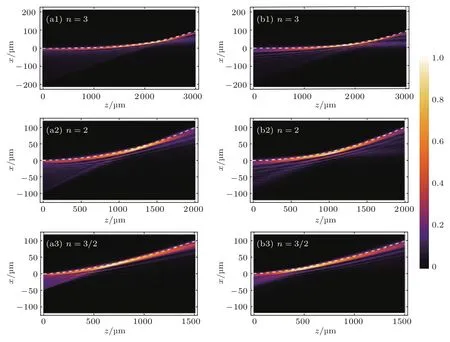
图2 沿着幂律轨迹传播的自加速光束的光强分布图,其中指数n取3,2和3/2作为示例,这里自加速光束分别通过(a1)—(a3)实空间的初始场分布和(b1)—(b3)傅里叶空间的角谱构造得到,其中设计的传播轨迹在图中用虚线表示Fig.2.Intensity distribution of accelerating beams propagating along power-law trajectories with power n chosen to be 3,2,and 3/2 for demonstration.Accelerating beams are constructed in(a1)–(a3)real space and(b1)–(b3)Fourier space based on the initial field distribution and the angular spectrum,respectively.The predesigned trajectories are depicted by dashed curves.

3.2 二维情况下沿非凸轨迹传播的自加速光束

从(5)式可以看到,只有对于凸轨迹情况,其一阶导才是单值函数,与空间频率kx才能一一对应,从而求解出对应的初始场分布和角谱.因此,先前的研究利用这种基于焦散线方法设计自加速光束仅仅局限于二维凸轨迹的情况,表现为自加速光束只能朝着一个方向弯曲而不能像“S”型曲线那样多次弯曲,如图3(a)所示.而我们在最近的研究[30]中提出的叠加焦散线的方法则可以实现这种沿非凸轨迹传播的自加速光束,其设计的思路是将非凸轨迹在所有拐点处断开成若干段凸轨迹,每一段凸轨迹可以利用前面的焦散线方法得到对应所需的初始场分布或角谱,然后把这些初始场分布或角谱叠加起来：

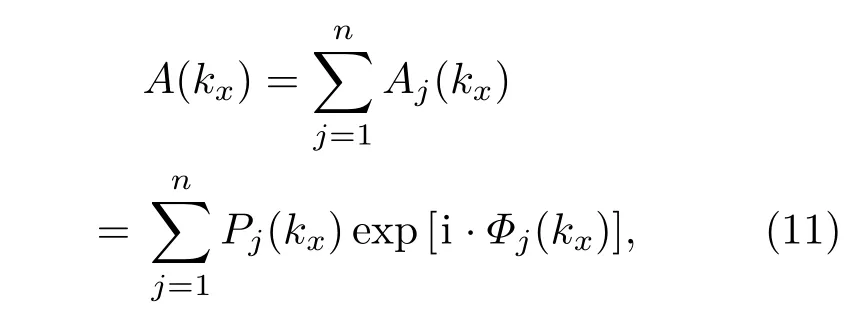
从而实现完整的非凸轨迹传播.值得注意的是,在叠加过程中每段凸轨迹之间的连接处存在π/2的相位差,原因是在一阶驻相近似后得到的光线在经过焦散线后会有π/2的相位改变,进一步的分析详见文献[27].基于这种叠加焦散线方法设计的一种沿着正弦轨迹传播的自加速光束的仿真和实验结果对比如图3(b)和图3(c)所示,可以看到二者符合得非常好,光束主瓣沿着预设的正弦轨迹传播.值得一提的是,图3中自加速光束的产生是基于集成光子技术通过制备微结构对光场波前调控实现的,其中相位调制是通过刻蚀不同深度的台阶得到不同的相位延迟;而振幅调制则是通过蒸镀不同占空比的金属得到不同的透过率,以此获得设计的初始光场分布.相比于传统的基于空间光调制器产生自加速光束的方法,近年来通过光子微纳结构实现精确的光场波前调控进而产生出各类新型光束已成为这一领域的重要发展趋势[34-38],有望实现新型光束产生器件的小型化.

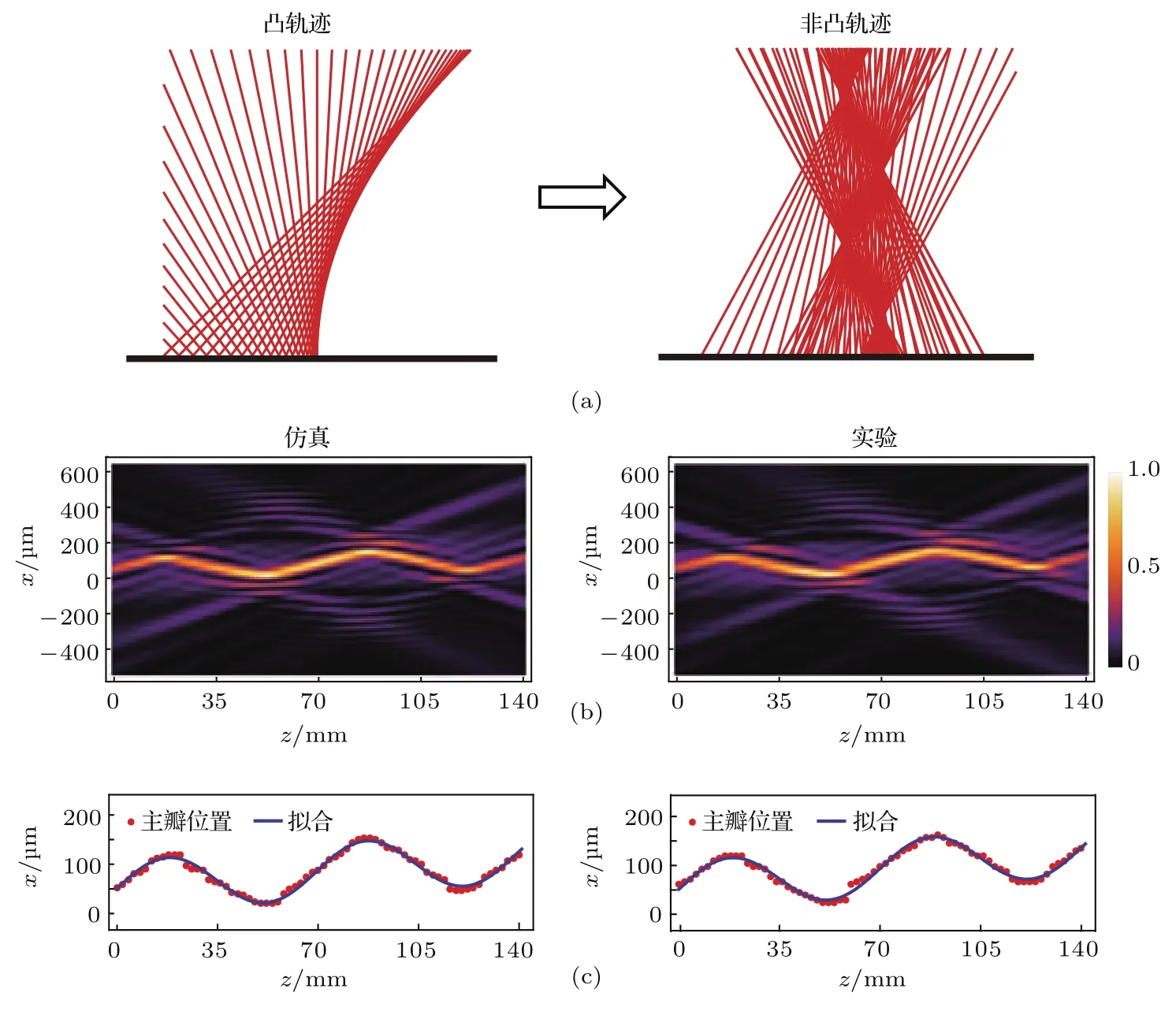
图3 (a)从凸轨迹传播的自加速光束拓展到非凸轨迹的示意图;(b)构造的二维情况下的正弦型光束传播过程中的光强分布的仿真和实验结果对比;(c)光束主瓣传播轨迹的定量分析,其中红色圆点标记的是各个截面光强最大值所在的位置,而蓝色曲线则是拟合出来的轨迹.具体实验及拟合信息详见文献[30]Fig.3.(a)Schematic of the extension of accelerating beams from convex trajectories to nonconvex trajectories;(b)simulated and experimental intensity distribution for the sinusoidal beam propagating in 2D space;(c)quantitative analysis of the main lobe trajectory,here red dots mark the positions of the intensity maxima at the cross sections and the blue curves are the fi tted trajectories.Detailed information can be referred to Ref.[30].

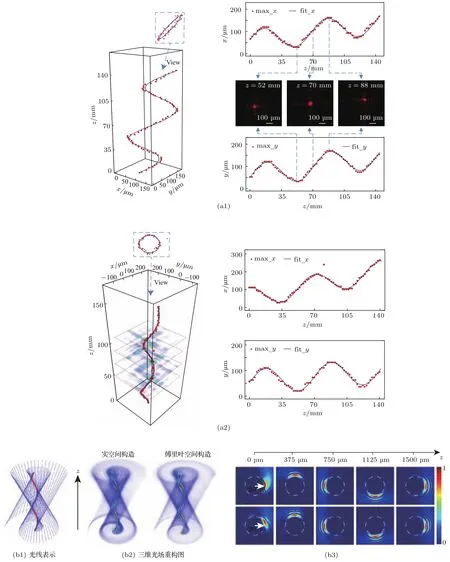
图4 三维空间中的自加速光束设计[30,31]基于二维情况下的Sine型光束合成三维空间中的(a1)Sine型光束和(a2)螺旋型光束;直接通过三维焦散线方法设计螺旋型光束,其中(b1)是光线表示,(b2)和(b3)则是螺旋型光束在传播过程中的三维光场重构图和切片的光强分布图Fig.4.Design of accelerating beams in three-dimensional(3D)space[30,31]：Construction of the Sine beam(a1)and helical beam in 3D space based on the 2D Sine beam(a2);design of helical beams with 3D caustic methods,where(b1)is the light ray representation,while(b2)and(b3)are the 3D tomography and slices of the helical beams during propagation,respectively.

3.3 三维情况下的自加速光束

以上讨论的是二维情况下的自加速光束,即光场分布在Y方向上保持不变,实际上,自加速光束的设计可以从二维情况推广到三维情况.其中一种方法是利用在傍轴近似下的波动方程关于X和Y可分离变量这一性质,将三维情况下的自加速光束设计分解为X和Y两个方向上独立的二维自加速光束设计[30].以图3设计的二维情况下的正弦型自加速光束为例,如果将三维情况下的X和Y方向都设计成正弦型传播轨迹,最终在三维空间中则表现为沿着X轴和Y轴的对角线方向的正弦型轨迹传播,如图4(a1)所示;如果将X方向设计为正弦型轨迹,Y方向设计为余弦型轨迹,最终在三维空间中则是沿着螺旋型轨迹传播,如图4(a2)所示.因而X和Y两个方向通过组合不同的二维自加速光束就可以构造出沿着三维不同轨迹传播的自加速光束.

另一种方法是直接设计三维的焦散线[31,32],考虑一般三维曲线的参数方程：

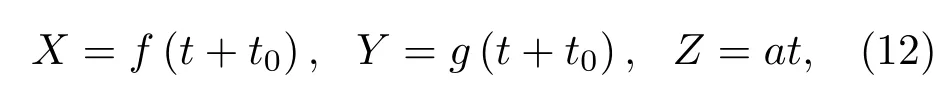
其中t为参数,t0和a为待定参数,通过分析构造该焦散线所需的光线簇,可以构造出相应的维格纳函数：

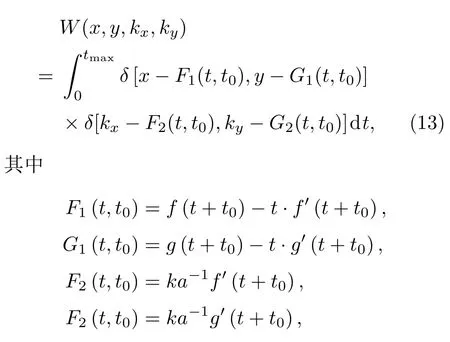
然后利用维格纳函数的性质就能得到对应所需的初始场分布和角谱.基于这种方法设计的螺旋型光束如图4(b)所示.值得一提的是,对于三维自加速光束的设计,除了基于焦散线的设计方法,还有一种基于类贝塞尔光束的设计思路,即将初始场平面分割成足够细的圆周,不同圆周上发出的锥形光线会聚到空间中的不同点[3,39,40].对于贝塞尔光束这些会聚点连成一条直线,因而表现为光束主瓣沿直线传播;而对于类贝塞尔光束则是通过将不同圆周错开,从而得到一条弯曲的聚焦线,表现出光束主瓣沿着弯曲轨迹传播.基于这一方案最早得到的是零阶类贝塞尔螺旋光束[39],在局部保持贝塞尔光束的无衍射性和自修复性下实现了主瓣沿着螺旋轨迹传播.值得注意的是,这一方案还可以进一步将光束的轨道角动量加载上去,实现贝塞尔光束、自加速光束和涡旋光束的结合[3].

3.4 多个主瓣的自加速光束

上述所讨论的自加速光束设计思路中,都是只有一个能量最为集中的主瓣,而实际上主瓣的数目也是一个可供设计的自由度,可以从常见的一个拓展至其他所需的个数,这在一些特定的应用场景比如在光学微粒操控中同时操控不同大小或数量的微粒将非常有用.多主瓣自加速光束的设计可以在单主瓣自加速光束的基础上通过空间上的平移旋转等变换形成若干相互错开的焦散线来实现,图5所示的则是在前面单主瓣螺旋光束的基础上通过这一方法设计出不同主瓣个数的情况[32].由于图5展示的是在弯曲传播的2个周期中沿着传播方向等间距地截取9个截面来反映螺旋光束的传播情况,因而可以看到相邻截面之间螺旋光束主瓣逆时针旋转90°,体现出多主瓣螺旋光束依然保持着很好的螺旋结构,不仅如此,从图5(d)还可以更直观地看到,不同截面的光束主瓣在弯曲传播的同时还保持着高度的相似性,反映出光场主瓣附近具有局部的无衍射特性.

4 结 论

本文介绍了基于焦散线方法设计自加速光束的基本原理,包括从傅里叶空间和实空间的衍射积分出发进行分析以及统一到相空间构造维格纳函数的方法.在此基础上,二维情况下沿任意凸轨迹传播的自加速光束首先得以实现,随后通过不断发展这一焦散线方法,设计得到的自加速光束类型得以不断拓展,包括从凸轨迹拓展到非凸轨迹,从二维轨迹拓展到三维轨迹,从单一主瓣拓展到多个主瓣,为基于自加速光束的各种新应用提供了更多的可能.展望未来,最初基于艾里光束的各种研究和应用必将推广到各类新型自加速光束中,借助自加速光束设计的灵活性,在这个过程中极有可能激发出更多新的应用场景,因而具有极大的发展潜力.

图5 具有不同主瓣个数的螺旋型光束的传播动力学特征[32]图中所示的螺旋型光束包括：(a)1个主瓣,(b)2个主瓣, (c)3个主瓣,(d)4个主瓣;螺旋型传播的周期分别为2018,1970,1917,2087µmFig.5.Propagation dynamics of helical beams with di ff erent numbers of main lobes[32].The helical beams presented include(a)one-lobe,(b)two-lobe,(c)three-lobe,and(d)four-lobe with slightly di ff erent periods of 2018,1970, 1917,and 2087µm,respectively.

[1]Siviloglou G A,Broky J,Dogariu A,Christodoulides D N 2007 Phys.Rev.Lett.99 213901

[2]Baumgartl J,Mazilu M,Dholakia K 2008 Nat.Photon. 2 675

[3]Zhao J,Chremmos I D,Song D,Christodoulides D N, Efremidis N K,Chen Z 2015 Sci.Rep.5 12086

[4]Polynkin P,Kolesik M,Moloney J V,Siviloglou G A, Christodoulides D N 2009 Science 324 229

[5]Chong A,Renninger W H,Christodoulides D N,Wise F W 2010 Nat.Photon.4 103

[6]Abdollahpour D,Suntsov S,Papazoglou D G,Tzortzakis S 2010 Phys.Rev.Lett.105 253901

[7]Mathis A,Courvoisier F,Froehly L,Furfaro L,Jacquot M,Lacourt P A,Dudley J M 2012 Appl.Phys.Lett.101 071110

[8]Rose P,Diebel F,Boguslawski M,Denz C 2013 Appl. Phys.Lett.102 101101

[9]Jia S,Vaughan J C,Zhuang X 2014 Nat.Photon.8 302

[10]Vettenburg T,Dalgarno H I C,Nylk J,Coll-Lladó C, Ferrier D E K,Čizár T,Gunn-Moore F J,Dholakia K 2014 Nat.Method 11 541

[11]Clerici M,Hu Y,Lassonde P,Milián C,Couairon A, Christodoulides D N,Chen Z,Razzari L,Vidal F,Légaré F,Faccio D,Morandotti R 2015 Sci.Adv.1 e1400111

[12]Minovich A,Klein A E,Janunts N,Pertsch T,Neshev D N,Kivshar Y S 2011 Phys.Rev.Lett.107 116802

[13]Li L,Li T,Wang S M,Zhang C,Zhu S N 2011 Phys. Rev.Lett.107 126804

[14]Zhang P,Wang S,Liu Y,Yin X,Lu C,Chen Z,Zhang X 2011 Opt.Lett.36 3191

[15]Epstein I,Arie A 2014 Phys.Rev.Lett.112 023903

[16]Voloch-Bloch N,Lereah Y,Lilach Y,Gover A,Arie A 2013 Nature 494 331

[17]Efremidis N K,Paltoglou V,von Klizing W 2013 Phys. Rev.A 87 043637

[18]Zhang P,Li T,Zhu J,Zhu X,Yang S,Wang Y,Yin X, Zhang,X 2014 Nat.Commun.5 4316

[19]Zhao S,Hu Y,Lu J,Qiu X,Cheng J,Burnett I 2014 Sci.Rep.4 6628

[20]Fu S,Tsur Y,Zhou J,Shemer L,Arie A 2015 Phys.Rev. Lett.115 034501

[21]Chen Z G,Xu J J,Hu Y,Song D H,Zhang Z,Zhao J Y, Liang Y 2016 Acta Opt.Sin.36 1026009(in Chinese) [陈志刚,许京军,胡毅,宋道红,张泽,赵娟莹,梁毅2016光学学报36 1026009]

[22]Wen W,Cai Y J 2017 Laser Optoelectr.Prog.54 020002 (in Chinese)[文伟,蔡阳健2017激光与光电子学进展54 020002]

[23]Kaminer I,Bekenstein R,Nemirovsky J,Segev M 2012 Phys.Rev.Lett.108 163901

[24]Zhang P,Hu Y,Li T,Cannan D,Yin X,Morandotti R, Chen Z,Zhang X 2012 Phys.Rev.Lett.109 193901

[25]Aleahmad P,Miri M,Mills M S,Kaminer I,Segev M, Christodoulides D N 2012 Phys.Rev.Lett.109 203902

[26]Kravtsov Y A,Orlov Y I 1983 Sov.Phys.Usp.26 1038

[27]Vaveliuk P,Lencina A,Rodrigo J A,Matos O M 2015 Phys.Rev.A 92 033850

[28]Green field E,Segev M,Walasik W,Raz O 2011 Phys. Rev.Lett.106 213902

[29]Froehly L,Courvoisier F,Mathis A,Jacquot M,Furfaro L,Giust R,Lacourt P A,Dudley J M 2011 Opt.Express 19 16455

[30]Wen Y,Chen Y,Zhang Y,Chen H,Yu S 2016 Phys. Rev.A 94 013829

[31]Wen Y,Chen Y,Zhang Y,Chen H,Yu S 2017 Phys. Rev.A 95 023825

[32]Wen Y,Chen Y,Zhang Y,Yu S 2017 Chin.Opt.Lett. 15 030011

[33]Wong R 2001 Asymptotic Approximations of Integrals. (Society for Industrial and Applied Mathematics)p76

[34]Li Z,Cheng H,Liu Z,Chen S,Tan J 2016 Adv.Opt. Mater.4 1230

[35]Pu M,Li X,Ma X,Wang Y,Zhao Z,Wang C,Hu C, Gao P,Huang C,Ren H,Li X,Qin F,Yang J,Gu M, Hong M,Luo X 2015 Sci.Adv.1 e1500396

[36]Li X,Pu M,Zhao Z,Ma X,Jin J,Wang Y,Gao P,Luo X 2016 Sci.Rep.6 20524

[37]Lin J,Wang Q,Yuan G,Du L,Kou S S,Yuan X C 2015 Sci.Rep.5 10529

[38]Dolev I,Epstein I,Arie A 2012 Phys.Rev.Lett.109 203903

[39]Jarutis V,Matijošius A,Trapani P D,Piskarskas A 2009 Opt.Lett.34 2129

[40]Zhao J,Zhang P,Deng D,Liu J,Gao Y,Chremmos I D,Efremidis N K,Christodoulides D N,Chen Z 2013 Opt.Lett.38 498

PACS:42.15.Dp,42.68.Ay,42.30.Lr,42.30.Kq DOI:10.7498/aps.66.144210

Design of accelerating beams based on caustic method∗

Wen Yuan-Hui1)Chen Yu-Jie1)†Yu Si-Yuan1)2)
1)(State Key Laboratory of Optoelectronic Materials and Technologies,School of Electronics and Information Technology,Sun Yat-sen University,Guangzhou 510275,China)
2)(Photonics Group,Merchant Venturers School of Engineering,University of Bristol,Bristol BS8 1UB,United Kingdom)

16 June 2017;revised manuscript

17 July 2017)

Self-accelerating beam is a kind of light beam capable of self-bending in free space without any external potential,of which a typical one is the well-known Airy beam.Such a beam has gained great attention for its extraordinary properties, including nondi ff racting,self-accelerating and self-healing,which may have versatile applications in the delivery and guiding of energy,information and objects using light,such as particle manipulation,micro-machining,optical routing, super-resolution imaging,etc.However,since Airy beam can only propagate along parabolic trajectory,which reduces the fl exibility in practical applications,thus how to design accelerating beam’s propagating along arbitrary trajectory is still a crucial problem in this area.One scheme is to keep on fi nding other analytical solutions of the wave equation besides Airy beam,such as semi-Bessel accelerating beams,Mathius beams,and Weber beams,moving along circular, elliptical,or parabolic trajectories,but it becomes increasingly difficult to fi nd out any more solutions.A more e ff ective solution to this problem is based on the caustic method,which associates the predesigned trajectory with an optical caustics and then obtains the necessary initial field distribution by performing a light-ray analysis of the caustics.This method has been implemented in real space and Fourier space based on Fresnel di ff raction integral and angular-spectrum integral,respectively.It has been found recently that they can be uni fi ed by constructing Wigner distribution function in phase space.Based on the caustic method,accelerating beams were constructed to propagate along arbitrary convex trajectories in two-dimensional space at fi rst.With continuous development of this method,the types of accelerating beams available have been extending from convex trajectories to nonconvex trajectories,from two-dimensional trajectories to three-dimensional trajectories,and from one main lobe to multiple main lobes,which opens up more possibilities for emerging applications based on accelerating beams.In future,previous researches and applications based on Airy beams will certainly be generalized to all these new types of accelerating beams,and owing to the great fl exibility in designing accelerating beams,more application scenarios may emerge in this process with huge development potential.Thus in this paper,we review the principle and progress of the caustic method in designing accelerating beams.

physical optics,self-accelerating beams,caustic,Wigner distribution function

:42.15.Dp,42.68.Ay,42.30.Lr,42.30.Kq

10.7498/aps.66.144210

∗国家重点基础研究发展计划(批准号：2014CB340000)、国家自然科学基金(批准号：11690031,61323001,61490715,51403244)、广州市科技计划科学研究一般项目(批准号：2018)和中山大学高校基本科研业务费青年教师重点培育项目(批准号：17lgzd06, 16lgjc16,15lgpy04,15lgzs095,15lgjc25)资助的课题.

†通信作者.E-mail：chenyj69@mail.sysu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Basic Research Program of China(Grant No.2014CB340000),the National Natural Science Foundation of China(Grant Nos.11690031,61323001,61490715,51403244),the Science and Technology Program of Guangzhou,China(Grant No.2018),and Sun Yat-sen University Fundamental Research Funds for the Central Universities of China(Grant Nos.17lgzd06,16lgjc16,15lgpy04,15lgzs095,15lgjc25).

†Corresponding author.E-mail：chenyj69@mail.sysu.edu.cn