光学超振荡与超振荡光学器件∗

陈刚温中泉 武志翔

(重庆大学光电工程学院,光电技术及系统教育部重点实验室,重庆 400044)

光学超振荡与超振荡光学器件∗

陈刚†温中泉 武志翔

(重庆大学光电工程学院,光电技术及系统教育部重点实验室,重庆 400044)

(2017年3月29日收到;2017年5月24日收到修改稿)

传统光学器件的衍射极限极大地制约了远场超分辨光学系统的进一步发展.如何从光学器件层面突破光学衍射极限瓶颈,实现非标记远场超分辨光学成像,是光学领域面临的巨大挑战.光学超振荡在不依靠倏逝波的条件下,可以在远场实现任意小的亚波长光场结构,这为突破光学衍射极限提供了一条崭新的途径.近年来,光学超振荡现象和超振荡光学器件的相关研究得到了快速发展,在理论和实验上成功地演示了超振荡光场的产生和多种超振荡光学器件,并在实验上展示了超振荡光学器件在非标记远场超分辨光学显微、成像以及超高密度数据存储等应用领域的巨大优势和应用潜力.本文对光学超振荡相关理论、超振荡光学器件设计理论和方法、超振荡光学器件发展现状、超振荡光场测试方法以及超振荡光学器件的应用等方面进行详细介绍和分析.

超振荡,超分辨,衍射器件,亚波长

1 引 言

由于光学器件衍射效应的限制,传统光学系统空间分辨率无法突破理论分辨率极限0.5λ/NA(其中λ为波长,NA为光学系统数值孔径)[1],严重地制约了超高分辨光学系统的研制和发展[2].突破衍射极限制约,实现超分辨光学聚焦与成像,对超分辨光学显微[3,4]、超高密度数据存储[5]、纳米光刻[6]、生命科学[7,8]等领域意义重大.1982年,Pohl等[9]研制出第一台基于物体表面隐失波的扫描近场光学显微镜,实现了可见光波段的超分辨光学显微.然而,近场成像仅限于样品表面,无法满足远场超分辨成像应用的需求.荧光单分子定位[10]、光激活定位显微[11]、随机光学重构显微[12]和受激发射损耗显微技术[13]等,可以实现远场超分辨成像.然而,这些技术均依赖于荧光标记.结构光照明显微技术[14]通过空间频率调制获取物体表面光场的高频分量,实现超分辨光学图像重构,可以将极限空间分辨提高一倍.采用双曲超透镜的显微技术[15],分辨率可达到34 nm[16].然而,被检测样品需要尽可能地靠近超透镜内表面,极大地限制了其应用.在光刻中,采用表面等离激元器件[17]可实现80 nm线宽的近场光刻.基于双光子吸收的双光束光刻技术[6],横向分辨率和特征尺寸可分别达到52和9 nm.尽管这些技术都实现了光学超分辨,然而,在实际应用中都具有一定的局限性,如：工作距离远小于一倍波长、需要对样品进行标记、采用非线性材料等.更为重要的是,构成远场成像光学系统的光学器件自身就是衍射受限的.因此,如何从光学器件层面突破衍射极限瓶颈,实现非标记远场超分辨成像,是光学领域面临的重大挑战.光学超振荡基于光的远场传播规律,为突破衍射极限提供了崭新的思路.近年来,光学超振荡现象、超振荡光学器件和超振荡光学显微技术等相关研究得到了快速的发展.特别是光学超振荡在非标记远场超分辨光学显微(分辨率无理论极限)[18,19]和二维、三维超分辨率图像重建等[20]方面,已经显示出巨大的优势和应用潜力.同时,光学超振荡理论、超振荡光学器件及其应用等方面的研究也面临巨大挑战.本文分别对光学超振荡相关理论、超振荡光学器件设计理论和方法、超振荡光学器件的发展现状、超振荡光场测试方法以及超振荡光学器件的应用等方面进行详细介绍.

2 光学超振荡现象

光学超振荡[21]是指由空间频率较低的光场相干叠加,在空间形成局域快速振荡光场的现象.该局域振荡频率可以远大于光场最高空间频率,并在局域空间形成最小特征尺寸小于光学衍射极限的光场分布[22].

以(1)式为例,函数F(x)由Nmax个谐波线性叠加而成.这些谐波可以被看作是一系列具有不同传播方向(kx,kz)的相干平面波,而函数F(x)即为这些平面波相干叠加所形成的衍射光场.第n个平面波在x轴方向的空间频率为kx=2πnv0、复振幅为an,最高次谐波对应的空间频率为2πNmaxv0.如图1所示[21],通过合理设计这些平面波的复振幅an,可以使该衍射光场F(x)在空间局部的振荡(实线)远快于最高频率谐波cos(2πNmaxv0x)(虚线).由于超振荡光场是由传播波相干叠加而成,因此,超振荡光场的形成并不局限于近场区域,而且理论上可以在远场实现任意小的光场结构[23].

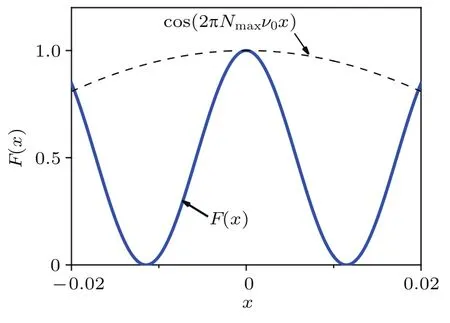
图1 超振荡示意图[21]超振荡函数F(x)(实线)与其所含的最高频率分量(虚线)Fig.1.Schematic of super-oscillation[21]：a superoscillation function(solid line)and its highest frequency component(dashed line).

1952年,Toraldo di Francia[23]提出,超向天线的概念可以应用于光学系统,实现超越衍射极限的光学分辨率.1969年,Frieden[24]指出,一个有限孔径的光学系统,理论上可以通过镀膜的方式在有限区域实现任意完美成像.1985年,Buckelew和Saleh[25]证明可以在衍射受限系统的输出中,构建具有任意分辨率的一维图像.21世纪初,实现不依赖于倏逝波的超分辨思想在光学领域再度复苏[26],光学超振荡为实现这种远场超分辨提供了一种可能的途径.超振荡[27,28]这一概念最早出现在量子力学的弱测量概念中：在空间局部测量获得的光波波数值,可能并不存在于空间整体测量结果的范围内.2006年,Berry和Popescu[29]首次将量子超振荡和光学超分辨联系起来,并从理论上证明在不依赖于倏逝波的情况下,光场中小于波长的超振荡精细结构可以在远场传播,而且其传播距离远大于通常的近场传播距离.2017年,Makris等[30],通过严格求解麦克斯韦方程,得到了基于矢量贝塞尔光束超振荡叠加解的具体形式,再次证明了超振荡光场中的亚波长结构可以被传播到远场区域.根据Ferreira和Kempf[31]的研究结果,产生超振荡光场所需的能量将随着超振荡数目的增加呈指数增长;而随带宽的倒数呈多项式增长.2007年,南安普顿大学Zheludev研究团队[21,32]采用660 nm单色光照射准周期纳米金属孔阵列屏,在距离金属孔阵列屏约19λ处的衍射光场中观测到尺寸为0.44λ的亮斑,首次在实验上演示了光学超振荡现象.理论研究表明,相位控制对于超振荡函数的构建至关重要[33].类似地,下面将看到在超振荡光场形成的过程中,光场相位分布起着十分重要的作用[34].空间光场分布E(r)可以由实振幅分布A(r)和相位分布φ(r)描述,即E(r)=A(r)exp[iφ(r)].由电磁场亥姆霍兹波动方程可知,光场振幅A(r)和相位φ(r)应满足

其中相位梯度∇φ(r)为光场的局域波矢量,即光场的局域空间频率.由(2)式的第2式可知,当局域空间频率大于波矢量绝对值k=2πn0/λ(即传播波的空间截止频率,n0为传播介质的折射率,λ为真空中的波长)时,光场振幅A(r)会在该局部空间产生衰减.特别是当|∇φ(r)|≫k时,将导致局域空间光场急剧衰减至零,进而形成超分辨光场结构.

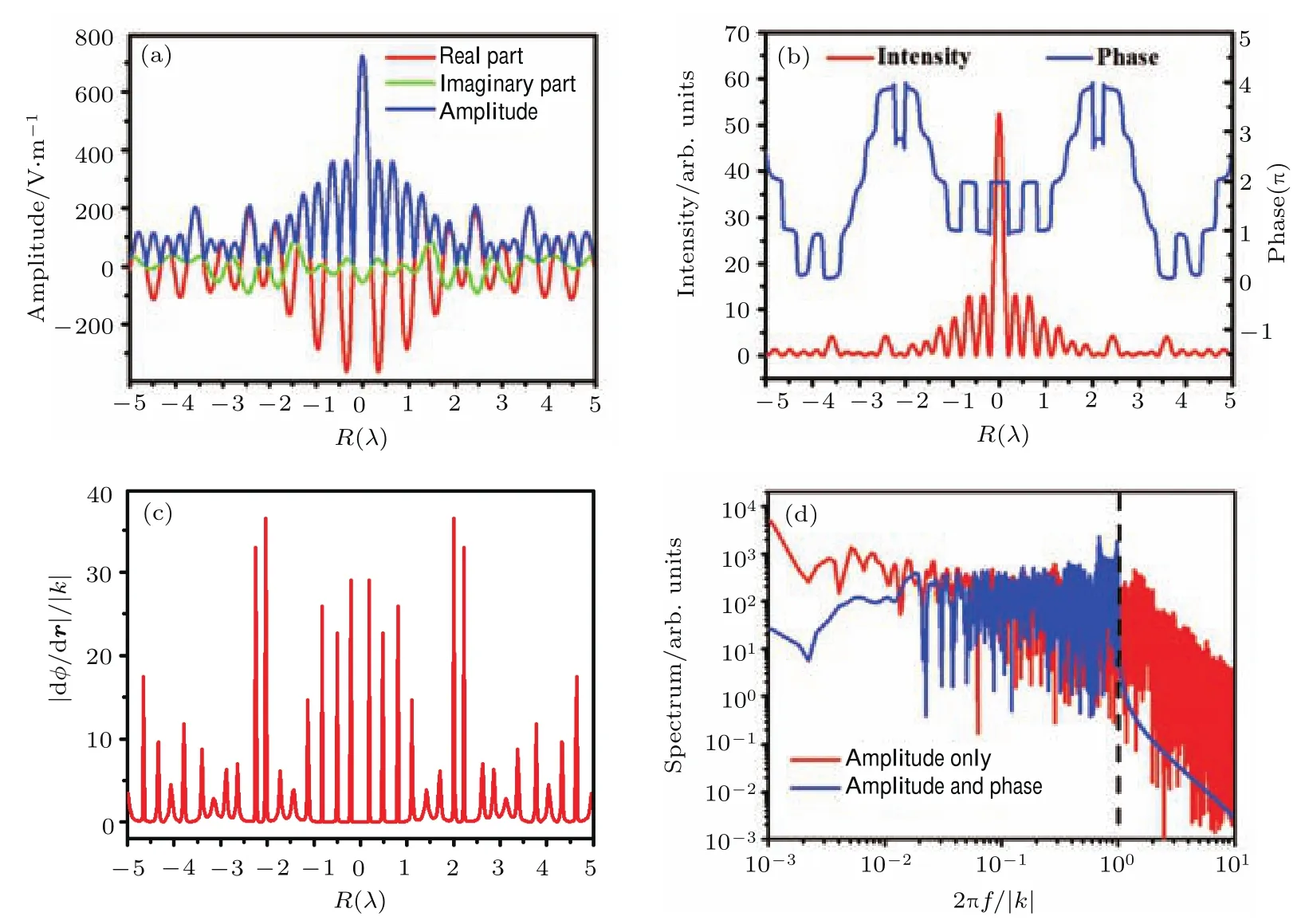
图2 超振荡聚焦光场示例[34](a)超振荡聚焦光场振幅(蓝)、光场实部(红)、光场虚部(绿)空间分布;(b)超振荡聚焦光场强度(红)、相位(蓝)空间分布;(c)超振荡聚焦光场的局域空间频率分布;(d)超振荡聚焦光场振幅的空间频谱(红)、超振荡聚焦光场(蓝)的空间频谱Fig.2.An example of super-oscillation focusing field[34]：(a)The amplitude(blue),real part(red)and imaginary part(green)of the optical super-oscillation focusing field;(b)the optical intensity(red)and phase(blue) distribution of the optical super-oscillation focusing field;(c)the local spatial frequency distribution of the optical super-oscillation focusing field;(d)the spatial frequency spectrum of the field amplitude(red)and full optical field (blue)of the optical super-oscillation focusing field.

图2给出了一维超振荡聚焦光场示例,其对应的聚焦光斑半高全宽为0.34λ(小于衍射极限0.5λ/NA).图2(a)为光场振幅(蓝)、光场实部(红)和光场虚部(绿)的空间分布;图2(b)给出了光场强度(红)和相位(蓝)的空间分布.可以看出,相位分布在光强度极小位置均出现了不同程度的反相跳变,尤其是在邻近主瓣的两个光强极小位置;如图2(c)所示,这种相位跳变导致该处局域空间频率|dφ(r)/dr|远远大于光传播空间截止频率k,致使该处振幅迅速衰减,形成半高全宽小于衍射极限的聚焦光场;图2(d)同时给出了光场振幅A(r)的空间频谱(红)和光场E(r)=A(r)exp[iφ(r)]的空间频谱(蓝).可以看出,光场振幅的空间频谱已经远远超出了传播波所对应的空间截止频率(黑色虚线).然而,相位的引入使得光场的空间频谱仅存在于小于空间截止频率的范围以内.事实上,从图2(a)可以看出,正是由于相位的反相跳变,使得光场实部和虚部的空间振荡频率均远低于振幅的空间振荡频率.因此,相位反相跳变在导致超分辨光场结构形成的同时,确保了整体光场空间频率小于传播波的空间截止频率,即在传播波中实现超分辨光场结构.通常,将光场局域空间频率|∇φ(r)|远大于光学系统空间截止频率kmax作为超振荡光场的特征[35,36].2014年,新加坡国立大学仇成伟等[37]提出了与瑞利判据(0.6λ/NA)相对应的超振荡判据(0.38λ/NA).

除了空间超振荡光场,近年来超振荡思想也被引入到时域光场,以实现时域脉冲压缩[38]、时域超分辨光拍[39],研究表明具有相同时间频率的超振荡时域光场和传统时域光场在损耗介质中的传播规律存在着较大的差异[40].

3 超振荡光场构建与超振荡光学器件设计方法

图3给出了超振荡聚焦光场分布主要参数[22]：焦斑强度、焦斑宽度、边带强度、视场、旁瓣强度.与传统的定义方式一致,焦斑强度是指中心亮斑的峰值强度I0,焦斑宽度通常用中心亮斑的半高全宽(FWHM)表示.与传统聚焦光场不同的是,这里引入了边带强度这一参数,用于描述超振荡光场中可能出现的巨大旁瓣,边带强度ISB通常远大于中心亮斑强度I0.视场是指边带所处位置以内的区域[-D,D].旁瓣强度是指在视场范围[-D,D]内最大旁瓣对应的强度ISL.

图3 超振荡聚焦光场的主要参数(为方便描述,并使全文术语一致,我们对原图进行了一定的改动)[22]：焦斑强度、焦斑宽度、边带强度、视场、旁瓣强度Fig.3.The major parameters for a super-oscillatory focusing field(the original fi gure is modi fi ed for consistent description in the whole paper)[22]：hotspot intensity,hotspot width,sideband intensity, field of view,and sidelobe intensity.

在超分辨器件设计方法研究方面,最早基于标量衍射理论,对超分辨光瞳滤波器进行了研究[41,42].罗切斯特大学Sales和Morris[43]以及清华大学Liu等[44]先后对超分辨光瞳滤波器的斯特列尔比(Strehl Ratio)、主瓣尺寸和旁瓣之间的相互制约关系进行了深入的理论研究,并给出了相应的光瞳滤波器设计方法,但其没有明显包含超振荡聚焦光场特有的边带强度和视场两个参数.2008年, Jabbour和Kuebler发展了一种基于粒子群优化算法的二值相位衍射器件设计方法,结合非旁轴衍射积分[45],实现了超分辨轴向聚焦点扩散函数的优化设计[46].2009年,Zheludev研究团队[47]提出了基于有限带宽函数的超振荡光场构建方法.根据光学器件的空间截止频率,在给定的局域空间(视场区域[-D,D])内,利用正交椭圆球面函数集的带宽有限特性和局域展开特性,可以构建任意尺寸的超分辨光场结构,并采用逆衍射方法求解光学器件的透射函数.然而,由于正交椭圆球面波函数的局域展开特性,所构建的超振荡光场在视场区域外存在巨大的旁瓣.值得关注的是,与传统的正透镜截然相反,利用该方法设计的聚焦透镜相位分布具有负透镜特征.由此可以看出超振荡透镜与传统透镜之间可能存在较大的区别,其设计方法不能够完全基于对传统成像或聚焦光学器件的认知. 2009年,浙江大学刘旭研究团队[48]提出了基于纳米光纤阵列多光束干涉的超振荡光场产生方法,并进行了理论仿真验证.2010年,多伦多大学Wong等[49]提出了基于超方向性天线阵列电磁场调控的超振荡聚焦场设计方法.2011年,英国圣安德鲁斯大学Mazilu研究团队[50,51],提出了一种基于光学本征模的超振荡光场构建方法.采用一系列光场分布尝试函数,在给定区域内构建强度算子和光斑尺寸算子.光斑尺寸算子最小本征值对应的本征模,决定了在该区域内能够实现的光斑最小尺寸. 2012年,Zheludev研究团队[18]提出了一种结合矢量光场衍射计算方法和粒子群优化算法[52]的超振荡光场构建与超振荡光学器件透射函数设计方法.根据超振荡光场分布目标函数,通过多次迭代,寻求超振荡光场和器件透射函数的最佳解.对于尺寸较大、结构参数复杂的器件,采用基因算法[53]和结合基因算法的粒子群算法[54],更有利于提高对全局最优参数的搜索能力.2013年,以色列理工学院和普林斯顿大学Green field等[55]提出了基于贝塞尔光束相干叠加的非衍射超振荡光束构建方法.通过不同阶次贝塞尔函数的线性叠加,可以获得任意小的光场结构.而且,由于贝塞尔光束的非衍射特性,所构建的超振荡光场结构可以在远距离传播过程中保持不变.但其不足之处是,在所构建的超振荡光场结构附近存在巨大的边带.2014年,仇成伟等[37]提出了基于衍射光场相干叠加的超振荡聚焦光场构建方法,对一组振幅、相位待定的同心环结构,将每个同心环结构的远场衍射光场进行线性相干叠加,并根据所构建的超振荡光场零点位置,通过求解非线性方程组,获取超振荡聚焦透镜的振幅、相位分布.然而,该方法无法避免超振荡聚焦光场中边带的产生.2014年,我们通过数值理论仿真研究发现,在焦斑半高宽约为0.31λ的超振荡聚焦情况下,仍然可以避免边带的产生,进而实现较大的视场[34].2015年,加拿大多伦多大学Wong和Eleftheriades[56]针对超振荡聚焦光场的边带问题,基于选择性超振荡的概念和超向天线设计方法,进一步从理论上验证了无边带的超衍射聚焦.同年,德国马普所Chremmos和Fikioris[57]将超振荡概念从传播波推广到倏逝波,利用平面介质界面处倏逝波的叠加,实现超振荡类型的近场光场,其振荡最小间隔小于最高衰减系数的倒数.2015年,美国代顿大学Zhan团队[58]利用径向偏振光聚焦光场的纵向偏振特性,将轴向光场振动等效于电偶极子振荡,通过计算电偶极子电场辐射传播,求解所需光瞳平面的光场分布,进而在4Pi聚焦系统中实现超振荡光针.2016年,以色列特拉维夫大学Eliezer和Bahabad[59]借鉴Berry和Popescu所给出的超振荡复函数[29],提出了一种基于艾里函数线性叠加的超振荡函数构建方法,并在空间频域实现了二维超振荡光场的空间频谱构建.

目前报道的大多数超振荡光场构建方法,只能在二维空间平面内实现光学超振荡.特别是当聚焦光场为单色光时,由于单一长度的波矢量无法支撑三维波矢空间,因此难以在三维空间的任意方向上实现光学超振荡.针对此问题,2017年多伦多大学Wong和Eleftheriades[60]提出了宽带超振荡的概念,利用具有一定时频带宽的宽带光源,在三维波矢空间形成一个实心球形状的波矢分布.对于给定的时间点,利用具有不同径向空间频率的球贝塞尔函数,构建具有球对称性的三维空间超振荡聚焦光场.然而,由于其时频宽带特性,这种三维空间光场分布会随时间演化,其三维超振荡光场分布只在布洛赫周期内较短的时间段内出现.

在以上超振荡光场和超振荡器件设计方法中,采用解析求解方法具有物理图像清晰的优点.然而,现有解析求解方法难以应用于复杂超振荡矢量光场的构建,而且不易实现光场和器件的最优化设计.因此,目前最常用方法仍是基于矢量光场衍射计算和粒子群算法、基因算法等的最优化设计方法,其最大优点是可以通过合理地设计适应度函数,进行多参数优化,实现复杂超振荡矢量光场的构建[34,61].同时,由上述分析可知,超振荡聚焦、成像器件的透射函数振幅相位特性以及其聚焦成像机理,可能完全有别于传统光学聚焦、成像器件.对于超振荡光场构建与超振荡光学器件设计,目前尚无系统的理论.特别是对于如何实现深亚波长聚焦、不随时间变化的三维超振荡聚焦、并有效地抑制边带、提高器件效率等,尚需对光学超振荡理论和超振荡光学器件设计的理论和方法开展深入研究.

4 矢量光场衍射计算方法

超振荡光场中的超分辨结构是相干光场精确干涉的结果.因此,如何准确地计算衍射光场分布是超振荡光场构建和超振荡光学器件设计的关键.在光的传播过程中,具有不同偏振特性的光场,其衍射规律也具有较大差别.特别是当考虑光场偏振(线偏振、圆偏振、径向偏振、角向偏振)、轨道角动量等时,其对应的衍射计算公式以及聚焦光场的偏振特性和强度分布等都存在巨大的差异.常用的光场衍射计算方法包括矢量角谱衍射方法[62,63]、瑞利-索末菲矢量衍射积分[64]和德拜-沃耳夫矢量衍射积分等[65].尽管采用这些计算方法所得到的衍射场分布存在一定差异,然而在大多数情况下均在可以接受的范围内[66].(3)式,(4)式和(5)式分别给出了在入射光强分布满足圆对称的条件下,线偏振光、圆偏振光、径向偏振光和角向偏振光[53,67-70]在空间柱坐标系(r,φ,z)和空间频率极坐标系(ρ, Φ)中对应的矢量角谱衍射计算公式：

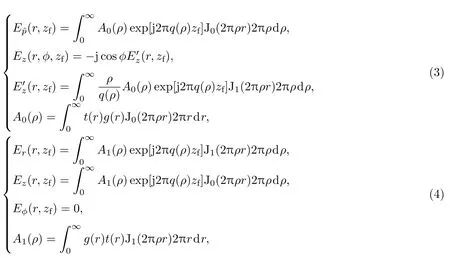
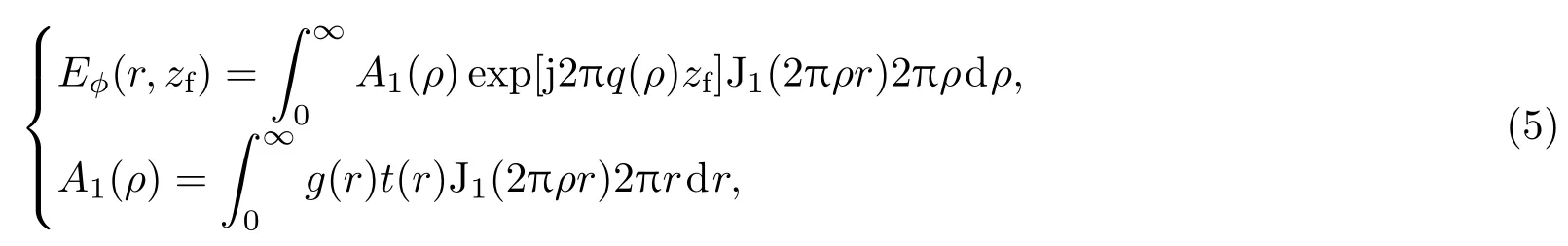
其中Eˆp,Eφ,Er和Ez分别为线(圆)偏振电场、角向偏振电场、径向偏振电场和轴向(纵向)偏振电场;g(r)和t(r)分别为入射电场的空间分布和器件透射函数;zf为光场衍射传播距离;J0和J1分别为零阶和一阶Bessel函数;q(ρ)=(1/λ2-ρ2)1/2为波矢量的轴向分量.相对于有限时域差分法[71]和有限元法等[72],(3)式、(4)式和(5)式所给出的衍射积分均可以通过快速汉克尔变换完成[73-75],从而实现矢量光场衍射的快速计算,有利于大面积、结构复杂、参数众多的超振荡光场和超振荡光学器件设计.当然,这些方法与严格求解麦克斯韦方程相比,仍有一定的差异[76].而且,这些衍射积分公式中并未包含器件亚波长结构散射、亚波长结构间光学耦合等因素,因此,可能造成理论设计和器件实际性能之间产生较大的差异.特别是在深亚波长分辨率器件的设计中,必须充分考虑这些因素的影响.对于结构简单、参数较少的超振荡器件,也可以采用模拟仿真软件,严格求解麦克斯韦方程,结合先验知识,通过不断调整参数的方式,在一定程度上实现超振荡器件的优化设计.

5 光场调控方法

研究发现,在亚波长尺度提高对光场振幅、相位、偏振的调控范围和调控自由度,可以极大地改善超振荡聚焦/成像器件的光能利用效率和空间分辨率,并有效地抑制旁瓣[34].特别是在产生具有特殊电场/磁场分布的超振荡光场时,对光场的精确调控显得尤为重要.超表面结构[77]可以实现对光场振幅、相位、偏振以及角动量等参数的调控,其单元尺寸通常小于波长,为实现亚波长尺度下光场的高效调控提供了重要的途径.

在可见光到红外光波段,超表面结构已有大量报道.2003年,斯坦福大学Crozier等[78]发现金属条阵列结构在光学波段具有类似于天线的作用. 2011年,哈佛大学Capasso研究团队[79]提出了一种“V”形光学天线,对波长为8µm的红外光波,其相位调控范围达到了2π,但振幅透射率小于10%. 2013年,美国哥伦比亚大学Li和Yu[80]提出通过电调谐石墨烯的光电导率改变石墨烯-金属等离激元天线谐振,实现红外光波的振幅相位调控.理论仿真表明：对波长为7.05µm的光场,其相位调控范围达到了240°,振幅调控范围为0—0.9,但其无法对相位和振幅进行独立调控.2013年,南丹麦大学Bozhevolnyi等[81]提出了一种金属条形天线结合金属反射层的高反射率光场相位调控结构,对波长为800 nm的光场,其相位调控范围达到2π,光强反射率约为40%.2014年,以色列特拉维夫大学Yifat等[82]提出了一种基于偶极子-片状天线结构的反射天线阵列,对波长为1550 nm的光场,相位调控范围达到了300°,振幅调控范围为0.79—0.95. 2015年,加州理工学院Arbabi等[83]针对1550 nm波长,采用亚波长介质圆柱阵列,通过改变圆柱直径和周期,实现了对透射光场的相位调控,其相位调控范围达到了2π.2016年,Capasso研究团队[84]提出了一种长方形介质柱结构,利用几何相位,通过结构旋转实现了2π的相位调控范围.在偏振调控方面,采用透射型同心圆金属光栅[85],可以将圆偏振光束转化成为径向偏振光束.2014年,美国滨州州立大学Mayer研究团队[86]提出了一种宽带(640—1290 nm)、宽视场的反射型超表面结构波片,基于强耦合的纳米棒谐振器阵列,实现了四分之一和半波片功能,转换效率达到了92%以上.同年,南京大学和美国西北大学共同提出了一种无色散的“L”形双折射偏振调控超表面结构[87].2016年,美国代顿大学Wang和Zhan[88]对波长为1064 nm的圆偏振入射光,提出了一种具有高反射率的“T”形双折射结构.通过旋转该结构可以控制出射光偏振方向,并通过改变结构参数可实现二值相位(0, π)调控.在轨道角动量调控方面,采用叉型全息光栅[89,90]可以实现任意轨道角动量的控制.然而,由于采用全息产生方式,其出射光束与入射光束不同轴,在应用上比较受限.2016年,罗先刚研究团队分别提出了一种悬链线超表面结构[91]和一种结合几何相位和等离子相位延迟的相位调控方法[92],可以实现对光场轨道角动量的任意调控.2016年, Capasso研究团队[93]报道了一种结合叉型全息光栅结构和结合环形光栅结构集成化涡旋光束波片,实现了轨道角动量产生功能和径向偏振光束产生功能的集成化.

通常,反射型超表面结构具有较高的效率,而透射型超表面结构则效率较低.然而,反射结构在很多实际应用中受到较大的限制.虽然采用多层结构可以在一定程度上提高透射型超表面结构的效率,但是这将极大地增加其制作难度和成本.而且,现有超表面结构的功能比较单一,这些都极大地限制了超振荡光学器件的发展.如何有效地提高透射型超表面结构效率、实现光场的多参量(振幅、相位、偏振等)同时调控,并提高各参量的调控范围,亟待开展深入研究.

6 超振荡聚焦与超振荡光学器件

近年来,光学超振荡光场产生和超振荡光学器件的研究得到了快速发展.已报道的超振荡光学器件以单波长超振荡光学聚焦器件为主.早期的器件主要是基于简单二值振幅调控实现相干光场的远场超分辨聚焦,其焦斑尺寸可小于1/3倍波长,然而旁瓣巨大;采用连续振幅调控方式,可以在一定程度上抑制旁瓣,提高器件的效率,并在实现光学超振荡的同时,将旁瓣比(最大旁瓣强度与主瓣强度之比值)压缩到12%以下;采用相位调控,通过相干相消和相干相长,对主瓣半宽进行压缩,有利于进一步大幅提高器件聚焦效率、抑制旁瓣.理论上,在相位调控中,采用的相位值越多,越有利于提高器件的性能.然而,在光学波段,由于加工条件受限,实现较大面积的多值相位调控,具有较大的困难.采用二值相位(0,π),不但能够提高器件性能[34,94,95],而且便于加工制作.以下我们对近年来报道的超振荡聚焦器件及其性能进行详细的介绍.

6.1 超振荡线聚焦光场及器件2009年,Zheludev研究团队[47]基于正交椭圆球面函数和标量衍射理论,设计了一种超振荡光学聚焦透镜,数值计算表明这种透镜具有超分辨成像功能,理论上可实现任意小的空间分辨率.与传统的聚焦透镜不同,这种透镜的振幅透射率在中心位置附近呈现振荡衰减,而其相位分布类似于凹透镜,并在透射率为零位置出现相位(约为π)跳变.

图4 基于亚波长金属狭缝阵列的准连续振幅调控超振荡线聚焦器件[100](a)器件结构示意图,其中金属材料为铝,基底为蓝宝石玻璃,T为狭缝周期,Wi为第i个狭缝的宽度;(b)聚焦器件的扫描电镜照片;(c)采用纳米探针获得的二维聚焦光场强度分布;(d)聚焦光场强度分布曲线Fig.4.The quasi-continuous amplitude modulation super-oscillatory focusing device based on sub-wavelength metal slit array[100]：(a)The device structure,where the metal is aluminum,the substrate is sapphire glass,T is the period,and Wiis the width of the i-th slit;(b)the SEM picture of the device;(c)the 2-D intensity distribution of the focusing optical field obtained with a nano-tip;(d)the intensity curve of the focusing optical field.

在透镜焦平面上,所设计的视场[-D,D]之外伴随有巨大的边带.该透镜加工难度极大,尚未见实验报道.2011年,Wong和Eleftheriades[96]通过控制多根天线所发射电磁场的振幅和相位,在毫米波段实验演示了远场亚波长聚焦,焦距达到5λ,焦斑半高全宽为0.45λ(0.74倍衍射极限).2014年,重庆大学研究团队[97]报道了基于准连续振幅调控和二值相位调控的双层金属缝超振荡聚焦透镜的理论设计.利用金属光波导直径与等效折射率之间的关系,通过调整每层金属光波导的直径,分别对双层金属缝的等效折射率实部和虚部进行调控,进而实现对出射光振幅和相位的控制.理论仿真表明,该透镜焦距为20λ,焦斑半高全宽为0.32λ(0.64倍衍射极限).同年,美国犹他大学Wan等[98]基于标量衍射理论和非线性优化方法,针对400 nm波长设计了一种基于二值相位调控的超衍射透镜,焦距100λ,半径143.5λ,焦斑半高宽为196 nm(0.80倍衍射极限).美国大学Maklizi等[99]提出了一种基于金属双狭缝和金属光栅阵列的线聚焦透镜.金属狭缝用于激发表面等离激元,光栅阵列用于对表面等离激元进行散射和散射光的相位调控,进而实现可见和紫外横磁波(TM)线偏振光的超振荡聚焦.通过调整金属双狭缝的间隔等参数,可以对光栅间的相位差进行优化,以实现对焦斑尺寸的压缩.理论仿真表明,其焦斑半高全宽约为λ/4.2016年,重庆大学研究团队,对横电波(TE)线偏振光,采用单层亚波长金属狭缝,通过改变狭缝宽度,实现了对光场振幅(0—1)的连续调控,并报道了一种基于振幅连续调控的远场超振荡线聚焦透镜,图4给出了该透镜的结构及超振荡聚焦实验结果.实验表明,该透镜焦距为40.1λ,焦线半高全宽为0.379λ(0.75倍衍射极限),而旁瓣比仅为10.6%.在突破超振荡判据(0.38λ/NA)的条件下,较好地解决了旁瓣的抑制问题[100].同年,该研究团队报道了一种基于二值振幅和二值相位调控的远场超振荡线聚焦透镜.通过金属膜和介质厚度,分别控制出射光的振幅(0,1)和相位(0,π).透镜焦距达到148λ,焦线半高全宽为0.406λ(0.76倍衍射极限),旁瓣比为22%[101].2016年,Zheludev研究团队[102]利用二值振幅型金属狭缝阵列线聚焦超振荡透镜,在实验上演示了单光子量子超振荡行为.

6.2 超振荡点聚焦光场及器件

2006年,麻省理工学院Stanley等[103]基于平面波角谱理论,采用非聚焦波前相干叠加,实现了0.37λ的亚波长分辨率聚焦.2010年,中国科学院光电技术研究所等单位[104]提出了一种基于表面等离激元散射波的远场超分辨聚焦透镜,该透镜由亚波长环形狭缝和环形光栅构成.径向偏振入射光通过狭缝激发表面等离激元,环形光栅对表面等离激元散射产生的光波与透过环形狭缝的光波,在远场干涉形成光斑.理论仿真表明,当焦距为0.57λ时,焦斑半高全宽可达到0.40λ.该方法被进一步推广到双波长超分辨聚焦透镜设计中[105],并在实验上获得了半高全宽为0.41λ的焦斑.2011年,美国马里兰大学Liu等[106]在单模光纤端面直接制作同心环结构的表面等离激元透镜,利用表面等离激元只能被TM波激发的特性,产生径向偏振出射光场.并利用TM模式在不同宽度狭缝中传播的色散特性,结合平面透镜相位空间分布,实现了对出射径向偏振光场的超分辨聚焦,其焦斑半高全宽达到了0.55λ(0.62倍衍射极限).2012年,Zheludev研究团队[18]报道了一种二值振幅型的金属铝同心环结构超振荡透镜,工作波长为λ=640 nm.实验表明：该透镜焦距为10.3µm,焦斑半高全宽为0.29λ(0.52倍衍射极限),但旁瓣较大、且紧靠中心焦斑.2013年,该研究团队采用“十”字金属孔阵列实现类似于传统聚焦透镜的相位分布,对波长为800 nm的入射光实现了超振荡聚焦.实验表明：透镜焦距为14.7λ,焦斑半高全宽达到了0.28λ[107]. 2014年,新加坡国立大学等单位[37]共同报道了一种基于二值振幅和二值相位调控的同心环结构超振荡聚焦透镜的理论设计,焦斑半高全宽达到了0.34λ.然而,在其焦斑中心15λ距离外存在巨大的边带旁瓣.2015年,西安交通大学刘涛等[108]报道了基于二值同心环结构的超振荡透镜理论设计,并实验报道了一种基于二值振幅的线偏振光超振荡透镜,其工作波长为532.4 nm,焦距为60.7λ,焦斑半高全宽理论值为0.36λ,实验测得的焦斑半高全宽约为0.45λ(0.86倍衍射极限).同年,罗先刚研究团队[109]通过条形金属缝旋转所形成的几何相位,实现了对圆偏振光相位的连续调控,首次在实验上报道了一种超宽带(405—784 nm)超振荡聚焦透镜,透镜数值孔径为0.24,焦斑尺寸小于0.7倍衍射极限.然而,该透镜存在较大的色差.2016年,重庆大学研究团队[67]报道了一种基于二值振幅(0, 1)和二值相位(0,π)调控同心环结构点聚焦透镜.图5给出了该透镜的工作原理、基本结构、理论设计结果和实验测试结果.该透镜对圆偏振光实现了超振荡聚焦,焦距为399.5λ,焦斑半高全宽为0.454波长(0.71倍衍射极限),旁瓣比达到26%.在实现超振荡聚焦的同时,较好地抑制了旁瓣.同年,该研究团队报道了一种基于二值相位调控(0,π)的宽带亚波长聚焦透镜理论设计,其设计结果如图6所示,在630—680 nm波长范围内实现了超衍射亚波长聚焦,焦斑半高全宽小于288 nm(约0.86倍衍射极限)[110].然而,与之前报道的基于相位连续调控的超宽带超振荡聚焦透镜类似,这种基于二值相位的宽带聚焦透镜也存在严重的色差.针对平面透镜的色差问题,罗先刚研究团队[111]提出利用结构色散和材料色散补偿消除色差的方法,要求空间相位变化与波长的乘积在整个器件范围内为常数,从而实现宽带消色差平面光学器件.然而,这种对相位分布的特殊要求,目前尚难以应用于超振荡透镜设计.2017年,西北工业大学Li等[112]报道了一种基于二值振幅调控的多焦点超振荡透镜理论设计,对于线偏振光或圆偏振光,在轴向实现了多点聚焦,其焦斑尺寸约为λ/3.除了上述基于表面等离激元的超振荡透镜和基于波带片结构的超振荡透镜以外,2016年,新加坡国立大学洪明辉研究团队[113]报道了一种微球超振荡聚焦透镜.在微球透镜入射端中心设置挡光模板阻挡近轴光束,实现超振荡光学聚焦,并可以通过改变挡模板尺寸来改变工作距离和焦斑尺寸.实验表明,对633 nm波长的线偏振光,聚焦光斑半高全宽达到了0.387λ.该透镜的不足之处是工作距离较短,当焦斑尺寸小于衍射极限时,其工作距离小于λ.特别是当工作距离远小于波长时,其聚焦光场部分包含倏逝光场.

图5 圆偏振光超振荡聚焦器件[67](a)圆偏振光超振荡聚焦原理示意图;(b)同心圆环形聚焦器件结构示意图(图中只给出了圆环结构的一半视图和截面图),其中金属环(蓝)为金属铝、深灰色为Si3N4、浅灰色为蓝宝石玻璃基底;(c)超振荡光场理论设计结果：光场强度分布(上),光场的相位(红色)和振幅(紫色)分布(下),插图为局域空间频率分布;(d)圆偏振光超振荡聚焦器件的扫描电镜照片;(e)采用纳米探针获得的二维聚焦光场强度分布;(f)焦平面上光强度沿Y轴(上)和X轴(下)的分布Fig.5.Super-oscillatory focusing device for circularly polarized wave[67]：(a)The focusing of circularly polarized plane wave;(b)the structure of the lens,where metal ring(blue)is aluminum,the dialectical ring(deep gray)is Si3N4,and the substrate(light gray)is sapphire glass;(c)the theoretical design result of the super-oscillation focal spot：optical intensity distribution(top),the phase(red line)and amplitude(purple line)distribution(bottom),and the inset is the local spatial frequency;(d)the SEM picture of the device;(e)the 2-D focusing optical field intensity obtained with the nano-tip;(f)the optical intensity distribution along the Y-axis and X-axis on the focal plane.

相较于线偏振光和圆偏振光,对柱对称偏振(径向偏振、角向偏振)光束进行聚焦,有望获得更小的聚焦光斑[114,115].2013年,哈尔滨工业大学谭久彬研究团队[68]基于粒子群算法和矢量角谱衍射计算方法,报道了一种基于二值振幅同心环结构径向偏振光聚焦器件的理论设计,在空气中焦斑半高全宽达到0.389λ(0.728倍衍射极限).2015年,罗先刚研究团队[116]报道了一种基于等离激元的聚焦透镜,对角向和径向偏振光实现了超振荡聚焦.通过在透镜中心设置金属膜挡光圆盘,提高聚焦光场中的轴向偏振分量、降低径向偏振分量,进而减小焦斑的半高全宽.当遮挡率为0.7时,焦斑半高全宽降为0.47λ.2016年,重庆大学研究团队[69]报道了一种基于二值相位(0,π)调控的角向偏振超振荡聚焦透镜,在焦平面产生超振荡空心光环,器件的理论设计结果和实验测试结果如图7所示.实验表明：该透镜焦距为600λ,所产生的空心光环内径半高全宽为0.61λ(0.78倍衍射极限).2016年,俄罗斯科学院图像处理系统研究所Sta ff eev等[117]采用偏振转换器结合菲涅耳波带片,对角向偏振光和径向偏振光实现了亚波长聚焦,焦斑在两个正交方向的半高全宽分别为0.28λ和0.458λ.

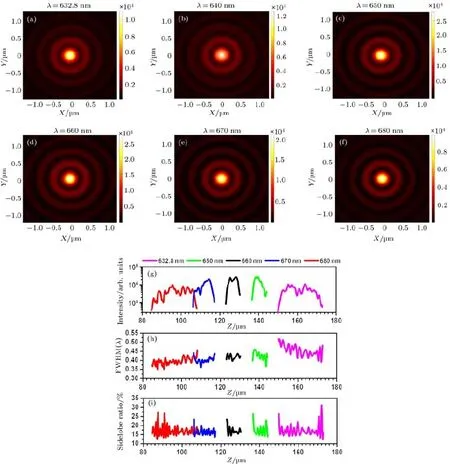
图6 宽带超振荡聚焦器件理论设计结果[110](a)—(f)分别为在632.8,640,650,660,670,680 nm波长照明下,在相应焦平面上的二维光强度分布;(g)—(i)分别为各波长聚焦焦斑峰值强度、半高全宽和旁瓣比(最大旁瓣强度与与主瓣强度之比)的轴向分布Fig.6.The theoretical design result of the broad-band super-oscillatory focusing device[110]：(a)–(f)The 2-D optical intensity distribution on the focal plane under illumination of di ff erent wavelengths of 632.8,640,650,660,670,680 nm; (g)–(i)the optical intensity and transverse FWHM and sidelobe ratio(the ratio of maximum sidelobe intensity to peak intensity)along the optical axis.

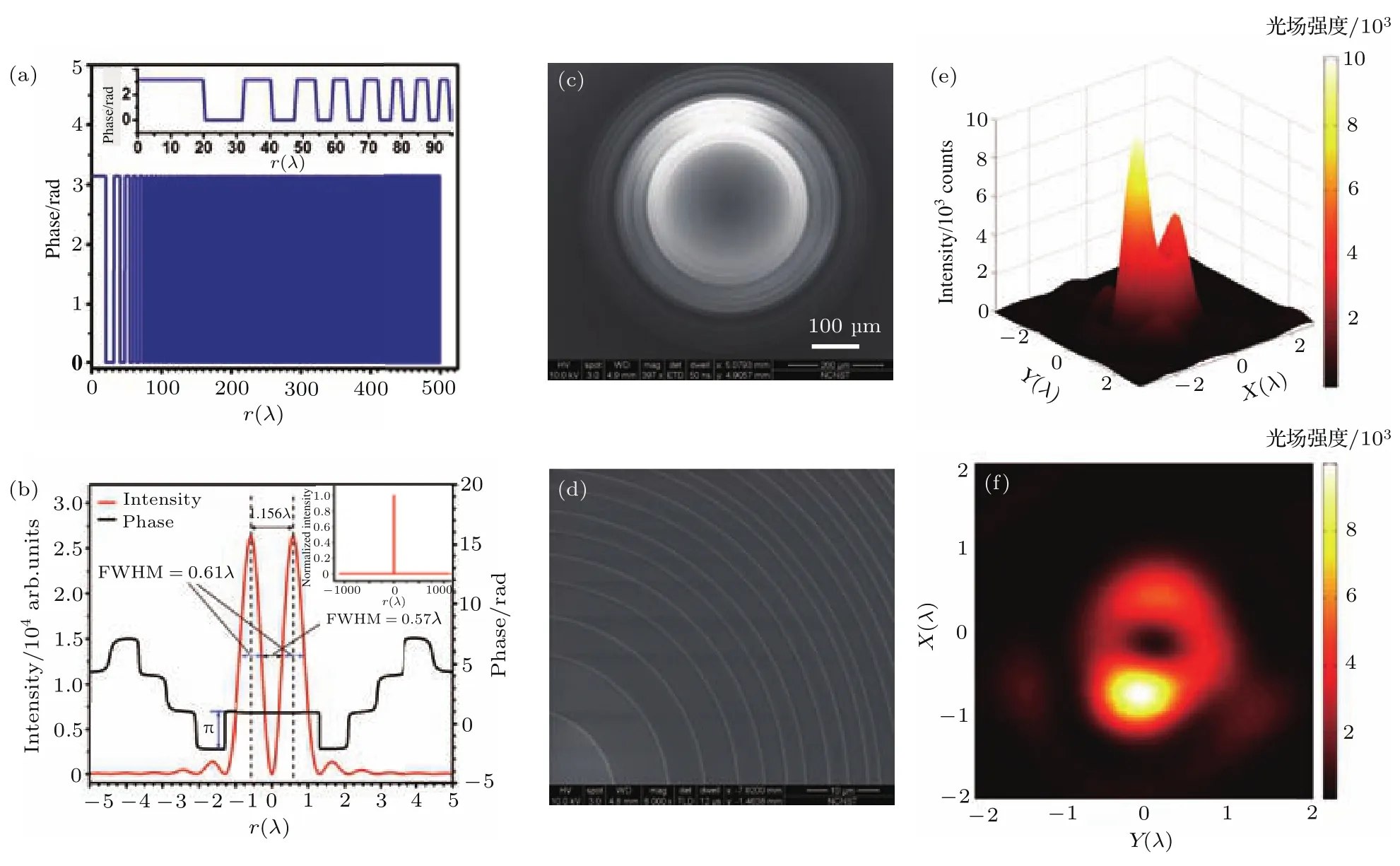
图7 角向偏振光聚焦器件及超振荡空心光场产生[69](a)角向偏振光聚焦器件的相位沿径向分布理论设计结果;(b)角向偏振光超振荡聚焦光场的强度(红)与相位(黑)沿径向分布理论设计结果;(c),(d)角向偏振光聚焦器件的电子显微镜照片;(e),(f)采用纳米探针获得的角向偏振二维聚焦光场强度分布Fig.7.The focusing device for azimuthally polarized wave and the generation of super-oscillatory hollow optical field[69]：(a)The phase distribution of the focusing device for azimuthally polarized wave along the radial direction;(b)the optical intensity(red)and phase(black)distribution of the azimuthally polarized super-oscillation hollow spot;(c),(d)the SEM picture of the focusing device;(e),(f)The 2-D focusing optical field intensity obtained with a nano-tip.

2015年,以色列理工学院David等[118]报道了一种基于金属-氧化物-硅平面结构的聚焦器件,采用波长为671 nm的圆偏振光,通过狭缝激发波长为184 nm的短波长波导模式,并利用阿基米德曲线光栅,在器件表面近场区域形成超分辨聚焦光场,实现了半高全宽约67 nm的焦斑;并通过激发两种短波长(200和282 nm)波导模式,利用两者的相干叠加,在器件表面近场区域形成了半高全宽约35 nm的光场结构(非焦斑).尽管聚焦光场中出现了类似于光学超振荡现象中的相位反相跳变现象,然而其聚焦光场的二维傅里叶空间频谱分布范围已经远超出了波导模式所对应传播波的空间截止频率.因此,该超分辨光场主要还是光波导表面的倏逝光场,而非严格意义上的超振荡聚焦光场.

6.3 特殊超振荡光场及器件

2008年,新加坡数据存储研究所Wang等[119]提出了一种超振荡纵向偏振光场的产生方法.采用高数值孔径透镜增强聚焦光场中的纵向偏振分量,并对由5个同心圆环构成的二值相位偏振滤波器进行优化设计,在聚焦光场中进一步滤除径向偏振分量,并实现强度沿轴向均匀分布的纵向偏振聚焦光场.理论仿真表明,该聚焦光斑横向半高全宽为0.43λ,轴向长度为4λ.2013年,新加坡国立大学等单位[120]基于矢量索末菲-瑞利衍射积分公式和粒子群算法,对波长为632.8 nm的径向偏振入射光,理论设计了一种二值振幅同心环结构的超振荡透镜,以产生纵向偏振聚焦光场,焦斑半高宽为0.39λ,并较好地抑制了旁瓣,其旁瓣比约为25%. 2013年,Zheludev研究团队[121]在二值振幅型同心环超振荡点聚焦器件中心位置增加金属膜挡光圆盘,从而在聚焦区域形成阴影区,降低了焦平面旁瓣强度,并利用泊松亮斑效应实现长焦深聚焦.实验表明,对波长为640 nm的线偏振光,该器件在光轴上4—10µm范围内均能实现聚焦,焦斑半高全宽小于0.42λ,焦深达到10λ.与前述的纵向偏振聚焦光场不同,该聚焦光场主要为焦平面内的线偏振分量.2014年,新加坡南洋理工大学与英国南安普顿大学[122],共同报道了一种长焦深超分辨聚焦透镜,采用二值粒子群算法和瑞利-索末菲矢量衍射积分公式,利用超高斯函数描述光针的纵向分布,并将其作为聚焦光场目标函数对器件进行最优化设计.实验表明,对波长为405 nm的圆偏振光,该器件焦距为7µm,焦深为15λ,焦斑半高全宽小于0.45λ.罗先刚团队[123]报道了一种基于表面等离激元散射的长焦深超分辨聚焦透镜,该透镜由一个环形金属狭缝和多个同心环金属光栅构成,由垂直入射的径向偏振光通过金属狭缝激发表面等离激元,由于同心环金属光栅的散射和相位调制作用,散射光在远场相干叠加形成聚焦光斑.通过改变光栅刻槽深度可以实现对焦斑尺寸、焦深和焦距的控制,焦深可达2.7λ,对应的焦斑半高全宽约为0.44λ.文献[124]报道了一种超长超振荡光针的产生方法及其数值仿真结果.采用顶角为90°的锥反射镜,对径向偏振光进行聚焦.利用45°的内锥面反射,将径向偏振完全转化成为轴向偏振光束,同时最大限度地利用了波矢量在焦平面内的分量,在锥反射镜光轴上产生了半高全宽为0.36λ、长度为50000λ的超振荡轴向偏振光针.2015年,新加坡国立大学和中国科学院光电技术研究所[125]共同报道了一种基于二值相位调控的长焦深聚焦透镜,对波长为633 nm、轨道角动量为1的角向偏振光进行聚焦.为了产生超长焦深,该透镜采用了中心金属膜挡光圆盘.实验表明：该透镜焦距为240λ,焦深约为12λ,焦斑半高全宽为0.42λ—0.49λ.采用带轨道角动量的角向偏振光聚焦的最大优点在于可以避免介质界面对光传播的影响.2016年,西安交通大学刘涛等[126]针对线偏振光和圆偏振光,对基于二值振幅调控的同心金属环平面器件进行优化设计,以产生具有横向偏振的超衍射聚焦光针.仿真结果表明：光针长度为12.4λ,其横向半高全宽约为0.31λ—0.67λ.同年,重庆大学研究团队[70]报道了一种基于二值相位同心环的超振荡聚焦透镜,图8给出了该器件的理论设计结果与实验测试结果.对632.8 nm的径向偏振光实现了超振荡聚焦,焦距为200λ.在实验上获得了纵向偏振超振荡聚焦光场,焦斑横向半高全宽为0.456λ,焦深达到5λ. 2017年,哈尔滨工业大学谭久彬研究团队[127]对轨道角动量为1的角向偏振光束采用二值相位板和高数值孔径物镜实现超分辨聚焦,理论仿真表明：实现了轴向长度为6λ的横向偏振光针,其横向半高全宽为0.40λ—0.48λ.同年,重庆大学研究团队设计了一种角向偏振超振荡空心光针产生器件(Planar Bianry-phase Lens for Super-oscillatory Optical Hollow Needles，Scienti fi c Reports,已录用).针对角向偏振光,基于粒子群算法和矢量角谱衍射公式,在设计中要求沿光轴300λ—310λ范围内的聚焦空心环半高宽小于0.4λ.通过该器件实验产生的空心光针长度大于10λ,空心光针内径半高全宽为0.34λ—0.52λ(0.62—0.94倍衍射极限).仿真表明该空心光针在空气-水界面具有优异的穿透性,而且在水中其长度几乎增加了一倍.在超长超振荡光针的设计中,通过空间频谱压缩,可以实现长度达80λ以上的超振荡空心光针.类似地,该空心光针在水中的长度可以达到160λ以上.这种超长超振荡空心光针有利于提高受激辐射淬灭显微技术(STED)横向分辨率和探测深度[128].

图8 径向偏振光聚焦器件及纵向聚焦光场的产生[70](a)焦平面光场的径向分量的强度(红)、相位(蓝)和纵向分量的强度(黄)、相位(紫)沿径向分布的理论设计结果;(b)聚焦光场的峰值强度(蓝)、横向半高全宽(紫)和旁瓣比(红)沿轴向分布的理论设计结果,其中黑色虚线和黄色虚线分别表示衍射极限(0.5λ/NA)和超振荡判据(0.38λ/NA);(c)径向偏振光聚焦器件的扫描镜照片;(d), (e)采用纳米探针获得的聚焦光场焦平面和传播平面的二维光场强度分布;(f)聚焦光场峰值强度(红)、焦斑横向半高全宽(蓝)的理论仿真结果(实线)与实验结果(空心)的比较Fig.8.The focusing device for radially polarized wave and the generation of longitudinally polarized focusing optical field[70]：(a)The theoretically designed optical intensity and phase distribution of the radially polarized component and longditudinally polarized component on the focal plane;(b)the theoretically designed peak optical intensity,transverse FWHM and sidelobe ratio along the optical axis;(c)the SEM picture of the device;(d),(e)the 2-D focusing optical field intensity on the focal plane and the propagation plane obtained with the nano-tip;(f)the comparison of peak optical intensity(red)and transverse FWHM(blue)between the theoretical(solid line)and experimental(open markers)results.

在非衍射超振荡光束的研究方面,2011年,以色列理工学院Makris和Psaltis[129]从理论上研究了具有亚波长结构的非衍射光束的传播特性.2013年,以色列理工学院Green field等[55]利用空间光调制器在实验上演示了具有亚波长结构的非衍射超振荡光场,其非衍射传播距离达到了250瑞利长度.2017年,重庆大学研究团队[130]实验报道了一种非衍射的超衍射光束产生方法.采用相位型空间光调制器,实现了一种焦距为1 m、数值孔径为0.005的超振荡聚焦反射镜.实验结果如图9所示,对波长为632.8 nm的线偏振光进行聚焦,所形成的焦斑横向半高全宽小于62µm(小于衍射极限0.5λ/NA)、轴向长度大于43.3 mm,焦斑的长宽比接近700.与点聚焦光束相比,该光束具有较窄的径向空间频率分布.然而,其光场相位空间分布具有明显的超振荡特征：在主瓣零点位置出现π相位跳变,且在该位置光场局域空间频率大于该器件数值孔径所对应的空间截止频率.通过增大数值孔径有望进一步缩小该非衍射光束的横向尺寸.同年,Eliezer和Bahabad[59]采用Lee[131]的方法将基于艾里函数构建的二维超振荡函数频谱转化为纯相位空间分布,通过相位型空间光调制器实现二维超振荡光场频谱,并通过二维傅里叶变换透镜实现二维超振荡光场.由于采用艾里光束构建,在传播中存在障碍物时,该超振荡光场可以通过来自于邻近光场的能流实现自我恢复.

从已有报道的超振荡光场和超振荡聚焦器件可以看出,其主要是实现了二维平面内的空间超分辨,而空间分辨率多在λ/3左右.尽管大多数报道并没有提及效率问题,然而效率较低是目前超振荡器件面临的一个不可回避的问题.如何进一步实现三维深亚波长聚焦、提高器件的效率,将是今后超振荡器件的研究重点和难点.对于超振荡光学器件的制备,在可见光及近红外光波段,由于超振荡器件基本结构的特征尺寸较小,通常采用电子束曝光、聚焦离子束刻蚀等技术进行器件的制作.为降低加工精度要求,可在器件设计时将基本结构特征尺寸提高到微米量级,以便采用激光图形发生器进行加工.然而,这种以增大特征尺寸降低加工难度的方式,会在很大程度上降低器件的性能,特别是器件的聚焦效率.

7 超振荡光场表征技术

超振荡光场的测试方法主要包括接触式测试和非接触式测试两种.常用的接触式测试方法主要有纳米探针扫描法和刀口法,而非接触式测试方法主要采用光学显微法.以下我们将对常用的超振荡光场测试方法进行介绍与分析.

7.1 基于纳米探针扫描的超振荡光场表征技术

采用纳米光纤探针对超振荡光场进行逐点扫描,可获得超振荡光场强度的空间分布,其空间分辨率主要取决于探针尺寸,目前报道的最小分辨率可达30 nm[51].2007年,Zheludev研究团队[32]利用近场光学扫描显微镜探针,对纳米孔阵列的衍射光场(波长为660 nm)进行扫描,首次从实验上观测到了半高全宽为235 nm的超振荡光斑.2011年,该研究团队[51]采用直径为30 nm的纳米探针,获得了半高全宽为222 nm(0.45倍衍射极限)的光强分布.然而,带孔纳米探针具有较强的偏振选择性.相对于与探针端面垂直的电场偏振分量,探针对与其端面平行的电场分量具有更高的耦合效率[132].

图9 非衍射-超衍射光束的产生[130](a)XZ传播平面内的光场强度分布实验结果;(b)Y Z传播平面内的光场强度分布实验结果;(c)聚焦光场的峰值强度(红)、横向半高全宽(蓝)和旁瓣比(绿)的轴向分布,其中黑色虚线和褐色虚线分别表示衍射极限(0.5λ/NA)和超振荡判据(0.38λ/NA);(d)在焦距1000 mm处光场的相位分布(蓝)和局域空间频率分布(红),其中黑色虚线代表数值孔径NA=0.005所对应的最高空间频率Fig.9.The generation of non-di ff racting sub-di ff raction beam[130]：(a)The optical intensity distribution on the XZ propagation plane;(b)the optical intensity distribution on the Y Z propagation plane;(c)the peak optical intensity(red), transverse FWHM(blue)and sidelobe ratio(green)along the optical axis,where the black dashed line and the brawn dashed line represent the di ff raction limit and the super-oscillation criteria respectively;(d)the phase distribution(blue) and the local spatial frequency(red)distribution along the radial coordinate on the focal plane at Z=1000 mm,where the black dashed line denotes the highest spatial frequency corresponding to a numerical aperture of 0.005.

因此,在纵向偏振光场测试中,可采用弯曲探针进行扫描[70],这是纳米探针扫描法的优势之一.2016年,重庆大学研究团队采用弯曲纳米探针实现了线偏振[100,101]、圆偏振[67]、角向偏振[69]、纵向偏振[70]超衍射光场的测量.尽管采用弯曲探针可以在一定程度上提高纵向光场的检测灵敏度,然而其代价是削弱了对水平偏振分量的检测灵敏度.采用无孔径探针可以实现电场三个分量的测量[133],但其散射光场耦合难度较大.此外,通过在纳米探针顶部固定荧光单分子,利用荧光单分子偶极矩可以实现偏振选择性检测[134].总体而言,基于纳米探针扫描的超振荡光场表征技术的缺点是速度较慢,并且该方法对空间扫描分辨率、重复定位精度、探测器灵敏度都有很高的要求.

7.2 基于刀口法的超振荡光场表征技术

刀口法是一种常用的光场分布测试方法.采用边缘平整的刀口,对被检测光场进行局部阻挡,检测未被阻挡的光场能量,最后根据扫描结果,采用相应的重构算法求解被检测光场的强度分布.在超分辨光场分布的测量中,为了减小由于刀口边缘衍射效应引起的误差,通常将刀口直接制作在光电探测器表面,这样不但可以实现对传播光场的测量,而且还可以实现对非传播光场(如纵向偏振光场)的测量[135].2010年,日本京都大学Kitamura等[136]将刀口直接制作在探测器探测面上方,对波长为980 nm的纵向偏振焦斑进行测量,并根据多个方向的扫描结果,采用Radon逆变换[137]进行二维光强分布重建.在刀口粗糙度为30 nm的条件下,获得了半高全宽为0.4λ的焦斑光强分布.为了避免使用复杂的Radon逆变换,2013年,中山大学Xie小组[138]采用双刀口法进行超分辨光斑的测量,将直角硅片作为刀口安装在探测器上方,刀口粗糙度小于10 nm.通过二维扫描和光场重构,在油中获得了波长为532 nm的纵向偏振焦斑光强分布,焦斑半高全宽为0.27λ.该方法的分辨率主要取决于刀口的厚度和粗糙度引起的边缘散射以及空间扫描分辨率等因素.与基于纳米探针扫描的检测方法类似,刀口法扫描速度较慢,而且对空间扫描分辨率、重复定位精度和刀口粗糙度有较高要求.

7.3 基于宽视场大数值孔径显微镜的超振荡光场表征技术

探针法和刀口法均需要将检测单元直接与被检测光场接触,因此容易对被检测场造成影响,这是接触式测量难以克服的缺点.超振荡光场是由传播波相干叠加而成,其超振荡光场结构信息可以被传播到远场[41],因此可通过宽视场、大数值孔径显微镜对超振荡亚波长光场结构进行放大和测量[139].其最大的优点是探测装置无需与被检测光场直接接触,因此测量本身不会对被检测的超振荡光场产生影响.2012年,Zheludev研究团队[18]采用该方法在油中对波长为640 nm、半高全宽为185 nm(0.77倍衍射极限)的超振荡聚焦光场进行了测量.2014年,该研究团队采用此方法[122]获得了波长为405 nm圆偏振光的长焦深超衍射光场强度分布,焦斑半高全宽约为182 nm.2015年,新加坡国立大学和中国科学院光电所研究团队[125]采用该方法获取了波长为633 nm的长焦深超衍射光场强度分布,最小焦斑半高全宽为265 nm. 2017年,重庆大学研究团队采用该方法对波长为632.8 nm的角向偏振超振荡空心光针进行了实验测试,获得的空心光针内径最小值为215 nm(0.62倍衍射极限).采用此方法对超振荡光场进行测量,其能分辨的最小超振荡场尺寸受限于显微镜数值孔径、放大倍数和所使用探测器的空间分辨率.在数值孔径为1的极端理想条件下,显微镜放大倍数和探测器像素尺寸将决定所能测量的最小焦斑尺寸,而不受衍射极限制约.然而,由于传统显微成像系统的偏振滤波特性[132,139],尤其在采用大数值孔径、高放大倍数显微镜的情况下,难以对纵向偏振光场进行成像,因此无法实现对纵向光场的测量.

目前的文献报道中实验结果与理论设计结果上的差异,一方面是源于加工误差和实验光路误差,另一方面则是由光场测试方法本身所导致.由于超振荡光场中的超分辨精细结构是精确相干所形成,接触式测量必然会对被检测光场产生一定影响.特别是在深亚波长超振荡光场的测量中,接触式测量对超振荡光场分布的影响将无法忽略.而且,目前常用的接触式和非接触式测量方法,普遍存在偏振选择性,难以满足复杂矢量光场的测试要求.

8 光学超振荡器件的应用

与传统的成像透镜不同,超振荡透镜是利用相干光场的精确相干叠加形成超分辨焦斑.然而,理论研究和实验研究均表明[140],类似于传统透镜,特别是在旁瓣较小的情况下,超振荡聚焦透镜可以直接作为成像透镜使用,而且其点扩散函数半高全宽小于衍射极限.现有超振荡透镜自身的一些特性(如旁瓣大、效率较低等)曾一度被认为是其在成像应用中的最大障碍.然而,近年来的研究表明[56,60],在一维和二维超振荡光学现象中,超振荡区域和高幅值边带区域可以被分得足够开,以满足超分辨光学应用的需求;同时,对于效率较低的问题,可以通过高灵敏度探测方法得到较好的解决.已报道的单光子超振荡实验表明[102]：光学超振荡可以被应用于弱光、甚至是单光子计数条件下的远场超分辨成像.因此,超振荡光场和超振荡光学器件可能在非标记远场超分辨成像、超高密度数据存储等应用中具有极大的潜力和良好的前景.

8.1 非标记远场超分辨光学显微

由于微纳结构对于超振荡聚焦光场分布具有较大的影响,同时,超振荡光场可以被传统显微镜放大成像,因此,可以将超振荡聚焦光场作为显微照明光源,通过检测超振荡聚焦光场的变化,实现非标记的远场超分辨光学显微.更为重要的是,这种超分辨显微技术并不受超振荡焦斑旁瓣的影响,而且聚焦效率也不影响其作为照明光源使用. 2013年,Zheludev研究团队[18]在可见光640 nm单波长实验演示了基于超振荡聚焦光场的超分辨显微技术,尽管该超振荡焦斑主瓣强度小于紧邻的旁瓣强度,但仍然在实验上实现了优于λ/6的横向空间分辨率,而且理论上这种技术不存在分辨率极限.2016年,新加坡国立大学洪明辉研究团队[141]在可见光405 nm单波长利用超振荡亚波长光针作为照明光源(光针横向尺寸约为0.41λ,轴向长度12λ,旁瓣小于主瓣的20%),在实验上实现了0.16λ的横向空间分辨率.尽管采用超振荡光针有利于二维成像,但会极大地降低成像的轴向分辨率,目前尚无法实现三维超分辨成像.2016年,日本东北大学Matsunaga等[142]将超振荡光学聚焦应用于共焦激光扫描显微系统中,将系统点扩散函数半高全宽降低了近一半,有效地提升了系统的空间分辨率.

8.2 非标记远场超分辨光学成像

2012年,多伦多大学Piché等[143]基于本征模相干叠加,采用4f光学系统和空间光调制器,实现了远场超分辨成像,将分辨率在瑞利极限的基础上提高了45%.2013年,多伦多大学Amineh和Eleftheriades[20]基于超向天线思想,采用车比雪夫多项式,设计了一种超振荡滤波器,利用该滤波器可以实现二维和三维图像超分辨重建.2015年,罗先刚研究团队[144]采用二值相位板对光学望远系统点扩散函数半高全宽进行压缩,实现了具有超振荡特性的点扩散函数.并将其应用于非相干望远镜系统,实现了实时超分辨成像,成像分辨率为0.55倍瑞利极限.尽管其成像视场较小,然而在实际应用中,可以通过图像拼接的方式,实现较大视场的非标记远场超分辨成像.值得一提的是,该技术把超振荡概念拓展到了非相干成像系统,实现了非相干的非标记远场超分辨成像.

8.3 超高密度数据存储

2014年,南洋理工大学和南安普顿大学[145]共同提出了一种基于超振荡透镜的热辅助磁性写入技术.为了降低旁瓣,同时为了提高透镜对固体浸没薄膜厚度的冗余度,该超振荡聚焦透镜采用了超振荡光针设计.该透镜等效数值孔径达到了4.17,对波长为473 nm圆偏振光聚焦,透镜焦距为8µm,焦斑横向尺寸小于50 nm,焦深为5λ.由于焦深较大,其难以实现三维的高密度数据存储.

如前所述,目前报道的超振荡光场、尤其是单色超振荡光场仅能在二维平面内实现光学超分辨[60].如何实现三维的超振荡光场、构建三维超振荡点扩散函数,是实现三维超分辨光学显微、成像以及光存储的关键.

9 结 论

光学超振荡为从器件层面突破衍射极限瓶颈、研制新型的远场超分辨成像系统提供了一种崭新的途径.尽管光学超振荡现象和超振荡光学器件等相关研究得到了快速的发展,然而,在光学超振荡相关理论、超振荡光学器件设计与制作、超振荡光场测试技术以及相关应用等方面,尚面临很多亟待解决的重大科学技术问题.

在超振荡光场的构建方法和超振荡器件的设计方法等方面,目前仍然依赖优化算法,而且缺乏系统的设计理论,特别是如何解决设计中超振荡光场结构尺寸、旁瓣、视场以及效率等方面之间的矛盾以及如何实现三维超振荡光场等,还有待深入研究;在超振荡光学器件的实现方面,有赖于对光场振幅、相位、偏振、轨道角动量等参数的精确调控,重点需要解决在亚波长尺度下高效的光场多参量(振幅、相位、偏振等)同时调控;在超振荡光学器件的制备方面,急需突破跨尺度、大面积、多层亚波长结构阵列的高精度加工工艺等;在超振荡光场测试表征方面,如何实现深亚波长矢量光场电场分量、相位、轨道角动量的精确测量,以及如何完善对测试结果诠释等,都亟待开展深入研究.

尽管面临诸多挑战,超振荡光学器件在远场超分辨显微、成像和超高密度数据存储等方面,已初步显示出良好的应用前景.随着光学超振荡、超振荡光学器件及系统的相关理论和技术研究的不断深入,有望在光学器件层面突破衍射极限制约,推动超分辨显微、超分辨成像、光学纳米操控、纳米光学加工、超高密度数据存储、激光聚焦等技术进一步发展.

[1]Abbe E 1873 Archiv für Mikroskopische Anatomie 9 413

[2]Gan F X,Wang Y 2011 Opt.31 0900104(in Chinese) [干福熹,王阳2011光学学报31 0900104]

[3]Yoshiki K,Ryosuke K,Hashimoto M Hashimoto N, Araki T 2007 Opt.Lett.32 1680

[4]Terakado G,Watanabe K,Kano H 2009 Appl.Opt.48 1115

[5]Bergmans J W M 1996 Digital Baseband Transmission and Recording(Berlin：Springer Science&Business Media)pp74–86

[6]Gan Z S,Cao Y Y,Evans R A,Gu M 2013 Nat.Commun.4 2061

[7]Lubeck E,Cai L 2012 Nat.Methods 9 743

[8]Nägerl U V,Sibarita J B 2016 Neurophotonics 3 041801

[9]Pohl D W,Denk W,Lanz M 1984 Appl.Phys.Lett.44 651

[10]Pertsinidis A,Zhang Y X,Chu S 2010 Nature 466 647

[11]Betzig E,Patterson G H,Sougrat R,Lindwasser O W, Olenych S,Bonifacino J S,Davidson M W,Lippincott-Schwartz J,Hess H F 2006 Science 313 1642

[12]Rust M J,Bates M,Zhuang X W 2006 Nat.Methods 3 793

[13]Wildanger D,Medda R,Kastrup L,Hell S W 2009 J. Microsc.236 35

[14]Gustafsson M G L,Shao L,Carlton P M,Wang C J R, Golubovskaya I N,Cande W Z,Agard D A,Sedat J W 2008 Biophys.J.94 4957

[15]Rho J,Ye Z L,Xiong Y,Yin X B,Liu Z W,Choi H, Bartal G,Zhang X 2010 Nat.Commun.1 143

[16]Iwanaga M 2014 Appl.Phys.Lett.105 053112

[17]Srituravanich W,Pan L,Wang Y,Sun C,Bogy D B, Zhang X 2008 Nat.Nanotechnol.3 733

[18]Rogers E T F,Lindberg J,Roy T,Savo S,Chad J E, Dennisand M R,Zheludev N I 2012 Nat.Mater.11 432

[19]Wong A M H,Eleftheriades G V 2013 Sci.Rep.3 1715

[20]Amineh R K,Eleftheriades G V 2013 Opt.Express 21 8142

[21]Huang F M,Chen Y F,Javier Garcia de Abajo F,Zheludev N I 2007 J.Opt.A:Pure Appl.Opt.9 S285

[22]Rogers E T F,Zheludev N I 2013 J.Opt.15 094008

[23]Torraldo di Francia G 1952 Nuovo Cimento Suppl.9 426 [24]Frieden B R 1969 Opt.Acta 16 795

[25]Bucklew J A,Saleh B E A 1985 J.Opt.Soc.Am.A 2 1233

[26]Zheludev N I 2008 Nat.Mater.7 420

[27]Aharonov Y,Albert D Z,Vaidman L 1988 Phys.Rev. Lett.60 1351

[28]Aharonov Y,Anandan J,Popescu S,Vaidman L 1990 Phys.Rev.Lett.64 2965

[29]Berry M V,Popescu S 2006 J.Phys.A 39 6965

[30]Makris K G,Papazoglou D G,Tzortzakis S 2017 J.Opt. 19 014003

[31]Ferreira P J S G,Kempf A 2006 IEEE Trans.Signal Process.54 3732

[32]Huang F M,Zheludev N I,Chen Y F,Javier Garcia de Abajo F 2007 Appl.Phys.Lett.90 091119

[33]Chojnacki L,Kempf A 2016 J.Phys.A:Math.Theor. 49 505203

[34]Wen Z Q,He Y H,Li Y Y,Chen L,Chen G 2014 Opt. Express 22 22163

[35]Dennis M R,Hamilton A C,Courtial J 2008 Opt.Lett. 33 2976

[36]Berry M V,Dennis M R 2008 J.Phys.A:Math.Theor. 42 022003

[37]Huang K,Ye H P,Teng J H,Yeo S P,Luk’yanchuk B, Qiu C W 2014 Laser Photon.Rev.8 152

[38]Wong A M H,Eleftheriades G V 2011 IEEE Trans.Microw.Theory Tech.59 2173

[39]Eliezer Y,Hareli L,Lobachinsky L,Froim S,Bahabad A 2016 CLEO:QELS_Fundamental Science San Jose, California,United States,June 5–10,2016 FF1A.1

[40]Eliezer Y,Bahabad A 2014 Opt.Express 22 31212

[41]Cox I J,Sheppard C J R,Wilson T 1982 J.Opt.Soc. Am.72 1287

[42]Wei N,Gong M L,Cui,R Z 2003 Jpn.J.Appl.Phys. 42 104

[43]Sales T R M,Morris G M 1997 Opt.Lett.22 582

[44]Liu H T,Yan Y B,Jin G F 2005 J.Opt.Soc.Am.A 22 828

[45]Richards B,Wolf E 1959 Proc.R.Soc.London Ser.A 253 358

[46]Jabbour T G,Kuebler S M 2008 Opt.Lett.33 1533

[47]Huang F M,Zheludev N I 2009 Nano Lett.9 1249

[48]Wang X,Fu J,Liu X,Tong L M 2009 J.Opt.Soc.Am. A 26 1827

[49]Wong A M H,Eleftheriades G V 2010 IEEE Antennas Wirel.Propag.Lett.9 315

[50]Mazilu M,Baumgartl J,Kosmeier S,Dholakia K 2011 Opt.Express 19 933

[51]Baumgartl J,Kosmeier S,Mazilu M,Rogers E T F,Zheludev N I,Dholakia K 2011 Appl.Phys.Lett.98 181109

[52]Jin N B,Rahmat-Samii Y 2007 IEEE Trans.Antennas Propag.55 556

[53]Chen Z H,Zhang Y,Xiao M 2015 J.Opt.Soc.Am.B 32 1731

[54]Lin J,Zhao H Y,Ma Y,Tan J B,Jin P 2016 Opt.Express 24 10748

[55]Green field E,Schley R,Hurwitz I,Nemirovsky J,Makris K G,Segev M 2013 Opt.Express 21 13425

[56]Wong A M H,Eleftheriades G V 2015 Sci.Rep.5 8449

[57]Chremmos I,Fikioris G 2015 Opt.Commun.356 482

[58]Yu Y Z,Zhan Q W 2015 Opt.Express 23 7527

[59]Eliezer Y,Bahabad A 2016 ACS Photon.3 1053

[60]Wong A M H,Eleftheriades G V 2017 Phys.Rev.B 95 075148

[61]Diao J S,Yuan W Z,Yu Y T,Zhu Y C,Wu Y 2016 Opt. Express 24 1924

[62]Deng D M,Guo Q 2007 Opt.Lett.32 2711

[63]Carter W H 1972 J.Opt.Soc.Am.62 1195

[64]Lia J,Zhu S,Lu B 2009 Opt.Commun.282 4475

[65]Richards B,Wolf E 1959 Proc.R.Soc.Lond.A:Math. Phys.Sci.253 358

[66]Liu T,Liu Q,Yang S M,Jiang Z D,Wang T,Zhang G F 2017 Appl.Opt.56 3725

[67]Chen G,Li Y Y,Yu A P,Wen Z Q,Dai L R,Chen L, Zhang Z H,Jiang S L,Zhang K,Wang X Y,Lin F 2016 Sci.Rep.6 29068

[68]Liu T,Tan J B,Liu J,Wang H T 2013 Opt.Express 21 090

[69]Chen G,Wu Z X,Yu A P,Zhang Z H,Wen Z Q,Zhang K,Dai L R,Jiang S L,Li Y Y,Chen L,Wang C T,Luo X G 2016 Sci.Rep.6 37776

[70]Yu A P,Chen G,Zhang Z H,Wen Z Q,Dai L R,Zhang K,Jiang S L,Wu Z X,Li Y Y,Wang C T,Luo X G 2016 Sci.Rep.6 38859

[71]Ta fl ove A,Hagness S 2005 Computational Electrodynamics:The Finite Di ff erence Time-Domain Method (3rd Revised edition).(Boston：Artech House Publishers)pp2–3

[72]Ma X K 2016 The Electromagnetic Field Finite Element Combined with Analytical Method(Vol.1)(Beijing：Science Press)pp11–15(in Chinese)[马西奎2016电磁场有限元与解析结合解法(第1版)(北京：科学出版社)第11—15页]

[73]Magni V,Cerullo G,Silvestri S D 1992 Opt.Soc.Am. A 9 2031

[74]Knockaert L 2000 IEEE Trans.Signal Process.48 1695

[75]Zhang D W,Yuan X C,Ngo N Q,Shum P 2002 Opt. Express 10 521

[76]Liu T,Wang T,Yang S M,Sun L,Jiang Z D 2015 Opt. Express 23 32139

[77]Zhang L,Mei S T,Huang K,Qiu C W 2016 Adv.Opt. Mater.4 818

[78]Crozier K B,Sundaramurthy A,Kino G S,Quate C F 2003 Appl.Phys.94 4632

[79]Yu N F,Genevet P,Kats M A,Aieta F,Tetienne J P, Capasso F,Gaburro Z 2011 Science 334 333

[80]Li Z Y,Yu N F 2013 Appl.Phys.Lett.102 131108

[81]Pors A,Nielsen M G,Eriksen R L,Sergey I,Bozhevolnyi S I 2013 Nano Lett.13 829

[82]Yifat Y,Eitan M,Iluz Z,Boag A,Hanein Y,Scheuer J 2014 Int.Soc.Opt.Photon.8994 899416

[83]Arbabi A,Horie Y,Ball A J,Bagheri M,Faraon A 2015 Nat.Commun.6 7069

[84]Khorasaninejad M,Chen W T,Devlin R C,Oh J,Zhu A Y,Capasso F 2016 Science 352 1190

[85]Bomzon Z,Kleiner V,Hasman E 2001 Appl.Phys.Lett. 79 1587

[86]Jiang Z H,Lin L,Ma D,Yun S,Werner D H,Liu Z, Mayer T S 2014 Sci.Rep.4 7511

[87]Jiang S C,Xiong X,Hu Y S,Hu Y H,Ma G B,Peng R W,Sun C,Wang M 2014 Phys.Rev.X 4 021026

[88]Wang S Y,Zhan Q W 2016 Sci.Rep.6 29626

[89]Heckenberg N R,McDu ffR,Smith C P,White A G 1992 Opt.Lett.17 221

[90]Chen S M,Cai Y,Li G X,Zhang S,Cheah K W 2016 Laser Photon.Rev.10 322

[91]Li X,Pu M B,Zhao Z Y,Ma X L,Jin J J,Wang Y Q, Gao P,Luo X G 2016 Sci.Rep.6 20524

[92]Guo Y H,Pu M B,Zhao Z Y,Wang Y L,Jin J J,Gao P,Li X,Ma X L,Luo X G 2016 ACS Photon.3 2022

[93]Lin J,Genevet P,Kats M A,Antoniou N,Capasso F 2013 Nano Lett.13 4269

[94]Liu H,Yan Y,Yi D,Jin G 2003 Appl.Opt.42 1463

[95]Jabbour T G,Kuebler S M 2006 Opt.Express 14 1033

[96]Wong A M H,Eleftheriades G V 2011 IEEE Trans.Antennas Propag.59 4766

[97]He Y H,Wen Z Q,Chen L,Li Y Y,Ning Y Z,Chen G 2014 IEEE Photon.Technol.Lett.26 1801

[98]Wan X W,Shen B,Menon R 2014 J.Opt.Soc.Am.A 31 B27

[99]Maklizi M E I,Hendawy M,Swillam M A 2014 J.Opt. 16 105007

[100]Chen G,Li Y Y,Wang X Y,Wen Z Q,Lin F,Dai L R, Chen L,He Y H,Liu S 2016 IEEE Photonics Technol. Lett.28 335

[101]Chen G,Zhang K,Yu A P,Wang X Y,Zhang Z H,Li Y Y,Wen Z Q,Chen L,Dai L R,Jiang S L,Lin F 2016 Opt.Express 24 11002

[102]Yuan G H,Vezzoli S,Altuzarra C,Rogers E T F, Couteau C,Soci C,Zheludev N I 2016 Light:Sci.Appl. 5 e16127

[103]Stanley S H,Berthold K P H,Dennis M F,Michael S M 2006 Appl.Phys.Lett.88 261107

[104]Zhang M G,Du J L,Shi H F,Yin S Y,Xia L P,Jia B H,Gu M,Du C L 2010 Opt.Express 18 14664

[105]Venugopalan P,Zhang Q M,Li X P,Kuipers L,Gu M 2014 Opt.Lett.39 5744

[106]Liu Y X,Xu H,Stief F,Zhitenev N,Yu M 2011 Opt. Express 19 20233

[107]Roy T,Rogers E T F,Zheludev N I 2013 Opt.Express 21 7577

[108]Liu T,Shen T,Yang S M,Jiang Z D 2015 J.Opt.17 035610

[109]Tang D L,Wang C T,Zhao Z Y,Wang Y Q,Pu M B, Li X,Gao P,Luo X G 2015 Laser Photon Rev.9 713

[110]Yu A P,Cao L Y,Wu Z X,Wen Z Q,Chen G 2016 National Conference on Opto-Mechanical-Electrical TechnologiesandSystems& OptoelectronicTechnology Committee of China Optical Society/Chinese Institute of Instrumentation Branch of Optical-Mechanical-Member Conference Guilin,China,Oct.14–17,2016, gdjs2016-2016-1149(in Chinese)[余安平,曹璐瑶,武志翔,温中泉,陈刚 2016全国光机电技术及系统学术会议暨中国光学学会光电技术专委会/中国仪器仪表学会光机电分会会员代表大会中国桂林,2016年10月14日—17日, gdjs2016-2016-1149]

[111]Li Y,Li X,Pu M B,Zhao Z Y,Ma X L,Wang Y Q, Luo X G 2016 Sci.Rep.6 19885

[112]Li M Y,Li W L,Li H Y,Zhu Y C,Yu Y T 2017 Sci. Rep.7 1335

[113]Wu M X,Chen R,Soh J H,Shen Y,Jiao L S,Wu J F, Chen X D,Ji R,Hong M H 2016 Sci.Rep.6 31637

[114]Dorn R,Quabis S,Leuchs G 2003 Phys.Rev.Lett.91 233901

[115]Kozawa Y,Sato S 2007 J.Opt.Soc.Am.A 24 1793

[116]Luo J,Zhao Z Y,Pu M B,Yao N,Tang D L,Gao P, Jin J J,Li X,Wang C T,Yu H L,Luo X G 2015 Opt. Commun.356 445

[117]Stafeev S S,Nalimov A G,Kotlyar M V,Gibson D,Song S,O’Faolain L,Kotlyar V V 2016 Opt.Express 24 29800

[118]David A,Gjonaj B,Blau Y,Dolev S,Bartal G 2015 Optica 2 1045

[119]Wang H F,Shi L P,Yanchuk B L,Sheppard C,Chong C T 2008 Nat.Photon.2 501

[120]Ye H P,Qiu C W,Huang K,Teng J H,Luk’yanchuk B, Yeo S P 2013 Laser Phys.Lett.10 065004

[121]Rogers E T F,Savo S,Lindberg J,Roy T,Dennis M R, Zheludev N I 2013 Appl.Phys.Lett.102 031108

[122]Yuan G H,Rogers E T F,Roy T,Adamo G,Shen Z X, Zheludev N I 2014 Sci.Rep.4 6333

[123]Peng R B,Li X,Zhao Z Y,Wang C T,Hong M H,Luo X G 2014 Plasmonics 9 55

[124]Chávez-Cerda S,Pu J X 2015 J.Opt.Soc.Am.A 32 1209

[125]Qin F,Huang K,Wu J F,Jiao J,Luo X G,Qiu C W, Hong M H 2015 Sci.Rep.5 09977

[126]Liu T,Wang T,Yang S M,Jiang Z D 2016 Opt.Commun.372 118

[127]Guan J,Lin J,Chen C,Ma Y,Tan J B,Jin P 2017 Opt. Commun.doi：http：//dx.doi.org/10.1016/j.optcom.2017. 04.003

[128]Yu W T,Ji Z H,Dong D S,Yang X S,Xiao Y F,Gong Q H,Xi P,Shi K B 2016 Laser Photon Rev.10 147

[129]Makris K G,Psaltis D 2011 Opt.Lett.36 4335

[130]Wu J,Wu Z X,He Y H,Yu A P,Zhang Z H,Wen Z X, Chen G 2017 Opt.Express 25 6274

[131]Lee W H 1979 Appl.Opt.18 3661

[132]Grosjean T,Courjon D 2003 Phys.Rev.E 67 046611

[133]Adam P M,Royer P,Laddada R,Bigeon J L 1998 Appl. Opt.37 1814

[134]Novotny L,Beversluis M R,Youngworth K S,Brown T G 2001 Phys.Rev.Lett.86 5251

[135]Dorn R,Quabis S,Leuchs G 2003 Phys.Rev.Lett.91 233901

[136]Kitamura K,Sakai K,Noda S 2010 Opt.Express 18 4518

[137]Born M,Wolf E 1999 Principles of Optics(Vol.7)(New York：Cambridge University Press)pp221–223

[138]Yang L X,Xie X S,Wang S C,Zhou J Y 2013 Opt.Lett. 38 1331

[139]Liu T,Yang S M,Jiang Z D 2016 Opt.Express 24 16297

[140]Roy T,Rogers E T F,Yuan G H,Zheludev N I 2014 Appl.Phys.Lett.104 231109

[141]Qin F,Huang K,Wu J F,Teng J H,Qiu C W,Hong M H 2016 Adv.Mater.29 1602721

[142]Matsunaga D,Kozawa Y,Sato S 2016 CLEO:QELS_ FundamentalScienceSanJose,California,United States,June 5–10,2016 STh4G.8

[143]Piché K,Leach J,Johnson A S,Salvail J Z,Kolobov M I,Boyd R W 2012 Opt.Express 20 26424

[144]Wang C T,Tang D L,Wang Y Q,Zhao Z Y,Wang J, Pu M B,Zhang Y D,Yan W,Gao P,Luo X G 2015 Sci. Rep.5 18485

[145]Yuan G H,Rogers E T F,Roy T,Shen Z X,Zheludev N I 2014 Opt.Express 22 6428

PACS:42.25.—p,42.79.—e,07.60.—j,78.67.Pt DOI:10.7498/aps.66.144205

Optical super-oscillation and super-oscillatory optical devices∗

Chen Gang†Wen Zhong-Quan Wu Zhi-Xiang
(Key Laboratory of Optoelectronic Technology and Systems,Ministry of Education,College of Optoelectronic Engineering,
Chongqing University,Chongqing 400044,China)

29 March 2017;revised manuscript

24 May 2017)

The di ff raction limit of traditional optical device greatly restricts the further development of optical super-resolution systems.It is a great challenge to overcome the di ff raction limit at a device level,and achieve label-free far- field superresolution imaging.Optical super-oscillation provides a new way to realize super-resolution since it allows the generation of arbitrary small structures in optical fields in the absence of evanescent waves.The researches of optical super-oscillation and super-oscillatory optical devices have grown rapidly in recent decades.Optical super-oscillation and super-oscillatory optical devices have been demonstrated theoretically and experimentally to show great potential applications in labelfree far- field optical microscopy,far- field imaging and high-density data storage.In this paper,we gives a broad review of recent development in optical super-oscillation and super-oscillatory optical devices,including basic concepts,design tools and methods,testing techniques for super-oscillatory optical field,and their applications.

super-oscillation,super-resolution,di ff ractive devices,sub-wavelength

:42.25.—p,42.79.—e,07.60.—j,78.67.Pt

10.7498/aps.66.144205

∗国家重点基础研究发展计划(批准号：2013CBA01700)、国家自然科学基金(批准号：61575031,61177093)和教育部“新世纪优秀人才支持计划”(批准号：NCET-13-0629)资助的课题.

†通信作者.E-mail：gchen1@cqu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Basic Research Program of China(Grant No.2013CBA01700),the National Natural Science Foundation of China(Grant Nos.61575031,61177093),and the Program for New Century Excellent Talent in University,China(Grant No.NCET-13-0629).

†Corresponding author.E-mail：gchen1@cqu.edu.cn