铁冲击相变的晶向效应∗
李俊吴强 于继东 谭叶 姚松林 薛桃 金柯
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理实验室,绵阳 621900)
铁冲击相变的晶向效应∗
李俊†吴强 于继东 谭叶 姚松林 薛桃 金柯
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理实验室,绵阳 621900)
(2017年1月2日收到;2017年4月12日收到修改稿)
采用基于火炮加载的三样品精细波剖面对比测量,研究了晶向效应对铁弹-塑性转变及体心立方结构(bcc,α相)至六角密排结构(hcp,ε相)相变特性的影响.观测到单晶铁异常的弹-塑性转变行为,这与基于位错密度描述的黏塑性本构模型计算结果相符,对应的Hugoniot弹性极限δHEL均大于6 GPa,且具有晶向相关性,即δ111HEL>δ110HEL>δ100HEL;系统获取了相变起始压力PPT晶向相关性的实验数据,[100],[110]和[111]晶向的PPT实测值分别为13.89±0.57 GPa,14.53±0.53 GPa,16.05±0.67 GPa,其变化规律与非平衡分子动力学计算结果相符.上述结果揭示出冲击压缩下单晶铁存在塑性与相变微观机理的强耦合,为完善用于冲击实验描述的相场动力学模型提供了重要的实验支撑.
相变,弹-塑性转变,晶向效应,铁
1 引 言
作为地球内、外核的主要成分和工业领域重要的应用材料,铁在高温高压下呈现出多种物相结构,包括α相(体心立方,bcc),γ相(面心立方,fcc), ε相(六角密排,hcp),以及一些可能存在但尚未确定的相结构[1].因此,铁在高温高压下的物性和相结构特性(包括物态方程、固-液熔化、固-固相变等)一直是高压物理领域的研究热点,不仅有助于深化我们对地球、天体物理的认识,而且有助于推动材料科学、凝聚态物理、高压物理等学科的发展.铁从体心立方结构至六角密排结构的相变行为是研究最早、最广泛的例子.自1956年Minshall等[2,3]首次在冲击压缩条件下发现铁多型相变,开辟冲击相变研究的新方向以来,人们已开展了大量相关的实验研究和理论探索,获取了相结构、相变序列和相界等信息[4-6],还观测到与动力学有关的非平衡相变特征[7-24].但是由于缺乏更为系统、深入的实验诊断和数值模拟能力,对相变动力学微观物理机理及影响因素(如初始温度、压力幅度、加载速率、单晶晶向等如何影响相变波剖面细观特征及转变速率)仅有一些初步的认识,且仍然存在争议.其中,铁冲击相变的晶向效应是近年来人们关注较多且有待澄清的基本科学问题之一.
铁的晶向效应研究始于2002年Kadau等[14-16]的报道,他们利用百万原子量级的非平衡分子动力学模拟(NEMD)研究不同晶向铁在相变过程中双波结构的形成以及相变成核的微观特征.研究发现,相变压力与单晶铁的晶向密切相关,即沿[100],[110],[111]晶向的相变阈值压力分别为15,17,20 GPa;且不同晶向的相转变路径及机理也存在差异,即[100]晶向为有序转变,高压相为hcp结构,相变主导机理为相邻原子的马氏体转变(母相与子相有固定的晶体取向关系),对应渡越时间约为50 ps,而[110],[111]晶向的转变则存在大量fcc亚稳态结构,相转变的渡越时间更长.后来,王昆等[17]、卢志鹏等[18]在计算中进一步考虑了塑性变形与相转变过程的耦合,得到沿[001],[110]和[111]晶向的相变压力分别为18.0,22.3,23.8 GPa,并认为Kadau等NEMD模拟中出现fcc亚稳态结构有可能是势函数造成的一种假象.不难看出,上述理论计算预测了单晶铁相变特性及其微观机理的差异,但仍有认识分歧,需要实验数据给予证实.但有关单晶铁的冲击实验数据少有报道.2009年Jensen等[21]曾开展了冲击加载下[100]晶向单晶铁的相变动力学研究,实验证实了单晶铁与多晶铁相变压力阈值的差异,获取[100]晶向铁α→ε相变起始压力为14.26 GPa,高于多晶铁(实测值为12.89 GPa).同时,他们利用基于反向碰撞法(即样品作为飞片直接撞击窗口)的波剖面测量,观测到α→ε相转变的迟滞特征,且渡越时间随碰撞压力呈非线性变化趋势,从碰撞压力在相变压力附近的百纳秒量级降低至18—20 GPa压力范围的亚纳秒量级.
由此可见,目前对于铁冲击相变的晶向效应研究尚缺乏系统性、规律性的认识,塑性变形如何影响相变特性?不同晶向的动态响应和相变机理是否存在差异(如[110]和[111]晶向的转变是否涉及NEMD模拟预测的亚稳态相)?针对这些问题还需开展更深入的研究工作.鉴于此,本文从单晶铁的精细相变波剖面和相变起始压力测量着手,将其作为甄别单晶铁晶向效应的第一步,系统地研究了[100],[110]和[111]晶向单晶铁的弹-塑性转变及相变动力学行为,为验证单晶铁冲击相变的晶向相关性、分析相变微观机理提供基础实验数据支撑.
2 实验方法
作为认识冲击相变的重要实验手段,精细波剖面测量可以提取相变压力、转变速率等重要信息.为此,单晶铁冲击实验采用了基于三样品对比法的波剖面测量,这种方法不仅可以保证实验加载条件的一致性,以更清楚地区分晶向效应的影响,而且可以有效地节约实验发数,提高实验耗费比.
实验装置及测试系统如图1所示,采用火炮加载方式(可控弹速范围0.3—1.5 km/s)进行一维平面冲击加载.实验所用飞片和窗口均为z切蓝宝石(Al2O3)单晶圆片,表面经光学抛光处理;单晶铁样品由德国MaTeck公司提供,包括[100],[110]和[111]三个晶向,由分子束外延法生长,纯度大于99.98%,样品圆片采用高功率激光束切割而成,晶向角偏差小于0.5°,表面粗糙度小于30 nm.实验中各部件的名义尺寸列于表1中,确保在有效观测时间内界面测量区域不受样品边侧稀疏波和飞片后界面追赶稀疏波的影响.测试系统包括多普勒光探针(DPS)和全光纤式激光干涉速度测量仪(DISAR)两部分,其中安装于靶前端面的DPS用于直接测量飞片速度w和击靶到达时刻t1,其速度测量相对不确定度小于0.5%.DISAR测试系统用于测量不同晶向单晶铁样品/z切Al2O3单晶窗口的界面速度历史,即当冲击波到达样品后端面时由于界面运动导致多普勒频移的发生,入射激光(中心波长1550 nm)与反射激光发生频域调制,解读频移信号即可得出样品的粒子速度,测试系统的时间分辨率可达50 ps,空间分辨率约为100µm.

表1 实验各部件的名义尺寸Table 1.The nominal sizes of the experimental parts.
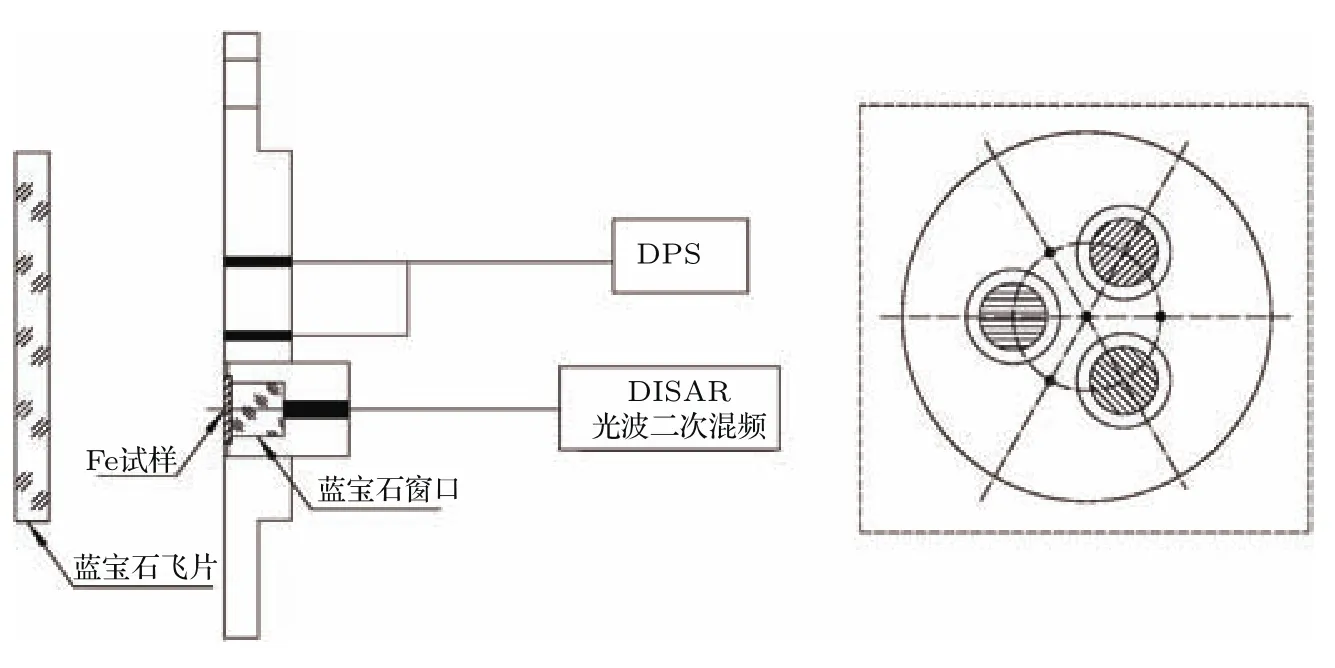
图1 单晶铁冲击实验装置及测试框图Fig.1.Experimental assembly and in-situ diagnostic of single crystal iron under shock compression.

图2 冲击相变测量原理 (a)相变波剖面示意图;(b)波系相互作用分析Fig.2.Shock Hugoniot measurement for the shockinduced phase transformation:(a)Schematic of wave pro fi le;(b)interaction analysis for shock wave.
对于发生冲击相变时的多波而言,Hugoniot状态的确定需要考虑波系的相互作用.图2(a)为典型的冲击相变波剖面,包含弹性前驱波(PEL波)、塑性波(P1波)和相变波(P2波),其中PEL波波速大于P1波,P1波波速大于P2波.PEL波与P1波的相互作用过程如图2(b)所示,根据波的传播特性(设定传播方向从左向右),首先右行的PEL波到达样品/窗口界面后(t2时刻),会反射回一个左行的稀疏波(波速为c1)并与随后的P1波迎面相遇,造成P1波强度略微下降.与此同时,又再次反射回一个右行的稀疏波(波速为c2),其传至界面后继续反射,以此反复形成复杂波系.根据文献[9,10],不考虑PEL波引起的熵增变化,反射波作为弹性波处理,在实验室坐标系下可得P1波波速US1为

式中uEL为PEL波界面粒子速度,t1为击靶时刻,h为样品厚度,Δh为界面在时间内移动的距离.通常情况下,冲击相变发生时弹性波的压力幅值会远小于塑性波,且弹-塑性转变过程极快,即 (1)式中由此可将PEL波波速cl,P1波波速US1和P2波波速US2写为
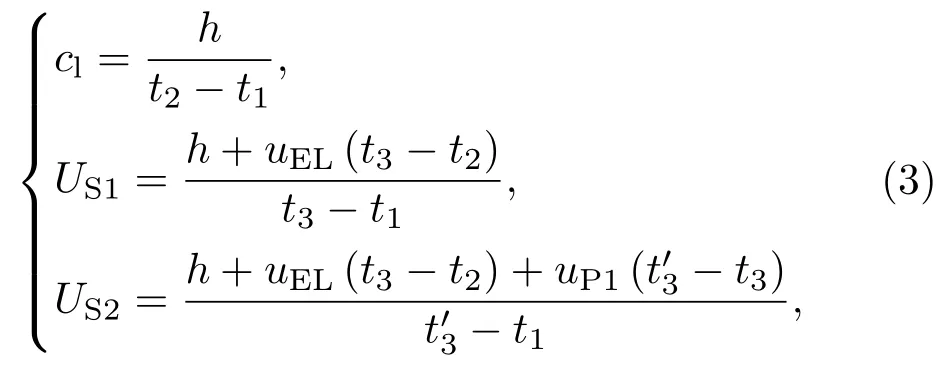
式中uP1为P1波界面粒子速度,t2,t3和t′3分别为PEL波、P1波和P2波到达时刻.再利用Rankine-Hugoniot方程,可得

式中ρ0为样品初始密度,下标HEL表示Hugoniot弹性极限,下标PT表示相变点,PPT为相变起始压力.特别需要指出的是,由于波系相互作用,相变发生时会伴有母相残余,使实测波剖面中P1波与P2波之间的上升沿发生展宽,对于平衡相变过程(即uP1稳定)可采用切线法确定t′3,而对于非平衡相变过程,这样的处理会带来较大偏差.
3 结果与讨论
在中国工程物理研究院流体物理研究所的37 mm口径火炮上,进行2发单晶铁(含多晶铁)的三样品对比实验.图3是典型的实验结果,可见击靶前飞片的运动速度为一个恒定值(871 m/s),确保了加载状态的稳定.实测界面速度剖面的精细特征均记录完备,其中PEL波展现出极高的粒子速度幅值及松弛特性,P1波则反映出与动力学相关的速度回跳特征,在后续章节中我们将做进一步分析和讨论.利用(3)式和(4)式获取的单晶铁Hugoniot弹性极限和相变起始压力实测值列于表2中,在所有实验压力范围内z切Al2O3单晶窗口均为弹性响应且具有良好冲击透明性,1550 nm波长对应的速度折射率修正因子为1.744[25].

图3 铁的多样品比对实验结果 (a)飞片击靶速度;(b)Fe/Al2O3界面速度剖面Fig.3.One-shot experimental results for contrasting three-independent iron samples:(a)Impact velocity for fl yer; (b)shock-wave pro fi les from all Fe/Al2O3interfaces.

表2 单晶铁冲击Hugoniot实验结果Table 2.Shock Hugoniot data of single-crystal iron.
3.1 弹-塑性转变与动态屈服
图4所示为实测波剖面中不同晶向单晶铁及多晶铁的弹性前驱波部分,其中x轴已作归一化处理(为时间t与样品厚度h的比值).从图中不难看出,与多晶铁不同的是,在单晶铁中可以观测到明显的弹性波传播以及弹-塑性转变的应力松弛现象,即弹性前驱波的加载应力先很快上升到暂稳态,然后逐渐松弛至准平衡态.上述现象在Jensen等[21]的[100]晶向单晶铁波剖面中并没有观测到,但是在高强度脆性晶体材料(如氯化钾、硫化镉)实验中曾有类似报道,并使冲击条件下相变和塑性的相互作用变得更为复杂.同时,单晶铁的弹性响应表现为各向异性,PEL波的粒子速度幅值为[100]晶向最大,[110]晶向次之,[111]晶向最小;结合样品厚度和到达时刻确定的波速则是[111]晶向最大,[110]晶向次之,[100]晶向最小;由此获取三个晶向单晶铁的Hugoniot弹性极限δHEL均大于6 GPa(表2).可见,单晶铁在冲击加载下有较高的屈服强度,远大于多晶铁(实验值约1.3 GPa),接近于理论计算的极限.这一观点也能够得到Hawreliak等[26]的动态X射线衍射实验数据的佐证,他们观测到[001]晶向单晶铁在冲击压力5.4 GPa时晶格响应仍为单一轴向压缩,仅有(001)bcc晶面发生了约4.1%的缩短,与我们的波剖面测量结果是符合的.

图4 (网刊彩色)单晶铁速度剖面比较(弹-塑性转变部分)Fig.4.(color online)Comparison of the wave pro fi les in single crystal iron(part of elastic-plastic deformation).
进一步对单晶铁弹-塑性转变的物理机理进行分析,图5所示为不同晶向单晶铁弹性前驱波的数值模拟结果.计算采用了文献[27,28]中提出的位错密度描述的黏塑性本构模型,不同晶向的冲击加载则选用同一输入参数,通过旋转刚度矩阵实现.图中除[111]晶向的粒子速度幅值略有差异之外,三个晶向弹性前驱波的实测值与模拟结果在波速及回跳特征上符合较好.结果表明,针对三个不同晶向,刚度矩阵在加载方向(计算中为x轴)的分量存在关系即三个晶向弹性前驱波波速也与之对应,实验与计算曲线均合理地体现了各向异性特征.不同晶向速度回跳的差异反映出弹-塑性转变应力松弛的晶向相关性,其应力松弛的强度会受弹性模型和Schmid因子共同影响,即同一厚度下弹性模量越大,位错演化的耗散能越大,应力松弛越快;同时Schmid因子越大,滑移系越易于启动.以[100]和[110]晶向为例,虽然沿加载方向的Schmid因子相同,但[110]晶向的弹性模量更大,使其应力松弛更强,则对应的Hugoniot弹性极限拐点更低.
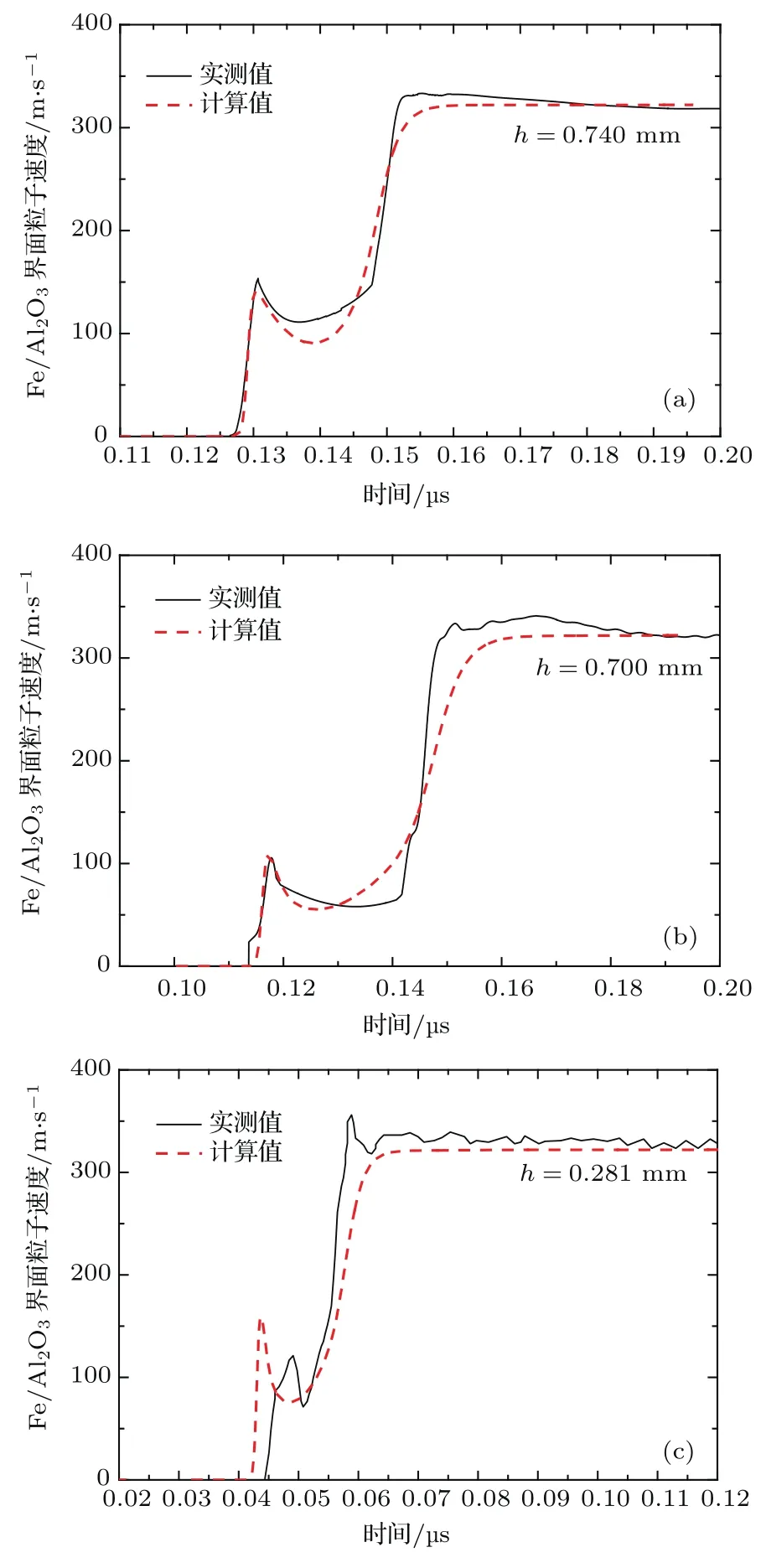
图5 不同晶向单晶铁弹性波实验与数值模拟的比较(a)[100]晶向;(b)[110]晶向;(c)[111]晶向Fig.5.Comparison of the experimental results and the numerical simulation results for the elastic wave in single crystal iron:(a)[100]orientation;(b)[110] orientation;(c)[111]orientation.
图6为实测单晶铁弹性前驱波的波速-粒子速度关系.对于[100]晶向,弹性前驱波实测值与Jensen等[21]报道中的理论预测线完全符合,而在文献[21]实测波剖面中未能观测到弹性前驱波的原因可能与VISAR测量精度及数据处理方法有关.对于[110]晶向和[111]晶向,实测数据与Kadau等[14-16]NEMD模拟中低压区弹性压缩曲线是符合的,且三个晶向弹性响应的基本变化规律也与之一致,从大到小顺序依次为[111]晶向、[110]晶向、[100]晶向.综上所述,我们通过波剖面测量首次观测到单晶铁中异于多晶铁的高强度动态屈服现象,极大的δHEL会不可避免地带来冲击相变与塑性的微观机理耦合,因而在NEMD计算中如何考虑和准确反映这一特征,是正确预测和理解铁α→ε相变过程中是否存在亚稳态fcc相以及晶向相关性的基础和关键问题之一.

图6 (网刊彩色)实测单晶铁弹性波波速-粒子速度Fig.6.(color online)Plots of the measured elastic wave velocity vs.the particle velocity for single crystal iron.
3.2 冲击相变与晶向效应
图7为实测波剖面中不同晶向单晶铁及多晶铁的塑性波部分,包括P1波和P2波.与弹性前驱波相似,单晶铁的相转变过程也表现出显著的晶向相关性,对应α→ ε相变起始点的粒子速度为[111]晶向最大,[110]晶向次之,[100]晶向最小,由此得到的相变起始压力-粒子速度(PPT-up)关系如图8所示.可见,实验测得[100]晶向单晶铁和多晶铁的PPT值分别为13.89±0.57 GPa和13.30±0.37 GPa,与文献[21]的实验结果(14.26± 0.14 GPa和12.89±0.15 GPa)相符;[110]晶向和[111]晶向的PPT实测值则为14.53±0.53 GPa和16.05±0.67 GPa,由此反映了单晶铁冲击相变的晶向相关性,其变化规律也与Kadau等[14-16]及王昆等[17]的NEMD计算结果相符合,但实测值更低.
此外,图7中P1至P2波的转变均有显著的速度回跳特征,反映了相变动力学效应(主导因素为相变动力学系数)对波剖面演化的影响.从其微观机理来看,相变过程中成核点处新相的生长将伴随对周围亚稳态区域的卸载作用,即成核点的生长抑制周围潜在成核点的生长,在相场模型中卸载作用的强弱由动力学系数决定,相同相变驱动力作用下,相边界速度越快(动力学系数越大),卸载作用越强,成核点生长对周围亚稳区域的卸载作用将带来成核密度及分布的变化.根据Smith等[22]的研究,可基于相变过程粒子速度的回跳获取α→ε相转变速率图9为相变起始压力随相转变速率的变化.可以清楚地看到,多晶铁的实验结果与Barker等[29]的冲击实验数据一致,均满足线性变化关系σα→ε=10.8+0.55ln单晶铁的实验结果则明显高于多晶铁,且具有晶向相关性,即


图7 (网刊彩色)单晶铁速度剖面比较(相变部分)Fig.7.(color online)Comparison of the wave pro fi les in single crystal iron(part of phase transformation).

图8 (网刊彩色)实测单晶铁相变压力-粒子速度Fig.8.(color online)Plots of the measured phasetransition onset pressure vs.the particle velocity for single crystal iron.
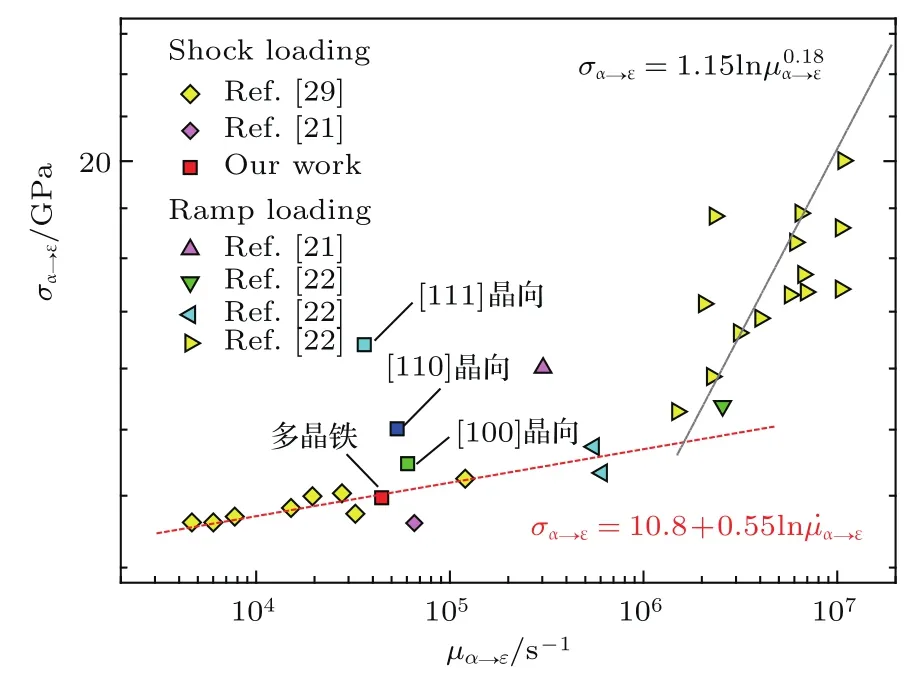
图9 (网刊彩色)相变起始压力随相转变速率的变化Fig.9.(color online)Plots of the onset pressure of phase transition vs.the strain-rate associated with the phase transition for single crystal iron.
4 结 论
本文开展了冲击载荷下单晶铁α→ ε相变特性研究,通过精细波剖面测量获取了晶向效应([100],[110]和[111]晶向)对塑性和相变特性影响的直接实验数据,得到以下结论.
1)首次观测到单晶铁异于多晶铁的高强度屈服行为,这与基于连续位错动力学模型的数值模拟结果相符,获取单晶铁的Hugoniot弹性极限均大于6 GPa且具有晶向相关性,即上述结果为认识单晶铁塑性响应与冲击相变微观机理的耦合提供了基础实验依据,因而在NEMD计算中对其进行正确描述有助于回答铁bcc到hcp结构相变起源以及亚稳态fcc相的争论.
2)获取[100]晶向、[110]晶向和[111]晶向的相变起始压力分别为13.89,14.53,16.05 GPa,其晶向相关性变化规律与NEMD计算结果符合,但实测值更低.同时,基于波剖面中相变波的速度回跳得到的单晶铁α→ε相转变速率高于多晶铁且具有晶向相关性,反映了相变动力学主导因素(即相变动力学系数)对波剖面演化的影响.上述结果为发展和完善用于冲击实验描述的相场动力学模型[30]提供了重要的实验支撑.
[1]Saxena S K,Shen G,Lazor P 1993 Science 260 1312
[2]Minshall S 1955 J.Appl.Phys.26 463
[3]Bancraft D,Peterson E L,Minshall S 1956 J.Appl.Phys.27 291
[4]Saxena S K,Dubrovinsky L S,Häggkvist P,Cerenius Y,Shen G,Mao H K 1995 Science 269 1703
[5]Belonoshko A B,Dorogokupets P I,Johansson B,Saxena S K,Koči L 2008 Phys.Rev.B 78 104107
[6]Tateno S,Hirose K,Ohishi Y,Tatsumi Y 2010 Science 330 359
[7]Crowhurst J C,Reed B W,Armstrong M R,Radousky H B,Carter J A,Swift D C,Zaug J M,Minich R W, Teslich N E,Kumer M 2014 J.Appl.Phys.115 113506
[8]Ma Y Z,Selvi E,Levitas V I,Hashemi J 2006 J.Phys.Condens.Matter 18 1075
[9]Johnson P C,Stein B A,Davis R S 1962 J.Appl.Phys.33 557
[10]Zaretsky E B 2009 J.Appl.Phys.106 023510
[11]Merkel S,Liermann H P,Miyagi L 2013 Acta.Materialia 61 5144
[12]Lu Z P,Zhu W J,Liu S J,Lu T C,Chen X R 2009 Acta Phys.Sin.58 2083(in Chinese)[卢志鹏,祝文军,刘绍军,卢铁城,陈向荣2009物理学报58 2083]
[13]Shao J L,He A M,Qin C S,Wang P 2009 Acta Phys. Sin.58 5610(in Chinese)[邵建立,何安民,秦承森,王裴2009物理学报58 5610]
[14]Kadau K,Germann T C,Lomdahl P S,Holian B L 2002 Science 296 1681
[15]Kadau K,Germann T C,Lomdahl P S,Holian B L 2005 Phys.Rev.B 72 064210
[16]Kadau K,Germann T C,Lomdahl P S,Albers R C, Wark J S,Higginbotham A,Holian B L 2007 Phys.Rev. Lett.98 135701
[17]Wang K,Xiao S F,Deng H Q,Zhu W J,Hu W Y 2014 Int.J.Plast.59 180
[18]Lu Z P,Zhu W J,Lu T C,Wang W Q 2014 Modelling Simul.Sci.Eng.22 025007
[19]Ma W,Zhu W J,Zhang Y L,Jing F Q 2011 Acta Phys. Sin.60 066404(in Chinese)[马文,祝文军,张亚林,经福谦2011物理学报60 066404]
[20]Shao J L,Qin C S,Wang P 2009 Acta Phys.Sin.58 1936(in Chinese)[邵建立,秦承森,王裴 2009物理学报58 1936]
[21]Jensen B J,Gray III G T,Hixson R S 2009 J.Appl. Phys.105 103502
[22]Smith R F,Eggert J H,Swift D C,Wang J,Du ff y T S,Braun D G,Rudd R E,Reisman D B,Davis J P, Knudson M D,Collins G W 2013 J.Appl.Phys.114 223507
[23]Yaakobi B,Boehly T R,Meyerhofer D D,Collins T J 2005 Phys.Rev.Lett.95 075501
[24]Kalantar D H,Belak J F,Collins G W,Colvin J D,Davis H M,E ff ert J H,Germann T C,Hawreliak J,Holian B L,Kadau K,Lomdahl P S,Lorenzana H E,Meyers M A,Rosolankova K,Schneider M S,Sheppard J,Stölken J S,Wark J S 2005 Phys.Rev.Lett.95 075502
[25]Cao X X,Li J B,Li J,Li X H,Xu L,Wang Y,Zhu W J, Meng C M,Zhou X M 2014 J.Appl.Phys.116 093516
[26]Hawreliak J A,El-Dasher B,Lorenzana H 2011 Phys. Rev.B 83 144114
[27]Krasnikov V S,Mayer A E,Yalovets P A 2011 Int.J. Plast.27 1294
[28]Mayer A E,Khishchenko K V,Levashov P R,Mayer P N 2013 J.Appl.Phys.113 193508
[29]Barker L M,Hollenbach R E 1974 J.Appl.Phys.45 4872
[30]Yu J D,Wang W Q,Wu Q 2012 Phys.Rev.Lett.109 115701
PACS:62.50.Ef,61.50.Ks,64.70.kd DOI:10.7498/aps.66.146201
Orientation e ff ect of alpha-to-epsilon phase transformation in single-crystal iron∗
Li Jun†Wu Qiang Yu Ji-Dong Tan Ye Yao Song-Lin Xue Tao Jin Ke
(Laboratory for Shock Wave Detonation Physics Research,Institute of Fluid Physics,China Academy of Engineering Physics, Mianyang 621900,China)
2 January 2017;revised manuscript
12 April 2017)
The dynamic response of iron,especially the phase transformation from the ambient body-centered-cubic(bcc) α-phase to the hexagonal-closed packed(hcp)ε-phase,has been studied extensively in the last 60 years due to its importance in industry and its role as a main constituent of Earth.Recently,this topic has attracted a lot of attention in the aspects of the kinetic characteristics and mechanism of the shock-induced α↔ ε phase transition,including orientation-,temperature-,time-and strain rate-dependences.But only a few data have been published on the crystal orientation e ff ect.The systematic experimental results to identify the predictions of the non-equilibrium molecular dynamics(NEMD)simulation are still lacking.For this reason,we study the shock responses of the[100],[110]and [111]orientated iron single crystals by using a three-independent-sample method in one shot.Unlike previously reported [001]single-crystal iron,a clear three-wave structure consisting of a PELwave(elastic wave),a P1wave(plastic wave) and a P2wave(phase transition wave)is observed in the measured wave pro fi les for all single-crystal iron samples. The elastic-plastic transition process is in accordance with the numerical simulation of dislocation-based constitutive model for visco-plastic deformation.It is found that the values of Hugoniot elastic limit δHEL(δ111HEL>δ110HEL>δ100HEL) are greater than 6 GPa and dependent on the initial crystal orientation.Such a high yield strength is consistent with the nanosecond X-ray di ff raction of[001]single-crystal iron where the uniaxial compression of the lattice has been observed at a shock pressure of about 5.4 GPa.Moreover,the onset pressures PPTfor the α→ε phase transition are obtained to be 13.89±0.57 GPa,14.53±0.53 GPa and 16.05±0.67 GPa along the[100],[110],and[111]directions, respectively.Based on these results,it is concluded that the crystal orientation e ff ect of PPTis consistent with the reported NEMD calculations.However,the measured values are lower.In addition,the transition strain-ratio of singlecrystal iron is found to be higher than that of polycrystalline iron,re fl ecting the in fl uence of the transformation kinetics (i.e.,transformation kinetics coefficient)on the wave pro fi le evolution.Our observations indicate that the strong coupling between plasticity and phase transition in single crystal iron might be a key point for understanding the origin of the phase transition and also for ending the controversy of metastable γ-phase.The fi ne multi-wave pro fi les also provide an important experimental reference for improving the phase field modeling of shock-induced phase transition.
phase transformation,elastic-plastic deformation,orientation dependence,single-crystal iron
:62.50.Ef,61.50.Ks,64.70.kd
10.7498/aps.66.146201
∗国家自然科学基金青年科学基金(批准号:11602251,11302202)和科学挑战专项(批准号:TZ2016001)资助的课题.
†通信作者.E-mail:lijun102@caep.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the Young Scientists Fund of the National Natural Science Foundation of China(Grant Nos.11602251, 11302202)and the Science Challenge Project,China(Grant No.TZ2016001).
†Corresponding author.E-mail:lijun102@caep.cn

