双机双质体振动系统的自同步运动

刘云山,张学良，闻邦椿

(1.东北大学 机械工程与自动化学院,沈阳 110819; 2.辽宁轨道交通职业学院,沈阳 110023)



双机双质体振动系统的自同步运动

刘云山1,2,张学良1，闻邦椿1

(1.东北大学 机械工程与自动化学院,沈阳 110819; 2.辽宁轨道交通职业学院,沈阳 110023)

以双机双质体振动系统为研究对象,进行了自同步运动研究.应用拉格朗日方程建立振动系统主振方向的运动微分方程,通过使用传递函数,得到了振动系统稳态时的同步响应.建立了振动系统主振方向的相对运动微分方程,得到了主振系统固有频率与振动系统稳态时相对运动的同步响应.基于以上动力学模型,对系统进行了数值仿真分析,因为亚共振有其特殊的工程意义,定量研究了振动系统在亚共振工作状态下,两电动机的转速、相位差,及两质体各自的位移与相对的位移.通过计算机的数值仿真验证了理论推导的正确性.

双机双质体振动系统; 自同步; 同步响应; 亚共振

在振动利用工程中,由振动导致的激振器同步广泛应用于各大工矿企事业中,由此也刺激更多学者对振动同步或称作自同步运动理论及应用上的探索[1-2].

依据外部运转频率与固有频率的比值(该比值以z表示),振动机械系统可分为3类:亚共振系统(z<0.95)、近共振系统(z值在1附近,0.95≤z≤1.05)以及超共振系统(z>1.05).在某些工程上,需要考虑加工成本和机器本身结构上的限制,以及亚共振或亚-近共振所特有的一些优势,要求振动机在亚共振或亚-近共振区域工作.亚-近共振的优势在于其幅-频响应有个放大因子,在所需相同振幅条件下,亚共振或亚-近共振区域内激起的振幅所需激振力是其超远共振条件下的1/5～1/3,这样如果使机器在亚共振或亚-近共振状态下工作,所需驱动电动机功率会相应降低,以此达到经济、节约的目的.因此,亚共振或亚-近共振同步运动研究有其重要意义[3-7].

本文基于推导出的双机双质体振动系统稳态时的同步运动响应,对振动系统进行了数值仿真,定量分析研究了振动机在亚共振工作状态下两质体的位移与两质体的相对位移,两电动机的转速与两电动机的相位差等内容.也验证了理论推导的正确性.

1 系统动力学模型和运动微分方程

图1为某双机双质体振动系统的力学模型,由振动质体m1和m2以及两个偏心转子m01和m02组成.振动质体水平y方向和竖直x方向分别通过弹簧与固定支架相连,两振动质体间在水平y方向通过弹簧相连.两偏心转子旋转中心o01和o02被安装在关于振动质体m2质心所在的竖直对称轴上的正上和正下方并对称布置.电动机旋转时,偏心转子产生的激振力带动振动机体振动,振动系统的水平y方向被设计为主振方向.

图1 振动系统的动力学模型

1.1 系统主振方向的运动微分方程

使用Lagrange方程并选取y1,y2,φ1,φ2为广义坐标,主振系统运动微分方程可表示为

(1)

式中:m0i为激振器i质量,i=1,2;mi为质体i质量;ky为在y方向刚度;fy为在y方向阻尼;Tei为电动机i的电磁转矩;f0i为电动机i的轴阻尼系数.

工程上,通常选择两个一样激振器,令m01=m02=m0.设两激振器平均相位及相位差分别为φ和2α,即

(2)

假设稳态时两激振器同步角速度为ωm0,由文献[8]可知,在稳态运转过程中位移和加速度关系可表示为

(3)

对式(1)前两个式子,使用传递函数法并结合式(2)和式(3),可得系统响应为

式中:

γ1y为质体m1在y方向相位滞后角;γ2y为质体m2在y方向相位滞后角.

1.2 系统主振方向相对运动微分方程

稳态时,两激振器角加速度可忽略,同时忽略f2y与k2y(因为它们相对很小,即f1y≫f2y,k1y≫k2y),有

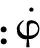
其中

式中:m为诱导质量.

由式(6),可得两质体在y方向相对运动固有频率ω0(也称为主振系统固有频率)为

(7)

式(6)的响应为

(8)

其中

阻尼系数f1y只能通过实验方法获取,工程上,对于小阻尼振动机,f1y=2ζ′1ymω0,其中ζ′1y为等效相对阻尼系数,ζ′1y≤0.07[8].

由式(8)可知,当z0=1(即ωm0=ω0)时,幅值A12在共振点处取最大值,说明ω0对应的是两质体y方向反相位相对运动固有频率.

2 系统同步运动数值仿真

实际系统参数m1=600 kg,r=0.15 m,m2=1 500 kg,f1y=3.83×103kN/(m·s-1),J01=J02=0.675 kg·m2,m01=m02=30 kg,其中m1,m2为两振动质体的质量,f1y为在两振动质体间y方向的阻尼,r为偏心转子的偏心距,m01,m02为两偏心转子的质量.可确定振动系统的结构参数为k1y=5 000×103kN/m,k2y=100×103kN/m.

在两电动机参数相同情况下,基于推导出的双机双质体振动系统稳态时的同步运动相应,并设定为亚共振工作状态,对系统进行计算仿真结果,如图2～6所示.

图2 转速曲线

图3 相位差

图4 位移y1

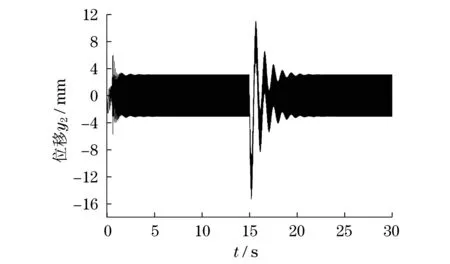
图5 位移y2

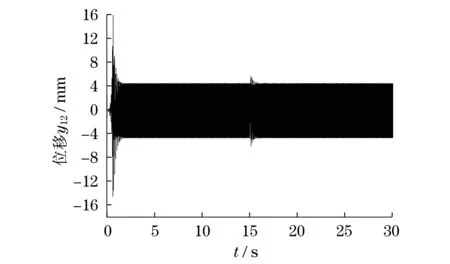
图6 位移y12

由图2可以看出,两电动机的转速从3.21 s开始稳定,大小为1 018 r/min,与电动机正常额定转速1 000 r/min很接近,几乎没有误差,在15 s加干扰后,很快在16.51 s两点电动机转速稳定转速大小仍是1 018 r/min.由图3可知,在设定的亚共振工作状态下,两电动机稳态同步的相位差为0附近,在15 s加干扰,在15.11 s相位差最大为60.45°,在18.23 s相位差重新稳定在0附近.由图4可知,振动质体m1在y方向的位移y1,振幅在开始时不太稳定,1.73 s达到最大值,最大振幅为14.15 mm,随后振幅开始减小,在6.82 s左右开始稳定,正负方向振幅大小均为1.66 mm,在15 s加干扰后,开始出现较大的不稳定,在15.78 s达到最大值,最大振幅为14.86 mm,随后开始减小,在24.51 s左右开始稳定,正负方向振幅大小仍均为1.66 mm.由图5可知,振动质体m2在y方向的位移y2,振幅在开始不太稳定,1.75 s达到最大值,最大振幅为6.11 mm,随后振幅开始减小,在3.85 s左右开始稳定,正负方向振幅大小均为3.23 mm,在15 s加干扰后,开始出现较大的不稳定,在15.63 s达到最大值,最大振幅为15.67 mm,随后开始减小,在24.44 s左右开始稳定,正负方向振幅大小仍均为3.23 mm.由图6可以看出,振动质体m1与振动质体m2在y方向的相对位移y12,振幅在开始不稳定,在1.74 s达到最大值16.26 mm.随后振幅逐渐减小,在3.16 s左右开始稳定,正负方向振幅大小均为4.83 mm,同样在15 s加干扰后,开始出现不稳定,在15.74 s达到最大值,最大振幅为6.22 mm,随后逐渐减小,在17.56 s左右开始重新稳定,正负方向振幅大小仍为4.83 mm.仿真结果与理论结果符合.

3 结论

(1) 建立双机双质体振动系统的模型,由拉格朗日方程得到振动系统微分方程,再应用传递函数得到系统的稳态振动同步响应,并建立了振动系统的相对运动微分方程,得到了固有频率与振动系统稳态时相对运动的同步响应,为之后的仿真做好了理论基础与铺垫.

(2) 定量分析了双机双质体自同步振动系统的电动机转速、两电动机相位差、两振动质体在主振方向的运动与相对运动情况,通过数值仿真模拟,验证了理论推导的正确性.

[1] WEN B C,ZHANG T X.Controlled synchronization of mechanical system[C]// Proceedings of the 3rd International Conference on Vibration and Motion Control,Tokyo,Japan.1996:327-331.

[2] ZHANG X L,ZHAO C Y,WEN B C.Theoretical and experimental study on synchronization of the two homodromy exciters in an non-resonant vibrating system[J].Shock Vib,2013,20:327-340.

[3] ZHANG X L,WEN B C,ZHAO C Y.Synchronization of three non-identical coupled exciters with the same rotating directions in a far-resonant vibrating system[J].Sound Vib,2013,332:2300-2317.

[4] ZHAO C Y,WEN B C,ZHANG X L.Synchronization of the four identical unbalanced rotors in a vibrating system of plane motion[J].Sci China Technol Sci,2010,53:405-422.

[5] ZHANG X L,WEN B C,ZHAO C Y.Vibratory synchronization and coupling dynamic characteristics of multiple unbalanced rotors on a mass-spring rigid base[J].Int J Non-Linear Mech,2014,60:1-8.

[6] ZHANG X L,KONG X X,WEN B C,et al.Numerical and experimental study on synchronization of two exciters in a nonlinear vibrating system with multiple resonant types[J].Nonlinear Dyn,2015,82:987-999.

[7] WEN B C.Synchronization theory of self-synchronous vibration machines with ellips motion Locus[C]//Proceedings of ASME Vibration and Noise Conference,Boston,America.1987:495-500.

[8] 闻邦椿,刘凤翘.振动机械的理论及应用[M].北京:机械工业出版社,1982.

WEN Bangchun,LIU Fengqiao.Theory and application of vibration machinery[M].Beijing:Machinery Industry Press,1982.

Self-synchronous motion of a dual-mass with two motors vibrating system

LIU Yunshan1,2,ZHANG Xueliang1,WEN Bangchun1

(1.School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,China;2.Guidao Jiaotong Polytechnic Institute,Shenyang 110023,China)

The self-synchronous motion of a dual-mass with two motors vibrating system is studied.The Lagrange equations were used to establish differential motion equations of the vibration system.By using the transfer function,the synchronization response of the vibration system was obtained.In addition,the relative motion differential equations of the main vibration direction of the vibration system were established.Thereby,the natural frequency of the main vibration system and the synchronous response of the relative motion of the main vibration system were approached.Based on the dynamic models,the self-synchronization simulation was performed.The vibrating system under sub-resonant working condition was quantitatively investigated,including:the two motor speed and phase difference,the displacement of the two mass and relative displacement of the two mass.And the correctness of the theoretical analysis was verified.

dual-mass with two motors vibrating system; self-synchronization; synchronous response; sub-resonance

国家自然科学基金资助项目(51375080)

刘云山(1975—),男,讲师,博士生.E-mail:liuyunshan75@163.com

TH 113

A

1672-5581(2017)02-0095-04