排列熵与核极限学习机在齿轮故障诊断中的应用

秦 波，张鲁洋，孙国栋，王建国

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

排列熵与核极限学习机在齿轮故障诊断中的应用

秦 波，张鲁洋，孙国栋，王建国

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

针对齿轮故障难提取和极限学习机（extreme learning machine，ELM）隐层节点数需要人为设定，致使齿轮故障分类模型准确度低、稳定性差的问题，提出基于核极限学习机（kernel extreme learning machine，K-ELM）的齿轮故障诊断方法。首先，将测得信号经经验模态分解（empirical mode decomposition，EMD）处理后得到一系列IMF本征模式分量，并提取各分量的排列熵（permutation entropy，PE）值组成高维特征向量集；然后利用高斯核函数的内积表达ELM输出函数，从而自适应确定隐层节点数；最后，将所得高维特征向量集作为K-ELM算法的输入建立核函数极限学习机齿轮故障分类模型，进行齿轮不同故障状态的分类辨识。实验结果表明：与SVM、ELM故障分类模型相比，核函数ELM滚动齿轮故障诊断分类模型具有更高的准确度和稳定性。

齿轮；故障诊断；排列熵；核函数；极限学习机

0 引 言

齿轮是机械系统中最关键的零部件之一，其运行状态直接关系到设备能否正常运转。由于实际工况复杂，齿轮故障振动信号常呈现出非线性、非平稳性的特征，而传统的时频域分析方法大多针对线性、稳态信号的分析，因此难以准确、稳定地识别齿轮的故障。

为了准确、稳定地识别齿轮的故障类型，国内外科研工作者提出了一系列的方法。在特征提取方面：Bandt等[1]提出采用排列熵的方法检测时间序列随机性和动力学突变行为，能够定量评估信号序列中含有的随机噪声，从而确定需要进行降噪的IMF分量。相比于其他的熵值，排列熵具有计算简单、抗噪能力强、适合在线监测等优点[2]，在脑电信号处理[3]、心率信号处理[4]等领域得到了广泛的应用。Yan等[5]将其应用于旋转机械振动信号的特征提取，并将其与近似熵和Lempel-Ziv复杂度进行了对比，能够有效地检测和放大振动信号的动态变化，并且能够表征滚动齿轮在不同状态下的工况特征。Cao等[6]利用自适应差分算法（DE）优化ELM模型的输入权重和隐层阈值，具有较好的全局搜索能力，更强的泛化能力，但收敛速度慢。Han等[7]提出PSO-ELM算法，该算法利用了改进粒子群优化算法（PSO）的良好能力优化ELM输入权重与隐层阈值，具有比E-ELM模型更强的泛化能力，但很容易陷入局部极小值而找不到全局最优解。吕忠等[8]运用遗传算法对极限学习机的输入权值与隐层阈值进行优化，从而提高模型的预测精度；但遗传算法属于随机性智能优化算法，稳定性差，不能处理连续优化问题。

针对以上问题，本文提出基于排列熵与K-ELM的齿轮故障诊断方法。为避免噪声对特征提取的影响，先将测得信号经集合经验模态分解处理后得到一系列IMF本征模式分量，并提取各分量的排列熵PE值组成高维特征向量集；其次，利用高斯核函数的内积表达ELM输出函数，从而自适应确定隐层节点数；最后，将所得高维特征向量集作为K-ELM算法的输入建立核函数极限学习机齿轮故障分类模型，进行齿轮不同故障状态的分类辨识。

1 排列熵

排列熵是通过对比相邻数据以度量时间序列的复杂性[9]。 给定一个时间序列信号{x（i），i=1，2，…，n}进行相空间重构。根据延迟嵌入定理得到重构信号：

式中y为嵌入维数。

重构后i的值最大为

将式（1）中的元素按升序排列，得到：

其中j1，j2，…，jy表示x（i）中元素的位置。 如果x（i）中存在相等的元素，则在重新排列时按j的大小进行排列，因此x（i）总能找到如下序列模式：

其中l=1，2，…，m，m≤y!。y个元素的向量最多可以有y!种排列模式；K（l）表示其中一种排列模式。设一种排列模式的出现概率为

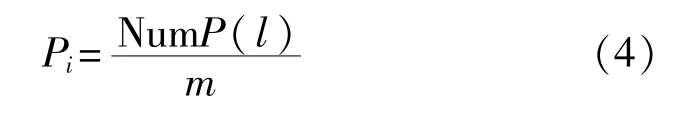
故信号排列模式的熵为

对HP=（y，σ）进行归一化处理，得排列熵为

以上可以看出，HP值的大小表示时间序列的复杂和随机程度。HP值越大，则时间序列越接近随机，反之时间序列越规则。

2 核函数极限学习机

2.1 ELM算法

极限学习机是由Huang等[10]提出的一种基于广义逆矩阵理论的新型前馈神经网络，可以一步求出输出权值，加快学习速度、提高建模效率。其结构如图1所示，由输入层、隐层和输出层组成，层与层之间通过神经元连接，n个隐层节点，ωi和βi分别为连接输入层和隐层、隐层和输出层的权重矩阵，xi、yi分别为输入和输出，bi是隐层的阈值。

算法原理如下：对于给定L个不同数据样本（xi、ti），其中xi=[xi1，xi2，…，xiL]T∈RL，ti=[ti1，ti2，…，tiL]T∈RL，具有n个隐层节点（n＜L），且激活函数为g（x）的单隐层前馈神经网络的输出表达式：

图1 ELM的结构图

如果其激活函数g（x）是无限可微的，那么就能够零误差地逼近输入样本的真实输出值，用下式可以表达为

上式可以简化为

其中H为隐层输出矩阵，定义如下：

输出权值向量βi可以通过式（9）的最小二乘βi=H+T来获得。其中H+为Moerr-Penrose广义逆矩阵，在求解H+=HT（HHT）-1时，由于测试数据存在复共线性的问题，从而造成HHT非奇异，影响最终结果。因此，Huang在对角矩阵HHT中引入一个参数1/c，把它加到HHT的主对角线上，使HHT的特征根偏离零值，以此求出权值向量βi值，表达式如下：

2.2 K-ELM算法

通过引入核函数把低维线性不可分的输入空间样本数据映射到可分的高维特征空间，进行内积运算从而将不可分转变为可分来处理数据。本文采用的高斯核函数满足Mercer核理论[11]，可以作为核函数应用到极限学习机中，其表达式如下：

在ELM的算法中，隐层节点输出函数g（x）是不知道具体形式的函数，那么就可以把g（x）的内积形式用核函数表示出来。所以核ELM算法中，隐层节点输出函数g（x）的具体形式不用给出，只需要知道核函数K（x，xi）的具体形式就可以求出输出函数的值，且隐层节点数能够自适应确定。ELM算法中的公式用核矩阵形式表示为

故核函数极限学习机算法可概括为：给定一个含有L个样本的训练样本集（xi，yi），xi表示输入向量，yi表示相应的输出，i=1，2，…，L，及核函数K（x，xi）。则输出的方程为

核极限学习机算法的流程如图2所示。

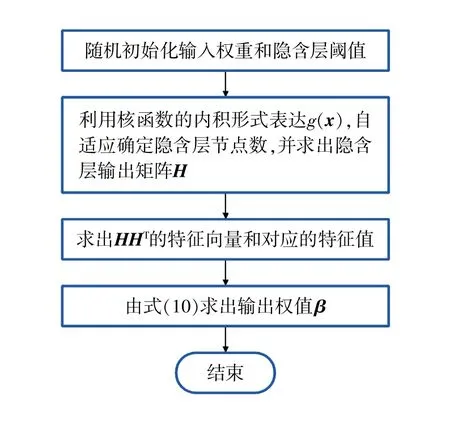
图2 核极限学习机算法的流程图

3 仿真实验

实验设备为美国Spectra Quest公司DDS动力传动故障诊断综合实验台（见图3）。该实验台的动力传动系统由1个二级行星齿轮箱，1个二级平行齿轮箱以及变速驱动电机和电机控制器等组成。实验中，测点布置见图3，位于垂直径向、水平径向与轴向所采集的振动信号经由LMS数据采集仪接入计算机进行分析、保存。

实验中，对齿轮 Z3（m=4.5；z=29）进行正常、断齿、齿根裂纹和齿面磨损4种故障件的更换，并采集上述4种状态下的振动加速度信号，采样频率为5120Hz，电机转速设为2100r/min，分别获得每种状态30组数据，每组数据包含8192个采样点。抽取每种状态20组作为训练样本，余下10组作为测试样本。首先对齿轮的正常信号进行EMD分解，对所得IMF分量提取排列熵。同理把其余3种状态的样本进行上述处理，所得结果见表1。（由于文章篇幅所限，表中只举出齿轮4种状态的前4组信号特征向量PE值）

图3 动力传动故障诊断综合实验台

为验证上述方法的优越性。分别将表1中的特征向量输入到SVM、ELM与K-ELM中进行训练与测试，其中SVM中惩罚参数C与核宽度系数σ设为2与0.2；3种算法的测试样本分类结果分别如图4～图6所示。从图4中看出SVM对于轴承故障分类正确率达到90%（36/40）；从图5中看出ELM对于轴承故障分类正确率达到95%（38/40）；从图6中看出，K-ELM对于轴承故障分类正确率达到100%（40/40）。上述3种方法的对比结果如表2所示。

表1 齿轮4种状态的特征向量

图4 SVM的测试样本分类结果

图5 ELM的测试样本分类结果

4 结束语

针对齿轮故障信号特征难提取和极限学习机隐层节点数需要人为设定，致使齿轮故障分类模型准确度低、稳定性差的问题，本文提出基于K-ELM的齿轮故障诊断方法。将提取的各IMF分量的排列熵作为本模型的输入，进行齿轮故障的分类和识别。通过实验结果分析，得出如下结论：

1）排列熵对信号的突变特别敏感，对于齿轮不同振动信号的复杂性不同，排列熵值也不同，因此排列熵用来提取故障特征效果明显。

2）核函数极限学习机的隐层节点数能自适应确定。齿轮故障诊断模型的分类准确度和稳定性得以提高，在齿轮故障诊断领域有广泛的应用前景。

图6 K-ELM的测试样本分类结果

表2 SVM、ELM、K-ELM 3种诊断模型性能比较

[1]BANDT C， POMPE B.Permutation entropy： a natural complexity measure for time series[J].Physical Review Letters the American Physiological Society，2002，88（17）：174102.

[2]周涛涛，朱显明，彭伟才，等.基于CEEMD和排列熵的故障数据小波阈值降噪方法[J].振动与冲击，2015，34（23）：207-211.

[3]姚文坡，刘铁兵，戴加飞.脑电信号的多尺度排列熵分析[J].物理学报，2014，63（7）：078704.

[4]马千里，卞春华.改进排列熵方法及其在心率变异复杂度分析中的应用[J].中国组织工程研究与临床康复，2010，52（140）：9781-9785.

[5]YAN R Q， LIU Y B， GAO X.Permutation entropy： a nonlinear statistical measure for status characterization of rotary machines[J].MechanicalSystemsand Signal Processing，2012，29（5）：474-484.

[6]CAO J W， LIN Z P，HUANG G B.Self-adaptive evolutionary extreme learning machine [J].Neural Processing Letters，2012，36（3）：285-305.

[7]HAN F， YAO H F， LING Q H.An improved evolutionary extreme learning machine based on particle swarm optimization[J].Neurocomputing，2013（116）：87-93.

[8]吕忠，周强，周棍，等.基于遗传算法改进极限学习机的变压器故障诊断[J].高压电器，2015，15（8）：49-53.

[9]郑近德，程军圣，杨宇，等.多尺度排列熵及其在滚动轴承故障诊断中的应用 [J].中国机械工程，2013，24（19）：2641-2646.

[10]苑津莎，张利伟，王瑜.基于极限学习机的变压器故障诊断方法研究[J].电测与仪表，2013，50（12）：21-26.

[11]张晓平，赵玛，王伟，等.基于最小二乘支持向量机的焦炉煤气柜位预测模型及应用 [J].控制与决策，2010，25（8）：1178-1183.

（编辑：莫婕）

Application of permutation entropy and kernel extreme learning machine in fault diagnosis of gear

QIN Bo， ZHANG Luyang， SUN Guodong， WANG Jianguo
（School of Mechanical Engineering，Inner Mongolia University of Science&Technology，Baotou 014010，China）

Due to the low accuracy and poor stability of gear fault classification model because of the hard extraction of gear fault and artificial settings for the number of hidden layer nodes of extreme learning machine（ELM）， a gear fault diagnosis method based on kernel extreme learning machine（K-ELM） is proposed.First， a series of IMF intrinsic mode component can be obtained after empirical mode decomposition（EMD） for measured signal， and permutation entropy value（PE） of various components should be extracted to form a vector set with high-dimension features.Second，the inner product of Gauss kernel function should be used to express the ELM output function to adaptively determine the number of the hidden layer nodes.After that，the high dimension feature vector set is used as the input of the K-ELM algorithm to establish the kernel function extreme learning machine gear fault classification model to achieve the classification and identification under different fault states of gears.The experimental results show that the K-ELM gear fault diagnosis classification model has higher accuracy and stability by comparing with the fault classification model of SVM and ELM.

gear； fault diagnosis；permutation entropy；kernel function；extreme learning machine

A

：1674-5124（2017）07-0108-04

10.11857/j.issn.1674-5124.2017.07.021

2016-10-10；

：2016-12-12

国家自然科学基金（51565046）；内蒙古自然科学基金（2015MS0512）；内蒙古科技大学创新基金（2015QDL12）

秦 波（1980-），男，河南南阳市人，讲师，硕士，研究方向为复杂工业过程建模、优化及故障诊断。