改进FMECA的工业机器人失效风险分析

陈锦汉，余荣斌

（广东产品质量监督检验研究院，广东 广州 510330）

改进FMECA的工业机器人失效风险分析

陈锦汉，余荣斌

（广东产品质量监督检验研究院，广东 广州 510330）

针对传统失效模式、影响及危害性分析（FMECA）方法利用风险优先数（RPN）对失效风险进行量化排序存在RPN量化取值不连续，指标自身无明确物理意义、受主观影响较大，指标设计未考虑权重因子等缺陷，该文提出一种基于风险度量和风险排序的改进FMECA模糊综合评判法，设计重复偏差率P、维修费用W和发生概率O的全新评估指标集，利用模糊综合评判，引入层次分析法进行权重赋值。结果表明：该方法可以有效改善FMECA方法量化排序不合理、重复现象，实现指标评价的客观化、意义化和风险评价指标的量化连续性、权重化，提高工业机器人失效风险分析结果可信性。

改进FMECA；工业机器人；失效风险分析；模糊综合评判

0 引 言

工业机器人已逐步在各国制造领域得到广泛应用，成为衡量一个国家制造业水平和科技水平的重要标志[1-2]。由于工业机器人集光机电算于一体、结构精密，且工作环境复杂、工作自由度较高，一旦发生严重故障，可能造成难以预测的后果。因此有必要开展工业机器人可靠性的评估研究，其中失效风险分析是开展该研究的前提和基础[3-4]。

目前主要失效分析方法有失效模式、影响及危害分析（failure mode，effect and criticality analysis，FMECA）、故障树（failure tree analysis，FTA）、跳动式分析（bouncing failure analysis，BFA）等，其中 FMECA是一种常用系统失效分析方法[5-6]。FMECA通常采用RPN法（因素集为严重程度S、发生频度O和探测度D）进行分类取值，分析产品中所有可能产生的失效状况对产品、系统造成的影响。该方法虽然易于操作，但应用到工业机器人失效判别上存在失效风险指标不连续、失效风险排序主观影响较大等问题[7-10]。

本文针对传统FMECA方法在工业机器人失效风险分析存在的问题，提出一种基于全新评估指标集的改进FMECA失效风险分析方法。该方法实现了指标评价的客观化、意义化；构建模糊因素评判矩阵，利用层次分析法进行权重赋值，实现风险评价指标的量化连续性、权重化；并应用于工业机器人失效风险分析，有效改善FMECA方法量化排序不合理、重复现象，使分析与实际更加切合，提高工业机器人失效风险分析结果可信性。

1 基于改进FMECA的工业机器人失效风险评判方法

图1为基于改进FMECA的工业机器人失效风险评判方法流程图。

为解决RPN值指标体系存在的问题，需建立一套客观可信的评价指标体系。结合工业机器人经验数据及生产工艺情况，建立全新评价PWO指标因素集替代RPN值指标体系（见表1）。

1.2 构建影响因素评判矩阵及其权重

利用专家评价法构建影响因素评判矩阵，每位专家对失效部件k影响因素做出评价等级νj，若s位成员中评定隶属于νj的有人，则得到的评价集：

图1 基于改进FMECA失效风险评判法流程图

为了体现各影响因素重要程度，可通过引入权重集赋予相应因素加权因子。加权因子的恰当与否，将直接影响综合评判结果。

常用的权重赋值方法有德尔菲法（专家意见法）、熵值法、层次分析法AHP等[11]。其中层次分析法AHP具有定性、定量分析相结合特点，利用一致性检验，能够尽量消除人为因素，保证权重的有效性、实用性，是目前广泛应用的一种赋权方法[12]。其步骤如下：

第一，在摆放图书的过程中，最好正面朝外。为了方便幼儿查阅，以及通过有趣的图案吸引幼儿，应该要求图书的正面朝外。在兴趣的激发下，幼儿才愿意去探究图书内有趣的故事内容[1]。比如，在《大脚丫跳芭蕾》的绘本中，幼儿肯定忘不了封面那个舞姿优美的女孩以及她那双夸张的大脚，通过强烈的对比会激发幼儿的兴趣，让他们了解到贝琳达坚持梦想的励志故事。

表1 工业机器人影响因素的评价指标体系1）

1）利用1-9标度法[13]进行比较取值，建立两两比较判别矩阵如下：

式中pij为两两比较取值，可以看出，判别矩阵中pii=1，pij=1/pji。根据判别矩阵，求出最大特征根所对应的特征向量，该向量即为所求权重。

2）为了降低定性分析的人为因素影响，可对判别矩阵进行一致性检验。一致性检验公式为

式中λmax为矩阵最大特征根。IR为平均随机一致性指标，其取值见表2。若Rc＜0.1，则判断矩阵的一致性结果满意。

1.3 进行综合风险评判

设所求失效部件k的权重因素集为Wk=[w1k，w2k，…，wnk]，则模糊综合评判集为

为了更直观看出评判结果，将模糊综合评判向量进行加权平均处理，得出综合风险评价因子Ck：

2 实例应用

本实例以目前工业机器人中应用最广的机械手臂为分析对象，首先利用传统FMECA方法进行失效风险分析，结果如表3所示。

表2 1-9阶判别矩阵取值表[13]

可以看出，故障部件5排在风险评估最小位置，故障部件2、3排序重复，排序结果明显与实际情况不符。利用改进FMECA模糊综合评判法对上述机械手臂实例进行失效风险分析。

2.1 确定评价因素集

如前所述，选取因素集U={重复偏差率P、维修费用W、发生概率O}，各影响因素评价指标取值按表1进行。

2.2 构建评判矩阵及权重赋值

以电连接器断裂或烧毁（故障部件1）为例，利用德尔菲法评定法，该故障的重复偏差率P模糊集为R11={0.6，0.4，0.0，0.0，0.0}、 维修费用W模糊集为R21={0.0，0.0，0.2，0.7，0.1}、发生概率O模糊集为R31={0.0，0.0，0.4，0.6，0.0}，因此该故障模式模糊评判矩阵为

根据1-9标度法，构造该故障的两两判别矩阵并计算权重集（见表4）。

计算一致性检验判定值Rc=0.055 9＜0.1，说明该评判矩阵一致性满足要求，因此该故障的权重集为W1=[0.0810，0.1884，0.7306]。

表3 基于FMECA的工业机械手臂失效风险分析

表4 各影响因素判别矩阵及权重

2.3 进行综合风险评判

根据式（6），故障部件1的综合判定集为

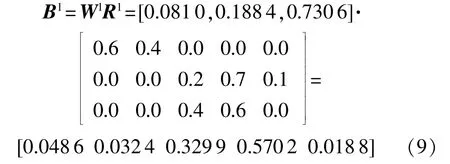
将模糊综合判定集进行加权平均处理，得出综合风险评价因子C1=2.0491。同样方法可以得出故障部件2～5的模糊因素评判矩阵：

为简便计算，各故障部件采用同一权重集，即：

从而可求出各故障部件模糊综合判定集为

同理，得出各故障部件的综合风险评价因子集：

根据表3传统RPN值排序结果，明显与实际情况不符。利用本文方法得到的综合风险评价因子排序结果为：故障部件5＞故障部件3＞故障部件2＞故障部件1＞故障部件4，其中故障部件5同步带磨损断裂导致风险排序最大，排序重复问题也得到解决，这与实际情况是相符合的。

3 结束语

本文指出传统FMECA方法在工业机器人失效风险判别存在问题，提出一种基于风险度量和风险排序的改进FMECA模糊综合评判法，较好解决了传统分析方法存在的主观性较强、指标意义不明确等问题。应用结果表明，本方法能有效改善传统FMECA方法风险排序不合理、重复现象，使分析与实际更加切合，得到评判结果更具可信性，为进一步开展工业机器人可靠性评估和维修决策的制定提供技术支持。

[1]王田苗，陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报，2014，50（9）：1-13.

[2]任志刚.工业机器人的发展现状及发展趋势[J].装备制造技术，2015（3）：166-168.

[3]BROGARDH T.Present and future robot control development-An industrial perspective[J].Annual Reviews in Control，2007，31（1）：69-79.

[4]李彤，贾庆轩，陈钢，等.面向轨迹跟踪任务的机器人运动可靠性评估[J].系统工程与电子技术，2014，36（12）：2556-2561.

[5]LIU H C， LIU L， LIU N.Risk evaluation approaches in failure mode and effects analysis：A literature review[J].Expert Systems with Applications，2014，40（2）：828-838.

[6]黄健宇.论FMEA的分析与应用[J].机械工业标准化与质量，2007（4）：37-41.

[7]毛月秋.项目风险度量、排序和评价方法的研究评述[J].西南农业大学学报（社会科学版），2014，9（6）：42-43.

[8]向鹏成，赵艳玲，王林.项目风险的多维描述与度量[J].重庆大学学报（自然科学版），2011（4）：148-152.

[9]斯泰蒙迪斯.故障模式影响分析FMEA从理论到实践[M].陈晓彤，姚绍华，译.北京：国防工业出版社，2010：46-47.

[10]DEWI D S， SYAIRUDIN B， NIKMAH E N.Risk management in new product development process for fashion industry：case study in hijab industry[J].Procedia Manufacturing，2015,4：383-391.

[11]姚立真.可靠性物理[M].北京：电子工业出版社，2004：69-70.

[12]LI W，SHANG Y M，JI Y J.Analysis of multiple objective decision methods based on entropy weight[J].ComputationalIntelligence and IndustrialApplication，2008，1（12）：953-956.

[13]骆正清，杨善林.层次分析法中几种标度的比较[J].系统工程理论与实践，2004，24（9）：51-60.

（编辑：商丹丹）

Failure risk analysis for industrial robot based on improved FMECA

CHEN Jinhan，YU Rongbin
（Guangdong Testing Institute of Product Quality Supervision，Guangzhou 510330，China）

Aiming at the defect such as discontinuous quantitative of risk priority number（RPN）of quantitatively ordination，no clear physical meaning of index itself，large subjective influence，no weighting factor considered for index design of traditional failure mode，effects and criticality analysis（FMECA），a new method of improved FMECA fuzzy comprehensive evaluation based on risk measurement and risk ranking is presented，which is used to evaluate brand new assessment index set of designing repeatability error rateP，maintenance costWand probabilityO，using the fuzzy comprehensive evaluation to judge，and analytic hierarchy process is introduced for weight assignment.Resultsshow thatthemethod can effectively improve theunreasonable FMECA quantitatively ordination and repetition，which achieves objective and significantindex evaluation and quantitative continuity and the weight of risk evaluation index，and improves the credibility of failure risk analysis results of industrial robot.

improved FMECA；industrial robot；failure risk analysis；fuzzy comprehensive evaluation

A

：1674-5124（2017）07-0016-04

10.11857/j.issn.1674-5124.2017.07.003

2017-03-21；

：2017-04-19

国家质量监督检验检疫总局资助项目（2016QK025）

陈锦汉（1960-），男，江西高安市人，高级工程师，主要从事检验检测技术研究及管理工作。