基于改进预测校正的滑翔飞行器再入制导方法

施健峰 刘运鹏 梁禄扬

北京航天自动控制研究所,北京100854



基于改进预测校正的滑翔飞行器再入制导方法

施健峰 刘运鹏 梁禄扬

北京航天自动控制研究所,北京100854

针对高超声速滑翔飞行器滑翔再入制导问题，提出了一种基于高度变化率反馈的改进倾侧角校正方法。在不依赖准平衡滑翔条件下，该方法可以得到较为平滑的弹道。纵向制导采用落点误差预测校正倾侧角指令，同时以终端平衡滑翔倾侧角作为终端倾侧角，可以提高终端高程精度。横侧向制导设计了航向角误差走廊边界控制倾侧角反转，以保证制导精度。仿真结果表明，该算法制导指令解算时间小于1s，制导精度较高。 关键词 滑翔飞行器；轨迹规划；预测校正；倾侧角校正

高超声速滑翔飞行器兼有航空器和航天器的优点，它采用升力体气动外形，具有较强的大气层内机动能力，可以完成物资运输或远程打击任务，是未来飞行器的一个重要发展方向，也是目前的一大研究热点。

再入制导技术是高超声速飞行器关键技术之一，一般分为2大类[1]：1)跟踪预先设计好的标称轨迹制导[2]，它具有计算量小，易于实现等优点，但也存在落点精度低，易受扰动影响等不足；2)利用预测能力对落点进行预测，并实时校正控制量的预测校正制导[3]。由于预测校正法是对飞行器的飞行状态进行实时分析，因而对初始散布误差以及再入过程气动偏差具有较强的鲁棒性，制导精度也比标称轨迹制导高，目前正成为再入制导技术的发展趋势。

国内外学者对预测制导算法进行了广泛深入的研究，取得了大量研究成果。Masciarelli[4]提出一种基于阻力加速度和高度变化率误差反馈的混合预测制导律，通过预测弹道误差并调整倾侧角提高落点精度；周军[5]提出一种基于高斯伪谱法的再入分段预测校正制导方法；王青[6-7]等以能量为自变量建立三自由度运动学方程，基于剩余航程随能量单调变化的特性对标准轨迹进行分段，分别进行在线校正预测制导，减少了制导指令解算时间并提高了制导精度；Lu P[8]在准平衡滑翔条件下，设计了一种简单高效的预测校正制导方法，将再入滑翔飞行中的过程约束转化为倾侧角的边界约束，通过数值积分预测飞行器的待飞航程误差，实时校正倾侧角控制指令。在此基础上，唐硕[9]、周浩[10]等提出了分段预测校正制导方法，进一步提高了落点预测精度和迭代计算效率。

本文在上述文献基础上，针对传统预测校正制导轨迹周期性震荡以及终端精度鲁棒性较差的问题，对方法进行改进，提出一种能够有效抑制周期性轨迹震荡的滑翔制导律，提高了制导精度。

1 问题描述

1.1 三自由度再入运动方程

考虑地球自转影响的高超声速飞行器三自由度无量纲动力学方程为：

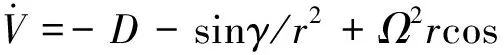
(sinγcosφ-cosγsinφcosψ)

Ω2rcosφ·(cosγcosφ+sinγcosψsinφ)]/V

2ΩV(tanγcosψcosφ-sinφ)+

Ω2rsinψsinφcosφ/cosγ]/V

(1)

式中，r为飞行器质心距地心的径向距离；V为飞行器相对于地球固连坐标系的速度；θ和φ分别为飞行器所处的经度和纬度；γ和ψ分别为航迹倾角与

航迹偏角；σ为倾侧角；Ω为地球自转角速度；L和D分别为无量纲的升力加速度和阻力加速度，具体计算公式为

L=0.5R0SrefρV2CL/m

D=0.5R0SrefρV2CD/m

(2)

式中，R0为地球半径，Sref为飞行器的参考面积，m为飞行器质量；CL和CD分别为升力系数和阻力系数；ρ为大气密度。

1.2 再入过程约束

飞行器在再入过程中面临严重的气动受热、动压及过载问题，即受到动压约束、过载约束和气动加热约束。具体计算公式为：

Q=KQρ0.5V3.15≤Qmax

q=0.5ρV2R0g0≤qmax

(3)

式中，Qmax，qmax和nmax分别为飞行器所能承受的热流密度、动压和过载的最大幅值；KQ为与飞行器相关的常值参数，由高超声速飞行器自身的材料和外形决定，本文仿真算例选取KQ=2.8135×10-4；g0为海平面的地球引力加速度。

1.3 再入末端约束

再入轨迹的末端约束随具体问题变化，本文考虑的再入飞行末端约束主要包括末端高度约束、末端速度及末端经度与纬度约束。不失一般性，定义如下能量形式的无量纲变量e：e=1/r-V2/2，末端约束可以表示为

r(ef)=rf

V(ef)=Vf

θ(ef)=θf

φ(ef)=φf

(4)

式中，rf和Vf分别为给定末端高度和末端速度。

2 预测校正制导

2.1 纵向制导律设计

确定再入飞行器质心运动的控制量是攻角α和倾侧角σ。再入飞行器初始下降段气动加热最为严重，此时采用大攻角飞行，可减小气动加热；当飞行速度热流密度不是主要制约因素时，采用大升阻比攻角飞行，以满足航程要求。通常纵向制导攻角采用如下的分段函数：

α(V)=

(5)

式中，αmax为初始下降攻角，V1α,V2α分别为分段点速度。

纵向倾侧角剖面的设计主要是为了满足再入航程要求。高超声速飞行器由于再入高度较高，大气密度小而导致气动力较小，初始下降段飞行器采用常值倾侧角飞行的开环制导方式，而不对航程进行预测。

(6)

式中，σ0为待搜索参数，σf为预定值。在每个制导周期内，给定初始倾侧角幅值，可以通过对纵向轨迹进行积分，得到其剩余飞行能力，通过割线法调节σ0实现射程的满足。

定义终端时刻待飞航程偏差为：

(7)

式中，待飞航程stogo(ef)取为星下点的圆弧长度，

stogo(ef)=arccos[sinφsinφf+

cosφcosφfcos(θf-θ)]

(8)

定义s为待飞航程，忽略地球自转，以无量纲能量e为自变量的纵向运动方程为：

ds/de=-cosγ/rD

dr/de=sinγ/D

dγ/de=[Lcosσ+(V2-1/r)cosγ/r]/DV2

(9)

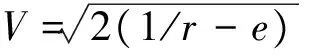
(10)

式(6)～(10)给出了满足航程约束的经典预测制导方法，由于该方法不依赖准平衡滑翔条件(QEGC)，其规划出的轨迹通常是震荡的。同时，该方法只对航程进行了反馈控制，一般不能保证终端高度的精度。因此，本文在传统预测制导方法基础上进行了改进。

首先，在倾侧角指令中增加高度变化率反馈，使升力在负重力方向的分量更快地平衡重力，从而抑制再入滑翔过程中产生的高度震荡。计算公式为：

(11)

k=

(12)

式中，k0,V1k,V2k根据初始状态与终端约束条件而定。

综上，预测校正算法在每个制导周期内纵向制导量的计算流程如图1所示。

图1 纵向制导计算流程

理论分析与数学仿真发现，飞行器终端高度与终端倾侧角σf相关性很大。采用高度变化率反馈之后，飞行器在滑翔中后段可以认为处于准平衡滑翔状态，因此，在滑翔终端， 倾侧角σf的选取为终端高度、速度条件下的准平衡滑翔倾侧角，即满足：

(13)

式中，rf，Vf，Ω分别为给定末端高度、末端速度和地球自转角速度。

滑翔飞行器再入应满足过程约束，本文将热流密度约束、动压约束和过载约束进行转化，在高度-速度平面建立飞行器控制倾侧角的幅值约束，表达式为：

(14)

再入滑翔过程中最大倾侧角为：

(15)

2.2 侧向制导律设计

侧向制导的主要任务是设计倾侧角反转逻辑，使飞行器能到达指定区域。本文采用设计航向角误差走廊的方式实现侧向控制。定义Ψ为飞行器当前位置视线方位角，计算如下：

(16)

当前航向误差角为δψ=ψ-Ψ。倾侧角反转逻辑为：当航向角误差δψ超出误差走廊的上边界时，倾侧角指令为负；当航向角误差δψ超出走廊的下边界时，倾侧角指令为正；当航向角误差δψ位于误差走廊内时，倾侧角符号保持不变。

sgn(σi)=

(17)

其中，误差门限设计为速度的分段线性函数，表达式如下：

ψup=-ψdown

(18)

V1,V2根据精度需求可以通过仿真计算得到。

3 仿真分析

选取高超声速再入飞行器CAV-H为仿真对象，主要特征参数为:飞行器质量为907.2kg，气动参考面积为0.4839m2，最大升阻比约为3.5；过程约束为：热流密度约束为3.0MW/m2，动压约束为300kPa，最大过载约束为5.0g。飞行器初始飞行状态与终端飞行约束如表1所示。标称攻角剖面为：αmax=25°，αmaxL/D=10.5°，V1α=16Ma，V2α=11Ma。倾侧角指令的取值范围为:-80°≤σ≤80°，倾侧角反馈控制增益系数剖面为：k0=20，V1k=Vf+2000(m/s)，V2k=V0-1500(m/s)。预测校正周期为50s。

表1 飞行器初始再入状态与终端约束

为验证本文算法的有效性，将本文算法与传统预测校正方法进行了对比仿真，结果如图2～7所示。

图2 高度变化曲线

图3 弹下点位置曲线

图4 倾侧角曲线

图5 热流密度曲线

图6 过载曲线

图7 动压曲线

通过对比，得到以下结论：

1)与标准轨迹制导相比，预测校正制导具有很大的灵活性，具备一定的在线轨迹规划能力；仿真结果表明落点经纬度误差不超过0.05°，制导精度较高；

2)热流密度、动压和过载约束均未超过给定的最大值限度，相比传统预测校正制导方法，本文的弹道、热流密度、过载和动压克服了周期性震荡，曲线光滑，有利于飞行器热/压防护。理论上通过添加准平衡滑翔条件(QEGC)也可以抑制轨迹震荡，但QEGC只能限制高度震荡的上边界，在航迹角增大时可能失效，本文通过增加高度阻尼抑制震荡，更具普适性。

4 结论

针对高超声速飞行器滑翔再入制导问题，在传统预测校正制导的基础上进行了改进。针对传统预测校正弹道容易震荡的问题，通过在倾侧角指令中引入高度变化率反馈，增加了制导系统的阻尼，有效抑制了弹道震荡。传统预测校正方法高程精度一般无法保证，本文通过分析与仿真验证了在终端倾侧角满足准平衡滑翔条件下，高程精度可以提高。侧向制导设计了基于航向误差角走廊的倾侧角反转逻辑，保证了位置精度。仿真分析表明本文方法制导精度高，指令解算快。后续将开展扰动条件下的预测制导研究，为工程应用奠定基础。

[1] 赵汉元．飞行器再入动力学和制导[M]．长沙:国防科学技术大学出版社，1997:7-22.

[2] Dukeman G A．Profile-following Entry Guidance Using Linear Quadratic Regulator Theory[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit．Monterey: AIAA，2002，4457:1-10.

[3] Joshi A，Sivan K．Predictor Corrector Reentry Guidance Algorithm with Path Constraints for Atmospheric Entry Vehicles[J]．Journal of Guidance Control and Dynamics，2007，30(5):1307-1318.

[4] Masciarelli J P，Westhelle C，Grave C．Aero Capture Guidance Performance for the Neptune Orbiter[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit．Rhode Island: AIAA，2004，4954:1-7.

[5] 水尊师，周军，葛致磊．基于高斯伪谱方法的再入飞行器预测校正制导方法研究[J]．宇航学报，2011，32(6):1249-1255.(Shui Zunshi，Zhou Jun，Ge Zhilei．On-line Predictor-corrector Reentry Guidance Law Based on Gauss Pseudo Spectral Method[J]．Journal of Astronautics，2011，32(6):1249-1255.)

[6] 王青，冉茂鹏，赵洋．基于预测校正法的高超声速飞行器再入制导[J]．北京航空航天大学学报，2013，39(12):1564-1568.(Wang Qing，Ran Maopeng，Zhao Yang．Reentry Guidance for Hypersonic Vehicle Based on Predictor-corrector Method[J]．Journal of Beijing University of Aeronautics and Astronautics，2013，39(12):1564-1568．)

[7] 王青，莫华东，吴振东，等．基于能量的高超声速飞行器再入混合制导方法[J]．北京航空航天大学学报，2014，40(5):580-585.(Wang Qing，Mo Hua dong，Wu Zhengdong，et al．Energy-based Hybrid Reentry Guidance for Hypersonic Vehicles[J]．Journal of Beijing University of Aeronautics and Astronautics，2014，40(5):580-585．)

[8] Xue S，Lu P．Constrained Predictor-corrector Entry Guidance[J]．Journal of Guidance Control and Dynamics，2010，33(4):1273-1281．

[9] 王智，唐硕，闫晓东．高超声速滑翔飞行器约束预测校正再入制导[J]．飞行力学，2012，30(2):175-180．(Wang Zhi，Tang Shuo，Yan Xiaodong．Constrained Predictor-corrector Reentry Guidance for Hypersonic Glide Vehicle[J]．Flight Dynamics，2012，30(2):175-180.)

[10] 刘冠南，周浩，陈万春．高超声速飞行器再入多段导引方法研究[J]．飞行力学，2012，30(4):337-341．(Liu Guannan，Zhou Hao，Chen Wanchun．A Study on the Multiple Phrase Reentry Guidance Method of Hypersonic vehicle[J]．Flight Dynamics，2012，30(4):337-341.)

Gliding Vehicle Reentry Guidance Based on Improved Predictor-Corrector

Shi Jianfeng， Liu Yunpeng， Liang Luyang

Beijing Aerospace Automatic Control Institute，Beijing 100854，China

Regardingthereentrytrajectoryguidanceprobleminhypersonicglidevehicle,animprovedpredictor-correctorguidancemethodbasedonthefeedbackofthealtitudechangerateisproposed.Smoothtrajectorycanbegeneratedbyapplyingthismethodwhichisindependentofthequasiequilibriumglidecondition(QEGC).Thelongitudinalguidanceisdevelopedbypredictingthelongitudinalrangeerrorandcorrectingthemagnitudeofthebankanglecommand,meanwhile.ThispaperpresentsthatitcanimprovetheheightprecisioniftheterminalbankanglemeetstheQEGC.Alateralreversallogicbasedontheheadingangleerrorcorridorisdesignedforlateralguidance．Thesimulationresultsshowthattheproposedmethodgeneratestheguidancecommandsinlessthan1secondandhashighguidanceprecision.

Glidingvehicle;Trajectoryplanning;Predictor-corrector;Bankanglecorrect

2016-11-30

施健峰(1988-)，男，浙江义乌人，博士研究生，主要研究方向为导航、制导与控制；刘运鹏(1986-)，男，江西赣州人，工程师，主要研究方向为导航制导与控制；梁禄扬(1987-)，男，四川隆昌人，工程师，主要研究方向为导航、制导与控制。

V448.232

A

1006-3242(2017)02-0051-05