利用时差/频差联合算法提高四星定位精度研究

曾博韬 陆浩然 郭贤生 郭业波 刘 洋

1.电子科技大学，成都611731 2.北京宇航系统工程研究所，北京100076



利用时差/频差联合算法提高四星定位精度研究

曾博韬1陆浩然2郭贤生1郭业波1刘 洋1

1.电子科技大学，成都611731 2.北京宇航系统工程研究所，北京100076

为了有效提高四星空间定位精度和四星定位系统在工程上的可实现性，在四星时差(TDOA)定位算法的基础上，引入频差信息，用时差/频差(TDOA/FDOA)联合定位算法对四星定位的几何精度因子(GDOP)进行优化。仿真结果表明:与TDOA定位相比，绝对位置测量精度对TDOA/FDOA定位精度的影响很小；且在相同参数条件下，针对菱形构型，四星TDOA/FDOA联合定位拥有更好的精度和更均匀的GDOP分布；四星TDOA/FDOA联合定位精度优于四星TDOA的定位精度。 关键词 四星定位；TDOA/FDOA；GDOP；星座构型

随着航天技术的日益发展,基于小卫星平台的高精度无源定位,在民用和军事领域都有着重要作用和广泛的应用前景[1]。通过增加目标的测量信息、采用联合定位的方式来提高定位精度、增大侦察范围是航天电子侦察技术的发展趋势[2]。近年来,国内外有关单位开展了双星TDOA/FDOA联合定位方法研究,为TDOA/FDOA联合定位体制研究奠定了基础[3-5]。也有相关文献对多星TDOA/FDOA联合定位进行了研究[6-9]。本文针对四星TDOA/FDOA联合定位方法的定位性能展开研究,与TDOA定位体制相比,着重反映了其在菱形构形及受绝对位置测量精度影响方面的优越性。

1 四星TDOA定位算法原理

假定三维时差定位系统的模型(图1所示)由1颗主星和3颗副星构成，S0为主星，S1,S2,S3为副星，坐标分别为Si(xi,yi,zi)，其中i=0,1,2,3。待求解的目标辐射源位置为p(x,y,z)。

图1 四星时差定位几何示意图

由各个卫星、目标辐射源的位置及辐射源与各卫星之间的距离，可得：

Δri=ri-r0，

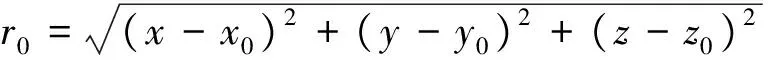
(1)

其中，ri表示第i颗副星与目标辐射源之间的径向距离，Δri表示目标辐射源和第i颗副星之间的径向距离(其中i=1,2,3)和其与主星之间径向距离的差值。简化、整理上述方程组可得：

(x0-xi)x+(y0-yi)y+(z0-zi)z=r0Δri+ki

(2)

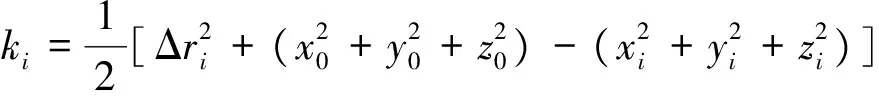
Ax=f

(3)

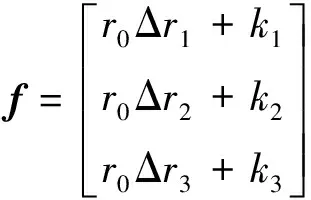
卫星位置理想的情况下，rank(A)=3，使用伪逆求解方程可得：

x=(ATA)-1ATf

(4)

下面进行四星TDOA定位算法的精度分析。对距离差Δri求微分，可得：

d(Δri)=(cix-c0x)dx+(ciy-c0y)dy+

(ciz-c0z)dz-cixdxi-ciydyi-cizdzi+c0xdx0+

coydy0+c0zdz0

(5)

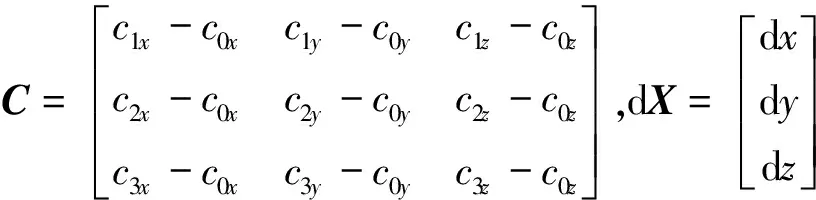
则有：

C·dX=dY-U0dS0+U1dS1+U2dS2+U3dS3

(6)

令B=(CTC)-1CT，由于主星对辐射源信号到达时间的测量存在误差，且误差存在于每个时间差的测量中，所以每个Δri的测量误差都是相关的。假设通过系统修正后测量误差的均值为0，而且卫星位置误差的每个元素之间以及各卫星位置误差之间不相关，则目标辐射源定位误差的协方差矩阵为：

(7)

式中，E[dY·dYT]=

(8)

目标辐射源的位置误差协方差矩阵为：

(9)

依据GDOP的定义获得三维空间时差系统定位的几何稀释精度：

(10)

2 四星TDOA/FDOA联合定位算法原理

在四星TDOA定位算法基础上，四星TDOA/FDOA联合定位算法加入了频差信息，目标辐射源的坐标位置记为p(x,y,z)，主星坐标位置记为S0(x0,y0,z0)，速度记为v0(vx0,vy0,vz0)，副星坐标位置记为Si(xi,yi,zi)，速度记为vi(vxi,vyi,vzi),其中i=1,2,3，则由目标辐射源到达主副星的时间差以及频率差为：

(11)

(12)

式中，i=1,2,3；j=4,5,6；tdoai为到达时间差，fdoai为到达频率差；f为辐射源辐射频率；c为光速。通过求解方程的最小二乘解，得到目标位置。本文旨在分析四星定位精度，故定位方程的求解过程不再进行赘述。

对上述式中的tdoai,fdoai，(x,y,z)，(xi,yi,zi)，vi(vxi,vyi,vzi)进行一阶线性近似展开，可得：

(13)

将上式记为：

(14)

(15)

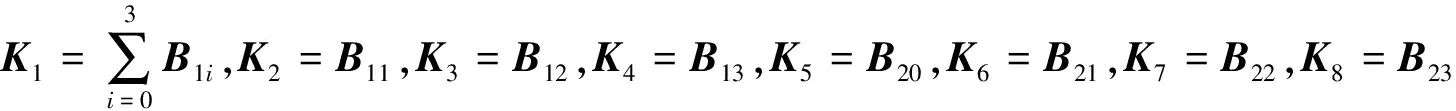
(16)

式中，M为TDOA和FDOA测量精度的相关矩阵；Ei为位置测量精度和速度测量精度的相关矩阵。

定位精度可用式(17)计算出的3个正交方向的测量精度σx,σy,σz表示，即

(17)

由上面的分析结果可以看出，计算定位精度要用到M，Ei，即要计算TDOA和FDOA测量精度相关矩阵、位置测量精度及速度测量精度相关矩阵。

3 仿真分析

假设卫星轨道高度200km，基线长度60km，四星分别采用Y构型、T构形和菱形构形，时差测量精度50ns，频差测量精度10Hz，速度测量精度1m/s，卫星绝对位置测量精度150m，卫星相对位置测量精度50m，仿真分别得到TDOA定位和TDOA/FDOA联合定位的GDOP分布如图2～4所示。

图2 Y构型下TDOA定位(左)和TDOA/FDOA联合定位(右)GDOP分布图

图3 T构型下TDOA定位(左)和TDOA/FDOA联合定位(右)GDOP分布图

图4 菱形构型下TDOA定位(左)和TDOA/FDOA联合定位(右)GDOP分布图

分析比较图2～4可以发现，在相同参数条件下，TDOA/FDOA联合定位的精度优于TDOA定位，且针对菱形构型，TDOA/FDOA定位精度的改善尤为明显，其GDOP以星下点为中心，均匀分布，而TDOA定位的GDOP则分布不均。

设绝对位置测量精度在0～300m连续取值，选取Y构型，其余参数不变，取星下点100km圆周上的一个点，分别仿真得到TDOA和TDOA/FDOA联合定位精度与绝对位置测量精度的关系曲线如图5和6所示。

比较图5和6可知，随绝对位置测量精度的提高，2种算法的定位精度都将随之提高。但是TDOA定位精度受绝对位置测量精度的影响很大，而TDOA/FDOA联合定位精度受绝对位置测量精度的影响非常小，相对于TDOA定位，该影响几乎可忽略不计。

图5 TDOA定位精度与绝对位置测量精度的关系曲线

图6 TDOA/FDOA联合定位精度与绝对位置测量精度的关系曲线

4 结束语

分析了四星TDOA定位算法和四星TDOA/FDOA联合定位算法的原理，分别推导了2种算法的GDOP表达式。通过仿真分析得出以下结论：

1) 在相同参数下，TDOA/FDOA联合定位算法比TDOA定位算法拥有更好的精度；

2) 在构型方面，特别针对于菱形，相较于TDOA定位算法而言，TDOA/FDOA联合定位算法不仅拥有更好的定位精度，且GDOP分布均匀情况也大为改善，解决了菱形构型分布不均的问题，增加了工程可实现性；

3) 相比于TDOA定位，TDOA/FDOA联合定位精度受卫星绝对位置测量精度的影响极小，减少了不可避免的绝对位置测量因素带来的定位误差。

[1] 单月晖, 孙仲康, 皇甫堪. 不断发展的无源定位技术[J]. 航天电子对抗, 2002，(1):36-42.

[2] 吴技. 国外航天侦察系统的现状与发展[J]. 电讯技术, 2009, 49(5):108-114.(WuJi.CurrentStatusandDevelopmentofForeignSpaceReconnaissanceSystems[J].TelecommunicationEngineering, 2009, 49(5):108-114.)

[3] 常新亚, 谢斌, 张晓敏,等. 双星TDOA/FDOA定位系统的目标定位精度分析[J]. 航天器工程, 2013, 22(4):35-42.(ChangXinya,XieBin,ZhangXiaomin,etal.TargetLocationAccuracyAnalysisofDual-satellitesLocationSystemUsingTDOAandFDOA[J].SpacecraftEngineering, 2013, 22(4):35-42.)

[4] 郭福成, 樊昀. 双星TDOA/FDOA无源定位方法分析[J]. 航天电子对抗, 2006, 22(6):20-23.(GuoFucheng,FanYun.AnalysisofDualSatellitesGeolocationMethodUsingTDOAandFDOA[J].AerospaceEletronicWarfare, 2006, 22(6):20-23.)

[5] 张勇, 盛卫东, 郭福成,等. 低轨双星无源定位算法及定位精度分析[J]. 中国惯性技术学报, 2007, 15(2):188-192.(ZhangYong,ShengWeidong,GuoFucheng,etal.LowOrbitDual-satellitesPassiveLocationAlgorithmandItsPrecisionAnalysis[J].JournalofChineseInertialTechnology, 2007, 15(2):188-192.)

[6] 刘丹军. 到达时间差与多普勒频率差联合定位方法研究[D]. 西安电子科技大学, 2010.(LiuDanjun.StudyofJointPassiveLocationUsingTimeDifferenceofArrivalandFrequencyDifferenceofArrivalMeasurements[D].XidianUniversity, 2012.)

[7] 郭文龙. 基于TDOA和FDOA多星联合定位技术研究[D]. 南京理工大学, 2009.

[8] 潘琴格, 严盟, 廖桂生. 多站时差和多普勒频差联合定位技术[J]. 雷达科学与技术, 2005, 3(6):332-335.(PanQinge,YanMeng,LiaoGuisheng.JointPassiveLocationUsingTDOAandFDOAinMulti-Stations[J].RadarScienceandTechnology, 2005, 3(6):332-335.)

[9] 尹锦荣, 程方铎, 李帅. 基于多站的时差和多普勒频差联合定位[J]. 现代雷达, 2008, 30(6):61-64.(YinJinrong,ChengFangduo,LiShuai.JointPassiveLocatingUsingTDOAandDopplerShiftBasedonMulti-Stations[J].ModernRadar, 2008, 30(6):61-64.)

Research on Precision Improvement of 4-Satellite Localization by Using TDOA/FDOA Algorithm

Zeng Botao1，Lu Haoran2, Guo Xiansheng1, Guo Yebo1, Liu Yang1

1.University of Electronic Science and Technology of China, Chengdu 611731, China 2.Beijing Institution of Astronautical Engineering, Beijing 100076, China

Inordertoimprovethelocationprecisionandprobabilityof4-Satellite-locationsysteminengineeringpractice,thefrequencydifferenceinformationbasedonthe4-SatelliteTDOA(TimeDifferenceofArrival)locationalgorithmisintroduced.TheTDOA/FDOA(FrequencyDifferenceofArrival)localizationalgorithmisusedtooptimizetheGDOPgeometricdilutionofprecision)of4-Satellitelocation.ThesimulationresultsshowthattheinfluenceofabsolutepositionmeasurementprecisiononthelocationprecisionofTDOA/FDOAisverysmallbycomparingwithTDOAlocation.Underthesameconditions,regardingthediamondconfiguration, TDOA/FDOAlocationhasbetterprecisionanditsGDOPhasmoreuniformdistribution.Thelocationprecisionof4-SatelliteTDOA/FDOAlocationisbetterthanthelocationprecisionof4-SatelliteTDOAlocation.

4-Satellitelocation;TDOA/FDOA;GDOP;Constellationconfiguration

2016-08-02

曾博韬(1993-)，男，四川金堂人，硕士研究生，主要研究方向为分布式定位；陆浩然(1982-)，男，合肥人，硕士研究生，副研究员，主要研究方向为飞行器总体；郭贤生(1979-)，男，安徽泗县人，博士，副教授，主要研究方向为无线定位、目标识别、机器学习及谱估计等；郭业波(1993-)，男，广西百色人，硕士研究生，主要研究方向为信息获取与探测技术；刘 洋(1990-)，男，安徽阜阳人，硕士研究生，主要研究方向为空间攻防。

P228.1

J

1006-3242(2017)02-0031-06