基于2D/3D多特征融合的近距离空间非合作目标相对测量方法*

易 兵 敬忠良 潘 汉

上海交通大学航空航天学院，上海 200240



基于2D/3D多特征融合的近距离空间非合作目标相对测量方法*

易 兵 敬忠良 潘 汉

上海交通大学航空航天学院，上海 200240

面向空间在轨服务重大应用需求，以提高系统自主性和空间环境适应性为目标，发展了一种空间非合作目标三维重建、目标识别和位姿估计一体化的近距离相对测量方法。该方法基于二维图像信息和深度数据，通过数据融合并重建出非合作目标的稠密三维模型，接着基于快速迭代最近点配准算法，提出基于SIFT和SHOT特征融合的三维识别方法，为系统的相对位姿估计提供有效的参数初始化。本文方法可进一步减少地面的干预，增强在轨服务系统的自主性，扩展系统的工作范围。地面仿真实验验证了该方法的可行性和有效性。 关键词 非合作目标；相对位姿测量；三维重建；三维目标识别

空间非合作目标近距离相对测量是卫星在轨服务中的关键技术之一[1]。它为服务卫星接近、捕获空间非合作目标，开展修理维护等空间任务提供关键导航支持。

空间非合作目标相对测量受到各国科研人员的关注。美国FREND项目[2]、欧空局TECSAS/DEOS项目[3]和欧洲多国合作的PRISMA项目[4]都使用了视觉测量载荷确定非合作目标的相对位置和姿态。加拿大Neptec公司开发了基于激光雷达的视觉系统TriDAR，并通过三维点云配准的方式来测量非合作目标[5]。我国在这个领域的研究亦活跃而有成果。郝刚涛[6]和张劲锋[7]等分别提出了基于单目相机的航天器相对位姿测量方法。徐文福等基于图像形态学特征，提出了相对测量的双目视觉系统[8]。刘涛等从相对距离、姿态确定，以及滤波器设计的角度研究了非合作目标相对导航方法[9]。王晓亮等研究了噪声不确定情况下的非合作目标对接滤波器算法[10]。徐培智提出了结合双目相机和激光扫描仪的非合作目标相对测量方案。其中，激光扫描仪用于确定相对距离信息[11]。最近，梁斌等分析了ToF相机应用在空间非合作目标近距离相对测量的可行性，梳理了其中的关键技术，并对发展趋势进行展望[12]。

空间非结构化环境下的特征检测与跟踪、帧与帧配准带来的误差累积问题给基于可见光图像的测量方法带来了极大挑战。目前，基于三维模型配准的测量方法依赖于目标几何模型的建立。本文使用深度传感器和可见光相机，结合三维重建和三维目标识别技术，提出一种融合2D彩色信息和3D几何信息特征的近距离空间非合作目标相对测量方法。该方法通过在线重建，并获取非合作目标三维模型，减小对先验信息的依赖；然后，通过帧与重建模型配准的方式，减小测量误差累积；最后，基于三维目标识别方法，解决位姿参数初始化和测量失败下的重新定位问题，增强了系统自主性与环境适应性。

首先从总体上介绍了本文方法的3个运行阶段和对应的飞行状态，随后具体讲述方法的各个环节，给出了算法地面仿真实验与分析结果，最后总结并指出可能改进的方向。

1 非合作目标相对测量过程概述

本文结合三维重建技术和三维目标识别技术增强系统自主性的目的，提出一种非合作目标近距离相对测量的方法。即服务卫星抵近目标卫星，以及相对测量的相对飞行轨迹，如图1所示。在发现并靠近目标达到一定距离之后，服务卫星开始对目标卫星进行相对测量。这个过程中有2种飞行状态：

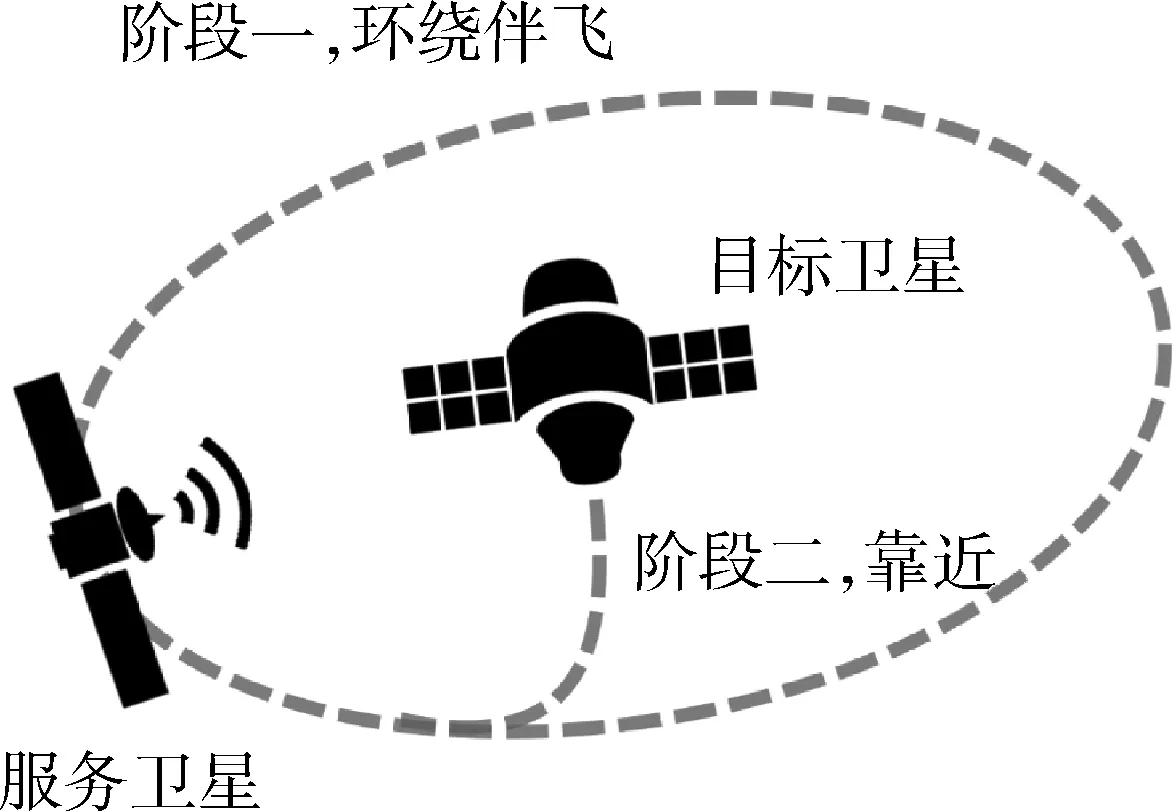
图1 相对测量理想相对飞行轨迹

1)服务卫星环绕目标卫星伴飞。其中，服务卫星对目标卫星展开连续观测，对非合作目标进行三维重建，接着进行三维目标识别，识别目标形态以给出相对测量初始参数；

2)服务卫星停止环绕伴飞，以合理路线靠近非合作目标以进行对接。其中，服务卫星借助绕飞阶段重建的目标模型对非合作目标进行准确的相对测量，为对接捕获做准备。

与两卫星2种飞行状态相联系的是服务飞行相对测量系统的3种工作阶段：三维重建阶段、三维目标识别阶段和相对测量阶段。整个工作流程如图2所示(图中目标运动状态分析阶段是利用相对测量采集的数据分析目标的运动参数，此阶段不在本文关注范围内)。

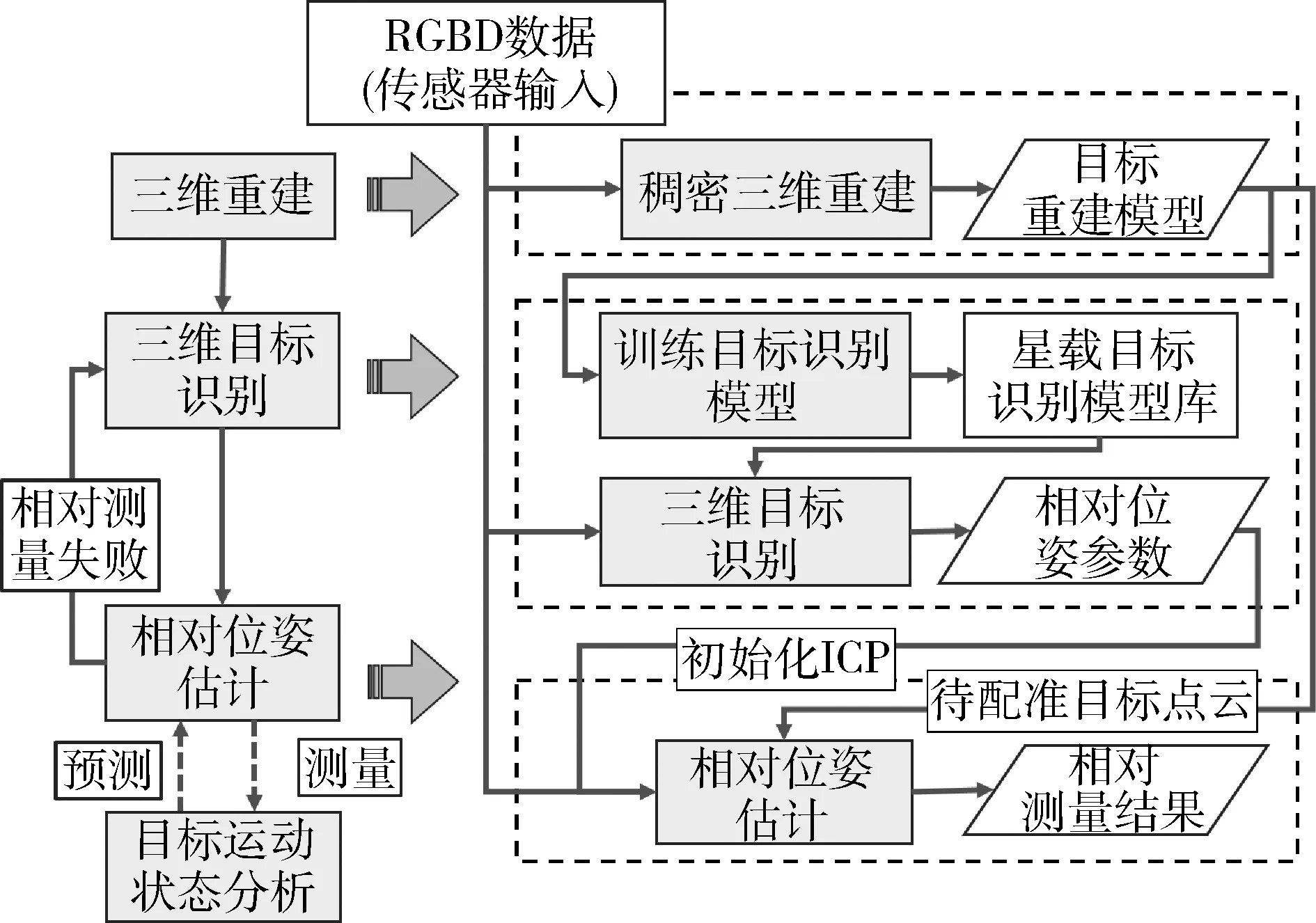
图2 非合作目标相对测量系统流程图

1)三维目标重建阶段。系统采集可见光传感器和激光成像传感器的测量数据，通过相对运动位姿估计将连续观测的目标数据融合，通过稠密三维重建算法获取非合作目标的曲面模型；

2)三维目标识别阶段。使用三维目标识别有2个目的：①为相对测量提供初始化相对位姿参数；②在相对测量失效需要重置的情况下，找回当前相对位姿。三维目标识别首先以重建模型为输入训练目标识别模型，然后再对传感器输入进行三维目标识别，给出相对测量的初始位姿参数；

3)在相对测量阶段，使用迭代最近点算法将传感器采集数据与非合作目标模型数据进行配准，计算出当前时刻目标相对位置和姿态参数。

本文提出的非合作目标相对测量系统方案在不同阶段下分别完成建模、识别、相对测量等工作，减少系统对非合作目标先验信息的需求，为服务卫星提供准确的相对测量数据。以下详细介绍本文方法内容。

2 非合作目标相对测量方法

2.1 相对位姿估计

相对位姿估计是相对测量系统的核心。本文使用迭代最近点(Iterative Closest Point，ICP)算法[13]进行相对位姿计算。

Newcombe等人通过实验验证了使用帧-模型的ICP配准计算的时间漂移小于使用帧-帧ICP配准的时间漂移[14]。因此，本文使用输入帧数据与重建模型数据ICP配准策略。ICP算法普遍采用的步骤，如图3所示。该算法将输入点云与目标点云进行配准计算。在一次迭代计算过程中，ICP算法首先搜索输入点云与目标点云之间的匹配点，再经过匹配点对筛选之后进行旋转矩阵和位移向量的最小二乘估计，得到相对变换的增量变换。在此基础上，应用增量变换更新输入点云，并且更新误差函数，然后进入下一次迭代。

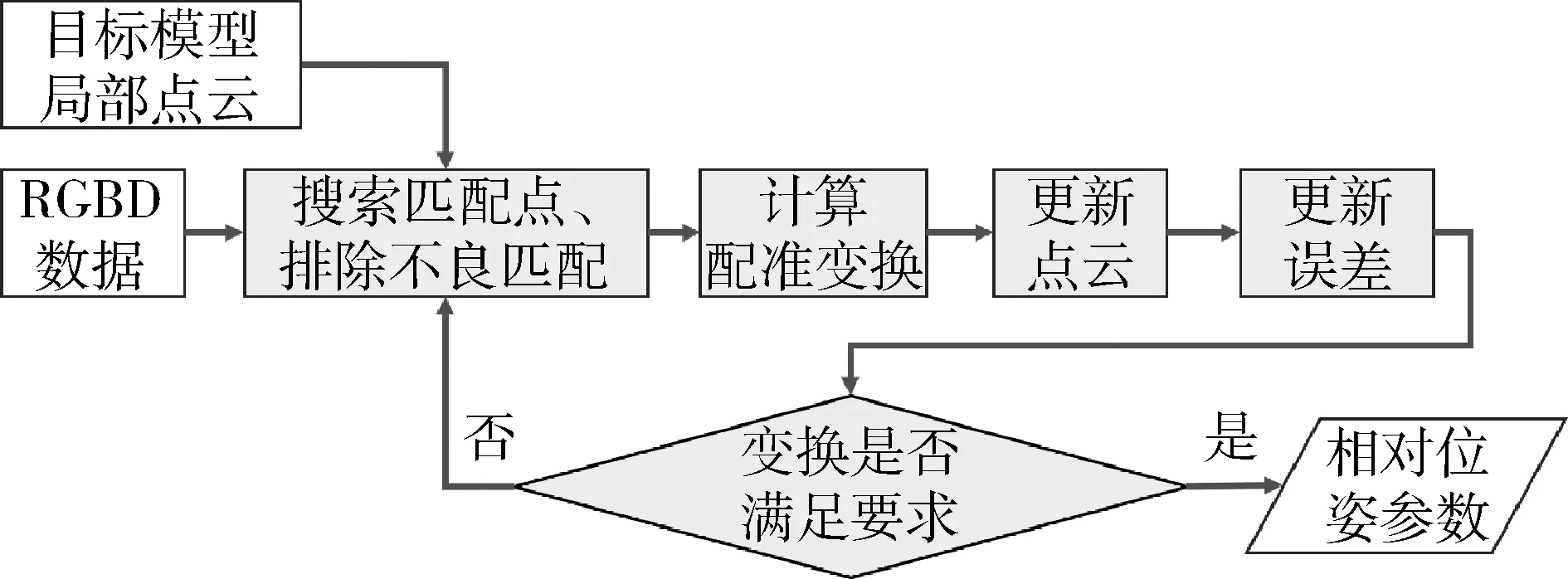
图3 ICP算法流程

2.1.1 ICP输入点云计算

首先利用输入的深度图像计算输入点云对应的三维坐标。然后采用均匀采样方法采集ICP配准控制点，降低计算量。已知深度传感器的内参数，从深度图像生成点云的计算过程如下。

在简化的针孔相机投影模型下，相机的投影矩阵为：

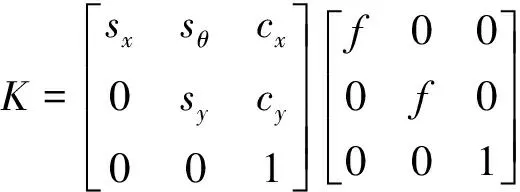
(1)

式中，sx，sy和sθ是相机的像素缩放因子，f是相机焦距，cx和cy是图像中心位置对应像素坐标。在齐次坐标表示下，相机的投影模型为：

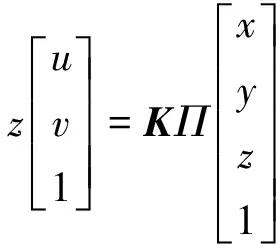
(2)

其中，Π是标准投影矩阵：

对于深度图像，D(u,v)=z/sz，sz是Z轴缩放因子，对于常见的Kinect传感器其值为1000mm。于是对应图像坐标点(u,v)的三维空间点p(u,v)的坐标是：

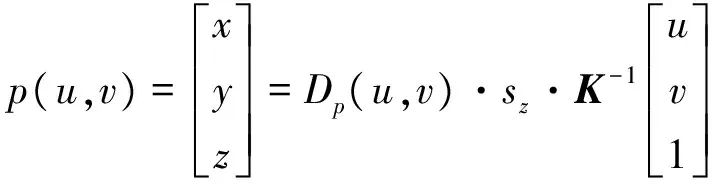
(3)

2.1.2 匹配点搜索与筛选

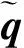
(4)

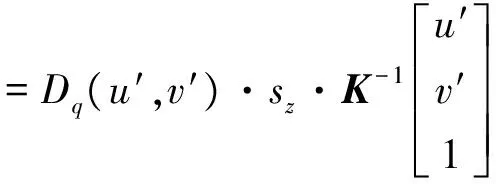
(5)

2.1.3 误差函数与最优化求解

本文使用点到平面的距离的平方之和[14]作为误差函数。在第k次ICP迭代中，误差函数定义为：

(6)

(7)

ΔT属于特殊欧拉群SE(3)，隐含着复杂的约束条件，使得此最优化问题难以直接求解。考虑到卫星间相对运动速度缓慢，输入点云与待配准的目标点云之间相对运动量小，可以假设ΔT很小：

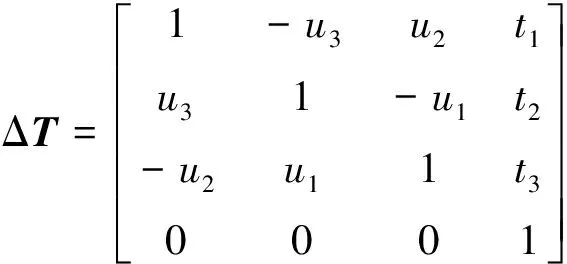
于是ek(ΔT)可以改写成x的函数：

(8)

式(9)中映射A:3|→4×6为：

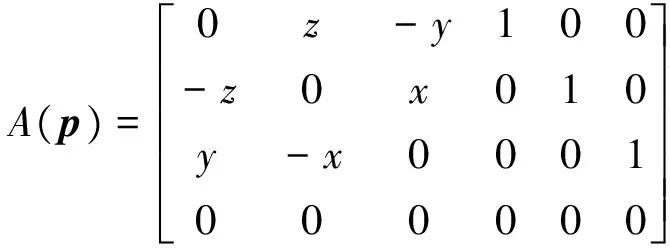
x=[u1,u2,u3,t1,t2,t3]T

相应的问题式(7)变为：

(9)

使用非线性优化算法或者简单最小二乘方法可方便求解出x*以及对应的增量变换ΔT*。

2.2 非合作目标稠密三维重建

对非合作目标表面进行深度测量得到的是不连续且含有噪声的数据。高效率地从这些数据中重建目标模型是比较困难的。采用传统的顶点——网格——曲面的三维重建计算量太大，不能达到实时要求。KinectFusion[14]算法提出了高效的解决方法。该方法以立方体体素表达模型空间，通过融合TSDF(TruncatedSignedDistanceFunction)有向距离函数完成对目标场景快速、准确重建。本文提出的稠密三维重建流程如图4所示。读取传感器数据后按照深度图像计算点云及法向量，使用2.1节的快速ICP算法计算输入数据到重建模型的相对位姿变换。然后进行TSDF点云融合更新重建模型。最后使用虚拟相机采集重建模型的局部视图。本节讲述后2个步骤。

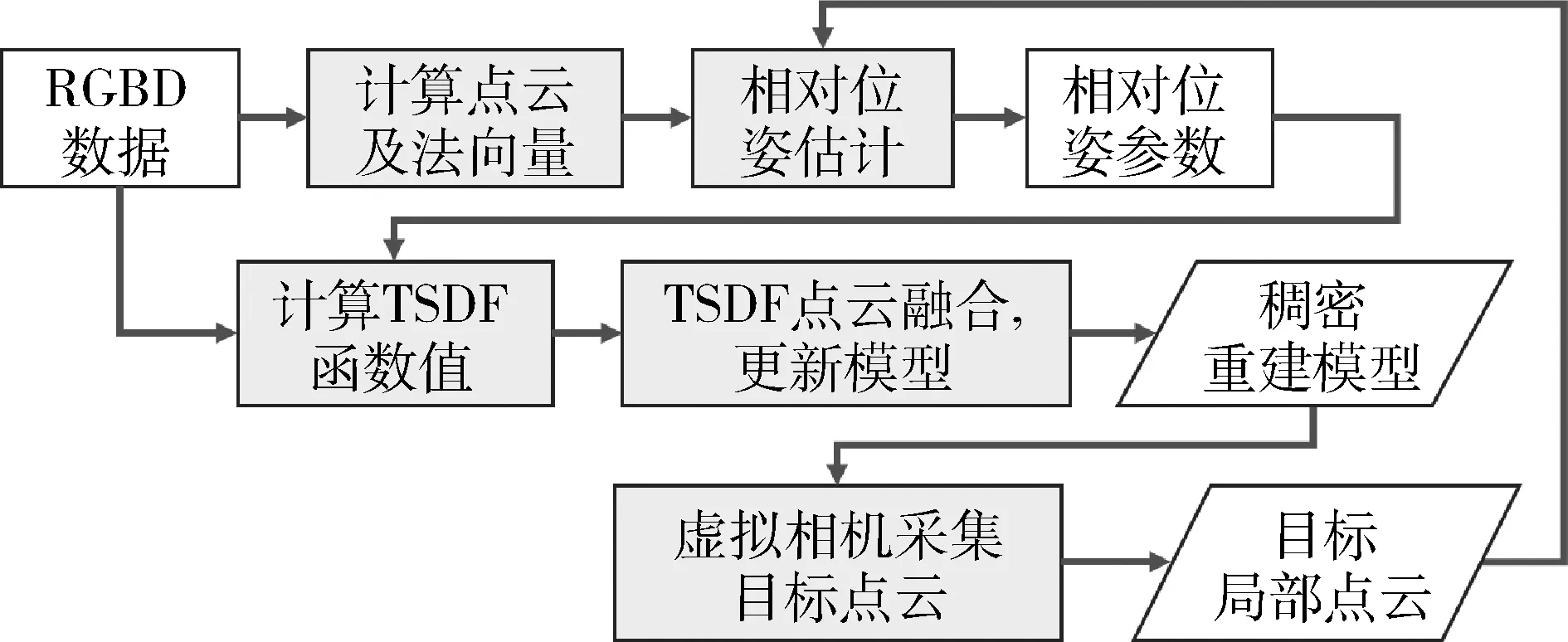
图4 稠密三维重建流程图

2.2.1 稠密三维重建

首先在全局坐标系下将测量空间划分为N×N×N个立方体体素(Voxel)。然后给每一个体素赋予一个有向距离值Fk(p)和一个融合权值Wk(p)(p表示体素中心的三维坐标)。Fk(p)表示该体素距测量到的非合作目标表面的有向距离：Fk(p)=0表示目标表面正好穿过此体素；Fk(p)>0表示体素位于非合作目标表面上的空白空间；Fk(p)<0则表示体素处于非合作目标表面之下的空间，实际上是传感器无法测量到的。

TSDF点云融合方法具有最小二乘优化性质，对传感器噪声具有一定的滤波作用。在相对测量模块求解出当前深度图像Dk的配准变换Tg,k之后，其在全局坐标系下的TSDF函数表示[FDk,WDk]的计算为：

(10)

其中：

在建模精度损失不大的情况下，可设定Wdk(p)=1。当前深度测量与全局重建模型的融合公式为(Fk(p)≠null)：

(11)

Wk(p)=min(Wk-1(p)+WDk(p),Wthres)

(12)

2.2.2 相对位姿估计模块目标点云数据获取

将一虚拟深度相机以与卫星下一时刻预测的位置和朝向对非合作目标的重建模型进采样。假设光线从虚拟相机中心朝每一个像素点方向射出，如果遇到体素的有向距离Fk(p)从正到负变化，就以此光心到零跨越处的深度作为图像采样值。具体过程参考文献[14]。通过这个步骤，可以获得相对位姿估计系统所需要的目标模型深度图像、目标模型点云和对应的法向量。

2.3 三维目标识别

本文提出基于多特征融合的非合作目标三维识别方法。首先训练非合作目标模型，然后对传感器输入进行三维目标识别，给出相对测量的初始位姿参数，具体算法流程如图5所示。

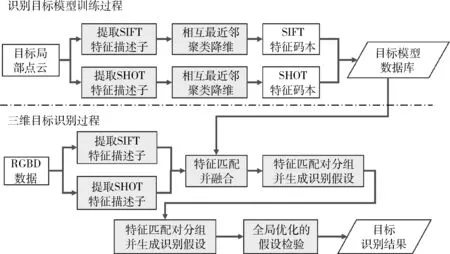
图5 三维识别流程图

2.3.1 训练三维目标识别模型

训练三维目标识别模型以待识别目标三维模型，且包含彩色信息的局部点云作为输入。在提取RGB-D数据的二维SIFT特征和三维SHOT特征后，分别使用相互最近邻算法(ReciprocalNearestNeighborClustering)[17]对两类特征描述子码本进行降维处理，得到方便高效搜索的特征描述子码本。最后将码本存储以完成非合作目标三维识别模型的训练。

2.3.2 三维目标识别

基于多特征融合的非合作目标三维识别方法融合二维图像SIFT(ScaleInvariantFeatureTransform)特征[18]和三维SHOT(SignatureofHistogramsofOrientations)特征[19]的描述能力，通过匹配对分组聚集符合几何约束的特征匹配对，并使用全局优化的假设检验方法筛选最佳相对测量结果。如图5所示，三维目标识别按照步骤进行，详细描述可参考文献[20]：

1) 读取传感器输入数据；

2) 分别提取二维SIFT特征和SHOT特征；

3) 将以上特征与训练数据特征进行匹配，并将二维SIFT特征匹配对映射到三维空间；

4) 根据几何一致性约束将特征匹配对分组，并在每组中估计一个识别假设hi={Mi,Ti}(Mi是识别标签，Ti是配准变换)；

5) 以X=[x1,x2,…,xn]T,xi∈B={0,1}表示所有识别假设hi被接受或拒绝的状态，计算全局目标函数F(X)，并使用模拟退火算法搜索最优解。

该算法具备同时识别多个模型的能力，当模型数量只有一个时，算法退化成对所有模型假设进行逐一检验的方法。

3 地面仿真实验

为评估算法的可行性和有效性，本文基于华硕XtionProLiveRGB-D传感器(模拟空间可见光相机与无扫描激光雷达)，开展相对测量地面仿真实验。该传感器在2m处的深度测量精度约2mm[21]。以下实验中均保持传感器和待测量卫星模型之间的距离在2m内。

1)相对位置测量实验

相对距离测量实验中卫星模型固定，传感器沿某个方向等间距平移，将相邻2次测量结果ti+1和ti之间的差值与真值进行对比来确定该方法在相对距离测量上的精度：

Δt=ti+1-ti

设置不同平移值，展开了2次实验： Δt1=[0,0,0.05m]T，Δt2=[0.05m,0,0.05m]T。2次测量结果的误差参见表1。结果显示相对位置测量精度与传感器测量精度相当，而且在传感器特性影响下纵向测量精度明显高于横向测量精度。

2)相对姿态角测量实验

相对姿态角测量实验为固定传感器位置和姿态，固定卫星模型位置，沿空间某个固定轴u旋转指定角度θ。比较前后相对姿态测量的姿态矩阵Ri和Ri+1，然后通过旋转矩阵的欧拉角分解得到旋转轴u和旋转角θ：

本文进行了2次实验，实验中卫星模型分别围绕未知的轴旋转2次，每次旋转20°。相对姿态角测量结果如图6所示。本文算法相对姿态角测量的绝对误差和标准差分别是：

第1组实验：E1=0.6297°,σ1=1.5120°,

第2组实验：E2=0.2627°，σ2=1.1479°

表1 相对位置测量绝对误差和标准差

图6 相对姿态角测量实验旋转角θ结果

4 结论

以增强非合作目标近距离相对位姿测量系统自主性为目标，提出了综合三维重建、目标识别和位姿估计3个部分的非合作目标相对位姿测量方法。该方法以快速ICP算法、TSDF点云融合算法和基于多特征融合的三维目标识别算法为核心，进一步降低了系统对非合作目标先验信息的依赖，提高了系统自主性，增强了相对位姿测量精度和空间环境适应性。综合多源信息的处理过程在一定程度上以系统复杂度增加为代价，后续研究将以本文方法为基础，进一步深入研究重建、识别和位姿估计一体化系统，降低算法的时空复杂度，提高系统实时性，扩展系统的空间环境应用范围。

[1] 梁斌, 杜晓东, 李成,等. 空间机器人非合作航天器在轨服务研究进展[J]. 机器人, 2012, 34(2):242-256. (Liang Bin, Du Xiaodong, Li Cheng, et al. Advances in Space Robot On-orbit Servicing for Non-cooperative Spacecraft[J]. Robot, 2012, 34(2):242-256.)

[2] Debus T, Dougherty S. Overview and Performance of the Front-End Robotics Enabling Near-Term Demonstration (FREND) Robotic Arm[C]. AIAA Infotech, Aerospace Conference, 2009.

[3] Martin E, Dupuis E, Piedboeuf J C, et al. The TECSAS Mission from a Canadian Perspective[C]. Proc. 8th International Symposium on Artificial Intelligence and Robotics and Automation in Space, Munich, Germany, 2005.

[4] Persson S, Bodin P, Gill E, et al. PRISMA - An Autonomous Formation Flying Mission[C]. Small Satellite Systems and Services - The 4S Symposium. DLR, 2006.

[5] Ruel S, English C, Anctil M, el al. 3DLASSO: Real-time Pose Estimation from 3D Data for Autonomous Satellite Servicing[C]. Proc. of The 8th International Symposium on Artifical Intelligence, Robotics and Automation in Space, Germany, 2005.

[6] 郝刚涛, 杜小平. 基于单目视觉图像序列的空间非合作目标相对姿态估计[J]. 航天控制, 2014, 32(2):60-67. (Hao Gangtao, Du Xiaoping. Relative Attitude Estimation for Space Non-cooperative Targets Based on Sequence of Monocular Images[J]. Aerospace Control, 2014, 23(2):60-67.)[7] 张劲锋, 蔡伟, 孙承启. 基于单目视觉的空间非合作目标相对运动参数估计[J]. 空间控制技术与应用, 2010, 36(2):31-35. (Zhang Jingfeng, Cai Wei, Sun Chengqi. Monocular Vision-Based Relative Motion Parameter Estimation for Non-Cooperative Objects in Space[J]. Aerospace Control And Application, 2010, 36(2):31-35.)

[8] 徐文福, 梁斌, 李成,等. 基于立体视觉的航天器相对位姿测量方法与仿真研究[J]. 宇航学报, 2009, 30(4):1421-1428. (Xu Wenfu, Liang Bin, Li Cheng, et al. The Approach and Simulation Study of the Relative Pose Measurement Between Space-crafts Based on Stereo Vision[J]. Journal of Astronautics, 2009, 30(4): 1421-1428.)

[9] 刘涛, 解永春. 非合作目标交会相对导航方法研究[J]. 航天控制, 2006, 24(2):48-53. (Liu Tao, Xie Yongchun. A Study on Relative Navigation for Spacecraft Rendezvous with a Noncooperative Target[J]. Aerospace Control, 2006, 24(2):48-53.)

[10] 王晓亮, 邵晓巍, 龚德仁,等. 改进的量测噪声自适应滤波在空间非合作目标视觉导航中的应用[J]. 航天控制, 2011, 29(2):37-41. (Wang Xiaoliang, Shao Xiaowei, Gong Deren, et al. Application of an Improved Measurement Noise Adaptive Filter in Vision Navigation for Non-Cooperative Target in Space[J]. Aerospace Control, 2011, 29(2):37-41.)

[11] 徐培智. 基于视觉和激光的空间非合作目标相对位姿测量技术研究[D]. 南京航空航天大学, 2014. (Xu Peizhi. Research on Measurement of Relative Pose Between Space Non-cooperative Targets Based on Vision and Laser[D]. Nanjing University of Aeronautics and Astronautics, 2014.)

[12] 梁斌, 何英, 邹瑜,等. ToF相机在空间非合作目标近距离测量中的应用[J]. 宇航学报, 2016, 37(9):1080-1088. (Liang Bin, He Ying, Zou Yu, et al. Application of Time of Flight Camera for Relative Measurement of Non-Cooperative Target in Close Range[J]. Journal of Astronautics, 2016, 37(9) :1080-1088. )

[13] Rusinkiewicz S, Levoy M. Efficient Variants of The ICP Algorithm[C]. 3-D Digital Imaging and Modeling, 2001. Proceedings. Third International Conference on. IEEE, 2001.

[14] Newcombe R A, Izadi S, Hilliges O, et al. Kinect Fusion: Real-time Dense Surface Mapping and Tracking[C]. IEEE International Symposium on Mixed and Augmented Reality. IEEE, 2011:127-136.

[15] Blais G, Levine M D. Registering Multiview Range Data to Create 3D Computer Objects[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1995, 17(8):820-824.

[16] Rusinkiewicz S, Hall-Holt O, Levoy M. Real-time 3D Model Acquisition[J]. Acm Transactions on Graphics, 2010, 21(3):438-446.

[17] Leibe B, Leonardis, Ales, Schiele B. Robust Object Detection with Interleaved Categorization and Segmentation[J]. International Journal of Computer Vision, 2008, 77(1-3):259-289.

[18] Lowe, D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision,2004,60(2): 91-110.

[19] Tombari F, Salti S, Stefano L D. Unique Signatures of Histograms for Local Surface Description[C]. ECCV 2012. Springer Berlin Heidelberg, 2010.

[20] Aldoma A. A Global Hypotheses Verification Method for 3D Object Recognition[C]. ECCV 2012. Springer Berlin Heidelberg, 2012:511-524.

[21] Rauscher G, Dube D, Zell A. A Comparison of 3D Sensors for Wheeled Mobile Robots[M]. Intelligent Autonomous Systems 13. Springer International Publishing, 2016:29-41.

2D/3D Feature Fusion Based on Space Non-Cooperative Target Close-Range Relative Measurement

Yi Bing， Jing Zhongliang，Pan Han

Shanghai Jiao Tong University, Shanghai 200240, China

Aclose-rangerelativemeasurementmethodfor3Dreconstruction,objectrecognitionandrelativeposeestimationofspacenon-cooperativetargetintegrationisdevelopedtofulfillthegoalofimprovedsystemautonomyinthescenarioofon-orbitsatelliteservicing.Thetwo-dimensionalRGBdataanddepthdataarefusedtoapplyintheproposedmethod,andadense3Dmodelisestablishedbytruncatedsigneddistancefunction,thena3DobjectrecognitionpipelinebasedonintegrationionofSIFTdescriptorandSHOTdescriptorisproposedtoapplytothereconstructedmodelforinitializingeafastversionofiterativeclosestpointregistrationcycle.Therefore,thevalidparametersofrelativeposeestimationcanbecalculated.Theautonomyofthesystemcanbeenhancedandtheadaptabilityofrelativeposemeasurementpipelinecanbeimprovedbyusingthismethod.Groundsimulationdemonstratesthefeasibilityofthismethod.

Non-cooperativetarget;Relativeposemeasurement; 3Dreconstruction; 3Dobjectrecognition

* 国家自然科学基金资助项目(61673262，61603249)；上海市科学技术委员会重点资助项目(16JC1401100)

2016-10-25

易 兵 (1991-)，男，湖南人，硕士研究生，主要研究方向为航空宇航信息与控制；敬忠良 (1960-)，男，四川人，教授、博士生导师，主要研究方向为航空航天信息处理与控制，信息融合；潘 汉 (1983-)，男，广西人，博士，助理研究员，主要研究方向为黎曼流形优化与信息融合。

TP242

A

1006-3242(2017)02-0060-06