采用混合推进下的库仑卫星编队重构控制研究

王 婷

南京工业大学电气工程与控制科学学院，南京211816



采用混合推进下的库仑卫星编队重构控制研究

王 婷

南京工业大学电气工程与控制科学学院，南京211816

提出以库仑力为主、电推进为辅助的混合推进，用以解决库仑卫星编队在碰撞规避过程中的重构控制问题，重构控制采用模糊最优二次型控制，最后通过仿真进行了验证。 关键词 混合推进；库仑卫星编队；碰撞规避；重构控制

近年来，极近距离库仑卫星编队(10～100m)倍受关注。由于地球同步轨道(GEO)存在天然的电磁场，King和 Schaub[1-3]等人提出了一种利用卫星间的静电力实现卫星编队飞行的新概念。通过释放带正电荷或带负电荷的粒子，使卫星编队受到库仑静电力的控制。通过对极近距离编队卫星表面产生不同的电荷，每个卫星对所有其他卫星都产生引力或斥力，这种作用力可以使具有库仑静电力的库仑卫星编队形成并维持十米量级的队形[4-7]。库仑静电力利用可再生的电能源，在控制卫星的相对运动过程中不会产生污染[8]，且可应用于未来的极近距离编队飞行任务中。

大多数的商业卫星和通讯卫星发射在GEO轨道附近。许多已废弃的卫星并未达到最终寿命，仍然占据在地球静止轨道中，这势必影响新卫星的发射。废弃的卫星群由于没有精确的轨道控制而发生漂移，在月球和太阳辐射干扰影响下，这些废弃卫星群会徜徉在地球静止轨道附近，对GEO上的在役卫星造成极大的碰撞威胁。截至目前为止，有超过1100颗位于地球静止轨道的物体被跟踪到，只有不到400颗的卫星可以进行位置姿态保持控制[9]。因此，研究库仑卫星编队的碰撞规避十分重要。

在实际卫星编队的碰撞规避过程中，很多机动需要大幅度转向，但所有静电库仑作用力都是内部力，并不能改变卫星惯性轴的角动量。而且库仑编队的动力学模型是具有高度耦合的非线性模型，使得单纯依靠静电库仑力无法满足碰撞规避过程中的推进需求。电推进由于比冲高、精度高等特性，非常适合作为小卫星的轨道机动推进系统。但单纯的电推进器喷射出的粒子会对近距离编队的邻近卫星造成羽流污染，必须加以避免。因此，考虑库仑力与电推进器共同作用的混合推进方式，通过以库仑推进为主，电推进为补充的混合推进，既能避免单纯库仑推进无法转向的弊端，又可以极大降低电推进器功率，从而避免羽流污染，实现极近距离带电卫星编队的碰撞规避过程。

目前已有的关于库仑编队重构控制方面的研究论文很多都仅依靠库仑静电力作为推进动力，如文献[10]最早开展了三星库仑卫星编队一维队形保持控制和重构的研究，通过设计具有李亚普诺夫函数的反馈控制实现编队的保持和重构。文献[11]在文献[12]之后继续了三星库仑卫星编队平面三角队形下的队形保持控制和重构。文献[13]是最早考虑万有引力作用的单纯库仑静电力编队控制的文章，提到了卫星空间位置与速度对队形控制的影响，控制方法为最简单的反馈控制。然而这些早期研究较多关注静态下库仑卫星的重构过程以及重构控制问题，因此只适用于编队内部结构的微小变化而不适合进行瞬时大幅转向的碰撞规避过程。文献[14]首次提出了混合推进概念，即以库仑静电力推进为主、电推进为辅的混合推进，并采用滑模控制方法进行了仿真验证。但其不足之处在于滑模控制本身不可避免的在过程中发生抖颤现象，从而影响整个重构过程的稳定性以及忽略羽流对具有极近距离编队的库仑卫星编队的污染。

脉冲等离子体推进器(Pulsed Plasma Thruster，简称PPT)是电推进的一种，它具有比冲高、推重比小、体积小、质量轻、寿命长和结构简单的特点，是微小卫星很理想的动力装置。在空间执行任务时，在任务相同的条件，PPT和其它电推进系统相比在系统质量和成本、性能等方面具有非常大的优势，且非常适合微小卫星的推进。然而对于极近距离的带电库仑卫星编队，必须对PPT的放电电压和放电电流进行控制，从而使羽流对邻近卫星的损害可以忽略[15-18]。

鉴于前期关于库仑卫星编队的构型研究和静态重构过程的研究[19-22]，本文继续研究混合推进下库仑卫星编队的碰撞规避过程，并着重研究碰撞规避过程中的重构控制方法。鉴于已有混合推进研究中重构控制方法的弊端，本文采用模糊最优二次型控制方法，通过对重构控制引入模糊优化，可以使电推进器的推力随着卫星间距的变化而相应增减，且有效避免了电推进对邻近卫星的羽流影响。

1 库仑编队的动力学方程

假设编队卫星重构前后的队形均为等边三角形，分别为图1中虚线(重构前队形，卫星1,2,3)和实线(重构后队形，卫星1′,2′,3′)所示，虚线弧段分别为各星重构路径。假设质心(Center of Mass, CM)绕地沿如图1所示轨道做运动，编队的质心位于希尔坐标系的原点，而为了维持编队稳定的静态构型，不使编队绕着任一惯性主轴旋转，编队具有对称结构，即惯性轴转动惯量的交叉项为0。质心和卫星i-th相对于地球的距离分别为ρcm和ρf，二者之间的相对距离为ρ。卫星i-th和卫星j-th之间的距离为Lij，在万有引力和静电力作用下的卫星编队的动力学方程为[22]：

图1 库仑卫星编队重构前后的编队队形

(1)

假设重构过程之中卫星间距均相等，则简化后的线性定常控制模型为：

(2)

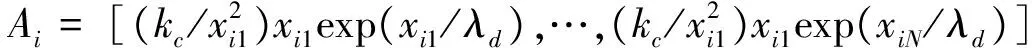
式(2)中,L2=(xi-xj)2+(yi-yj)2+(zi-zj)2，也即等式右边第2部分的分子含有状态变量x,y,z，而分母为状态变量的函数，此时为线性时变系统，为了方便仿真计算，此处将L取为重构前后队形间距的平均值。

(3)

状态反馈K=R-1BTP，其中P是Riccati代数方程ATP+PA-PBR-1BTP+Q=0的唯一正定对称解。

2 对LQR重构和电推进器的控制改进

基于LQR理论设计的最优控制器可以实现卫星编队的构型重构控制，但是由于控制律完全由系统状态方程决定，构形重构时间与电推进随Q和R的选择而完全确定，若能考虑编队运行时的信息灵活设计控制器，将更好地满足编队自主运行的要求，为此设计一个如图2所示的模糊逻辑控制器来改变和调节控制器的性能。模糊逻辑控制器以位置跟踪误差和电推进输入作为系统输入，其模糊集合的隶属度函数分别如图3(a)和(b)所示，选取4组Q和R， 将4种情况下的控制增益K按照推力极小(B)，较小(W)，适中(Z)和稍大(D)的顺序，采用的模糊推理规则如表1所示。

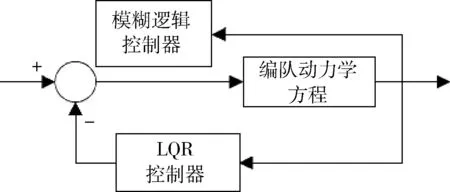
图2 加入模糊逻辑控制器的原理图

图3 隶属度函数和电推进推力以及星间距的关系图

表1 模糊规则推理表

M/K/EVeryCloseCloseMidrangeFarNotCritialBBWZNormalBWZDCritialWZDD

3 仿真以及实验

如图1所示，为了简便，重构前后的队形均为等边三角形，间距分别为50m和20m，此处也可以换为多星其它静态平衡构型。等离子体推进器的参数如下：功率为1500w,峰值推力为80mN,脉冲为1600s,放电电压为300V, 效率为55%。卫星1,2,3的质量分别为50kg, 150kg, 100kg, 德拜长度取180m。

仿真结果如图4所示，图4(a),(b),(c)分别为卫星1,2,3的位置和速度变化图，图4(d)和(e)分别为静电力推进和等离子体推进的输入电容量和推力。通过加入模糊优化，推进器输出的推力随卫星间距的减小而减小，当卫星间距较大时，电推进推力输入较大，而当卫星之间间距逐渐减小到期望的紧凑队形后，电推进器最终维持在较低的输入推力，实现了作为静电力推进补偿的推进力。由于等离子体在较低的放电电压下工作，并且保持较低的工作效率，电推进器对邻近卫星的羽流影响可以忽略不计。通过仿真可以得出，在以静电力推进为主，电推进为补充的混合推进下，极近距离的库仑卫星编队实现了队形重构。

图4 仿真结果

4 结论

研究了在混合推进器作用下，库仑卫星编队的碰撞规避重构过程。由于库仑力属于内部力，无法实现卫星编队的转向，而单纯依靠电推进会对具有极近距离的库仑卫星编队造成羽流污染。在碰撞规避的重构过程中，库仑卫星编队往往需要大幅瞬时转向，因此设计以静电推进力为主，以电推进为补充的混合推进既能弥补静电力推进的不足又可以有效避免羽流。重构控制采用加入模糊推力环节的LQR最优控制方法，并通过仿真加以验证。从仿真结果看出，本文设计的重构控制方法实现了库仑卫星编队的队形重构过程。今后的工作将会继续围绕混合推进在库仑卫星编队中的应用，包括碰撞规避过程中的路径规划、队形保持控制，编队的自重组和自修复等内容。

[1] King L, Parker G, Deshmukh S， et al. Propellantless Control of Spacecraft Swarms Using Coulomb Forces [J]. NIAC Final Report, 2002.

[2] King L, Parker G, Deshmukh S, et al. Spacecraft Formation-Flying Using Inter-Vehicle Coulomb Forces[J]. Tech. Report, NASA/NIAC, http://www.niac.usra.edu/, 2002.

[3] King L, Parker G, Deshmukh S, et al. Study of Inter-spacecraft Coulomb Forces and Implications for Formation Flying [J]. AIAA Journal of Propulsion and Power, 2003, 19(3): 497-505.

[4] Schaub H, Parker G, King L. Challenges and Prospects of Coulomb Spacecraft Formations[C]. AAS John L. Junkins Astrodynamics Symposium, College Station, TX, 2003, Paper No. AAS-03-278.

[5] Schaub H. Stabilization of Satellite Motion Relative to a Coulomb Spacecraft Formation[C]. AAS Spaceflight Mechanics Meeting, Maui, Hawaii, 2004, Paper No. AAS 04-259.

[6] Joe H, Schaub H, Parker G. Formation Dynamics of Coulomb Satellites[C]. 6thInt. Conf. on Dynamics and Control of Systems and Structures in Space, Cinque Terre, Liguria, Italy, 2004.

[7] Schaub H. Kim M. Orbit Element Difference Constraints for Coulomb Satellite Formation[C]. AAS Astrodynamics Specialist Conference, Providence, Rhode Island, 2004, Paper No. 04-5213.

[8] Berryman J. Schaub H. Static Equilibrium Configurations in GEO Coulomb Spacecraft Formations[C]. AAS Spaceflight Mechanics Meeting, Copper Mountain, CO, 2005, Paper No. 05-104.

[9] Natarajan A, Schaub H. Linear Dynamics and Stability Analysis of a Coulomb Tether Formation[C]. AAS Spaceflight Mechanics Meeting, Copper Mountain, CO, 2005, Paper No. 05-204.

[10] Hanspeter S, Daniel F. Geosynchronous Large Debris Reorbiter: Challenges and Prospects[J]. The Journal of the Astronautical Sciences, 2012, 59(1):161-176.

[11] Huang J, Chuanjiang L, Guangfu M, et al. Coulomb Control of a Triangular Three-Body Satellite Formation Using Nonlinear Model Predictive Method[C]. Proceedings of the 33rd Chinese Control Conference, Nanjing, China, July , 2014, 28-30.

[12] Shuquan W, Hanspeter S. One-Dimensional Constrained Coulomb Structure Control with Charge Saturations[J]. IEEE Transactions on Aerospace and Electronic Systems. 2012, 48(1): 3-15.

[13] Gordon G, Lyon B, Hanspeter S. Steered Spacecraft Deployment Using Interspacecraft Coulomb Forces[C]. Proceedings of the 2006 American Control Conference Minneapolis, Minnesota, USA, June , 2006, 14-16.

[14] Saaj C, Lappas V, Schaub H, et al. Hybrid Propulsion System for Formation Flying Using Electrostatic Forces [J]. Aerospace Science and Technology, 2010, 14(5): 348-355.

[15] 张天平. 国外电推进技术进展综述[C]. 第二届中国电推进技术学术研讨会论文集, 2006, 8: 178-182. (Zhang Tianping. Airship Aero-dynamic Semi-empirical Model and Its Parameters Identification [C]. The second China Electric Propulsion Technology Symposium, Hangzhou, May 2007, 17-22.)

[16] Eric J．Pencil and Hani Kamhawi, et al．Evaluation of Alternate Propellant for Pulsed Plasma Thrusters[C]. IEPC, 1 47.

[17] Francis M, Todd T Peterson, et al. Pulsed Plasma Thruster Technology Directions[C]. AIAA paper, 2009, 97-2926.

[18] Berryman J, Schaub H. Analytical Charge Analysis for 2- and 3-Craft Coulomb Formations [C]. AAS/AIAA Astrodynamics Specialist Conference, Lake Tahoe, CA, August 7-11, 2005, AAS-05-278.

[19] Wang T, Xia G, Zhao N. Analysis and Control of Equal Mass Five-Craft Coulomb Formations Flying [J]. Trans. Japan Soc. Aero. Space Sci, 2016, 59(2):81-90.

[20] Wang T, Xia G, Zhao N. Reconfiguration and Control of Non-Equal Mass Three-Craft Coulomb Formation [J]. Journal of the Astronaut Sci. 2016，62(6):1-13.

[21] 王婷，张羽飞.等质量立体五星库伦编队的分析和控制 [J].宇航学报,2015, 36(11): 1279-1288. (Wang T, Zhang Y F. Analysis and Control for Three Dimensional Five-satellite Coulomb Formation Flight in Geostationary Earth Orbit[J]. Journal of Astronautica,2015, 36(11): 1279-1288.)

[22] 王婷，夏广庆，兰聪超. 粒子群算法求解不等质量库仑卫星编队最优构型[J].系统工程与电子技术，2016，38(2)：305-313. (Wang Ting, Xia Guangqing, Lan Congchao. Optimal Static Configuration of Non-equal Mass Coulomb Formation Satellites by PSO [J] . Journal of Systems Engineering and Elecreonics，2016，38(2)：305-313.)

Study of Coulomb Satellites Formation Reconfiguration by Hybrid Propulsion

Wang Ting

College of Electrical Engineering and Control Science, Nanjing Tech University, Nanjing 211816, China

ThehybridpropulsionwhichconsistsofCoulombforceandelectricpropulsionisproposedtoachievethereconfigurationcontrolofCoulombsatelliteformationduringcollisionavoidanceprocess.Inaddition,fuzzyLQRcontrolisappliedtoreconfigurationcontrolbysimulations.

Hybridpropulsion; Coulombsatelliteformation；Obstacleavoidance；Reconfigurationcontrol

2016-11-30

王 婷 (1981-)，女，山西人，博士，讲师，主要研究方向为卫星编队控制和机器人编队控制。

V448.21

A

1006-3242(2017)02-0020-05