基于最大能量熵的小波阈值去噪法研究

张鑫

（商洛学院电子信息与电气工程学院，陕西商洛726000）

基于最大能量熵的小波阈值去噪法研究

张鑫

（商洛学院电子信息与电气工程学院，陕西商洛726000）

分析了现有的软阈值、硬阈值以及软硬折衷阈值三种小波阈值去噪方法的优缺点，在此基础上，提出了一种基于最大能量熵的小波阈值去噪方法，根据最大能量熵的理论确定了改进型阈值函数中的加权因子。用三种阈值函数分别对Blocks、Bumps、Droppler信号进行滤波处理中，结果表明，基于最大能量熵的小波阈值去噪方法各项性能指标均优于另外两种方法，具有良好的去噪效果。

小波去噪；阈值函数；最大能量熵

在实际应用中采集到的信号都多多少少的的包含有一定的噪声，而噪声在一定程度上掩盖了信号本身的特征，使信号产生变异，所以去噪滤波就很有必要。1990年以来，小波理论被大量的研究，随着小波理论渐渐趋于完善，被广泛的应用于信号处理方面。小波去噪有三种方法：第一种是利用小波变换模极大值原理去噪，第二种是根据相邻尺度间小波系数的相关性取舍，再重构信号，第三种就是小波阈值去噪。前两种方法的计算量比较大，小波阈值去噪由于相对简单，计算量不大，视觉效果良好被广泛应用[1-2]。文献[3]利用阈值函数去改变小波的分解系数来进行去噪，但是计算量较大；文献[4-5]提出了一个阈值函数，该函数和均方差函数近似，利用该方法可以得到均方差意义下的最优值，但是该方法不能仅仅用均方差作为性能指标来进行评价。小波去噪的核心问题是如何选取合适的阈值函数。提出了一种基于最大能量熵的小波阈值去噪方法，根据最大能量熵的理论确定了改进型阈值函数中的加权因子。用三种阈值函数分别对Blocks、Bumps、Droppler信号进行滤波处理并用信噪比（SNR），均方根误差（RMSE），降噪后信号与滤波前信号的能量比例（ET）来考察对含噪信号去噪方面的效果。

1 小波阈值去噪

小波变换被认为能够集中能量，也就是说，一方面噪声信号因为本身能量谱比较分散、频率也比较分散，因此其小波系数比较分散且绝对值相对比较小；另一方面有用信号的能量会汇集在很少的小波系数上，这些小波系数通常绝对值比较大。对信号进行小波变换可以得到小波系数，通过对这些系数与设定的阈值进行比较，如果这些子空间的小波系数小于该阈值，则认为它是噪声信号，将其变为0，再进行重构就可以获得去噪后的信号。这就是阈值去噪的基本原理。小波滤波的核心问题是如何选取合适的阈值函数，进而计算出可以还原良好去噪信号所需的小波系数。因此，如何确定阈值是一个非常关键的问题。

小波去噪的阈值函数主要有3种：

1）软阈值函数[6-8]：假设信号f(t)进行小波分解后的小波系数为ωj，k，比较阈值λ和ωj，k，如果ωj，k的绝对值大于λ，那么小波系数ωj，k此时应为ωj，k的绝对值减去阈值λ的差，并保持符号不变；幅值小于或者等于λ的点变为0。

滤波器表达式为：

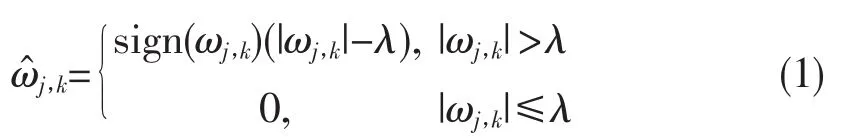
2）硬阈值函数：假设信号f(t)进行小波分解后的小波系数为ωj，k，比较阈值λ和ωj，k，如果ωj，k的绝对值大于λ，那么小波系数ωj，k此时不变，否则小波系数ωj，k置0。

滤波器表达式为：

3）软硬折衷阈值

1995年，在硬阈值和软阈值函数的基础上，Bruce和Gao Hong Ye研究出了一种软硬折衷函数[9]，以提高采集信号的信噪比（SNR）和减小均方误差（MSR）。具体的软硬折衷函数为：

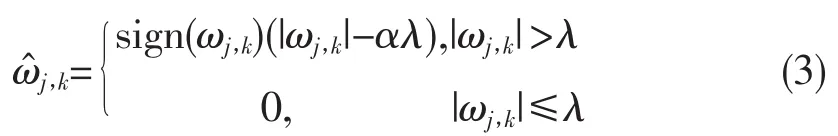
其中，α∈[0,1]为1个可变量。要注意的是，当α=1时该函数为软阈值函数；而当α=0时，该函数则与硬阈值函数相同。如图1所示，图1中的α=0.5。在实际工程中，一般从实际情况出发，然后再根据经验反复尝试来确定待定参数α的值。

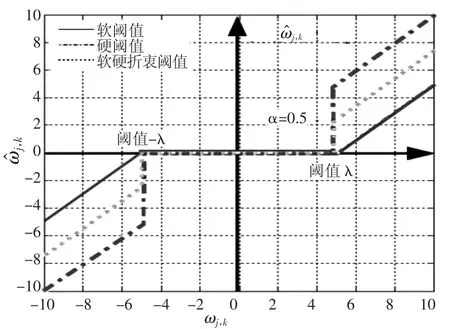
图1 软硬折衷阈值法

2 阈值函数的改进

对传统的软、硬阈值函数进行分析，发现硬阈值函数不是连续的，和硬阈值函数相比软阈值函数是连续的，然而它并不是任意阶连续可导。当今被提出的大部分去噪函数，去噪效果良好但是它们大部分都含有待定参数，而要确定这个参数一般需要通过大量的尝试和经验来确定，工作量较大。基于信号的小波能量熵理论，提出了基于最大能量熵的小波阈值去噪法。分解原始信号，可以得到噪声系数和高频系数，让它们的小波能量熵之和为最大，得到了最优的小波阈值去噪函数。

2.1 最大熵原理

最大信息熵[10]原理是Jaynes提出的，它的基本思想是，求满足某些约束的信源事件概率分布时，应使得信源的熵最大。由最大信息熵理论可以知道，噪声信号ε与真实信号g的相关性越小，它们的熵相加的结果就会越大。所以，对于去噪后得到的真实信号g，应该使噪声信号ε的信号熵与g的信号熵相加最大，此时应为最佳的去噪效果。

2.2 小波能量熵

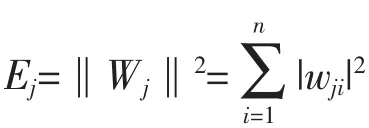
2.3 最优阈值的选取

去噪时，噪声信号和真实信号之间的相关性越小越好，也就是说对于去噪后得到的真实信号，应该使噪声信号的信号熵与它的信号熵相加结果最大，这样得到的就是最佳的阈值函数。

阈值处理后原始信号的高频小波系数为：

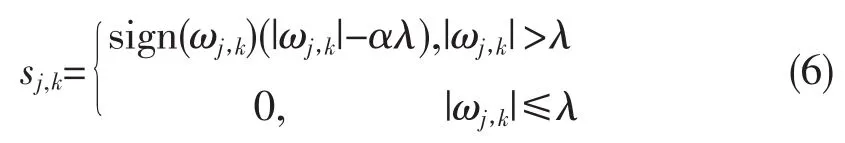
滤掉的噪声的高频小波系数为：

则信号部分的小波能量熵为：

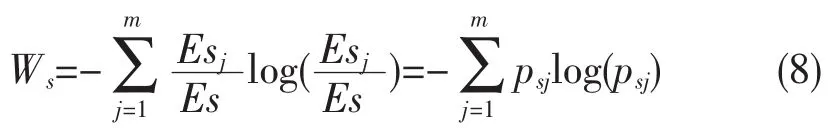
噪声部分的小波能量熵为：

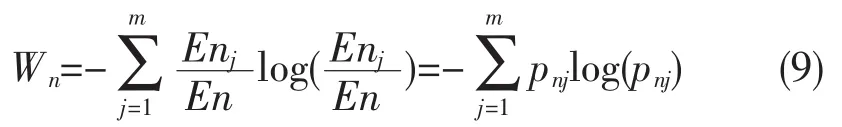
令W=Ws+Wn，W可表达为调整参数α的线性函数。

3 算法步骤

改进算法的步骤如下：

1）对噪声信号选择小波和分解层数进行多尺度分解，得到各层高频小波系数和最后一层的低频小波系数。

2）调整参数α先取0。

3）根据式(6)和式(7)，取得相应的处理后的小波系数sj,k和nj,k。

4）对利用式(8)和式(9)计算相应的小波能量熵Ws和Wn，求出两者之和W。

5）回到步骤2），调整参数α递增0.01或者0.05，再次计算W。当W取最大值时，此时的α的是最佳参数，此时得到最优阈值，所用的阈值函数所得到的滤波效果最佳。

4 仿真实验与分析

为了验证此方法的效果，采用Matlab平台用3种阈值滤波法对Blocks、Bumps、Droppler信号实行仿真实验。仿真信号均加入高斯白噪声，噪声信号服从N(0,1)，再用“db4”小波对带噪声信号进行3层分解，分别利用软、硬阈值函数和新的阈值折衷函数（用分层阈值）对分解后的小波系数进行小波阈值滤波，用信噪比（SNR），均方根误差（RMSE），降噪后信号与滤波前信号的能量比例（ET）来考察对含噪信号去噪方面的效果。

4.1 Bumps信号滤波仿真

如图2所示，当α=0.8时，Bumps信号的小波熵最大，此时得到最佳阈值函数。从图3中可以看出，软阈值在横坐标0～200部分无法保留信号的原始特征。硬阈值去噪信号在横坐标200和950处出现了伪Gibbs现象。而本文方法很好的避免了这一现象的发生。表1为不同阈值函数对Bumps信号的滤波性能评价结果，软阈值法的信噪比为12.5944，硬阈值法的信噪比15.5868，均低于本文的方法，且该方法得到的均方根误差也是最小的，在能量比例上最大，说明保留了最多原信号的能量特征。

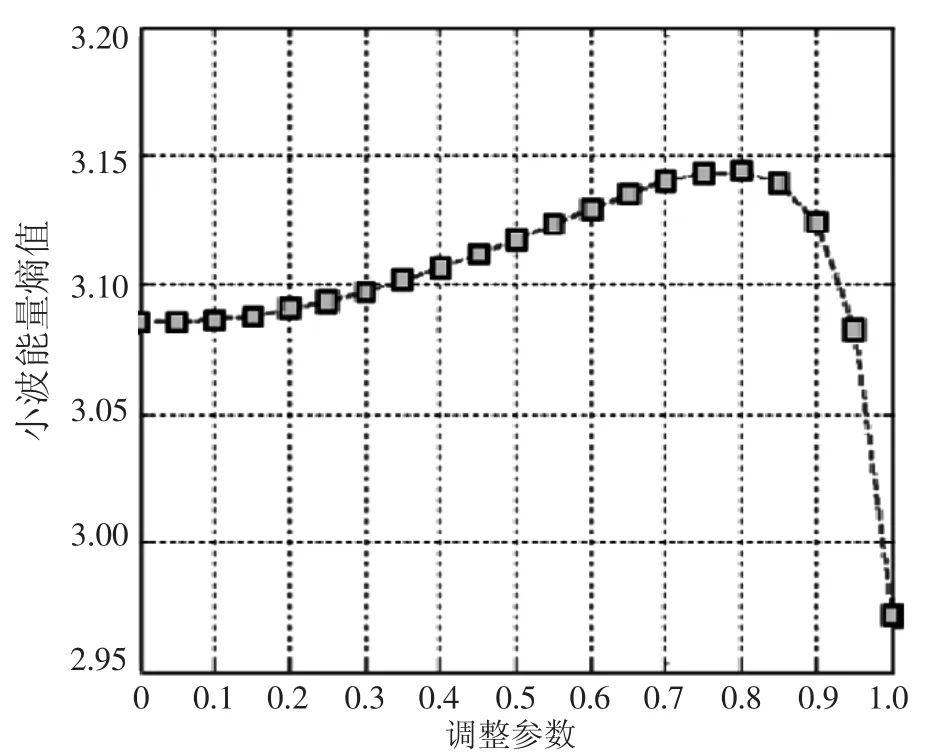
图2 Bumps信号调整参数与小波能量熵的关系

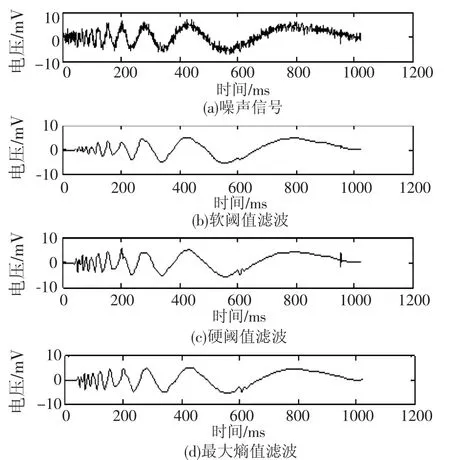
图3 Bumps信号三种滤波方法比较

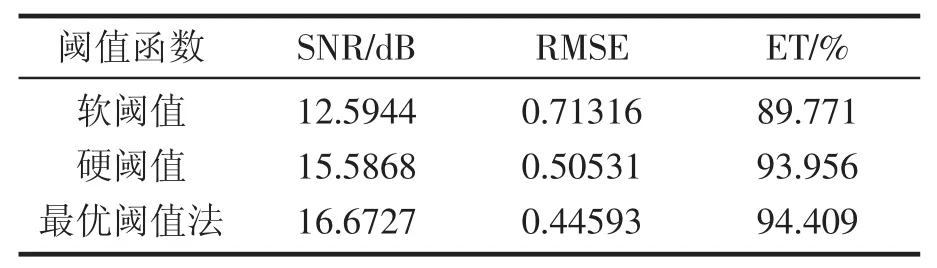
表1 Bumps信号在不同阈值函数下的滤波性能评价标准

4.2 Blocks信号滤波仿真

由图4可知，α为0.5时，小波熵最大。由图5可知，软阈值法滤波结果看起来比较平滑，然而由于Blocks信号的详细部分有很多都被省略，不能精准的表现出信号的局部特征，发生了显著的失真现象，SNR为14.9074，RMSE为1.0775，ET为95.072%，与其他两种方法相比较不能很好的抑制噪声，保留的原信号特征也最少，去噪结果不是很好；硬阈值法的SNR为18.5569，RMSE为0.70782，ET为98.415%，能较好的抑制噪声信号且较多的保留了原信号特征，但是在横坐标800处有显眼的伪Gibbs现象，且局部剧烈振荡，结果不够平滑；而基于最大能量熵的小波阈值去噪法SNR为20.7592，RMSE为0.69153，ET为99.842%，信噪比最高且基本完全保留了原信号的特征，所以与干净的Blocks信号更加接近。表2显示基于最大能量熵的方法各项性能均优于其他两种方法。

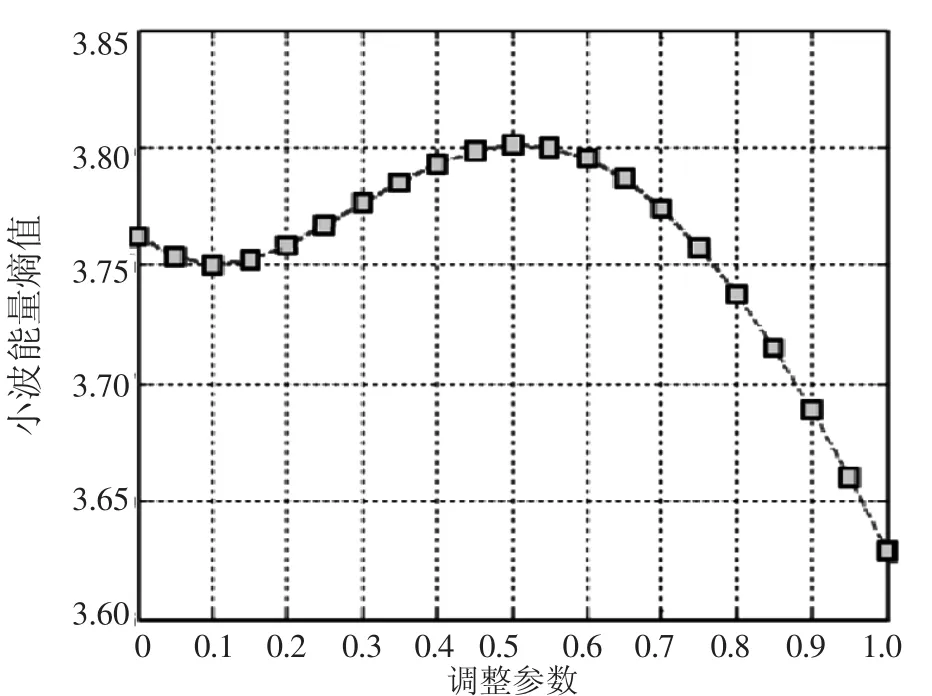
图4 Blocks信号调整参数与小波能量熵的关系

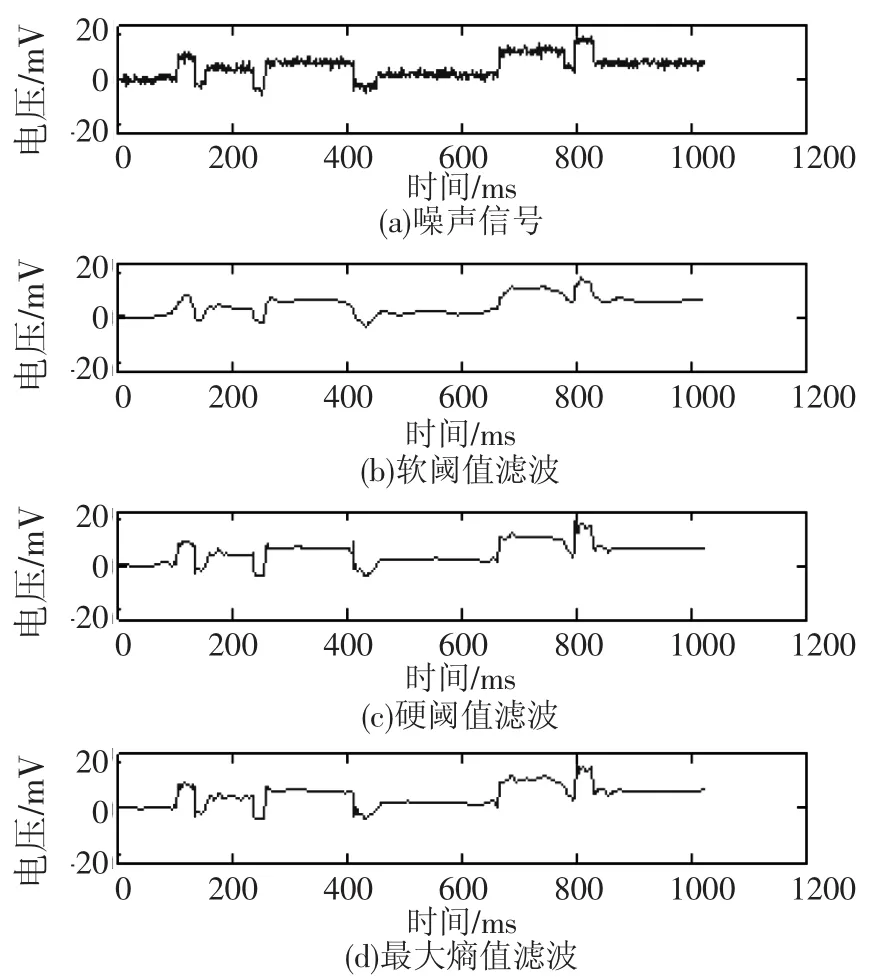
图5 Blocks信号三种滤波方法比较

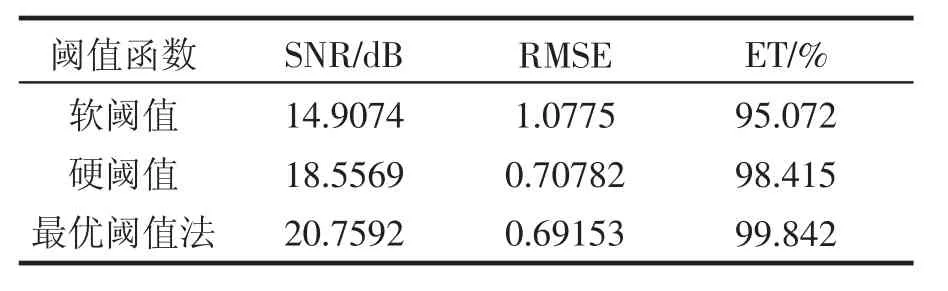
表2 Blocks信号在不同阈值函数下的滤波性能评价标准

4.3 Droppler信号滤波仿真

由图6可知，α为0.85时，Droppler信号的小波熵最大。由图7从视觉上看三种方法差距不大，采用文中的阈值去噪方法，滤波后的波形细节上更加光滑，更加平直。从表3可以看出，基于最大能量熵的小波阈值去噪法的信噪比最高，均方差最小，能量比例最大，优于其他两种方法。

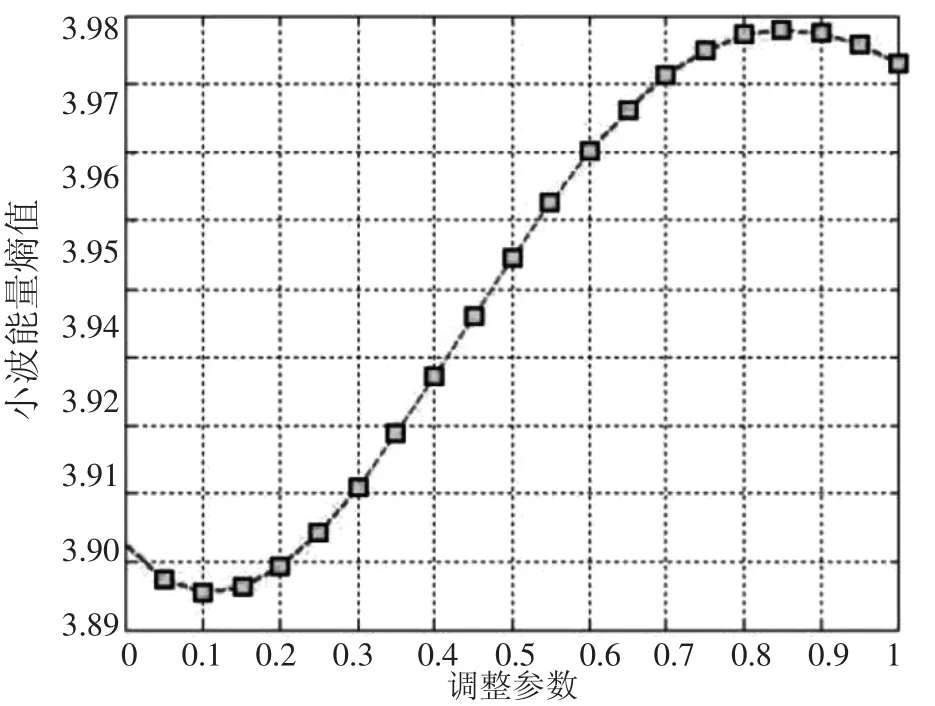
图6 Droppler信号调整参数与小波能量熵的关系

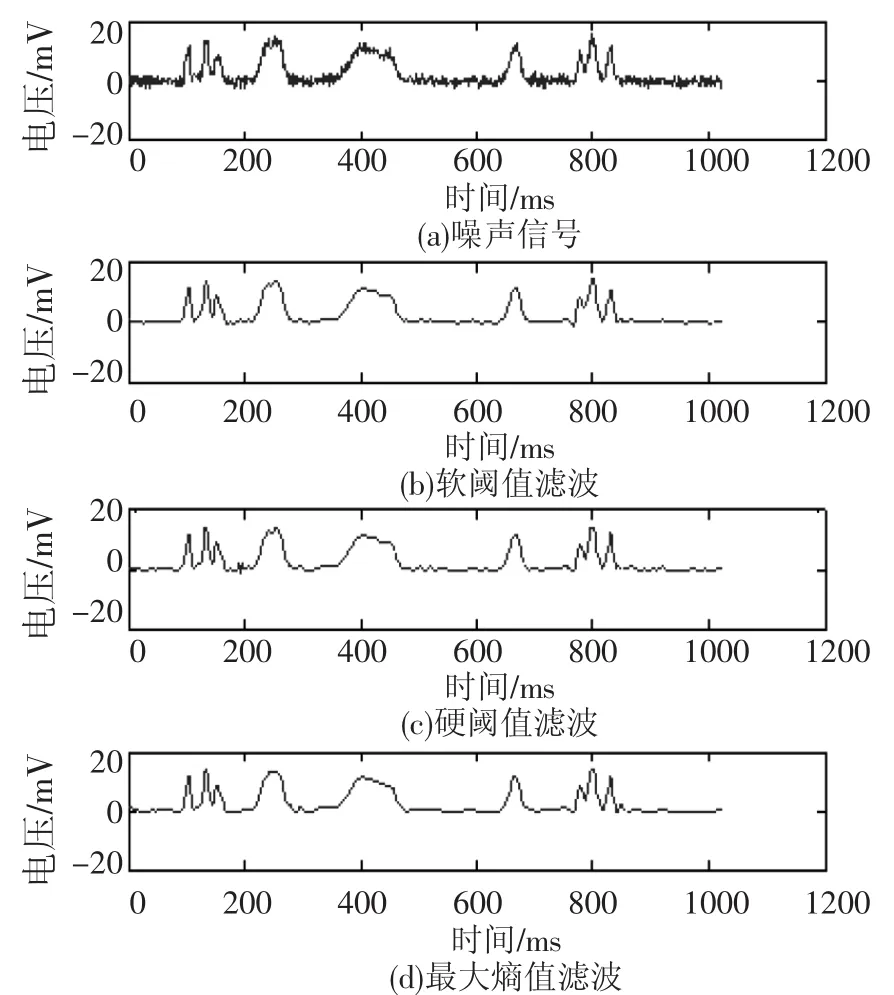
图7 Droppler信号三种滤波方法比较

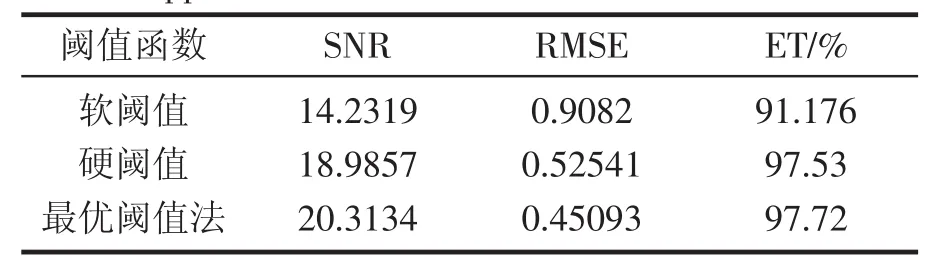
表3 Droppler信号在不同阈值函数下的滤波性能评价标准

5 结论

小波去噪的核心问题是如何选取合适的阈值函数。分析了现有的软阈值、硬阈值以及软硬折衷阈值三种小波阈值去噪方法的优缺点，提出了一种基于最大能量熵的小波阈值去噪方法，首先对噪声信号选择小波和分解层数进行多尺度分解，得到各层高频小波系数和最后一层的低频小波系数，根据最大能量熵的理论确定了改进型阈值函数中的加权因子，此时得到最优阈值，阈值函数的滤波效果最佳。为了验证算法的有效性，用软阈值、硬阈值、改进阈值三种阈值函数分别对Blocks、Bumps、Droppler信号进行了去噪处理。结果表明，基于最大能量熵的小波阈值去噪法降噪后信号与滤波前信号的能量比例最高，均方差最小，信噪比最高，具有良好的去噪效果。

[1]陈晓曦,王延杰,刘恋.小波阈值去噪法的深入研究[J].激光与红外,2012,42(1)：105-110.

[2]王荣.一种新的基于闪烁噪声的扩展目标跟踪方法[J].商洛学院学报，2016,30(2)：19-24.

[3]DONOH D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3)：613-627.

[4]PAN Q,ZANG L,DAI G Z,et al.Two denoising methods by wavelet transform[J].IEEE Transactions on Signal Processing,1999,47(12)：3401-3406.

[5]潘泉,孟晋丽,张磊,等.小波滤波方法及应用[J].电子与信息学报,2007,29(1)：236-242.

[6]杨恢先,王绪四,谢鹏鹤,等.改进阈值与尺度间相关的小波红外图像去噪[J].自动化学报,2011,37(10)：1167-1174.

[7]高洪玉,裴连群.双树复小波域农业图像改进半软半硬阈值函数去噪[J].江苏农业科学,2015,43(9)：450-452.

[8]张金榜,孙艺笑,王润典,等.改进的阈值函数去噪算法[J].电子科技,2014,27(02)：17-20,24.

[9]兰超,欧阳林子.一种基于改进的软硬阈值折衷法的去噪研究[J].科学技术与工程,2009,9(18)：5515-5517,5526.

[10]郑加苏.基于图像信息熵的无参考图像质量评估算法的研究[D].北京：北京交通大学,2015：5-78.

（责任编辑：李堆淑）

Research on Wavelet Threshold Denoising Algorithm Based on Maximum Energy Entropy

ZHANG Xin
(School of Electronic Information and Electrical Engineering,Shangluo University,Shangluo726000,Shaanxi)

Wavelet denoising of the soft thresholds,hard thresholds and soft and hard tradeoff thresholdsare andlyzed,and a wavelet threshold denoising method based on maximum energy entropy is proposed.Based on the maximum energy entropy The weighting factor in the improved threshold function is determined.According to the theory of maximum energy entropy,the weighting factor in the improved threshold function is determined.Blocks,Bumps and Droppler signals are filtered by three threshold functions.The results show that the performance of using wavelet threshold denoising method based on maximum energy entropy is superior to the other two methods,and has good denoising effect.

wavelet denoising;threshold function;maximum energy entropy

TP911.7

：A

：1674-0033（2017）04-0023-05

10.13440/j.slxy.1674-0033.2017.04.006

2017-04-16

商洛学院科研基金项目（16SKY-FWDF005）

张鑫，女，陕西商州人，硕士，助教