改进型Mean-Shift算法在行人目标跟踪中的应用

李亚文，王博

（商洛学院电子信息与电气工程学院，陕西商洛726000）

改进型Mean-Shift算法在行人目标跟踪中的应用

李亚文，王博

（商洛学院电子信息与电气工程学院，陕西商洛726000）

针对传统Mean-Sshift算法对于运动目标特征变化较快、某些干扰和遮挡等问题而引起目标定位偏差的情况，提出了一种基于改进型的颜色直方图的Mean-Shift算法，该算法是将颜色直方图和三重帧间差分的方法相结合的一种目标跟踪算法。实验结果表明，应用改进后的算法思想，可以较准确的对视频流中的行人目标进行实时跟踪，新算法能较好的解决运动目标特征变化较快而引起跟踪不准确的问题，实现对行人目标进行准确定位跟踪。

Mean-Shift算法；颜色直方图；目标跟踪；核函数

随着交通安全和人居环境等情况的不断复杂，视频监控技术已经广泛应用于城市道路、地铁、小区安防，银行监控等领域，视频监控技术只要实现对感兴趣运动目标进行检测、跟踪、识别和行为理解等4个步骤[1]，实现对视频中的运动目标运动估测。其中运动目标的跟踪技术是视频监控技术的关键，检测出感兴趣的运动目标后，进行特征提取、模型建立，并不断地更新运动目标的位置信息，实现对运动目标的跟踪。

在20世纪90年代，视频中的运动目标跟踪技术得到了快速发展，其中具有代表性的包括：Condensation算法，粒子滤波算法、Kalman滤波算法和Mean Shift等算法[2-4]，我国视频检测跟踪技术起步较晚，但也取得了一些成果，李源[5]提出了一种层级粒子滤波的跟踪方法，中科院北京自动化研究所对行人的运动跟踪、城市交通状况的视觉监控等方面都进行了深入的研究，并取得了一定的研究成果；此外，国防科技大学、电子科技大学、西安电子科技大学等也对视频监控中的目标跟踪技术做了大量研究，取得了一批研究成果。

目前常见的目标跟踪算法主要包括5种：区域的跟踪、活动轮廓的跟踪、模型的跟踪、特征的跟踪和机器学习的跟踪[6]等，而Mean-Shift算法就是基于模型的运动目标跟踪算法，由于其运算量较好，迭代次数较少，定位准确，因此在运动目标跟踪中得到了广泛的应用，传统的Mean-Shift算法对于运动目标较快，背景变化复杂的物体很难进行跟踪，因此，为了实时跟踪运动状态变化较快的目标，本文提出了一种改进型的颜色直方图的Mean-Shift算法，该算法是一种颜色直方图和三重帧间差分相结合的行人目标检测算法，并在实验中进行了算法实现。

1 Mean-Shift算法原理

设二维实数空间中有样本点则位于点的向量定义[7]为：

式(1)中，是以xi为原点，x为半径的球形区域内的点的集合，该集合可以表示为式(2)。

其中，h是偏移向量，即落入半径为x的区域内的样本点的数目，也是样本点对应于点的偏移向量求和后的平均向量。如图1箭头所示，Mean-Shift向量的方向是样本分布较多的方向，图1中，偏移向量用箭头线段表示，整个区域的范围用大圆圈表示，小圆圈内的黑点表示基准点，而小圆圈表示样本点，且基准点朝着样本分布最多的方向。

图1 Mean-Shift向量指示图

设d维欧式空间中存在点x，用列向量表示x的模：||x||2=XTx，若函数K的剖面函数为k，k∈[0，∞]，则核函数[7-8]可以用式(3)表示，其剖面函数在有限区间内是连续且非增的函数。

由于受到到原点距离不同的影响，每个样本点重要性不一样，因此引入了权重系数的概念，基本的向量扩展[9]如式(4)所示：

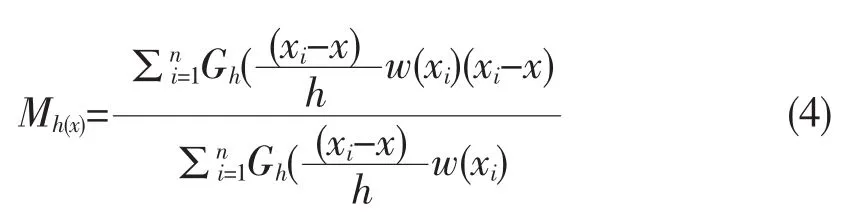
在式(4)中，w(xi）是赋给采样点的权重系数，Gh(x)是半径为h的单位核函数。假设在d维空间中存在n个采样点xi(i=1，…，n)，则概率密度函数f(hx)的核函数估计为：

其中W(xi)是赋给采样点xi(i=1，…，n)的权重系数，k(x)是核函数K(x)的剖面函数，它们之间的关系可以表示为：

g(x)是k(x)的负导函数，即，g(x)=-k′(x)是核函数为G(x)的剖面函数，即：

f(x)的梯度[10]为：

代入g(x)和G(x)函数,则概率密度函数梯度又可以表示为：

在式(9)中，Mh(x)是Mean-Shift向量，fG(x)是以G(x)为核函数的概率密度函数[11-12]，这样，得到Mh(x)为：

从式（10）中可以看出，概率密度增加的最大的方向即Mh(x)的指向，通过核函数G(x)在x点计算就可以得到Mean-Shift，向量Mh(x)跟与核函数K(x)估计的概率密度函数f(x)的梯度之间是正比例关系，Mean-Shift算法也就是迭代的步骤[13]，变换Mh(x)为：

在初始点x给定时，G(x)为核函数，容许的最小误差就是ε，那么Mean-Shift算法歩骤可以表示3步：

Step1：计算m(x)；

Step2：将m(x)值赋给x；

Step3：如果满足||m(x)-x||＜ε，跳出循环，若不满足，则继续执行Step1。

Mean-Shift算法的3步实现步骤都是不断地移向概率密度梯度方向，直到歩长||m(x)-x||＜ε时，移动才会结束，跳出循环，这个时候Mean-Shift算法收敛达到概率密度的最高点，歩长的大小与密度成反比关系。

2 改进型的颜色直方图模型的Mean-Shift算法

2.1 算法思想

本文提出基于颜色直方图模型的Mean-Shift算法，该算法是一种将颜色直方图和三重帧间差分的方法相结合的行人目标跟踪算法，行人目标建模是通过RGB颜色空间中的颜色直方图来完成的。所建立的目标模板一般是由一个规则的闭合线条所包围的子图来确定。减少计算量就需要将每个通道的灰度值量化到M区间中。量化后的特征值取值范围可以用U=1，…，N来表示，子图像素信息可抽象为{xi*}，i=1，…，n来表示。可以用式(12)来表示目标模型[13-14]：

在式(12)中，h代表的是带宽函数，是跟踪框大小的二分之一。k(xi)可以通过弱化边缘像素，增强算法的抗遮挡能力，从而突出中心像素，在一定程度上，可以抑制由于背景变换较快而引起的跟踪误差。目标模型的概率密度分布用q表示，qu表示q的第u特征分量的概率密度，δ具有判断b(xi*)所属特征区间的作用。C为标准化常量系数使，因此。

在后续几帧中目标可能出现的候选区域的内容可抽象为nh个像素点，用{xi}，i=1，…，nk表示，用y表示其中心位置。那么候选目标模板的概率可以用核函数直方图分布来表示为：

ρ的取值范围是由0到1之间，候选模型与目标模型越是相似度越高，ρ的值也就越大，在有限步骤求得合适的y使得ρ(y)值最大计算ρ(y)在y0处的泰勒级数展开式，能够得到：

在式(15)中可以看到，该子项表示在当前图像中y点处核函数的密度估计，并通过{xi}，i=1，…，nh进行了加权。只要最大化式（15）中的第二项就可以使得p(y)变得最大，所以这个问题转化为求解wi表示的核密度估计函数的问题。在求解过程中，核函数逐步递归会向y1移动：其中核函数选择了Epanechnikov核，所以y1可以表示为：

根据分析的算法思想，提出的改进型的颜色直方图模型的Mean-Shift算法实现流程（见图2）。

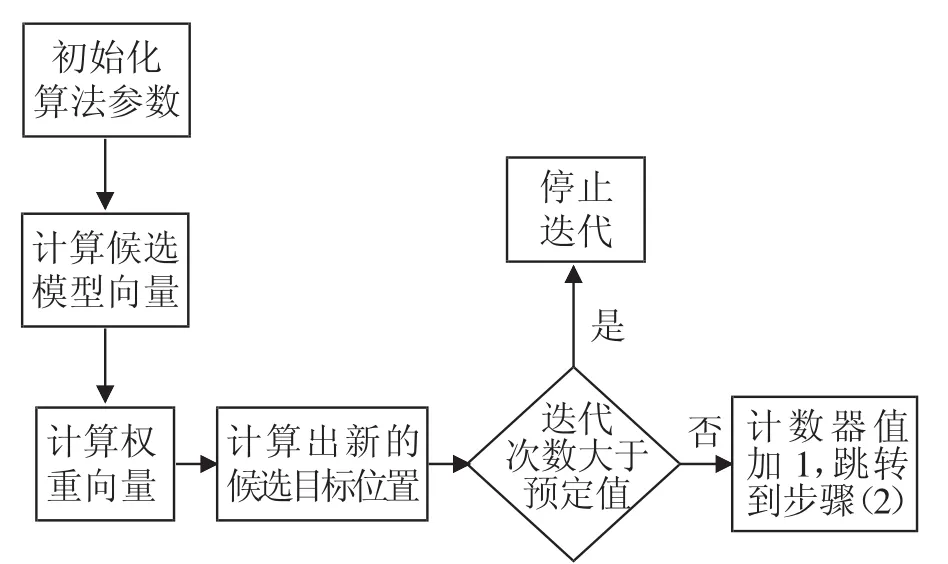
图2 改进型的颜色直方图模型的Mean-Shift算法流程图

2.2 改进型的Mean-Shift算法在运动目标跟踪中的应用

该算法主要可以应用于监控视频包括交通安全、小区安防、居家安全、ATM监控等视频流中对行人的跟踪，具体的实现过程如图3所示，主要包括5步完成。

图3 视频流中行人目标的跟踪

1）首先输入视频文件解开为多帧图像序列，判断是否为首帧图像，如果是，则提取首帧图像进行灰度化处理、膨胀腐蚀模板设置和阈值设置等相关的初始化操作。

2）如果不是首帧图像，则先对图像进行合理的背景建模。包括背景差分、二值化、形态学处理、前景轮廓检测等操作。对运动区域进行检测和提取所采用的方法是改进三帧差分算法。

3）从待检测候选区域提取的有效运动区域进行检测，采用SVM分类器进行判断。这样可以较为精确的定位行人目标的运动信息，包括大小、速度等。

4）当运动目标进行有效候选待测区域，就对其进行基于改进型的Mean-Shift的行人跟踪算法，用矩形框框出行人目标，并进行实时跟踪。当行人目标离开有效检测区域后就会产生计数，并输出目标跟踪的矩形跟踪结果。

5）重复上述步骤2）至步骤4）一直判断、跟踪、计数，直到判断是否为末帧，如果为末帧，就可以结束程序了，如果不是末帧，那么就返回到步骤2），继续执行各个步骤。

3 实验仿真与结果分析

3.1 传统的Mean-Shift的行人跟踪

实验中对现有的一段室内羽毛球馆的视频进行分析，将18 s的视频文件解开为511帧图像，应用传统的Mean-Shift的算法对室内羽毛球馆的一个运动员进行实时行为跟踪，如图4所示，提取第4帧、第15帧和第46帧，实验结果表明，传统的Mean-Shift算法对于目标运动特征变换缓慢时可以实现对蓝色服装的运动员的准确跟踪与定位，然而，当运动员进入比赛状态后，运动速度比较快时，传统的Mean-Shift算法已经不能对目标进行跟踪了，如图5所示，对视频流中的第115帧、第222帧和第464帧进行目标跟踪时，矩形框内已将不能准确跟踪蓝色服装的运动员的运动情况。

图4 传统Mean-Shift的行人跟踪

图5 目标变化较快时的跟踪

3.2 改进型Mean-Shift的行人跟踪

实验环境为Matlab2014（a），对录制的一段监控视频流进行实验，应用本文提出的基于颜色直方图模型的Mean-Shift算法对视频流中的行人进行跟踪。这里选取的是RGB颜色空间，核函数釆用Epanechnikov核。在实验中，对视频流中运动着的行人进行了全程跟踪。将采集的监控视频move.avi，解开为298帧图像，实验中任意选取视频流中的第1、13帧图像，进行行人目标跟踪，如图6(c)，图7(a)所示。其中在第1帧中手动选取了一个矩形框，这个矩形框包含了所有的行人目标的具体特征，主要包括目标的大小、运动的方向和速度的大小等，将该矩形框所包含的行人目标的特征信息作为跟踪模板，在后续的多帧图像中以此模板为基础进行特征信息的更新，实现对运动目标的跟踪。由于行人在运动过程中，外界环境变换较少，主要是运动中的行人胳膊，腿的不断变化，应用颜色特征具有旋转不变的特性，可以较准确的跟踪行人的运动轨迹。如图6(c)，图7(a)所示分别为对第1帧和第13帧中行人的跟踪情况，并对视频流中的不连续图像帧第78帧和第106帧中的行人运动进行了跟踪，如图7中(b)、(c)所示，应用改进的直方图模型的Mean-Shift算法，可以实现对视频流中的行人运动目标进行清晰、准确的跟踪。

图6 原视频流中的图像帧

图7 行人运动目标跟踪

4 结语

行人跟踪相比车辆等形状固定的物体跟踪来说具有复杂性，主要表现在行人的运动速度大小不定，周围环境复杂多变等，这些不定因素的存在都使得行人目标跟踪的难度有所加大。针对传统Mean-Shift算法对于运动目标特征变化较快、某些干扰和遮挡等问题而引起目标定位偏差的情况，本文在综合各种算法的优缺点的基础上，提出了一种基于改进型的颜色直方图的Mean-Shift算法，改进型的算法是将颜色直方图和三重帧间差分的方法相结合的行人目标跟踪算法。通过对录制一段视频流进行行人目标跟踪，基于颜色直方图的Mean-Shift算法应用Epanechnikov核作为核函数，通过建立候选模型向量，计算模型权重，确定候选模型目标位置，送入SVM分类器进行判断，对有效检测区域的行人目标进行准确跟踪，实验结果表明，该算法能较好的跟踪行人的运动轨迹，即使在行人目标运动变化时，依然能准确的锁定运动目标，实现准确定位与跟踪。

[1]杨辉,刘军,阮松,等.基于Mean-Shift算法视频跟踪研究[J].计算机工程与设计,2013,34(6)：2062-2066.

[2]邹青志,黄山.一种基于Mean-Shift的快速跟踪算法[J].计算机科学,2017,44(3)：278-282.

[3]张赛钰,朱小玲,汪衍广,等.基于帧差法与Mean-shift算法相结合的运动熔滴识别与跟踪方法[J].上海交通大学学报,2016,50(10)：1605-1608.

[4]郑鹏.基于改进Mean-shift算法的目标跟踪技术研究[D].郑州：华北水利水电大学,2015：6-8.

[5]梁新华,潘泉,杨峰,等.基于两级采样的粒子滤波检测前跟踪算法[J].系统工程与电子技术,2011,33(9)：1921-1926.

[6]刘晴,唐林波,赵保军,等.改进的Mean-shift目标跟踪算法[J].系统工程与电子技术,2013,35(6)：1318-1323.

[7]武海巍,于海业,田彦涛,等.基于核函数与可见光光谱的大豆植株群体净光合速率预测模型[J].光谱学与光谱分析,2016,36(6)：1831-1836.

[8]李华亮,钱志鸿,田洪亮,等.基于核函数特征提取的室内定位算法研究[J].通信学报,2017,38(1)：158-167.

[9]汪海燕,黎建辉,杨风雷,等.支持向量机理论及算法研究综述[J].计算机应用研究,2014,31(5)：1281-1286.

[10]郭明玮,赵宇宙,项俊平,等.基于支持向量机的目标检测算法综述[J].控制与决策,2014,29(2)：193-200.

[11]马正华,顾苏杭,戎海龙,等.基于SIFT特征匹配的CamShift运动目标跟踪算法[J].计算机科学,2014,41(6)：291-294,323.

[12]惠国保,童一飞,李东波,等.基于改进的图像局部区域相似度学习架构的图像特征匹配技术研究[J].计算机学报,2015,38(6)：1148-1161.

[13]尚明姝.基于改进SIFT特征匹配的快速图像拼接算法[J].微电子学与计算机,2014,31(1)：64-67.

[14]余旺盛,田孝华,侯志强,等.基于关键区域特征匹配的视觉跟踪算法[J].电子学报,2014,42(11)：2150-2156.

（责任编辑：李堆淑）

On Application of an Improved Mean-Shift Algorithm in Pedestrian Target Tracking

LI Ya-wen,WANG Bo
(School of Electronic Information and Electrical Engineering,Shangluo University,Shangluo726000,Shaanxi)

In traditional Mean-Shift algorithm,the target location has some deviation because of the rapidly changing characteristic,the disturbances and occlusion,therefore an advanced color histogram Mean-Shift algorithm is proposed,which combines the color histogram with the triple frame difference method.Simulation results show that the advanced new algorithm can track the pedestrian target accurately.In addition,it can avoid the problem of inaccurate location in the condition of quickly changing characteristics.

Mean-Shift algorithm;color histogram;target tracking；kernel function

TP273

：A

：1674-0033（2017）04-0010-05

10.13440/j.slxy.1674-0033.2017.04.003

2017-05-05

商洛学院科研基金项目（16SKY002）

李亚文，女，陕西华县人，硕士，讲师