基于半直觉模糊图的两种聚类分析算法

鱼先锋，万世昌

（商洛学院数学与计算机应用学院，陕西商洛726000）

基于半直觉模糊图的两种聚类分析算法

鱼先锋，万世昌

（商洛学院数学与计算机应用学院，陕西商洛726000）

给出了半直觉模糊图传递闭包和最大生成树的概念；提出了基于半直觉模糊图传递闭包和最大相关树的两种聚类分析算法。讨论了算法的合理性，分析了算法的复杂度。结合实例，用这两种聚类分析算法做了基于半直觉模糊图聚类分析。结果显示算法合理高效。

半直觉模糊图；传递闭包；最大生成树；聚类分析

图论将对象及对象间的联系抽象成图形，是分析解决实际问题的一种很有效的方法。如今图论作为重要的数学工具已广泛应用在计算机科学、信息论、控制论、系统科学等众多领域。经典图论只能用于刻画对象间的确定关系；而现实世界中对象间很多关系都是不确定的。Zadeh提出了模糊集[1]用以表示对象间不确定的隶属关系。Atanassov提出了直觉模糊集[2]，是对Zadeh模糊集最有影响的一种扩充和发展。Rosenfeid第一次提出了模糊图的概念。在提出了若干模糊图的相关概念及性质后，Rosenfeid初步建立了模糊图论系统。然后Mordeson等[3-7]结合已有的模糊图理论，给出了模糊图之间的关系、模糊图的补、模糊图的最优路、强树等相关的连通性质，以及其它性质及运算的研究；提出了完全模糊图和正则模糊图，及相应的运算性质。还有许多文献也研究了模糊图的相关性质与应用[8-10]。在文献[11]建立了半直觉模糊图模型，用顶点表示对象，用具有直觉模糊测度的边刻画对象之间的联系。给出了半直觉模糊图的生成子图、度、路径、相关截图、无犹豫半直觉模糊图及其序等概念。本文拟在文献[11]基础上给出半直觉模糊图传递闭包和最大相关树的概念，并在此基础上给出通过先求半直觉模糊图传递闭包和最大相关树再求其相关截图的方法来做聚类分析的两种聚类算法，并对算法的复杂度作以分析。最后将结合经典实例作基于半直觉模糊图的聚类分析。

1 半直觉模糊图的相关理论

定义1～定义3是在文献[11]中建立的半直觉模糊图模型及在本文中将要用到的相关概念。

定义1半直觉模糊图：半直觉模糊图为直觉模糊关系集其中，

1）V={v1，v2，…，vn}为顶点之集，表示有限个对象；

半直觉模糊图的边集是直觉模糊关系，可以表示成n×n(n=|V|)的一个直觉模糊矩阵，。这样以来半直觉模糊图就可以用来表示了。

定义2半直觉模糊图子图：设，为半直觉模糊图，

2）V1′，V2′⊂V，且V1′∩V2′=φ，称是的连通分量；

定义3半直觉模糊图的截图：设为一个半直觉模糊图，对∀p，q，0≤p，q≤1且p+q≤1，

定义4半直觉模糊图的性质：在半直觉模糊图中

一般对象间的相关性是相互的，即eij=(vi，vj)=eji所以半直觉模糊图的边集一般是一个对称关系，∀vi，vj∈V只定义无向边eij即可。另外∀vi∈V被认为每个对象与自身是完全相关的即eii=(vi，vi)=(1，0)。可见，一般的直觉模糊关系就是一个满足自反性和对称性的直觉模糊关系。就是直觉模糊相似矩阵[12]。

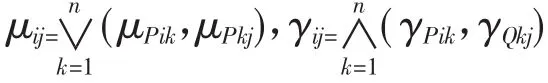
定义6直觉模糊关系的幂：为直觉模糊矩阵，定义的幂，其中m∈N+，并规定为n元直觉模糊单位阵。

定义7半直觉模糊图的传递闭包：设为半直觉模糊图，为直觉模糊关系的传递闭包，则称半直觉模糊图为的传递闭包。

定义8半直觉模糊图的序：为一个半直觉模糊图，，，若μ1=μ2且λ1=λ2，则称e1等于e2记作e1=e2；否则，

1）若d＞0则称e1相关大于或不相关小于e2记作e1≻e2。

2）若d＜0则称e1相关小于或不相关大于e2记作e1≺e2。

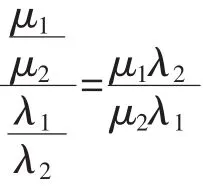
定义半直觉模糊图的序是为了求最大相关树时任意两条边可以排序。

定义9半直觉模糊图最大相关树：设为半直觉模糊图，若满足，

定义9是将经典图论中图的最小生成树的定义扩展到半直觉模糊图中。

2 基于半直觉模糊图的聚类分析

相似度和相异度是现实世界中对象间最主要的关联属性之一。将对象作为顶点集，将对象间的相似度作为相关度，相异度作为不相关度，就可以很自然的用半直觉模糊图刻画对象间的相似度和相异度。相似度和相异度主要应用是聚类分析、目标识别[12-17]。对象分类是研究对象属性和性质的最基本的一种方法。聚类分析的基本原理是定义对象间的相似度或相异度，然后将对象按相似度由大到小，或按相异度由小到大不断聚合到不同类型中。下面给出基于基于半直觉模糊图的两种聚类分析算法。

2.1 基于半直觉模糊图传递闭包的聚类分析算法

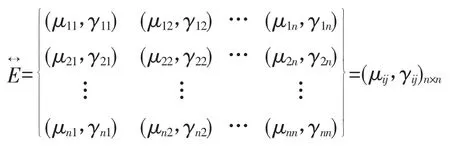
定理1在半直觉模糊图的传递闭包中，边集是一个等价直觉模糊关系。

定理1的证明见文献[15]。

定理2聚类分析结果一般包含多个连通分量，连通分量的个数为对象集V={v1，v2，…，vn}中所有对象在相关水平(p，q)下的分类类型数；在的同一连通分量中的顶点属于同一种类型。

定理3基于半直觉模糊图传递闭包图的聚类分析算法的空间复杂度为o(n3)，时间复杂度为o(n4)。

证明：算法的主要空间和时间开销来自于求半直觉模糊图传递闭包图。存储需要开辟n个规模为n×n的二维数组空间，故空间复杂度为o(n3)。根据定义5一次直觉模糊关系合成需要求n×n个直觉模糊数。求一个直觉模糊数要计算，需要做2n次max-min运算，所以一次直觉模糊关系合成的时间复杂度为o(n3)。而通常求直觉模糊传递闭包图要做n次直觉模糊关系合成求得，。

所以基于半直觉模糊图传递闭包图的聚类分析算法的时间复杂度为o(n4)。

2.2 基于半直觉模糊图最大相关树的聚类分析算法

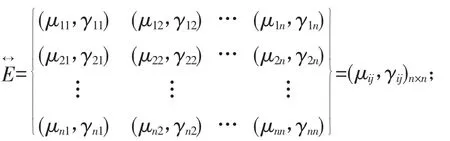
定理4基于半直觉模糊图最大生成树的聚类分析算法第2）步计算结果是的最大相关生成树。

基于半直觉模糊图最大生成树的聚类分析算法第2）步计算过程实际上是在Kruskal算法（经典图的最小生成树算法）基础上，稍加改动。区别一是对边排序是按定义3中给出的序关系比较大小的；二是最大生成树的边是按由大到小的顺序添加的。其他步骤算法基本原理是一样的。

定理5基于半直觉模糊图最大生成树的聚类分析结果一般包含多个连通分量，连通分量的个数为对象集V={v1，v2，…，vn}中所有对象在相关水平(p，q)下的分类类型数；在的同一连通分量中的顶点属于同一种类型。

定理6基于半直觉模糊图最大生成树的聚类分析算法的空间复杂度为o(n2)，时间复杂度为o(n2log2n)。

证明：算法的输入为半直觉模糊图；其顶点集和直觉模糊相似矩阵空间复杂度为o(n)和o(n2)。中间计算结果和算法最后输出结果都为初始半直觉模糊图的子图，空间复杂度不超过o(n2)；所以整个计算过程的空间复杂度为o(n2)。

用冒泡、选择、交换、插入排序法复杂度为o((n2)2)=o(n4)。其他计算的时间复杂度都与的规模相同为o(n2)。所以整个计算过程的时间复杂度为o(n2log2n)。

2.3 应用实例

某手机市场欲对5种不同的手机v1，v2，v3，v4，v5进行分类，每部手机有6个可供评价的因素：硬件功能(G1)，待机时间(G2)，价格(G3)，运行速度(G4)，设计外观(G5)，安全性(G6)．每部手机在各评价因素（属性）下的特征信息用直觉模糊数表示，见表1。

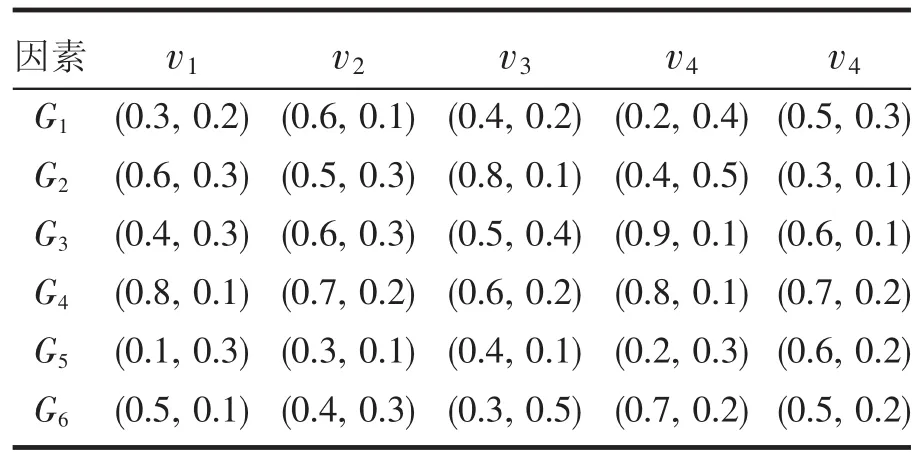
表1 手机的直觉模糊属性特征值

用文献[16]中给出的计算相似度的公式，

和文献[17]中给出的计算相异度的公式，

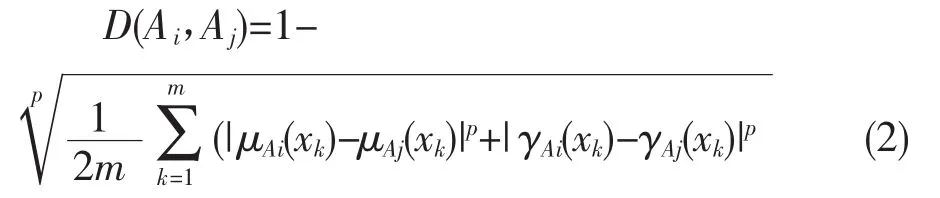
分别计算相似度和相异度作为手机Ai与Aj间的相关度(μij，γij)。为计算方便取p=1，用式(1)和式(2)求得手机间的直觉模糊相关矩阵为，

将手机之集做顶点集V={v1，v2，…，vn}，直觉模糊相似矩阵做边集，可得到半直觉模糊图。分别用基于求半直觉模糊图传递闭包图和最大生成树的两种聚类分析算法对进行分类。

如法炮制，取置信水平(0.45，0.45)会将手机分作2类{v1，v3，v4，v5}，{v2}；取置信水平(0.57，0)会将手机分作4类{v1，v5}，{v2}，{v3}，{v4}；取置信水平(p，q)＞(0.57，0)会将手机分作5类{v1}，{v2}，{v3}，{v4}，{v5}。再求的最大生成树得到，所示。当取置信水平，(0.45，0.47)会将手机分作1类{v1，v2，v3，v4，v5},如图2所示；取置信水平(0.45，0.45)会将手机分作2类{v1，v3，v4，v5}，{v2}如图2所示；取置信水平(0.47，0.44)会将手机分作3类{v1，v5}，{v3，v4}，{v2}。如图3所示；取置信水平(0.57，0.33)会将手机分作4类{v1，v5}，{v2}，{v3}，{v4}如图4所示；取置信水平(p，q)＞(0.57，0.33)会将手机分作5类，{v1}，{v2}，{v3}，{v4}，{v5}。

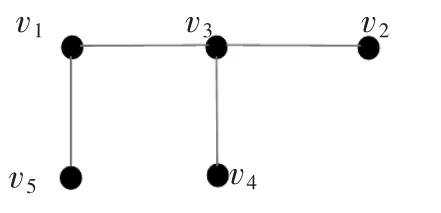
图1 最大生成树

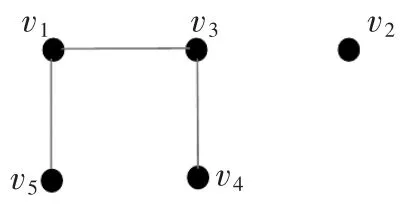
图2 置信水平(0.45，0.45)下分类结果

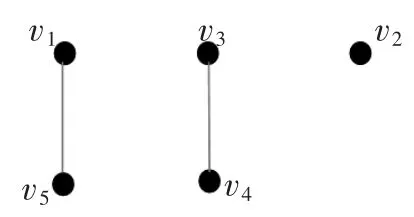
图3 置信水平(0.47，0.44)下分类结果

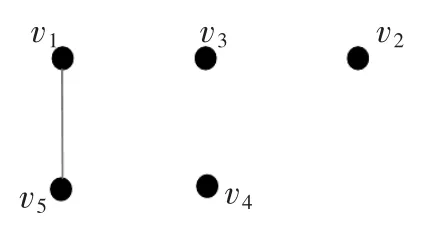
图4 置信水平(0.57，0.33)下分类结果

两种聚类分析算法分类结果一致；也与预设之手机类型结果一致。基于半直觉模糊图传递闭包和最大生成树的两种聚类分析算法都是合理有效的。

3 结语

讨论了半直觉模糊图的自反性、对称性和传递性。定义了半直觉模糊图的合成运算和幂运算。进而给出了半直觉模糊图传递闭包的定义。定义了半直觉模糊图相关边的序关系将经典图论中图的最小生成树的定义扩展到半直觉模糊图中给出了半直觉模糊图最大生成树的概念。提出了基于半直觉模糊图传递闭包和最大相关树的两种聚类分析算法。讨论了算法的合理性；分析了算法的复杂度。结合实例用这两种聚类分析算法做了基于半直觉模糊图聚类分析。结果显示此两种聚类分析算法聚类结果一致，并与预设分类结果一致，算法合理高效。

[1]ATANASSOV K．Intujtionistic Fuzzy sets[J].Fuzzy Sets And System,1986(1)：87-96．

[2]ZADEH L A.Fuzzy Sets[J].Information and Control,1965,8：338-353．

[3]CERRUTI U.Graphs and fuzzy graphs[C].New York：Fuzzy Inform ation and Decision Processes,1982：123-l31．

[4]TALAL AL H.Complete fuzzy graphs[J].International Journal of Mathematical Combinatonics,2011,4：26-34．

[5]MORDESON J N,NAIR P S.Cycles and cocycles of fuzzy graphs[J].Inform Sci,1996(90)：39-49．

[6]MORDESON J N，NAIR P S．Fuzzy graphs and fuzzy hypergraphs[M].New York：Physica Verlag,2000．

[7]E1GHOUL M.Folding of fuzzy graphs and fuzzy spheres[J].Fuzzy Sets and Systems,1993(58)：355-363．

[8]赵学靖,苏锦霞,杨凤翔.模糊图在生物群落聚类中的应用[J].兰州大学学报(自然科学版),2001,37(1)：14-18.

[9]廖丽平,胡仁杰.基于模糊图的模糊社会网络定义及其性质分析[J]．广西工业大学学报,2012,12(3)：14-18.

[10]杨文华,李生刚.区间值模糊图的运算性质[J].模糊系统与数学,2013,27(2)：127-135．

[11]鱼先锋.半直觉模糊图与应用[J].计算机工程与应用,2016,52(18)：88-91.

[12]张洪美,徐泽水,陈琦.直觉模糊集的聚类方法研究[J].控制与决策,2007,22(8)：882-888．

[13]贺正洪,雷英杰,王刚.基于直觉模糊聚类的目标识别[J].系统工程与电子技术,2011,33(6)：1283-1288.

[14]刘锁兰,王江涛,王建国,等.一种新的基于图论聚类的分割算[J].计算机科学,2008,25(9)：245-247.

[15]ZHAO F X，MA Z M，YAN L．Fuzzy clustering based on vague relations[C]∥Proc．of the Fuzzy Systems and Knowledge Discovery,2006：79-88．

[16]LIU W．New similarity measures between intuitionistic fuzzy sets and between elements[J].Mathematical and Computer Modelling,2005,42(1-2)：61-70．

[17]LID F．Some measures of dissimilarity in intuitionistic fuzzy structures[J].Journal of Computerand System Sciences,2004,68(1)：115-122．

（责任编辑：李堆淑）

Two Kinds of Clustering Analysis Algorithm Based on Half Intuitionistic Fuzzy Graph

YU Xian-feng,WAN Shi-chang
(School of Mathematics and Computer Application，Shangluo University，Shangluo 726000,Shaanxi)

The definition of transitive closure and maximum spanning tree of a half intuitionistic fuzzy graph is given.And then two kinds of clustering analysis algorithm are proposed based on transitive closure and maximum spanning tree of a half intuitionistic fuzzy graph.The rationality of the algorithms are discussed,and their complexity are analyzed.Combining with an example,we use the two clustering analysis algorithms for clustering analysis based on half intuitionistic fuzzy graph.The clustering analysis results show that the algorithm is reasonable and efficient.

half intuitionistic fuzzy graph;transitive closure;maximum spanning tree;clustering analysis

TP301.2

：A

：1674-0033（2017）04-0001-06

10.13440/j.slxy.1674-0033.2017.04.001

2017-05-12

陕西省教育厅专项科研计划项目（16JK1236）

鱼先锋，男，陕西商州人，硕士，讲师