基于Kramers-Kronig关系建立金属太赫兹色散模型∗
牟媛 吴振森†张耿 高艳卿 阳志强
1)(西安电子科技大学物理与光电工程学院,信息感知技术协同创新中心,西安 710071)
2)(中国科学院上海技术物理研究所,红外物理国家重点实验室,上海 200083)
3)(西安工业大学光电工程学院,西安 710021)
基于Kramers-Kronig关系建立金属太赫兹色散模型∗
牟媛1)吴振森1)†张耿1)高艳卿2)阳志强3)
1)(西安电子科技大学物理与光电工程学院,信息感知技术协同创新中心,西安 710071)
2)(中国科学院上海技术物理研究所,红外物理国家重点实验室,上海 200083)
3)(西安工业大学光电工程学院,西安 710021)
(2017年1月12日收到;2017年3月30日收到修改稿)
提出了一种基于测量反射率谱、使用Kramers-Kronig(KK)关系建立金属太赫兹色散模型的方法.结合合金铝和合金铜4—40 THz的测量反射率谱,通过反射系数振幅和相位的KK关系,采用高频端指数外推,低频端常数外推的方法,反演金属复折射率.以KK反演的复折射率作为实验值,以拟合复折射率和实验值误差最小为准则,使用遗传优化算法,拟合了合金铝和合金铜的Drude色散参数(等离子频率和碰撞频率).基于优化的Drude模型计算了0.1—40 THz材料的复折射率,与椭偏仪的实测结果符合,验证了模型的准确性.该方法理论与实验相互验证,以测量的复折射率作为实验定标,将远红外频段的色散信息拓展到太赫兹频域,确定了太赫兹频段金属的微观物理参数,提供了太赫兹频段色散和散射机理的研究依据.
太赫兹,远红外,Drude模型,Kramers-Kronig关系
1 引 言
材料的色散特性,如介电参数、磁导率、表面阻抗等是用来表征固体宏观光学性质的物理量,也是目标散射特性、通信及天线系统设计的重要基础[1,2].对于不同材料,如金属、绝缘体和半导体等,在不同频段内影响其介电性质的物理机制有所不同,但主要受三个物理过程约束:电子跃迁、晶格振动和自由载流子效应[3].常见的理论研究材料光学常数的模型为Lorentz电介质吸收模型和Drude金属吸收模型[4,5].在远红外频段,Drude模型适合于贵金属[6,7]、半导体[8,9]的介电参数研究,由于材料的微观色散参数如碰撞频率恰好位于太赫兹至远红外频段,因此太赫兹/远红外频段材料的色散特性引起了广泛的研究.Spitzer等[10,11]通过测量材料的透反射率谱,结合经典介电模型,研究了远红外频段石英晶体、铁电氧化材料BaTiO3,SrTiO3,TiO2等物质的色散关系.美国海军研究实验室在液氦环境中测量了InSb,InAs,GaSb,GaAs以及室温下InP和AlSb材料的反射率,使用Lorentz振子模型数值拟合了其反射率特性[12].Willis等[13,14]根据时域有限差分法,系统蒙特卡罗法和分子动力学法等算法,验证了Drude模型对于硅材料的适用性.Lucyszyn[15]证明了Drude经典模型可用来描述室温下常见金属的电损耗特性,为30 GHz—12 THz的计算机辅助设计测量仿真系统提供了材料色散特性的信息.但是,单一的Drude模型无法准确描述材料的带间传输特性,也无法在整个波谱内解释材料的色散特性,因而在太赫兹频段,需要采用不同的测量手段建立色散模型.Ordal等[16]根据非谐振腔实验测量了不同金属的吸收谱,结合吸收系数和折射率实部的Kramers-Kronig(KK)关系,反演了金属在亚毫米波频段的光学常数.Silfsten等[17]基于THz光谱仪测量了多孔材料的透射率谱,利用KK关系反演了0.5—2.0 THz的复折射率.目前,较为成熟的太赫兹时域光谱(THz-TDS)技术[18]和太赫兹椭偏技术[19]可以获得有限频点不同材料的光学参数.但是由于太赫兹辐射技术的局限,太赫兹实验系统需要提供真空或者低温的测量环境,实验样品需要保证严格的光学蚀刻标准,对表面粗糙度、样品厚度和材料掺杂度等加工工艺要求严苛,造成了太赫兹色散常数提取实验成本高、测量频点有限和稳定性差等缺点[20].由于材料的反射光谱包含丰富的物理信息,可用来定量研究材料的微观物理参数和光学常数,同时KK关系能更好地反映材料的带间跃迁效应,因而基于KK关系建立的经典介电模型将有利于太赫兹频段材料特性的研究及样品标准的确定.
文献[21]提出了基于不同合金的反射率谱,以远红外椭偏仪的测量复折射率作为实验定标,使用KK理论提取材料复折射率的方法.文献[21]以椭偏仪的测量复折射率为初值,对太赫兹频段的测量反射率谱进行了去噪平滑,获得了测量频段4—40 THz不同金属的复折射率.然而,由于定标复折射率位于远红外频段,因而在太赫兹低频端的复折射率反演将产生较大误差.同时,若材料反射率谱存在明显的带间跃迁效应,则无法依据单一频点的定标复折射率平滑宽频段的反射率谱.本文在文献[21]的基础上,以合金铝和合金铜的测量反射率谱与修正谱误差最小为原则[22],采用经典介电模型对测量反射率谱进行平滑滤波,可准确拟合测量反射率谱的频率特性,适用于金属、介质等多种材料.但是受太赫兹光谱测量中散射损耗及信噪比的影响,单纯通过反射率谱拟合的Drude介电模型无法准确描述材料在宽频带内的色散特性.因此,结合反射率振幅和相位的KK关系,依据滤波后的修正反射率谱,数值反演了与椭偏仪测量值相符合的金属复折射率.由于KK高频端外推指数因子适应于测量反射率谱,可减少反射率谱测量误差对反演复折射率的影响,有利于准确建立材料的色散模型.文中以KK反演的复折射率作为实验值,以拟合复折射率和实验值误差最小为目标函数,建立遗传优化模型,分别获得了0.1—20 THz及15—40 THz频域内金属的Drude色散模型,计算结果与椭偏仪测量的复折射率高度符合.该方法为太赫兹色散实验提供了理论校对,为研究材料太赫兹色散特性和散射机理提供了计算标准.
2 反射率谱的测量
在太赫兹至远红外频段,受趋肤效应的影响,入射波只能穿透纳米级厚度的金属薄膜,而对于常见的块状金属,透射能量几乎为0,反射率谱是分析其物理性质的有效实验手段之一.金属的反射率谱包含丰富的材料色散特性,反射率谱的定量分析可精确提取材料的复折射率和微观物理参数.当入射波垂直照射金属表面,反射率R与复折射率=n+iκ的关系为


其中,εr和εi分别为复介电参数的实部和虚部.复折射率的频率特性揭示了不同频段散射特性的微观机理,也决定了材料光谱特性的频率依赖性.在Drude近似模型中,复介电常数定义为


如图1所示,文献[21]采用Vertex 80V光谱仪,测量了合金铝和合金铜4—40 THz的反射率谱.然而,受光谱仪辐射和探测技术的影响,测量的反射率谱受系统噪声影响严重,尤其在太赫兹频段,反射率谱存在明显的噪声起伏.为了减少噪声对色散参数(如以及微观物理量(如ωp和γ0)的反演误差,需要对测量的反射率谱进行去噪平滑.

图1 合金铝和合金铜的测量反射率谱Fig.1.Measured re fl ection spectra of Al alloy and Cu alloy.
文献[21]使用远红外测量复折射率作为实验初值,对测量反射率谱进行平滑去噪,然而由于不同类型的材料具有不同的光谱频率分布特性,需要根据测量光谱的频率特性来选择合适的色散模型.文献[21]以单一频点的复折射率作为初值,无法拟合不同特性的反射率谱.实验证明,金属太赫兹/远红外反射率谱满足Drude经典介电模型[15].根据(4)式,Drude模型中的等离子频率ωp和碰撞频率γ0是确定介电模型的关键参数.由于ωp和γ0无法通过实验直接获得,因而采用材料测量反射率谱来进行优化反演计算.使用遗传算法,通过确定目标函数(6)式来反演未知参数的最优解[22]:
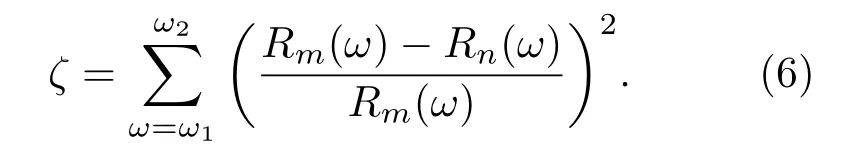
文献[16]中测量了金属Al在亚毫米波段的反射率谱,以4.0—40 THz频段为例 (如图2所示),结合遗传算法,反演最优的ωp和γ0,设定遗传参数,采用二进制的编码方法,变量的2进制位数为20,最大迭代代数为1200代,初始种群数目为80,选择概率为0.9,重组概率为0.7,目标函数(6)式于500代收敛于0,等离子频率的收敛结果为ωp=6194.49 THz,碰撞频率为γ0=41.76 THz,如图2所示.
根据图2反演的最优ωp和γ0,代入(5)式中,获得Al的Drude反射率拟合谱.如图3所示,反射率拟合谱与测量谱符合.采用同样的方法,对傅里叶光谱仪测量的反射率谱进行平滑滤波.图4(a)和图4(b)为利用远红外源测量的4—20 THz铝和铜的反射率谱,图4(c)和图4(d)为利用中红外源测量的15—40 THz的反射率谱.由于中红外源信噪比较高,因而测量的反射光谱相对平滑.采用(6)式对图4中反射率测量谱进行平滑,反演的最优ωp和γ0如表1所列.

图2 反演的碰撞频率和等离子频率Fig.2.Inversed damping frequency and plasma frequency.

图3 文献[16]中Al的反射率测量谱及Drude修正谱Fig.3.Re fl ection spectra from Ref.[16]and its smoothed Drude spetra.

表1 使用遗传算法拟合合金铝和合金铜的等离子频率和碰撞频率Table 1.Optimized plasma frequency and damping frequency of Al alloy and Cu alloy using genetic algorithm.

图4 合金铝和合金铜的测量反射率谱及修正谱 (a)合金铝4—20 THz;(b)合金铜4—20 THz;(c)合金铝15—40 THz;(d)合金铜15—40 THzFig.4.Measured and smoothed re fl ection spectra of Al alloy and Cu alloy:(a)Al alloy from 4–20 THz;(b)Cu alloy from 4–20 THz;(c)Al alloy from 15–40 THz;(d)Cu alloy from 15–40 THz.
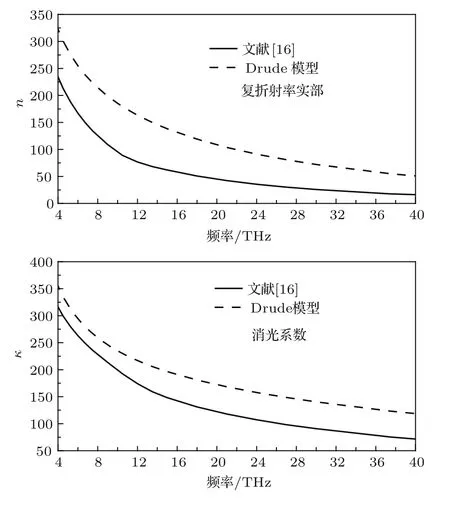
图5 文献[16]中Al拟合复折射率与实测结果的对比Fig.5.Comparison of the measured and fi tted complex refractivity of Al in Ref.[16].
将表1计算的Drude参数代入到(5)和(1)式,获得优化后的反射率谱.如图4所示,优化后的Drude反射率谱消除了测量反射率谱的噪声起伏,谱线的变化趋势与测量谱符合,为提取材料的介电参数提供了数据基础.
但是基于反射率谱反演的ωp和γ0在宽频谱范围内无法精确拟合材料的复折射率.将图2中拟合的等离子频率和碰撞频率代入(5)式中,获得文献[16]中金属Al的拟合复折射率,如图5所示,实折射率n和消光系数κ的测量值(如实线所示)与拟合值(如虚线所示)具有相同的谱线趋势,但是单位频点上的拟合值与真实值之间存在一定的误差.因此根据(6)式优化获得的Drude模型虽然可以拟合金属的反射率谱特性,却无法在较宽频带内拟合材料的复折射率.因而需要引入KK关系对测量的反射率谱进行复折射率的提取.
3 利用KK关系建立Drude色散模型
KK关系具有严格的因果性、线性和解析性,因而相比于其他测量手段,KK关系只依赖于材料的透/反射率谱,对实验设备的要求低,测量频谱宽,测量过程简单.已知材料的反射率谱R(ω),通过KK积分关系(7)式得到反射系数的相位谱信息[23]:

其中,ω为圆频率,P为柯西积分主值,R表示反射率.反射率R与反射系数r满足如下关系:

其中,r∗表示反射系数的共轭,r0为反射系数振幅,θ为反射系数相位.当ω′位于测量区间(ωa,ωb),即ωa< ω′< ωb时,R为测量值,当0< ω′< ωa时,采用常数外推,令R(ω′)=R(ωa);当ωb< ω′< ∞时,采用指数外推,令R(ω′)=R(ωb)(ω′/ωb)−p,p为外推指数因子.由(9)式求得材料的折射率和消光系数:

指数因子p一般取决于复折射率的定标值.通常定标复折射率为单位频点或者有限区间的测量复折射率,可由THz-TDS系统、椭偏仪等实验系统测量获得.以图3中修正后的反射率谱为例,当p=0.035时,反演的复折射率与测量值高度符合(图6),验证了基于修正反射率谱反演材料复折射率的准确性.其中反演误差主要来源于反射率修正谱与测量谱的误差以及KK法自身积分所产生的误差.
本文以文献[21]中的测量复折射率作为定标值,基于反射率修正谱(如图4所示),反演合金铝和合金铜的复折射率.然而由于太赫兹辐射源信噪比的局限性,测量的反射率谱存在微小的能量损耗,从而影响了基于KK法提取材料光学常数的精确性.对比图4(a)和图4(c)以及图4(b)和图4(d)中15—20 THz的反射率,对4—20 THz的修正反射率谱进行能量补偿,确保同一材料相同频段内的反射率基本符合.基于修正后的反射率谱,图7和图8使用KK法反演合金铝和合金铜的4—40 THz的复折射率.图7(a)中,p=2.5,图7(b)中,p=0.22,合金铝的反演复折射率与相同区间内椭偏仪测量值符合.图8(a)中,p=3.2,图8(b)中,p=0.4.指数参数p的差异来源于反演区间的不同以及反射率修正谱的误差.因而,调整指数因子p可减小反射率谱的测量误差对复折射率提取所造成的影响.

图6 基于文献[16]Drude修正谱的KK反演复折射率Fig.6. Inversed complex refractivity based on the Drude smoothed re fl ection spectra in Ref.[16].

图7 基于反射率修正谱反演合金铝的复折射率 (a)4—20 THz;(b)15—40 THzFig.7.Inversion of complex refractivity based on the fi tted re fl ection spectra of Al alloy:(a)4–20 THz;(b)15–40 THz.

图8 基于反射率修正谱反演合金铜的复折射率 (a)4—20 THz;(b)15—40 THzFig.8.Inversion of complex refractivity based on the fi tted re fl ection spectra of Cu alloy:(a)4–20 THz;(b)15–40 THz.
分析(5)式可知,通过KK关系从反射率谱中提取的复折射率,可以定量分析材料的微观物理参数.根据(5)式,Drude模型的参数γ0和ωp可通过下式获得:

通过已知的复折射率(复介电参数),基于遗传算法,建立目标函数ζ:

其中,εr,ie代表已知的复介电参数,εr,i为拟合的复介电参数.采用遗传算法寻找最优解,当目标函数(11)惟一收敛到最小值,相应的Drude参数(ωp,γ0)即为最优拟合值.
由文献[24]可知,采用(11)式获得的拟合Drude参数(ωp,γ0)随着拟合频点的不同而不同.为了减少复介电参数测量/反演的误差对Drude参数的影响,需要对N 个拟合频点的最优(ωpi,γ0i)求平均:

文献[16]和文献[6]中分别列举了金属铝和铜的远红外复折射率.其中,铝的Durde拟合参数分别为γ0=12.72 THz,ωp=2862 THz;铜的拟合参数为γ0=2.196 THz,ωp=1788 THz.图9分别拟合了铝1.5—12 THz以及铜5.4—12 THz的复折射率,拟合Drude参数分别为γ0=13.07 THz,ωp=2885.1 THz和γ0=2.54 THz,ωp=1762.1 THz,与文献[16]和文献[6]的Drude拟合参数基本一致.由(5)式可知,由于拟合的ωp≫γ0,因而Drude拟合参数的误差对消光系数κ影响较小;同时,铜的平均碰撞频率γ0与拟合频率ω的值相当,因而铜的实折射率拟合值相较于铝的实折射率拟合存在相对明显的误差.
结合椭偏仪测量的合金铝和合金铜的复折射率,分别以18.6,20.5,28.0,32.4 THz作为拟合频点,获得相应的Drude参数拟合结果,如表2所列.由于(ωp,γ0)的最优解随着拟合频点的不同而变化,因而,对优化的参数分别求平均值.其中,合金铝的平均等离子体频率ωp=4066.3 THz,平均碰撞频率γ0=7.87 THz,合金铜的平均等离子体频率ωp=3141.0 THz,平均碰撞频率γ0=7.60 THz.

表2 基于椭偏仪测量合金复折射率的Drude模型参数拟合Table 2.The optimized Drude parameters of metals based on the measured complex refractivity by ellipsometer.
相应地,基于15—40 THz的反演复折射率(如图7(b)和图8(b)所示),结合(11)式,分别拟合在18.6,20.5,28.0,32.4 THz下的Drude模型参数,合金铝的平均等离子频率为3749.0 THz,与椭偏仪的拟合误差为7.8%;碰撞频率为8.93 THz,与椭偏仪的拟合误差为13.5%;合金铜的平均等离子频率为3254.0 THz,误差为3.6%,平均碰撞频率为8.14 THz,误差为7.0%,如表3所列.其中误差主要来源是椭偏仪自身复折射率的测量误差以及KK反演复折射率的误差等.
分别将表2和表3中的Drude模型参数代入(5)式中,计算15—40 THz下合金铝和合金铜的复折射率,如图10所示.其中,空心圆线表示基于椭偏仪测量值拟合的Drude模型,实心圆线表示基于KK反演的复折射率拟合的Drude模型.如图10所示,两者所获得的复折射率与椭偏仪的测量值符合,且根据KK关系建立的Drude介电模型的拟合结果与椭偏仪实测值之间误差优于20%,论证了基于KK反演建立的Drude色散模型在宽频带内分析材料复折射率的准确性.

图9 基于铝和铜的文献复折射率建立Drude模型 (a)铝;(b)铜Fig.9.The Drude models optimized from the complex refractivity of References:(a)Al;(b)Cu.

表3 基于15—40 THz的反演复折射率拟合的Drude模型参数Table 3.The optimized Drude parameters based on KK inversed complex refractivity from 15–40 THz.

图10 Drude拟合的复折射率与椭偏仪测量结果的比较(15—40 THz) (a)合金铝;(b)合金铜Fig.10.Comparison of complex refractivity from Drude fi tness and ellipsometer measurement(15–40 THz):(a)Al alloy;(b)Cu alloy.
表4列出了基于4—20 THz KK反演的复折射率(如图7(a)和图8(a)所示)在各个拟合频点上的Drude模型参数的平均值(简称数值结果).合金铝等离子频率的数值结果为3435.6 THz,碰撞频率的数值结果为8.0 THz.图11基于表4的Drude参数拟合了合金铝和合金铜在0.1—20 THz的复折射率,与KK反演的复折射率和椭偏仪测量的复折射率相符合.

表4 基于4—20 THz反演复折射率的Drude模型参数拟合Table 4.The optimized Drude parameters based on KK inversed complex refractivity in the region of 4–20 THz.

图11 Drude拟合的复折射率与椭偏仪测量结果的比较(0.1—20 THz) (a)合金铝;(b)合金铜Fig.11.Comparison of complex refractivity from Drude fi tness and ellipsometer measurement(0.1–20 THz):(a)Al alloy;(b)Cu alloy.
如图10和图11所示,依据KK关系反演的复折射率可以建立金属的Drude模型,拟合结果与椭偏仪实测值符合.该方法的准确性取决于反射率光谱与椭偏仪定标复折射率的测量精度,反射率谱越接近于真实值,定标复折射率精度越高,则KK反演的复折射率越精确,建立的色散模型也更加准确.因而,该方法也对太赫兹频段反射率谱的测量以及单频点复折射率测量实验的精度提出了更高的要求.
4 结 论
本文提出一种联合傅里叶光谱仪和远红外椭偏仪建立金属太赫兹色散模型的方法.利用远红外椭偏仪测量的复折射率值为定标,结合傅里叶光谱仪测量的太赫兹/远红外反射率谱,采用反射系数幅度和相位的KK关系,调整指数外推参数,直至反演结果与椭偏仪定标复折射率符合为止.基于遗传算法,建立与椭偏仪实测复折射率和KK反演复折射率符合良好的Drude经典色散模型.为了减少反射率测量谱的噪声对KK反演的影响,以Drude色散模型为基础,以修正反射率谱与测量谱误差最小为原则,对反射率测量谱进行平滑去噪.去噪后的反射率谱与测量谱符合,消除了噪声起伏对KK反演的影响.KK关系采用了高频端指数外推、低频端常数外推的方法,其中KK指数因子的调整可以弥补反射率谱测量产生的能量损耗,提高了KK反演的可靠性.由于在4 THz以下,反射率谱测量误差较大,且椭偏仪所获得的定标复折射率位于远红外频段,因而KK法只反演了4—40 THz的复折射率.文中结合KK反演的复折射率,拟合了0.1—20 THz频段的Drude模型,获得了太赫兹低频端的色散参数,为太赫兹色散实验和散射分析提供了理论依据.该方法以有限频段内的实验值为基础,获得了更宽频段的复折射率,实现了宽频带复折射率的测量提取.基于KK关系建立经典色散模型的关键在于精确的反射率谱和定标复折射率的测量(其中定标复折射率可以由THz-TDS系统或太赫兹椭偏技术等获得),测量精度越高,KK反演越精确,拟合的色散模型也更精确.该方法利用了现阶段THz频段复折射率测量频点有限的特点,将有限频段色散特性的研究拓展到更宽频段.由于KK关系可以更好地反映材料的带间跃迁效应,因而该方法可通过选择不同的色散模型,适应不同材料(如半导体、介质等)的色散模型拟合,为太赫兹材料散射特性和太赫兹雷达成像技术的发展提供了研究基础.
[1]Li Z,Cui T J,Zhong X J,Tao Y B,Lin H 2009 IEEE Antenn.Propag.Mag.51 39
[2]Piesiewicz R,Jansen C,Mittleman D,Kleine-Ostmann T,Koch M,Kürner T 2007 IEEE Trans.Antenn.Propag.55 3002
[3]Chen Q 2012 M.S.Thesis(Harbin:Harbin Institute of Technology)(in Chinese)[陈琦2012硕士学位论文 (哈尔滨:哈尔滨工业大学)]
[4]Wang L,Zhou Q 2007 Coll.Phys.26 48(in Chinese)[王磊,周庆2007大学物理 26 48]
[5]Su J,Sun C,Wang X Q 2013 Optron.Lasers 24 408(in Chinese)[苏杰,孙诚,王晓秋 2013光电子·激光 24 408]
[6]Ordal M A,Bell R J,Alexander Jr R W,Long L L,Querry M R 1985 Appl.Opt.24 4493
[7]Ordal M A,Long L L,Bell R J,Bell S E,Bell R R,Alexander Jr R W,Ward C A 1983 Appl.Opt.22 1099
[8]Loewenstein E V,Smith D R,Morgan R L 1973 Appl.Opt.12 398
[9]Ohba T,Ikawa S I 1988 J.Appl.Phys.64 4141
[10]Spitzer W G,Miller R C,Kleinman D A,Howarth L E 1962 Phys.Rev.126 1710
[11]Spitzer W G,Kleinman D A 1961 Phys.Rev.121 1324
[12]Hass M,Henvis B W 1962 J.Phys.Chem.Solids 23 1099
[13]Wills K,Knezevic I,Hagness S C 2013 Radio Science Meeting(Joint with AP-S Symposium)USNC-URSI Orlando,USA,July 7–13,2013 p154
[14]Willis K J,Hagness S C,Knezevic I 2011 J.Appl.Phys.110 063714
[15]Lucyszyn S 2004 IEEE Proc.-Microw.Antenn.Propag.151 321
[16]Ordal M A,Bell R J,Alexander Jr R W,Newquist L A,Querry M R 1988 Appl.Opt.27 1203
[17]Silfsten P,Kontturi V,Ervasti T,Ketolainen J,Peiponen K E 2011 Opt.Lett.36 778
[18]Duvillaret L,Garet F,Coutaz J L 1996 IEEE J.Sel.Top.Quantum Electron 2 739
[19]Yamashita T,Suga M,Okada T,Irisawa A,Imamura M 2015 40th International Conference on Infrared,Millimeter,and Terahertz Waves(IRMMW-THz)Hong Kong,China,August 23–28,2015 p1
[20]Kirley M P,Booske J H 2015 IEEE Trans.THz Sci.Technol.5 1012
[21]Mou Y,Wu Z S,Gao Y Q,Yang Z Q,Yang Q J 2017 Infrared Phys.Technol.80 58
[22]Cheng X H,Tang L G,Chen Z T,Gong M,Yu T J,Zhang G Y,Shi R Y 2008 Acta Phys.Sin.57 5875(in Chinese)[程兴华,唐龙谷,陈志涛,龚敏,于彤军,张国义,石瑞英2008物理学报57 5875]
[23]Lucarini V,Peiponen K E,Saarinen J J,Vartiainen E M 2005 Kramers-Kronig Relations in Optical Materials Research(New York:Springer Berlin Heidelberg)pp27–50
[24]Wang R J,Deng B,Wang H Q,Qin Y L 2014 Acta Phys.Sin.63 134102(in Chinese)[王瑞君,邓斌,王宏强,秦玉亮2014物理学报63 134102]
PACS:02.30.Zz,07.60.–j,78.20.–e,78.20.CiDOI:10.7498/aps.66.120202
Establishment of THz dispersion model of metals based on Kramers-Kronig relation∗
Mou Yuan1)Wu Zhen-Sen1)†Zhang Geng1)Gao Yan-Qing2)Yang Zhi-Qiang3)
1)(Collaboration Innovation Center of Information Sensing and Understanding,School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China)
2)(National Laboratory of Infrared Physics,Shanghai Institute of Technical Physics,Chinese Academy of Sciences,Shanghai 200083,China)
3)(School of Optoelectronic Engineering,Xi’an Technological University,Xi’an 710021,China)
12 January 2017;revised manuscript
30 March 2017)
The extraction of terahertz dispersion parameters is con fi ned in a limited region due to the limitation of the existing THz techniques.A method of studying the dispersion model of metals from the measurements of re fl ection spectrum and analysis of Kramers-Kronig(KK)relation is proposed.The re fl ection spectrum is measured by Vertex 80V Fourier transform spectrometer.In order to eliminate the signal noise of measured re fl ection spectrum,the measured spectrum is smoothed by Drude estimation.Using the smoothed re fl ection spectra of copper(Cu)alloy and aluminum(Al)alloy in a range of 4–40 THz,the complex refractivities are inversed based on the KK relation of amplitude and phase of re fl ective coefficient.The constant extrapolations at lower frequencies and the exponential extrapolation at higher frequencies are adopted in the KK integration.The exponential extrapolation index is adjusted according to the calibrating complex refractivity measured from far-infrared ellipsometer.According to the inversed complex refractivity,the plasma frequency and damping frequency in Drude model are optimized using the genetic algorithm.The objective function is de fi ned as the error between the fi tted complex refractivity and KK inversion.Since the optimal plasma frequency and damping frequency are di ff erent for di ff erent fi tting frequencies,the obtained Drude parameters are averaged in order to reduce the in fl uences of errors from KK inversion,measured re fl ection spectrum and calibrations.The complex refractivity indexes in a range from 15 THz to 40 THz,calculated by the established Drude model,are in good agreement with the measured calibrations from ellipsometer,which demonstrates the accuracy of the established Drude dispersion model.The re fl ection spectra below 4 THz are greatly distorted due to the signal noise,and the calibrating refractivity is located in the far infrared region,thus the complex refractivity is inversed in a region of 4–40 THz by KK algorithm.The complex refractivity indexes in a range of 0.1–20 THz,obtained by the proposed scheme,are for the vacancy,which will provide great support for the dispersion analysis in the whole terahertz gap.The procedures are helpful for extrapolating the dispersion information to terahertz band from the far infrared region.The scheme takes the advantage of the spectrometer and ellipsometer,and it requires high experimental precisions of re fl ection spectrum and calibrating refractivity.In addition,the scheme is adaptive to both metals and nonmetals by applying proper dispersion model which depends on the property of the re fl ection spectrum.The established model determines the microscopic dispersion parameters of material,which provides great support for the investigation of terahertz dispersion analysis,scattering mechanisms and imaging processes.
terahertz,far infrared,Drude model,Kramers-Kronig relation
10.7498/aps.66.120202
∗国家自然科学基金(批准号:61571355)资助的课题.
†通信作者.E-mail:wuzhs@mail.xidian.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Natural Science Foundation of China(Grant No.61571355).
†Corresponding author.E-mail:wuzhs@mail.xidian.edu.cn

