缀饰格子中时间反演对称破缺的量子自旋霍尔效应∗
耿虎 计青山 张存喜 王瑞†
1)(浙江海洋大学电子信息科学与工程系,舟山 316022)
2)(浙江海洋大学东海科学与技术学院,舟山 316000)
缀饰格子中时间反演对称破缺的量子自旋霍尔效应∗
耿虎1)计青山2)张存喜1)王瑞1)†
1)(浙江海洋大学电子信息科学与工程系,舟山 316022)
2)(浙江海洋大学东海科学与技术学院,舟山 316000)
(2016年12月8日收到;2017年4月17日收到修改稿)
研究了缀饰格子中的量子自旋霍尔效应,模型中同时考虑了Rashba自旋轨道耦合和交换场的作用.缀饰格子具有简立方对称性,以零能平带和单狄拉克锥结构为主要特点.在缀饰格子中,不论是实现量子自旋霍尔效应还是量子反常霍尔效应,都需要一个不为零的内禀自旋轨道耦合作用来打开一个完全的体能隙,这与石墨烯等六角格子模型有着很大的不同.在交换场破坏了时间反演对称性的情况下,以自旋陈数为标志的量子自旋霍尔效应仍然能够存在,边缘态和极化率的相关结果也证明了这一结论.结果表明自旋陈数比z2拓扑数在表征量子自旋霍尔效应方面有着更广泛的适用范围,相应的结论为利用磁场控制量子自旋霍尔效应提出了一个理论模型和依据.
量子自旋霍尔效应,自旋轨道耦合,拓扑序
1 引 言
近年来,量子自旋霍尔效应和量子反常霍尔效应[1−5]由于其在基础物理和纳米电子学等方面潜在的应用而得到了广泛的关注和研究[6−9].量子自旋霍尔效应和量子反常霍尔效应都以完全打开的体能隙和受到拓扑保护的无能隙边缘态著称,可以用一些拓扑不变量来表征[10].最初,Kane和Mele[11]预言绝缘体在没有外磁场的情况下,可以发生量子自旋霍尔效应,块体表面会出现受时间反演对称保护的螺旋边缘态,这一现象已经在碲化汞量子阱中得到了很好的验证[12,13].后来,南京大学盛利研究组[14,15]发现,当内禀自旋轨道耦合和Rashba自旋轨道耦合同时存在时,在时间反演对称破缺的情况下量子自旋霍尔效应仍然能够存在.这一发现大大拓展了量子自旋霍尔效应的范围并提出了一个新的拓扑不变量——自旋陈数[14−16].
一般情况下,内禀自旋轨道耦合作用被认为有助于实现量子自旋霍尔效应,而Rashba自旋轨道耦合则不利于这一效应,它有助于实现量子反常霍尔效应[17].量子反常霍尔效应依赖于系统的内在磁化和Rashba自旋轨道耦合,它可以被一个整数化的霍尔电导来表征[18−22].目前,人们已经在数个模型中实现了量子反常霍尔效应.Wu[23]建议在石墨烯中通过对自旋轨道作用强度的调节来改变能带的拓扑性,从而实现量子反常霍尔效应.同样是在石墨烯中,中国科学技术大学的乔振华教授等[17]认为Rashba自旋轨道耦合和外磁场的共同作用可以打开狄拉克点的能隙,从而产生量子反常霍尔效应.近来,人们陆续在许多其他的模型(如Kagome模型[24−26]、四方氧化晶格[27]、星形晶格[28]等)中研究了量子反常霍尔效应和拓扑量子相变.
本文研究了时间反演对称破缺情况下缀饰格子中的量子自旋霍尔效应[29−32].缀饰格子也称为二维正方边心格子或者Lieb格子,把两个正方格子相互嵌套即可形成一个缀饰格子,其全称为具有各向同性最近邻跃迁的正方边心格子[33,34].与Kagome格子、石墨烯等已经得到很多研究的模型不同,二维正方边心格子具有简立方对称结构,从而展示出一些独有的特性.
首先,正方边心格子和Kagome格子的原胞中均包含有三个不同的原子,对应着两个色散带和一个平带,但Kagome格子中的平带为其最高能带,而正方边心格子能谱中的平带则位于两支色散带的中间且能量为零,我们称其为零能平带,这也是正方边心格子最为显著的特点.其次,正方边心格子的第一布里渊区中只包含有一个狄拉克锥结构,体能带中的较高色散带和较低色散带在M点接触到中间的零能平带从而形成狄拉克锥,而石墨烯和Kagome格子模型则是双狄拉克锥结构.值得指出的是,在没有内禀自旋轨道耦合的情况下,正方边心格子能谱在M点的能隙将始终保持关闭.在这一模型中,不论是实现量子自旋霍尔效应还是量子反常霍尔效应,要想在体能带打开一个完整的能隙,一个非零的内禀自旋轨道耦合是必要条件之一.
2 正方边心格子的能带
正方边心格子的几何结构如图1(a)所示,格子中每个原胞均包含三个不同的原子,分别标记为A,B,C,最近邻格点之间的距离为a,在后面的计算中我们把a作为长度的基本单元.图1(b)给出了这类格子的第一布里渊区并标记出了所有的高对称点Y,Γ,M和X,其中的红色虚线Γ-M-X-Γ给出了色散关系的积分路径.
在紧束缚近似下,正方边心格子的哈密顿量可以写为HNN,HSO,HR以及Hg四个部分的组合.这里,HNN是强度为t的最近邻格点之间的跃迁:
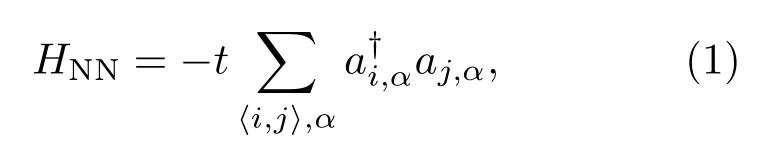
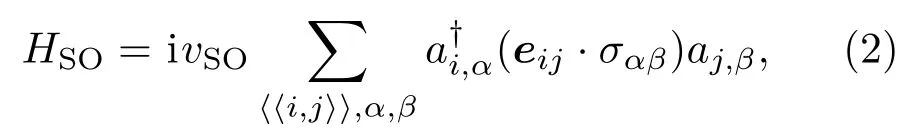
这里vSO是内禀自旋轨道耦合的强度,β同样为自旋指标,σ是泡利矩阵,i和j是两个次近邻格点的坐标,k是它们的公共最近邻.单位矢量eij的形式为的方向为从k点指向i点.
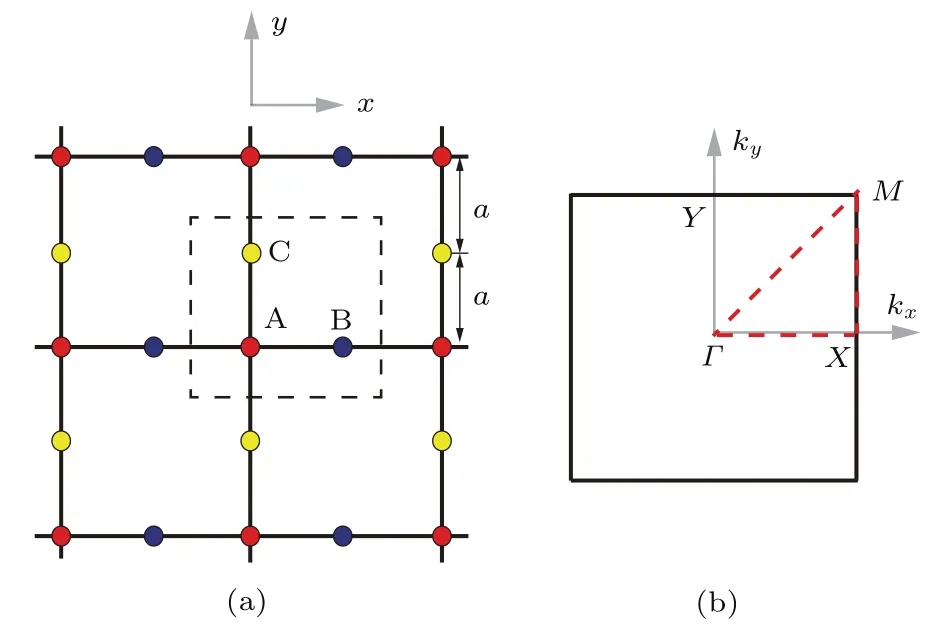
图1 (网刊彩色)正方边心格子 (a)几何结构;(b)第一布里渊区Fig.1.(color online)(a)The geometry and(b)the fi rst Brillouin zone of Lieb lattice.
HR代表作用在最近邻格点之间的强度为vR的Rashba自旋轨道耦合:
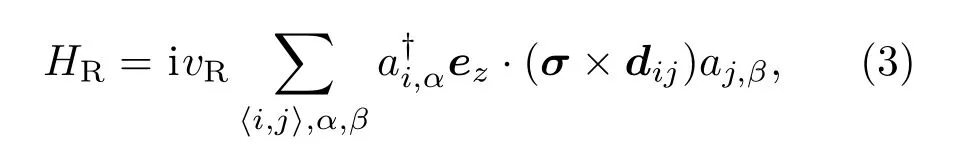
其中,ez为z方向的单位矢量.第四部分Hg表示强度为g的交换场作用,把一个磁绝缘体压附在二维材料上,其可与薄膜中的载流子进行耦合从而形成交换场,
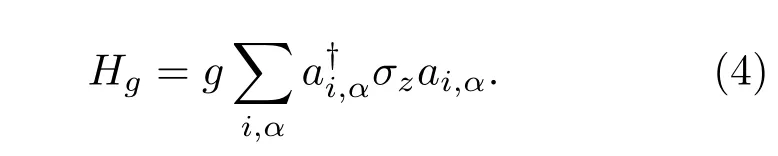
本文中,我们把最近邻格点之间的跃迁强度t作为能量的基本单元,其他量纲为能量的参数如内禀自旋轨道耦合强度、Rashba自旋轨道耦合强度、交换场的大小以及费米能级等均以t作为基础.在动量空间中,选择恰当的基矢Ψ(k)=[Ci,k,↑,Ci,k,↓]T(i=A,B,C), 可以把哈密顿量展开为一个矩阵U(k).数值对角化此矩阵,就可以得到正方边心格子的体能带.
正方边心格子以零能平带著称,当取g=0,vR=0和vSO=0时,即可看到其处于简并状态的能带,两个色散带在M点与中间的零能平带相接触,从而形成狄拉克锥结构,如图2(a).值得指出的是,能带在M点的简并即使在交换场和Rashba自旋轨道耦合不为零的情况下也有可能存在.事实上把M点的坐标代入哈密顿矩阵U(k),即可得到该点的6个能量本征值为当vSO=0时,在处将形成能级的简并,这一简并与交换场的强度无关.
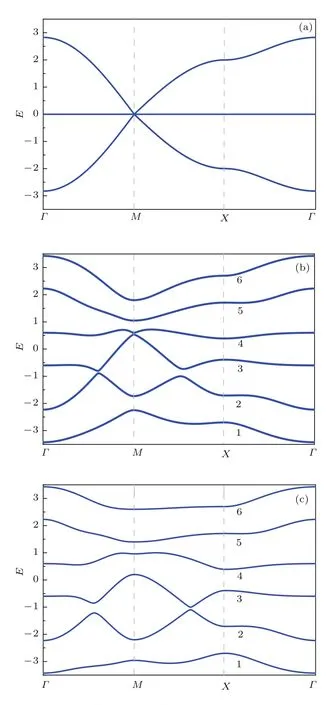
图2 (网刊彩色)正方边心格子的能带结构 (a)vR=0,g=0,vSO=0;(b)vR=0.4,g=0.6,vSO=0.3;(c)vR=0.4,g=0.6,vSO=0.5Fig.2.(color online)The evolution of band structures of Lieb lattice:(a)Pristine Lieb lattice;(b)vR=0.4,g=0.6 and vSO=0.3;(c)vR=0.4,g=0.6 and vSO=0.5.
所以,为了使能级在M点分开,内禀的自旋轨道耦合就一定不能为零.图2(b)和图2(c)中,我们给出了在不同内禀自旋轨道耦合强度的情况下系统的能谱,可以看出系统的6个能级在第一布里渊区中每一点都被很好地分开.量子自旋霍尔效应要求在能带结构中必须有一个完全打开的能隙,这要求较低能级的最大值要小于上方相邻能级的最小值,可以在这两个能级之间画出一条不与两个能级相交的直线.图2(b)中我们取参数vSO=0.3,g=0.6,vR=0.4,此时,系统在1/3和2/3填充模式下,均可以处于绝缘相,但当系统处于1/2填充时,我们无法在第3和第4能级之间画出一条不与这两个能级相交的直线,这意味着一个1/2填充系统的第三和第四能级总是被电子部分占据,我们把这种情况下的块体称为半金属,其霍尔电导不是一个整数[35].图2(c)中,我们在保持交换场和Rashba自旋轨道耦合强度不变的情况下,增大内禀自旋轨道耦合强度vSO=0.5,可以看出,系统存在非常明显的能隙,在1/3,1/2以及2/3等填充模式下均可以处于绝缘相.
一般地,可以用一个拓扑不变量来标识量子自旋霍尔效应.对本文所采用的量而言,外加交换场破坏了时间反演对称性,这使得z2指标不能用来衡量系统的拓扑性,但是另一个非常重要的拓扑不变量——自旋陈数依旧适用[14−16].我们以一个1/3填充的系统为例来说明自旋陈数的定义和计算.矩阵U(k)的6个本征函数中,可以根据电子的具体填充情况分为导带波函数和价带波函数,在1/3填充的情况下,可以把价带波函数φ1和φ2组成一个基矢,然后把算符σz⊗I3×3在这一基矢中展开成一个2×2的矩阵:
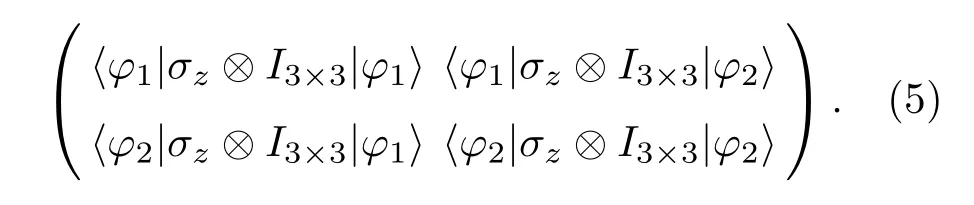
对角化(5)式所示矩阵,可以得到两个本征波函数ϕ±,然后算符σz的本征谱可以写为ψ±=[φ1,φ2]ϕ±.定义F±(k)=iez·[∇k×〈ψ±|∇k|ψ±⟩]即可得到每个自旋矢量(组分)的陈数:
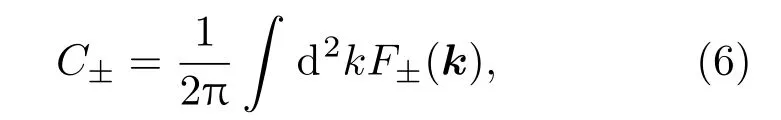
两个自旋矢量陈数的差即为自旋陈数,
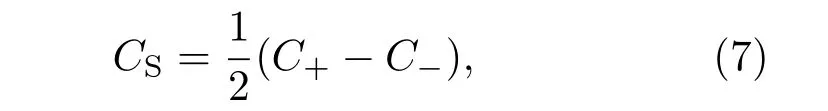
一个非零的自旋陈数CS标志着系统处于量子自旋霍尔相.但当自旋陈数为零时,系统可能处于量子反常霍尔态和普通绝缘相,可以借助于第一陈数这一拓扑序来区分这两个态,把两个自旋矢量的陈数简单求和就可以得到第一陈数(TKNN数):

这样,结合第一陈数和自旋陈数,我们就可以很容易地区分出量子自旋霍尔态、量子反常霍尔态和普通绝缘体.当C=0,CS̸=0时,系统处于量子自旋霍尔态;当C=0,CS=0时,系统为普通的绝缘体;当C̸=0,CS=0时,系统处于量子反常霍尔态.
量子自旋霍尔效应特点也反映在其螺旋性的边缘态分布.图3(a)给出了含有边缘态的正方边心格子的能谱(为了更清楚地显示边缘态的存在,这里只截取了部分能谱),系统在x方向具有完整的周期性而在y方向具有开放的边界,系统的参数设置和图2(b)一致,vR=0.4,g=0.6,vSO=0.3.必须指出的是,Kane和Mele[11]最早提出的量子自旋霍尔效应由于受到时间反演对称的保护,其边缘态是真正的(没有间隙)相交,这一状态可以被z2拓扑序所表征.但是在我们的模型中,交换场的引入破坏了系统的时间反演对称性,这将导致开边界系统能谱中的能级会在相交点打开一个非常小的能隙,而不再如同时间反演对称保护下无能隙的相交.可以看出,这类状态与真正的量子自旋霍尔态还是有所区别的,它是一种时间反演对称破缺的量子自旋霍尔效应[14],不能为z2拓扑序所表征,而是被一个全新的拓扑不变量——自旋陈数CS所表征.当费米能级选择为EF=−1.00时,存在四个不同的边缘态,根据速度公式可以知道边缘态A和D沿+x方向传播,而B和C态则沿着−x方向传播.
图3(b)给出了图3(a)中四个边缘态的波函数分布,图中的横坐标为系统在y方向的原胞排列,本文中,我们考虑系统在y方向有120个原胞.每个原胞上的|ψ|2均包含了A,B和C三个原子的贡献.总体而言,|ψ|2主要分布在系统边界约三个原胞的宽度范围内,其中B态和D态局域在系统的同一个边界,而A态和C态则局域在系统的另一个边界.结合速度的情况得出,分布在系统同一个边界的两个态沿着相反的方向传播,因而不存在电流.

图3 (网刊彩色)1/3填充下的正方边心格子 (a)带有费米能级的能谱(部分);(b)边缘态波函数分布Fig.3.(color online)(a)Energy spectrum of Lieb lattice ribbons for a 1/3 fi led system(the Fermi level corresponds to four edge states);(b)wave-function distributions across the width for the edge states.
判断体系是否存在量子自旋霍尔效应还有一个重要的参照就是边缘态的自旋极化率.可以用两个自旋组分的差除以它们的和来表示自旋极化率,有在我们的模型中,Rashba自旋轨道耦合把自旋向上组分和向下组分混合在一起,电子很难达到完全的极化,转而只能在合适的参数设置下,尽可能地获得某种组分比较高的极化.从表面态的波函数出发就可以得到电子的自旋极化率.图3(a)中,A态和B态中自旋向上的组分分别为0.72和0.82.相反地,在C态和D态中,自旋向下的组分则分别达到了0.78和0.70的占比.大体上,我们可以说A态和B态有较高的自旋向上极化而C态和D态有较高的自旋向下极化.模型中同一个边界的两个态具有相反的传播方向和极化方向,这将形成螺旋状的边缘态分布,这类边缘态不携带电流但将有助于形成自旋流.
在图2(c)所示的能带结构中,我们已经说明,在合适的参数设置下,正方边心格子在1/3,1/2和2/3填充下都有完全打开的能隙,都能实现量子自旋霍尔效应.图4给出了系统在2/3填充下所对应的(部分)能谱以及边缘态的分布情况,相关参数的设置与图2(c)一致,vR=0.4,g=0.6,vSO=0.5.

图4 (网刊彩色)2/3填充下的正方边心格子 (a)带有费米能级的能谱(部分);(b)边缘态波函数分布Fig.4.(color online)(a)Energy spectra of Lieb lattice ribbons for a 2/3 fi led system,the Fermi level corresponds to four edge states;(b)wave-function distributions across the width for the edge states.
在图4(a)中我们标出了费米能级EF=1.125所对应的A,B,C,D四个边缘态,并在图4(b)中给出了这四个态的分布.在图2(c)中,对照我们设定的费米能级也可以看出当前的填充情况.在态A,B中,自旋向下的组分占到了相当大的比例,分别达到了0.93和0.64;而态C,D中则是自旋向上的组分占主导地位,分别为0.96和0.72.位于样品同一个边界的两个态A和C(B和D)具有相反的传播方向和自旋极化方向,这正是量子自旋霍尔效应的特征表现之一.计算此时系统的自旋陈数得到CS=1,这也证明此时的系统是量子自旋霍尔态.
一个小的技巧在于,当系统为2/3填充时,系统在费米能级的下方有四个价带波函数,这会增加计算自旋陈数的过程和难度,此时,我们可以转而计算费米面上方的两个导带波函数所对应的自旋陈数,其结果与价带波函数的结果相反,这将在一定程度上简化了计算的过程.在正方边心格子中,在恰当的参数设置下,当系统有图2(b)所示的能带结构时,改变系统的填充情况从1/3至1/2再到2/3的过程中,系统将经历从量子自旋霍尔态到半金属再到量子自旋霍尔态的转变.而当系统在一定参数下具有图2(c)所示的能带时,在这三种填充下,系统都将处于量子自旋霍尔态.需要指出的是,在时间反演对称破缺的情况下,两个反向传播的波函数之间存在一个微弱的背散射,自旋的输运过程总是伴随着一些能量损耗,这与时间反演对称保护下无耗散的自旋流还是有一些差别的.尽管如此,这一系统还是可以用在自旋注入等方面,在电子和自旋设备以及量子通信中有着潜在的价值和应用.
3 结 论
本文在Rashba自旋轨道耦合和交换场同时存在的情况下,详细研究和讨论了正方边心格子中的量子自旋霍尔效应.正方边心格子具有简立方对称性,每个原胞中包含三个不同的原子但其第一布里渊区中只含有一个狄拉克锥.我们的计算表明,在正方边心格子中,只有在内禀自旋轨道耦合不为零的情况下,第一布里渊区中M点的简并才能消除,从而得到一个完全打开的能隙,而这正是实现量子自旋霍尔效应的必要条件.借助于自旋陈数这一拓扑序以及边缘态和极化率等分析,我们发现在交换场破坏了系统时间反演对称的情况下,正方边心格子中依然能够实现量子自旋霍尔效应,虽然它和最初由Kane和Mele[11]提出的受时间反演对称保护的量子自旋霍尔效应有些微小的差别,但我们还是可以把这类现象归结为量子自旋霍尔效应,并受到自旋陈数的保护.
量子自旋霍尔效应在时间反演对称破缺的情况下仍然能够存在,这大大拓展了量子自旋霍尔效应的范畴,为借助磁场来控制量子自旋霍尔效应提供了理论依据和一个可能的模型基础.在表征量子自旋霍尔效应方面,自旋陈数比z2拓扑不变量具有更广泛的使用范围.自旋陈数不但适用于时间反演对称保护下的系统,其在时间反演对称破缺的情况下,仍然能够很好地表征类量子自旋霍尔效应.二维正方边心格子和三维立方边心格子在自然界中广泛存在[34].二维的Cu-O晶格就具有和正方边心格子类似的结构,研究者已经在其中实现了量子反常霍尔效应[36].边心格子最具有代表性的例子当属具有高居里温度的铜酸盐超导体(如YBa2Cu3O7和Bi2Sr2CaCu2O8)中的CuO2平面.
实验上,把K40或者Li6等单组分费米子放置在具有正方边心对称的格点上就可以实现类似的系统[37,38].当温度足够低时,这类原子之间的相互作用可以忽略不计,这时,我们在本文中所采用的紧束缚近似哈密顿量就可以成立[39,40].此外,如同目前已经实现的“人造石墨烯”[41],调节一个具有边心正方对称的二维电子气模型也有望实现人工的正方边心格子.二维冷费米气由于其良好的可操控性而被用来模拟许多其他的物理系统,最近人们已经在实验上实现了超冷原子体系中的自旋轨道耦合相互作用,这为研究多体物理提供了一个全新的方法和途径[42−44].图5给出了具有正方边心对称的冷费米子气体的部分能带图,可以看出相应的模型可以实现Majorana零模,这也为在实验上寻找Majorana费米子提供了一个潜在的模型,并且有望在量子信息和量子计算等领域发挥一定的作用.
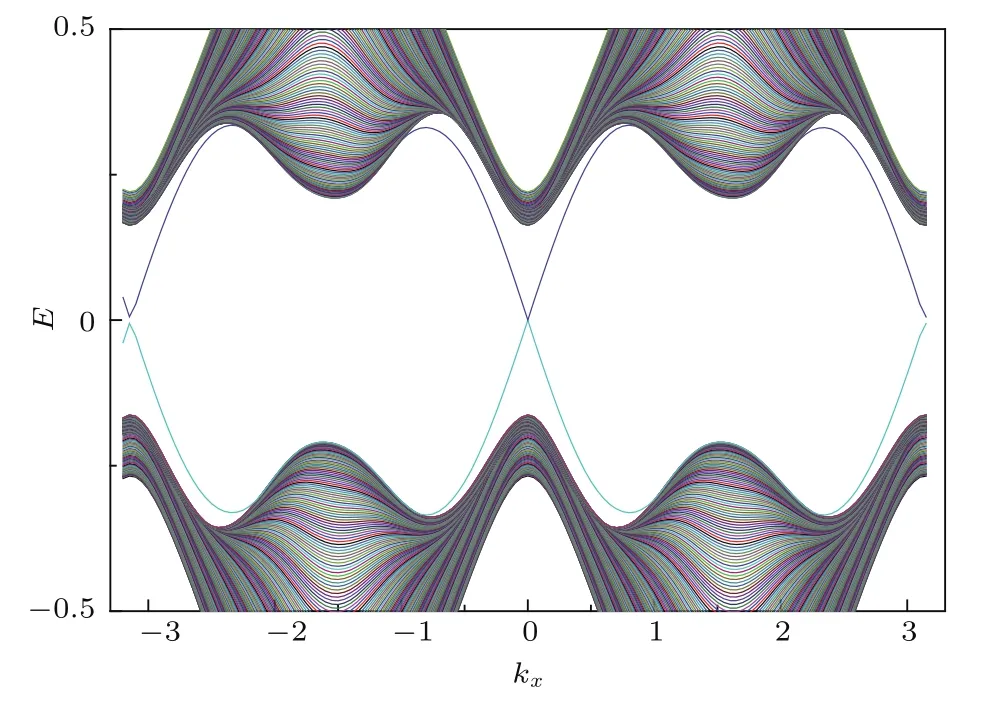
图5 (网刊彩色)具有正方边心对称的冷费米子气体中的Majorana零模Fig.5.(color online)Majorana zero modes in cold Fermi gas with a periodic potential possessing Lieb symmetry.
[1]Klitzing K V,Dorda G,Pepper M 1980 Phys.Rev.Lett.45 494
[2]Tsui D C,Stormer H L,Gossard A C 1982 Phys.Rev.Lett.48 1559
[3]Kane C L,Mele E J 2005 Phys.Rev.Lett.95 226801
[4]Zhang H J,Xu Y,Wang J,Chang K,Zhang S C 2014 Phys.Rev.Lett.112 216803
[5]Miao M S,Yan Q,van de Wall C G,Lou W K,Li L L,Chang K 2012 Phys.Rev.Lett.109 186803
[6]Zhang D,Lou W K,Miao M S,Zhang S C,Chang K 2013 Phys.Rev.Lett.111 156402
[7]Hasan M Z,Kane C L 2010 Rev.Mod.Phys.82 3045
[8]Qi X L,Zhang S C 2010 Physics Today 63 33
[9]Li Z J,Li Q,Chen Z G,Li H B,Fang Y 2014 Chin.Phys.B 23 028102
[10]Thouless D J,Kohmoto M,Nightingale M P,Den Nijs M 1982 Phys.Rev.Lett.49 405
[11]Kane C L,Mele E J 2005 Phys.Rev.Lett.95 146802
[12]Bernevig B A,Hughes T L,Zhang S C 2006 Science 314 1757
[13]Kon̈ig M,Wiedmann S,Brune C,Roth A,Buthmann H,Molenkamp L W,Qi X L,Zhang S C 2007 Science 318 766
[14]Sheng D N,Weng Z Y,Sheng L,Haldane F D M 2006 Phys.Rev.Lett.97 036808
[15]Yang Y Y,Xu Z,Sheng L,Wang B G,Xing D Y,Sheng D N 2011 Phys.Rev.Lett.107 066602
[16]Pradan E 2009 Phys.Rev.B 80 125327
[17]Qiao Z H,Yang S A,Feng W X,Tse W K,Ding J,Yao Y G,Wang J,Niu Q 2010 Phys.Rev.B 82 161414
[18]Haldane F D M 1988 Phys.Rev.Lett.61 2015
[19]Onoda M,Nagaosa N 2003 Phys.Rev.Lett.90 206601
[20]Liu C X,Qi X L,Dai X,Fang Z,Zhang S C 2008 Phys.Rev.Lett.101 146802
[21]Raghu S,Chung S B,Qi X L,Zhang S C 2010 Phys.Rev.Lett.104 116401
[22]Yu R,Zhang W,Zhang H J,Zhang S C,Dai X,Fang Z 2010 Science 329 61
[23]Wu C 2008 Phys.Rev.Lett.101 186807
[24]Guo H M,Franz M 2009 Phys.Rev.B 80 113102
[25]Zhang Z Y 2011 J.Phys.Condens.Matter 23 365801
[26]Ishizuka H,Motome Y 2013 Phys.Rev.B 87 081105
[27]Kargarian M,Fiete G A 2010 Phys.Rev.B 82 085106
[28]Chen W C,Liu R,Wang Y F,Gong C D 2012 Phys.Rev.B 86 085311
[29]Ohgushi K,Murakami S,Nagaosa N 2000 Phys.Rev.B 62 R6065
[30]Wang Z,Zhang P 2008 Phys.Rev.B 77 125119
[31]Shen R,Shao L B,Wang B,Xing D Y 2010 Phys.Rev.B 81 041410
[32]Beugeling W,Everts J C,Morais S C 2012 Phys.Rev.B 86 195129
[33]Zhao A,Shen S Q 2012 Phys.Rev.B 85 085209
[34]Weeks C,Franz M 2010 Phys.Rev.B 82 085310
[35]Sun K,Fradkin E 2008 Phys.Rev.B 78 245122
[36]He Y,Moore J,Varma C M 2012 Phys.Rev.B 85 155106
[37]Stanescu T D,Galitski V,Vaishnav J Y,Clark C W,Das Sarma S 2009 Phys.Rev.A 79 053639
[38]Zhu S L,Fu H,Wu C J,Zhang S C,Duan L M 2006 Phys.Rev.Lett.97 240401
[39]Bloch I,Dalibard J,Zwerger W 2008 Rev.Mod.Phys.80 885
[40]Goldman N,Urban D F,Bercioux D 2011 Phys.Rev.A 83 063601
[41]Gibertini M,Singha A,Pellegrini V,Polini M,Vignale G,Pinczuk A,Pfei ff er L N,West K W 2009 Phys.Rev.B 79 241406
[42]Zhang C,Tewari S,Lutchyn R M,Das Sarma S 2008 Phys.Rev.Lett.101 160401
[43]Chosh P,Sau J D,Tewari S,Das Sarma S 2010 Phys.Rev.B 82 184525
[44]Temari S,Sau J D 2012 Phys.Rev.Lett.109 150408
PACS:73.43.–f,71.70.Ej,73.61.–rDOI:10.7498/aps.66.127303
Time-reversal-symmetry broken quantum spin Hall in Lieb lattice∗
Geng Hu1)Ji Qing-Shan2)Zhang Cun-Xi1)Wang Rui1)†
1)(Department of Electronic Information Science and Engineering,Zhejiang Ocean University,Zhoushan 316022,China)
2)(Department of Donghai Science and Engineering,Zhejiang Ocean University,Zhoushan 316000,China)
8 December 2016;revised manuscript
17 April 2017)
In this paper,the time-reversal(TR)symmetry broken quantum spin Hall(QSH)in Lieb lattice is investigated in the presence of both Rashba spin-orbit coupling(SOC)and uniform exchange fi eld.The Lieb lattice has a simple cubic symmetry,and it has three di ff erent sites in each unit cell.The most distinctive feature of this model is that it contains only one Dirac-cone in the fi rst Brillouin zone,where the upper dispersive band and the lower dispersive band touch the middle zero-energy band at M point and form a cone-like dispersion.The intrinsic SOC is essentially needed to open the full energy gap in the bulk.When the intrinsic SOC is nonzero,all the band structures are separated everywhere in the Brillouin zone and can be characterized by some topological invariants.The exact QSH fi rst put forward by Kane and Mele in 2005 is characterized by the z2number.The protection from the TR symmetry ensures the gapless crossing in the surface state in the bulk gap.In our model,the presence of the exchange fi eld breaks the TR symmetry,which results in opening a small gap in the crossing point and the z2topological order is not suitable for the system.This kind of state is a TR symmetry broken QSH,which is characterized by the spin Chern numbers.The spin Chern numbers have a much wider scope of application than z2index.It is suitable for both TR symmetry system and the TR symmetry broken system.For Lieb lattice ribbons,the spin polarization and the wave-function distributions are obtained numerically.There exists a weak scattering between the counter-propagating states in the TR symmetry broken QSH,and the spin transport along the boundary with a low dissipation replaces the dissipationless spin current in a TR symmetry system.In experiment,such a system can be realized by the two-dimensional Fermi gases in optical lattice with Lieb symmetry.The above conclusions are expected to give theoretical guidance in the spin device and the quantum information.
quantum spin Hall e ff ect,spin-orbit coupling,topological order
10.7498/aps.66.127303
∗国家自然科学基金(批准号:11304281,10547001)和浙江省自然科学基金(批准号:LY13D060002)资助的课题.
†通信作者.E-mail:wangrui@zjou.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by National Natural Science Foundation of China(Grant Nos.11304281,10547001)and the Natural Science Foundation of Zhejiang Province,China(Grant No.LY13D060002).
†Corresponding author.E-mail:wangrui@zjou.edu.cn

