一类函数最值问题解法探究

安徽省枞阳县宏实中学(2467001) 江保兵

一类函数最值问题解法探究

安徽省枞阳县宏实中学(2467001) 江保兵

一道扑朔迷离的高考试题

例1. 已知函数f(x)=x2−2(a+2)x+a2,g(x)=−x2+2(a−2)x−a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A−B=( )

A.16 B.−16

C.a2−2a−16 D.a2+2a−16

这是2013辽宁高考理数试题第11题,此类问题涉及函数最小值的最大值或者最大值的最小值,绕来绕去,往往使学生不知所云.如何深入浅出地使学生理解这类问题的解法,进而掌握其背后蕴含的数学知识、数学方法和数学思想?如何通过此类试题的解决培养学生举一反三、深入思考的习惯,进而提升学生的解题能力助其形成新的知识结构?本文通过此类问题的几个典例,系统探讨了这类问题的解题方法,供大家参考.

破解方法之一:数形结合

解首先在画出f(x),g(x)的图像,如图1所示.再令f(x)=g(x),得到:x2−2ax+a2−4=0,x1=a−2,x2=a+2结合图像,由题意H1(x)≥f(a+2),H2(x)≤f(a−2).故A−B=f(a+2)−f(a−2)=−16,选(B).

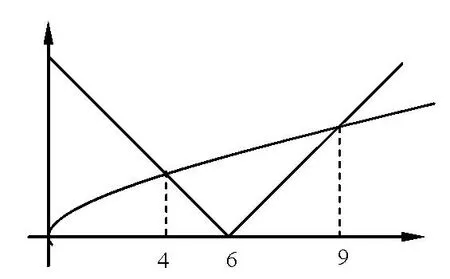
图2

图3

例2. (2011年清华大学保送生考试)求

解首先要搞清楚题意.表示函数|x−6|这二个函数中函数值较大的函数所构成的新的函数.问的是这个新函数最小值是多少?

读懂题意后,画出图像,如图2所示.M的最小值显然为2,此时对应的x=4.

破解方法之二:同向相乘

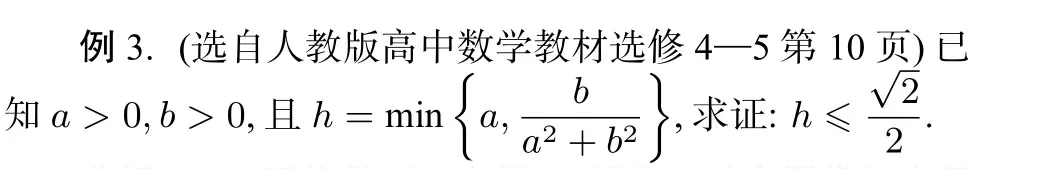
分析我们面临是两个变量,一元函数结合图像解决问题已经失效.这时必须改变解题方法,尝试用不等式的知识来解决问题.

总结例3和例4的方法:求min{max{f(x),g(x)}},当f(x)＞0,g(x)＞时,设M=max{f(x),g(x)},再利用M2≥f(x)×g(x)求解.

破解方法之三:同向相加

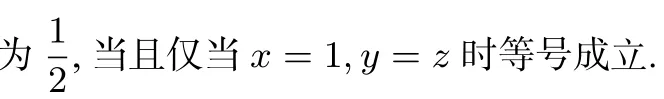
总结例5和例6的方法:求min{max{f(x),g(x)}},首先设M=max{f(x),g(x)},再利用2M≥f(x)+g(x)求解.事实上,方法二和方法三都是解决多元函数最小值的最大值问题的有力的武器,在许多场合中这二种方法是通用的,读者不妨试试.