地面瞬变电磁数据的早期畸变与校正方法

王 益，王 鹏

(1.中煤科工集团西安研究院有限公司，西安 710077; 2.长安大学环境科学与工程学院，西安 710054)



地面瞬变电磁数据的早期畸变与校正方法

王 益1，2，王 鹏1

(1.中煤科工集团西安研究院有限公司，西安 710077; 2.长安大学环境科学与工程学院，西安 710054)

地面瞬变电磁勘探实践中发现，不同边长外框采集的数据在早期存在规律性畸变,推断关断时间和视电阻率转换算法均有可能引起畸变,为此采用试验方法进行验证。通过计算证实：实际关断时间并不足以引发电磁数据畸变；而在常规情况下的早晚期时间节点均存在数据畸变，且畸变主要发生在节点前，畸变程度与回线大小正相关；采用晚期公式计算是导致畸变的主要原因。使用二分搜索法对试验数据进行视电阻率转换，可以有效的克服电磁数据的早期畸变，获得与实际地层更吻合的视电阻率曲线。对不同外框试验数据的计算表明校正效果随外框边长的增大而减弱。

瞬变电磁早期畸变；关断时间；早晚期节点；全区视电阻率；二分搜索法

0 引言

时间域瞬变电磁法由于其探测深度大、高阻穿透能力强、受地形影响相对较小和施工效率高的特点，已广泛应用于金属矿勘探[1]、油气田勘探[2]和煤田水文地质勘探[3～6]中。目前常用的装置介于大定源和中心回线之间，即在地面敷设较大的正方形发射回线，在回线中心1/3边长范围内进行数据采集，近似认为该区域为均匀场，电阻率转换按中心回线装置进行计算。

地面瞬变电磁数据采集中一个重要的参数是发射回线的大小，一般根据最大探测深度予以确定，但鲜见关于不同大小回线信号的研究。瞬变电磁观测信号分为早期和晚期，对早期信号响应特征的研究相对较少，杨海燕等[7]对多匝回线的自感影响早期信号的特征进行了研究，F.Kamenetsky等[8]从计算线圈自感的影响上分析早期信号的响应特性，李创社等[9]从仪器线路设计上研究早期信号的检测方法。常规地面瞬变电磁信号的视电阻率转换一般按晚期公式进行计算，这导致得到的早期视电阻率曲线畸变，与实际值偏差较大。由于瞬变场的表达式是电阻率和时间的隐函数，不能通过解析式从观测值得到岩层的视电阻率。在全区视电阻率计算方面，已有众多学者做了大量研究。白登海等[10]给出了一种时间域瞬变电磁法视电阻率的数值计算方法, 该方法根据中心方式磁场垂直分量时间变化率的核函数的表现特征, 把整个瞬变过程分为早期阶段、早期到晚期的转折点和晚期阶段。分别得到早期视电阻率和晚期视电阻率, 然后通过转折点构成一条完整的全程视电阻率曲线。杨生等[11]给出了中心回线装置发射电流为斜阶跃波形条件下全区视电阻率迭代反演计算方法。李建平等[12]把回线分解为水平电偶极子,然后给出利用电偶极子求取全区视电阻率的方法。王华军等[13]依据均匀半空间瞬变响应曲线随地下电导率、发射回线边长与观测时间具有平移伸缩特性, 提出了一种直接计算全区视电阻率的方法。付志红等[14]研究了斜阶跃场源瞬变电磁法的全程视电阻率数值计算。陈清礼基于[15]均匀半空间中心回线观测方式瞬变电磁测深法的感应电动势随电阻率的增大而单调下降的特性，设计出计算全区视电阻率的一种快速且精确的算法，张成范等[16]通过对理论模型和实际数据的计算证明了该方法的有效性和正确性。

地面瞬变电磁实际工作中发现，当采用不同边长的外框进行相同测点的测量时，相应的衰减值曲线存在有规律性的畸变。对边长越大的外框，转换的早期视电阻率值越高，但晚期均趋于一致。针对这种现象，在陕北某地进行针对性试验，以验证这种现象。从关断时间、早晚期节点与全区算法方面，对畸变现象进行了研究与校正。

1 早期畸变现象

大量实测结果表明，回线边长对视电阻率的影响较大。对同一测点进行瞬变电磁测深，其它参数不变，只改变回线大小，采集的衰减值曲线在早期相交，而视电阻率曲线在早期分叉。针对此现象，在陕北某煤田进行试验，图1为120、240、360m回线在相同测点观测的感应曲线和换算的视电阻率曲线，采取双对数坐标。

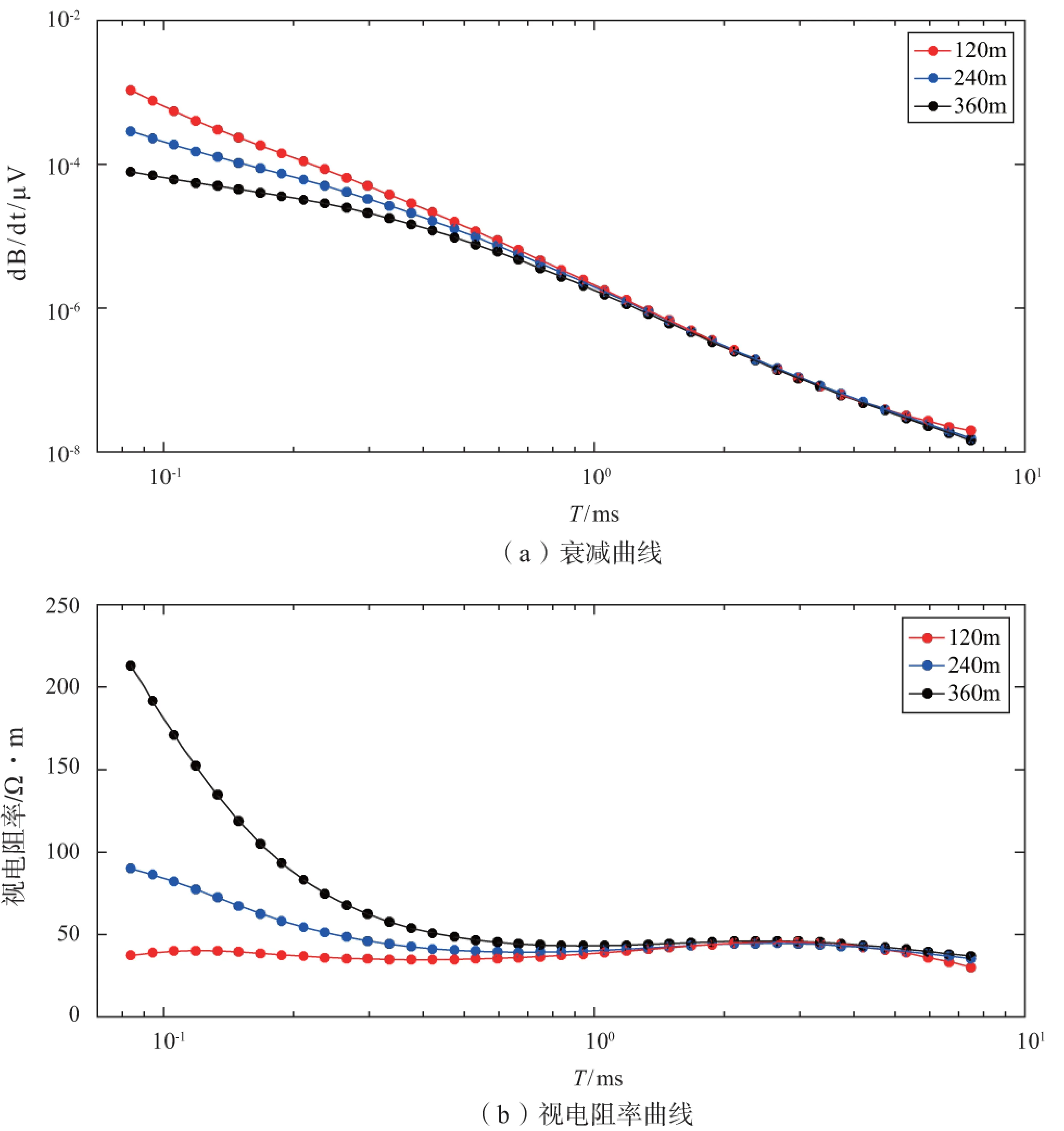
图1 不同大小回线观测结果Figure 1 Observed results from different sized loops

从图1可以看出，改变发射回线边长后，采集的感应曲线和换算的视电阻率曲线均存在明显不同。对感应曲线，表现为早期时间内大回线的感应值相对低，小回线的感应值相对高，即感应值与回线大小负相关；晚期时间差距明显缩小。对视电阻率曲线，晚期时间各曲线基本重合，而早期时间分叉加大，表现为回线越长则电阻率值越高。由瞬变电磁方法的特点可知，时间-视电阻率曲线反映地层深度上的导电性变化，而相同测点下地层导电性是唯一的，因此上面不同大框得到的结果并不统一这个特点与实际不符。

2 关断时间的影响

关断时间是影响早期信号的一个重要因素。由于完全断掉大框电流需要一定的时间，因此很容易地联想到是否因为外框越大越难关断，使其二次场受到影响而产生畸变。试验设备为V8工作站，关断时间的估算公式：

L=0.005×S1.127×N2

TΓ=I×L

式中L——电感，mH；S——发射框边长，m；N——发射框匝数；TΓ——关断时间，μs；l——发射电流，A。

试验中120、240、360m大框对应的电流分别是16A、13.7A、12.9A，按照上面公式计算关断时间分别为17.6μs、33.0μs、49.0μs。试验数据第一道时间为79.0μs，大于计算的关断时间，在忽略接收系统过渡过程对响应影响的条件下，可认为原始数据并没有受到关断时间的影响。

3 早晚期节点

薛国强[17]在对瞬变电磁视电阻率数据向平面波场测深视电阻率数据转换时，发现由于瞬变电磁使用晚期计算公式及装置问题, 使测深曲线早期数据发生畸变。在建立一个两层介质模型，使用不同大小的框进行正演计算，按晚期公式转换的视电阻率曲线所表现出来的规律，与试验数据相同。该项研究对这种现象的解释是：不同装置的早晚期时间界限不同，小框的早期时间相对较短，更早地进入晚期时间；大框的早期时间较长，进入晚期时间相对较晚。地表电阻率的相对高低也同样影响进入晚期时间的界限。对均匀半空间的正演结果表明，当接收时间段满足下式时，按晚期公式计算的视电阻率值与真值的偏差小于10%。

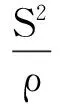
式中 t——晚期开始时间，ms； S——大框边长，m； ρ——地表电阻率，Ω·m。

针对目前常用的120、240、360、480、600、720、840、960m大框边长，分别计算出晚期开始时间t1、t2、t3、t4、t5、t6、t7、t8(表1)。

试验区地表电阻率约为100Ω·m，对试验数据进行晚期节点的计算，可得到120、240、360m大框在试验区进入晚期的时间节点，分别为0.1856、0.7425、1.6705ms。为验证晚期电阻率与真值的误差，分别将240m和360m晚期视电阻率曲线与120m曲线取比值，见图2。图中已将晚期节点标注在对应的曲线上，120m大框最早进入晚期，其次是240m外框和360m外框。由于120m外框最早进入晚期时间，节点后的曲线可近似视为真值。240m外框与360m外框在节点处的视电阻率比值均小于10%，说明实际数据表现的特征与理论计算一致。

以上分析表明，用晚期公式计算的瞬变电磁视电阻率曲线，在晚期节点之前畸变，使之与真值存在明显偏差。这种偏差在理论和实测数据上均表现与大框边长正相关的规律，且大框越长，畸变时间越长。

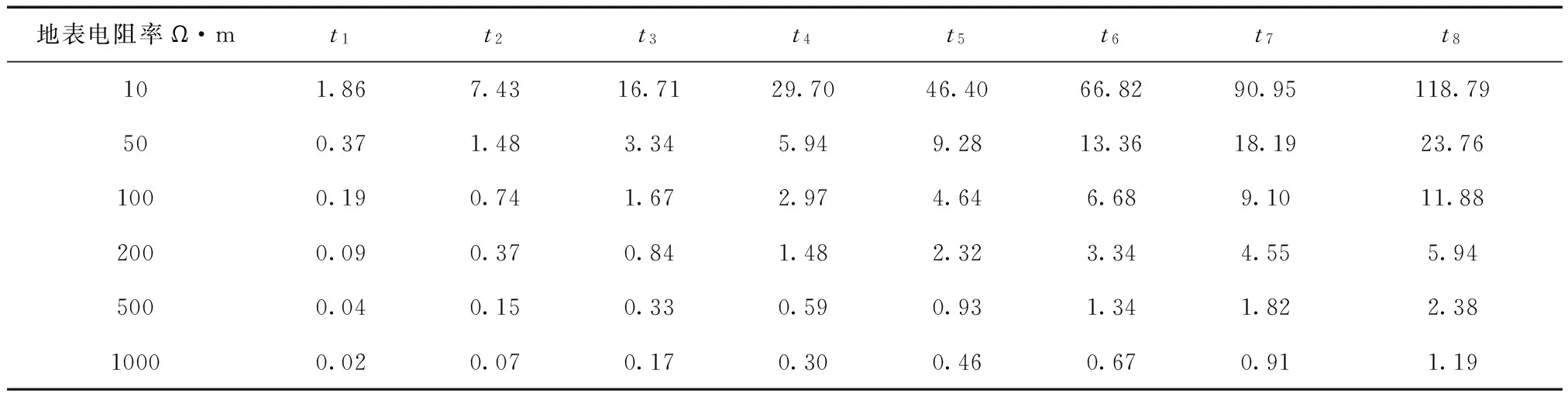
表1 晚期时间节点统计表

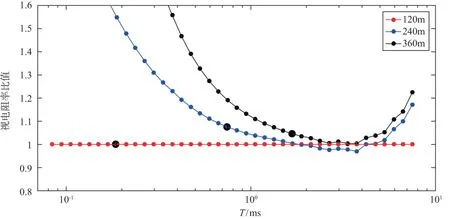
图2 不同大框视电阻率比值曲线与晚期节点Figure 2 Apparent resistivity ratio curves and late phase nodes from different sized loops

4 全区视电阻率计算实例

根据钻孔资料，试验区浅部为风积沙，中部为新近系红土，深部为延安组含煤地层(主要成分为中、粗砂岩)和三叠系永坪组粉、细砂岩。将钻孔测井曲线数字化，可得试验区岩层随深度的电阻率变化，见图3(a)。图3(a)为侧向电阻率测井曲线及其4阶拟合结果，该图显示由浅至深岩层电阻率逐渐升高，随后出现下降趋势，整体表现为“低-高-低”的地电断面。

采用陈清礼的二分搜索法[15]对试验数据进行

全区视电阻率计算。图3(b)(c)(d)分别为120、240、360m外框的晚期曲线和全区曲线。观察该图可以发现，120m外框数据在早期整体呈现最小电阻率；240m外框的早期曲线大幅下降，接近于最低阻；360m外框数据在早期也大幅下降，但整体仍为高阻，与实际值具有一定的偏差。总体而言，经过全区计算后，结果曲线在早期时间均有一定程度的下降，与真实值更趋于吻合。

需要注意的是，尽管使用二分搜索法得到的全区视电阻率曲线与实际更加吻合，但对不同的外框，得到的全区曲线并不一致，这说明该算法并不能完全解决全区视电阻率的转换问题。全区计算对早期电阻率计算不能完全恢复的原因在于，各全区计算方法均采用数值算法，公式推导中为便于计算，忽略一些影响因素(如过渡过程)，使得计算结果与真实值存在一定偏差，且不同算法的偏差并不相同。此处采用效果更好的二分搜索法，已对真实电阻率进行最大程度恢复。

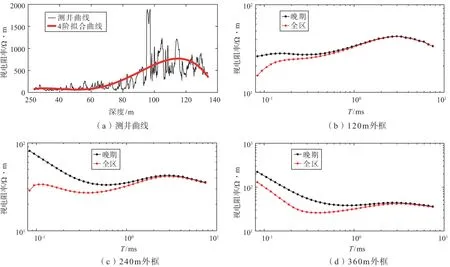
图3 测井曲线与不同大框电阻率曲线Figure 3 Logging traces and resistivity curves of different sized loops

5 结论

在发现不同边长外框得到的视电阻率曲线存在畸变后，展开针对性试验，在对试验数据分析、试算的基础上，对畸变原因、特征及校正方法进行总结，得出以下主要结论：

1)随着大框边长的加大，早期信号变弱。按晚期公式计算的电阻率曲线在早期明显畸变，表现为外框越大，早期电阻率值越高。

2)对关断时间的计算结果表明，各边长大框的关断时间均小于第一道采样时间。在忽略过渡过程影响的条件下，这种畸变现象与关断时间无关。

3)产生畸变现象的原因是在不适用的早期段使用晚期公式，早晚期时间节点与大框边长和地表电阻率有关。框越大、地表电阻率越低，早晚期节点越靠后。

4)使用全区算法能改善早期畸变现象。计算实例表明，二分搜索法转换的全区曲线与实际结果更吻合，但修正效果随框的加大而减弱。

[1]柳建新,刘春明,童艳光.强场源瞬变电磁仪及在某铜矿的试验性应用[J].物探与化探,2004,28(2):130-132.

[2]唐新功,胡文宝,严良俊，等.瞬变电磁法油藏动态监测模拟[J].石油物探,2004,43(2):192-196.

[3]周韬,韩自豪,周建雄，等. 瞬变电磁法在煤矿水害防治中的应用[J].中国煤田地质,2004,16(2):44-46.

[4]叶剑湘.瞬变电磁测深法找煤效果研究[J].中国煤田地质,2000,12(4):71-74.

[5]王惠亮.应用瞬变电磁法探测煤层风氧化带[J].采矿技术,2004,4(2):61-62.

[6]路军臣,苏维涛,张济怀.瞬变电磁法在探测小窑采空区中的应用[J].河北煤炭,2002,2:39-40.

[7]杨海燕,岳建华,胡文武，等.多匝回线的自感对瞬变电磁早期信号的影响特征[J].物探化探计算技术,2007.3:96-99.

[8]F.Kamenetsky and Chr.Oelsner. Distortions of EM transients in coincident loops at short-time-dalay[J]. Geophysical Prospecting, 2000, 48(6):983-993.

[9]李创社,李实,宋建平，等.瞬变电磁勘探法中早期信号的检测方法研究[J].煤田地质与勘探,1994,27(2):58.

[10]白登海,Meju M A,卢健，等.时间域瞬变电磁法中心方式全程视电阻率的数值计算[J].地球物理学报,2003,46(5):697-704.

[11]杨生.TEM中心回线法计算考虑关断时间的全区视电阻率[J].物探与化探,2003,32(6): 647-6511.

[12]李建平,李桐林,赵雪峰，等.层状介质任意形状回线源瞬变电磁全区视电阻率的研究[J]球物理学进展, 2007,22(6):1777-1780.

[13]王华军.时间域瞬变电磁法全区视电阻率的平移算法[J].地球物理学报,2008,51(6):1936-1942.

[14]付志红,孙天,陈清礼，等.斜阶跃场源瞬变电磁法的全程视电阻率数值计算[J].电工技术学报,2008,23 (11):15-211.

[15]陈清礼.瞬变电磁法全区视电阻率的二分搜索算法[J].石油天然气学报(江汉石油学院学报)，2009.4,31(2):45-49.

[16]张成范,翁爱华,孙世栋，等.计算矩形大定源回线瞬变电磁测深全区视电阻率[J].吉林大学学报,2009.7,39(4):755-758.

[17]薛国强,李貅.瞬变电磁测深早期数据的修正[J].地球物理学进展,2008.2,23(1):220-224

Surface TEM Data Early Phase Distortion and Calibration Method

Wang Yi1, 2, Wang Peng1

(1. Xi’an Research Institute, China Coal Technology and Engineering Group Corp, Xi’an, Shaanxi 710077;2. School of Environmental Science and Engineering, Chang’an University, Xi’an, Shaanxi 710054)

During the surface TEM prospecting practices, the early phase distortion can be found in data acquired from different sized loops have existed early phase regular distortions. It is inferred that the turn-off time and apparent resistivity conversion algorithm all can cause distortion, therefore, test procedure has been used to verify. Through computation has justified that the practical turn-off time is not enough to trigger electromagnetic data distortion. While under normal circumstances, early and late phase time nodes have data distortions, and mostly happened before the nodes; distortion degree is positively correlated with loop size; using late phase formula computation is the main reason to cause distortion. Through dichotomizing search carried out tested data apparent resistivity conversion, can effectively overcome early phase electromagnetic data distortion, obtained apparent resistivity curves are more accorded with actual strata. The computation of different sized loops tested data has shown that the calibrated effect is attenuating along with the increasing of loop size.

TEM data early phase distortion; turn-off time; early and late phase time nodes; region-dependent apparent resistivity; dichotomizing search

10.3969/j.issn.1674-1803.2017.06.15

1674-1803(2017)06-0074-05

王益(1982—)，男，四川人，工程师，在读硕士研究生，长安大学环境科学与土木工程学院地质工程专业，从事煤田电法实践与研究工作。

2017-04-01

文献标识码：A

责任编辑：孙常长