基于Pearson相关分析和回归分析方法的基金影响力研究
毛秀珍,章璐杰,毛天翔,王友钊,黄 静
(1.浙江省科技信息研究院,杭州 310006;2.浙江大学生物医学工程和仪器科学学院,杭州 310007;3.浙江理工大学信息学院,杭州 310018)
基于Pearson相关分析和回归分析方法的基金影响力研究
毛秀珍1,章璐杰2,毛天翔3,王友钊2,黄 静3
(1.浙江省科技信息研究院,杭州 310006;2.浙江大学生物医学工程和仪器科学学院,杭州 310007;3.浙江理工大学信息学院,杭州 310018)
通过Pearson相关分析和回归分析方法评估基金资助和基金项目诸项指标的影响关系,较全面地反映了基金使用的效果。研究结果显示,不同额度的基金资助对经济投入、经济效益、社会效益、科技效益和企业自身发展具有不同的影响力。研究结果表明,结合相关分析与回归分析的方法可以对基金影响力进行比较有效的评估。
基金;影响力;Pearson相关分析;评估;回归分析
一、影响力评估和描述方法
(一)Pearson相关分析
在统计学中,皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,PMCC),用来度量两个变量X和Y之间的相互关系,取值范围介于-1和+1之间[5]。皮尔逊相关系数在学术研究中被广泛应用来度量两个变量线性相关的强弱。两个变量之间的皮尔逊相关系数定义为这两个变量的协方差与二者标准差积的商,即:
(1)
式(1)定义了总体相关系数ρXY。若用样本计算的协方差和标准差代替总体的协方差和标准差,则为样本相关系数,一般用r表示:
(2)
另一个与式(2)等效的相关系数定义,通过标准化以后变量均值的积定义。假设样本可以记为(Xi,Yi),则样本Pearson相关系数为:
(3)

本文利用Pearson相关分析方法,对基金资助与基金各项指标之间的相关系数进行计算,根据相关系数的大小确定两者之间线性关系的强弱,通过线性关系的强弱对基金资助与基金各项指标之间的影响力进行评估和排序。
(二)回归分析
回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法[6-7]。回归分析按照涉及的变量的数量,分为一元回归和多元回归分析[6-8]。按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
回归分析是应用广泛的数据分析方法之一。它基于观测数据建立变量间适当的依赖关系,以分析数据内在规律,并可用于预测和控制等问题[9-10]。处理非线性回归的基本方法是,通过变量变换,将非线性回归化为线性回归,然后用线性回归方法处理。假定根据理论或经验,已获得输出变量与输入变量之间的非线性表达式,但表达式的系数是未知的,要根据输入输出的n次观察结果来确定系数的值。按最小二乘法原理来求出系数值,所得到的模型为非线性回归模型。
本文利用回归分析,得到基金资助与基金各项指标之间的函数关系,利用函数关系对基金资助与基金各项指标之间的影响力进行描述,根据参数和图表寻找函数的拐点,得出在有限基金资助的情况下以各方面指标达到相对最佳效果为目的的最优基金资助额度。
二、实证研究:影响力评估和描述
(一)数据来源与指标选取
本文希望通过对浙江省科技型中小企业创新基金影响力的实证研究,得出创新基金资助和创新基金各方面指标的相关系数和函数关系,验证相关分析和回归分析方法是否可以有效地应用于政府性基金的影响力评估和描述。采用的样本来自于2006—2013年浙江省科技型中小企业创新基金(以下简称创新基金)项目的1780项验收信息,统计每年的总体情况作为分析数据。
创新基金属于政府性基金,关注的主要有两方面:一方面是基金资助带引的资金投入;另一方面是基金资助项目的各方面效益,包括经济效益、科技效益、社会效益以及企业自身发展等四方面效益。因此一级指标定为带引资金投入、经济效益、科技效益、社会效益和企业自身发展。在验收信息中选取具体的二级指标进行分析。基金的资助有利于激励企业增加研发投入的资金,选取项目总投资表示带引资金投入的二级指标。项目的经济效益可以通过产值和利润衡量,选取项目总销售额和总净利润表示经济效益的二级指标。项目的科技效益是项目科研创新能力的直接反映,选取项目总专利数表示科技效益的二级指标。项目的社会效应往往从解决就业和缴纳税收体现,选取项目总交税额和总增加就业人数表示社会效益的二级指标。企业自身发展可以通过企业规模来衡量,选取总企业规模表示企业自身发展的二级指标。
(二)基于相关分析的创新基金影响力评估
采用Pearson相关分析方法,利用SPSS19.0统计分析软件对创新基金资助和项目总投资、总销售额、总净利润、总专利数、总交税额、总增加就业人数和总企业规模等二级指标的相关性进行计算,结果如表1所示。

表1 创新基金资助和七项二级指标的Pearson相关性
注:**在0.01水平(双侧)上显著相关,*在0.05水平(双侧)上显著相关。
创新基金资助与项目总投资的相关系数为0.966,在0.01水平上显著,两者有明显的线性关系,创新基金资助对项目总投资有明显的带引作用。创新基金资助与代表项目经济效益的总销售额和总净利润的相关系数为0.964和0.825,分别在0.01水平和0.05水平上显著,创新基金投入与企业经济效益有比较明显的线性关系。创新基金资助与代表项目科技效益的总专利数的相关系数为0.947,在0.01水平上显著,有明显的线性关系,创新基金投入能促进项目科技效益。创新基金资助与代表项目社会效益的总交税额和总增加就业人数的相关系数为0.929和0.969,均在0.01水平上显著,创新基金资助对企业社会效益有明显的线性关系。创新基金资助与企业自身发展的相关系数为0.927,在0.01水平上显著,创新基金资助对企业自身发展有明显的线性关系。
Person相关系数越接近1,表示线性关系越强,即表明基金资助对该项指标具有更强的影响力。影响力评估采取这样的规则,如果一级指标具有多项二级指标,则选取二级指标中绝对值最小的相关系数作为一级指标的相关系数。据此将创新基金资助对带引资金投入、经济效益、科技效益、社会效益和企业自身发展五个一级指标的影响力进行排序:带引资金投入0.966>科技效益0.947>社会效益0.929>企业自身发展0.927>经济效益0.825。创新基金资助最能促进企业对项目的资金投入,具有非常优秀的带引作用;创新基金资助在项目科技效益、社会效益和企业自身发展方面的影响力非常明显且依次减弱,都具有很好的促进作用;创新基金资助对经济效益的影响力方面虽然不及以上四项,但是从相关系数上看仍具有一定的线性关系,说明也具有较好的促进作用。
(三)回归分析
对两个变量进行回归分析,描述变量之间关系最合适的模型不一定是线性模型。如果在具体问题的分析中只使用线性回归的方法进行研究,将无法得出正确的结论,也不能分析出客观的实际情况。本文同时对基金资助和七项二级指标进行线性和非线性回归分析,选择最适当的回归模型。可以从相对简单的二次回归和三次回归中选择一种进行非线性回归分析,二次回归只有一个拐点,结合现有数据的特点,可能存在不止一个拐点的情况,因此选用三次回归分析更加合适。
对创新基金资助和项目总投资、总销售额、总净利润、总专利数、总交税额、总增加就业人数和总企业规模等七项二级指标进行线性和三次回归分析,分别以项目总投资、总销售额、总净利润、总专利数、总交税额、总增加就业人数和总企业规模为因变量,以创新基金资助为自变量,结果如表2和图1—7所示。
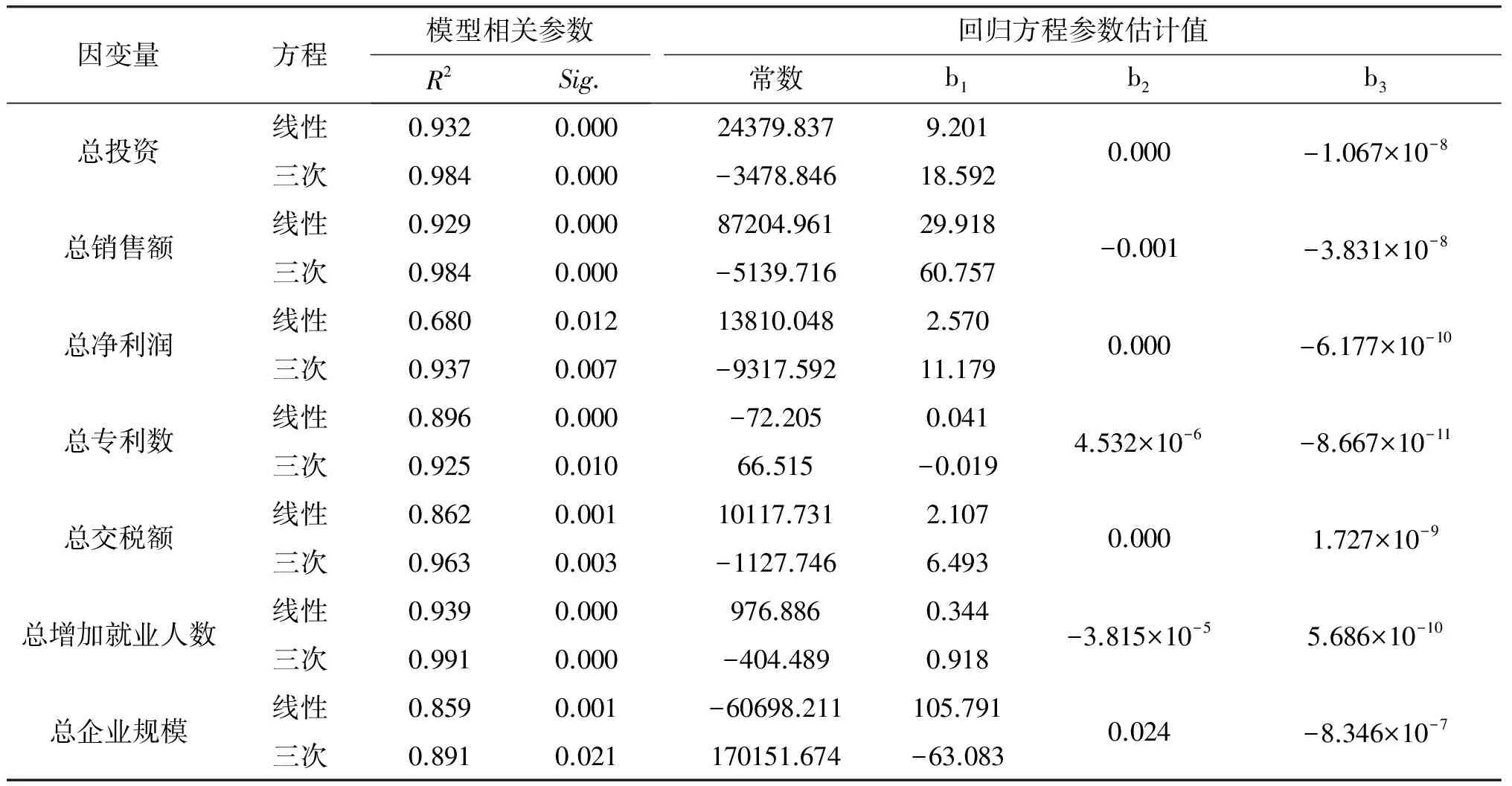
表2 七项二级指标关于创新基金资助的回归分析的模型相关参数和参数估计值
表2中参数R2表示回归模型的解释程度,越大解释程度越高,参数Sig.表示F检验的P值,越小越显著。线性回归模型和三次回归模型两个参数差别不大,有时互有优劣,不能简单地通过参数比较确定合适的模型,需要结合回归曲线图观察得出哪个模型更合适。当三次函数出现明显拐点的时候,通过对表2中参数估计值表示的回归方程求导可以得出拐点处的总基金资助额度。根据图1-7的三次和线性回归曲线和数据点的吻合程度选择回归模型,结合拐点处的总基金资助额度,可以得出以下结论:
a)三次曲线比线性曲线更适合描述基金资助与资金投入(项目总投资)、经济效益(总销售额和总净利润)以及社会效益(总交税额和总增加就业人数)之间的关系。总体上说,总投资、总销售额、总净利润、总交税额和总增加就业人数随着基金资助的增加而增加,小于1.5亿元时基本是线性增加,大于1.5亿元时增加不明显甚至有小幅减少。在一定资助额度的情况下,基金资助对这几项二级指标的影响是线性的,具有很强的影响力,但是当资助额度大于1.5亿元时,基金资助的影响不大,影响力减弱。
b)三次曲线比线性曲线更适合描述基金资助与科技效益(总专利数)之间的关系。总体上说,总专利数随着基金资助的增加而增加,小于0.5亿元时增加不明显,大于0.5亿元时增加明显。在资助额度较少的情况下,基金资助对总专利数的影响力不大,但是当基金资助大于0.5亿元时,基金资助对总专利数的影响是线性的,具有很强的影响力。
c)线性曲线比三次曲线更适合描述基金资助与企业自身发展(总企业规模)之间的关系。整个趋势是总企业规模随着基金资助的增加而增加,影响是线性的,一直具有很强的影响力。

图1 总投资关于创新基金资助的线性和三次回归曲线
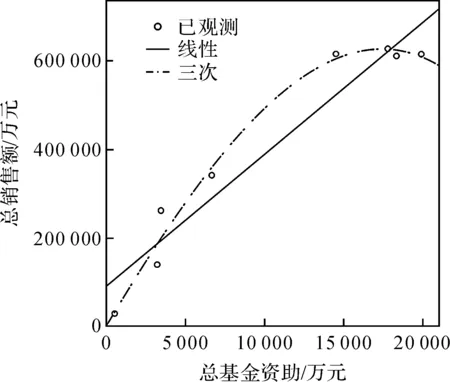
图2 总销售额关于创新基金资助的线性和三次回归曲线
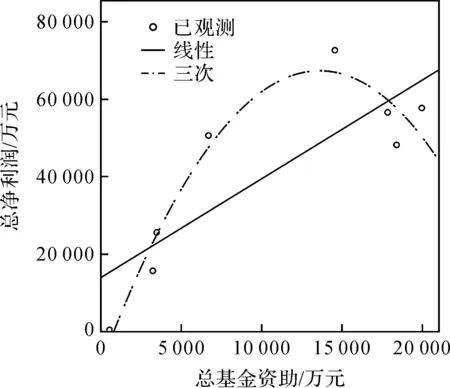
图3 总净利润关于创新基金资助的线性和三次回归曲线
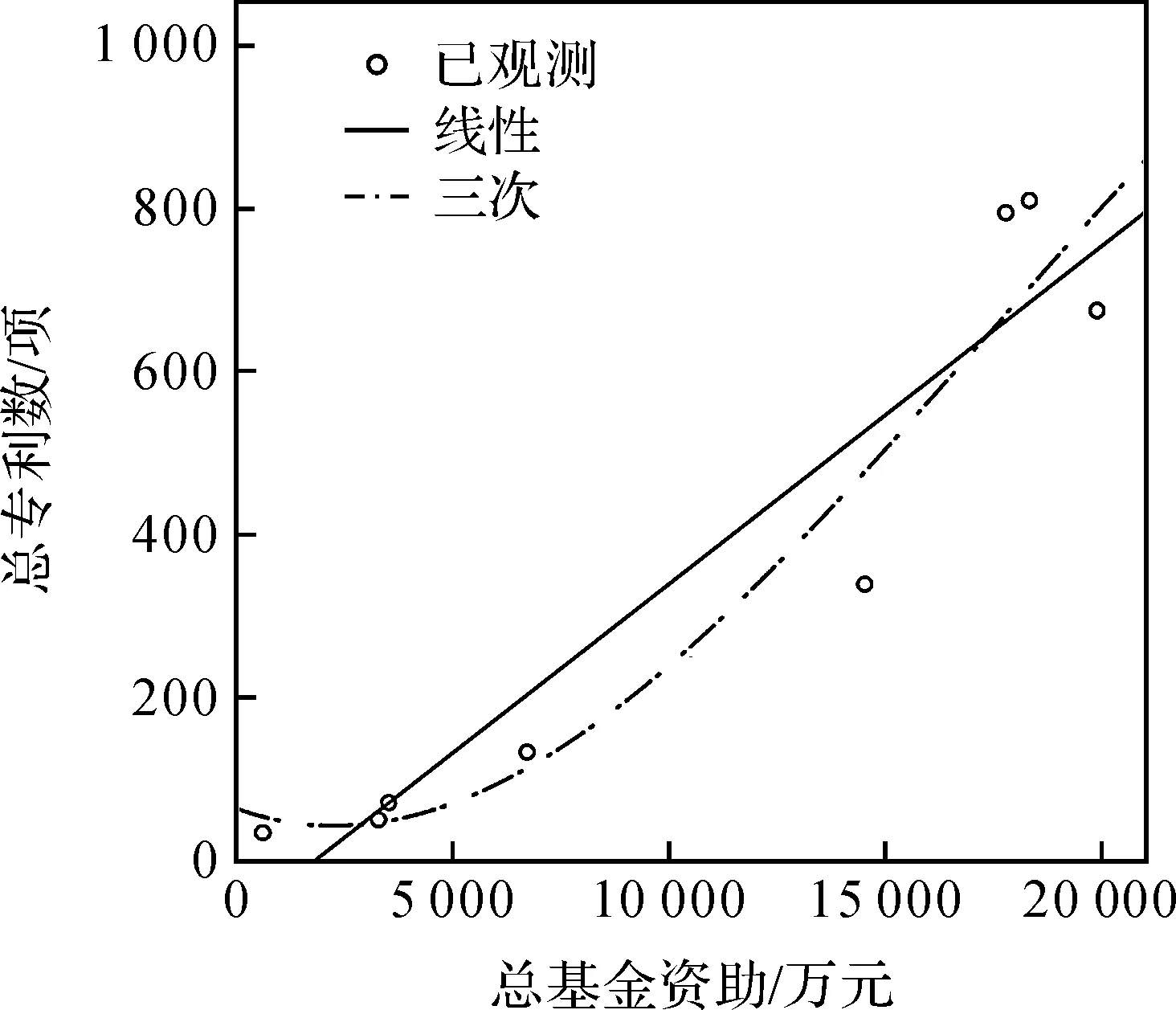
图4 总专利数关于创新基金资助的线性和三次回归曲线
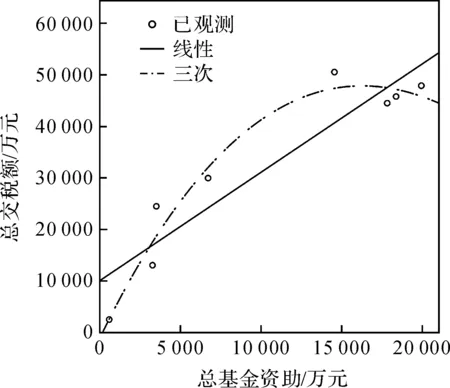
图5 总交税额关于创新基金资助的线性和三次回归曲线
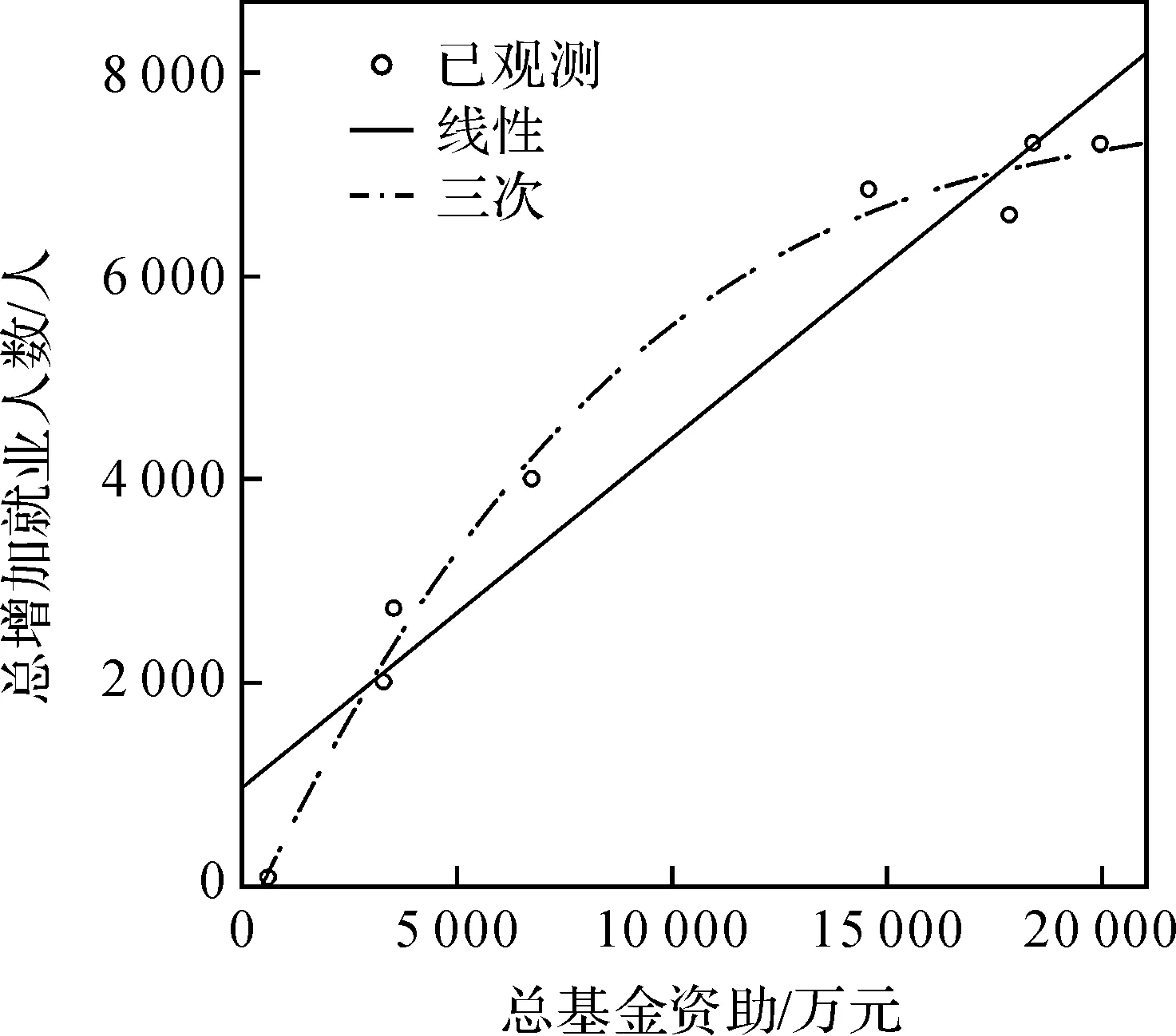
图6 总增加就业人数关于创新基金资助的线性和三次回归曲线
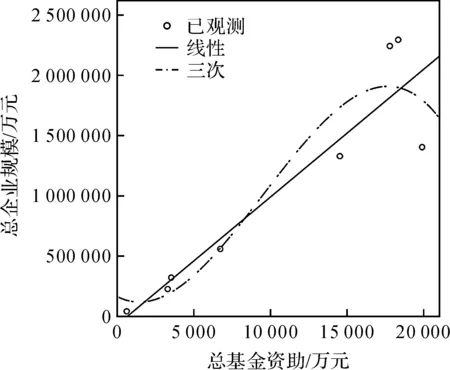
图7 总企业规模关于创新基金资助的线性和三次回归曲线
三、研究结果分析及建议
当总基金资助小于一定数额时,基金资助对经济投入、经济效益、社会效益的影响近似线性,基金资助是主要影响因素,具有很强的影响力,在总基金资助大于一定数额时,影响不明显。在总基金资助小于一定数额时,基金资助对科技效益的影响不明显,在总基金资助大于一定数额时,影响近似线性,基金资助是主要影响因素。基金资助对企业自身发展的影响在样本范围内是靠近线性的,基金资助是主要影响因素。
根据研究结果结合基金资助额度是有限的现实情况对创新基金提出以下几个建议:
a)如果创新基金对经济投入、经济效益、社会效益的影响比较重视,当基金资助大于1.5亿元/年时,不太需要考虑通过提高基金资助额度的方式提高经济投入、经济效益、社会效益。
b)如果创新基金对科技效益的影响比较重视,基金资助大于0.5亿元/年时,基金资助额度对科技效益具有很强的影响力,可以考虑通过提高基金资助额度的方式提高科技效益。
c)如果创新基金对企业自身发展的影响比较重视,可以考虑通过提高基金资助额度的方式促进企业自身发展。
四、结 语
创新基金资助对基金项目经济投入、经济效益、社会效益、科技效益和企业发展五方面均具有一定的影响力,结合研究结果和建议发现基金资助总额在1.5亿元时可以兼顾五方面的需求,达到相对最优的状态。实证研究表明,相关分析及回归分析方法,能够对政府性基金在资金投入、经济效益、科技效益、社会效益和自身发展的影响力作出合适的评估、描述,得出客观、完整的分析结论。本文认为相关分析及回归分析方法可以客观、高效地应用于基金的影响力研究。
[1] 皇甫伟.SPSS相关分析与线性回归分析在英语考试成绩分析中的应用[J].中国电力教育,2007(10):52-53.
[2] 朱跃龙,朱佳丽,李士进,等.基于相关分析和回归模型的引江济太水量水质关系分析[J].微电子学与计算机,2012, 29(3):47-50.
[3] 赵鹏,夏北成,秦剑桥,等.流域景观格局与河流水质的多变量相关分析[J].生态学报,2012,32(8):2331-2341.
[4] 焉晓贞,谢红,王桐.一种基于相关分析的多元回归数据估计方法[J].沈阳工业大学学报,2013,52(2):212-217.
[5] 杜秀英.基于Pearson相关分析的期刊引用关系研究[J].科技文献信息管理,2012,(2):18-23.
[6] 胡健颖,冯泰.实用统计学[M].北京:北京大学出版社,2002:240-303.
[7] 薛毅.数学建模基础[M].北京:工业大学出版社,2004:292-308.
[8] 薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007:314-327
[9] 田兵.多元线性回归分析及其实际应用[J].阴山学刊,2011,25(1):16-19.
[10] WEISBERG S. Applied Linear Regression[M].Hoboken:Wiley,2005:21-68.
(责任编辑: 钱一鹤)
Research on the Influence of Fund Based on Pearson Study of Fund Influence Based on Pearson Correlation Analysis and Regression Analysis Method
MAOXiuzhen1,ZHANGLujie2,MAOTianxiang3,WANGYouzhao2,HUANGJing3
(1.Zhejiang Institute of Scientific and Technological Information, Hangzhou 310006, China; 2.College of Biomedical Engineering and Instrument Science, Zhejiang University, Hangzhou 310007, China; 3.School of Information, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Pearson correlation analysis and regression analysis method were used to evaluate the relationship between the fund assistance and the indices of fund projects which comprehensively reflected fund use effect. The research results show that fund assistance with different limit has different influence on economic input, economic benefit, social benefit, technical benefit and enterprise development. The research results indicate that correlation analysis and regression analysis method can effectively evaluate the influence of the fund.
fund; influence; Pearson correlation analysis; evaluation; regression analysis
10.3969/j.issn.1673-3851.2017.08.004
2016-11-29 网络出版日期: 2017-05-24
毛秀珍(1957—),女,浙江慈溪人,研究员,学士,主要从事科技统计与软科学方面的研究。
F224
A
1673- 3851 (2017) 04- 0306- 06
和
各方面指标之间的相关关系和函数关系,在一定程度上可以评估和描述基金资助和基金项目各方面指标之间的影响关系。本文通过Pearson相关分析得到基金资助和基金指标的相关系数,利用相关系数对影响力进行评估,通过回归分析得到基金资助和基金各方面指标的函数关系,利用函数关系对影响力进行描述。
影响力研究能够较全面地反映基金使用效果和意义。利用相关分析和回归分析方法对变量之间的关系进行研究是比较常用的方法。皇甫伟[1]将相关分析和回归分析方法应用于英语成绩的分析,建立英语成绩分析模型,可以直观、高效、客观地对学生英语考试成绩进行分析。朱跃龙等[2]将相关分析和回归分析方法应用于引江济太工程的水量水质关系分析,根据相关分析结果,建立初始水质情况与达标时所需饮水量之间的关系模型,并建立不同情况下的回归模型,通过比较选取最终模型,以保证水质水量关系模型的正确性。赵鹏等[3]将多变量相关分析应用于流域景观格局与河流水质的分析,明确影响水质变化的关键景观因素,为深入了解景观对水质的影响机制提供重要的研究价值。焉晓贞等[4]对无线电传感器网络数据进行相关分析的多元线性回归分析,提出了一种基于相关分析的多元回归数据估计方法,用来解决无线传感器网络中数据估计方法存在输入变量较多,估计计算复杂度较高和估计效率低等问题。由现有文献可知,相关分析和回归分析方法在广泛的领域已有比较成熟的应用。

