电偶极子的各向异性辐射特性

李瑾，冯晓毅，王明军

（1.陕西学前师范学院计算机与电子信息系，西安710100；2.西北工业大学电子工程学院，西安710072；3.咸阳师范学院电子工程学院，陕西咸阳712000）

电偶极子的各向异性辐射特性

李瑾1,2，冯晓毅2，王明军3

（1.陕西学前师范学院计算机与电子信息系，西安710100；2.西北工业大学电子工程学院，西安710072；3.咸阳师范学院电子工程学院，陕西咸阳712000）

目的研究均匀各向异性介质中电磁源的辐射特性及其规律。方法基于电磁场的方向多长度标准理论，建立各向异性介质中标量势的达朗伯方程，求解微分方程得到推迟形式的标量势和矢量势的解析表达式，通过与现有文献比较验证该表达式正确性。结果得到了电各向异性介质中电偶极子的辐射电磁场，当介质为各向同性介质时，所得辐射场与现有文献完全一致，数值仿真了电偶极的辐射特性和结果的物理机制。结论在各向异性介质中，电偶极的辐射特性具有各向异性特性，在某一方向观测时，与该方向垂直方向的介电常数越大，辐射越强。为各向异性介质如磁化等离子体等介质中雷达、天线的工程优化设计提供了理论基础。

电磁辐射；电偶极子；多尺度理论

随着电子科技应用的不断进步，各向异性介质中如磁化等离子体、晶体以及复合介质等越来越多的光电磁问题受到国内外学者及国防等的普遍关注，得出这些介质中电磁源的解析表达式显得尤为重要。这一表达式的获得不仅是完善电磁场理论本身发展的需要，而且在各向异性介质中目标识别、雷达天线等领域有着重要的应用前景。在这一研究领域，N.P.Zhuck在四维空间得到独立于坐标的格林函数[1]，各向异性介质中的并矢格林函数十分有用，提供了获得该介质中电磁场的简便方法[2]。在某些各向异性介质的空间域上，人们对精确封闭形式的格林函数进行了较为详细的研究[3]。同时，旋光双轴各向异性介质、具有仿射变换的单轴双各向异性介质以及轴向双各向异性介质中的格林函数已被详细地描述[4—8]。实际上，基于国际单位制，国内外学者在各向异性介质中电磁波的辐射、传播等方面做了许多有意义的探索。一种创新性的理念——多长度在不同的方向进行不同的伸缩提出以后，被证实可以将均匀各向异性介质变换为均匀的各向同性介质，可以进行目标整形，如将椭圆柱体整形为圆柱体。在将这一多长度标准应用与研究各向异性介质时，必须研究电磁场理论的多长度标准变换及其应用[9]。以文献[10]为基础，当等离子体球的半径远小于入射电磁波的波长时，人们获得了等离子体球内外的电磁场表达式[11]。基于电磁场的多长度标准变换理论，位于平面电磁波照射和波束照射下，一个各向异性均匀介质球内外的电磁场得到了详细的研究[12—13]，进而人们获得了均匀各向异性介质球的瑞丽散射特性，并做了仿真与分析[13]。因此，各向异性介质中电磁波的传播、目标散射及其电磁源的辐射受到国内外学者的普遍关注。

文中所讨论的内容是文献[10—14]中各向异性电磁问题的扩展与延伸，主要贡献有以下几点：获得了电各向异性介质中的d′Alembert方程；提出了各向异性介质中的洛伦兹规范；利用电磁场的多长度标准理论将各向异性介质中的非齐次波动方程重构为各向同性介质空间的非齐次波动方程；获得了各向异性介质中矢量磁位和标量电位的推迟势表达式。整篇文章中电磁场的时间因子采用ejωt且予以忽略，矢量用黑斜体表示，矢形式的介电常数设为ε=ε0(ε11e1e1+ε22e2e2+ε33e3e3)，其中ei(i=1,2,3)为笛卡尔坐标系中的单位矢量。

1 各向异性均匀介质中的光电辐射场

1.1 电各向异性介质中标量势的达朗伯方程

在一般坐标系中，无耗均匀各向异性介质的电磁参数如果用矩阵描述将是一个对称矩阵，例如介电常数张量可以表示为：

利用矩阵知识可以获得上式的三个特征矢量和三个特征值λ1，λ2，λ3，选择该三个特征矢量作为新坐标系的单位矢量。为方便起见，称这一新的坐标系为主坐标系。在主坐标系中，上式变为：

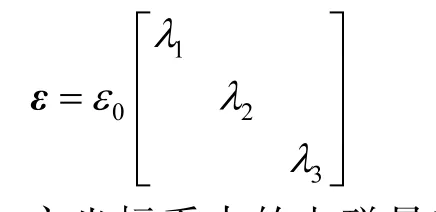
主坐标系中的电磁量和一般坐标系中的电磁量可用特征矢量加以转换，因此只需研究主坐标系中的达朗伯方程。为了习惯上的方便，仍将λ1，λ2，λ3表示为λ1→ε11，λ2→ε22，λ3→ε33。设主坐标系中电磁参数的并矢为：

介质中电磁源和电磁场所满足的微分方程，具体为：

上述方程是研究各向异性介质中辐射场的基础。由于▽·B=0，所以，可以令：

式中：A称为矢量磁位，一般情况下是空间位置和时间的函数。将式（2）代入式（1）的第二式可得：

由于式（3）的获得未涉及介质的电磁参数，所以对各向异性介质有效，具有规范不变性。其中φ称为标量电位或标量势。将式（2）、（3）的电场强度与电位移矢量的关系代入式（1）的第一式可得：

其中εr=ε11e1e1+ε22e2e2+ε33e3e3，称为并矢形式的相对介电常数。式（4）为标量电位和矢量磁位耦合的微分方程，求解十分困难，幸运的是矢量磁位A的旋度已确定，但其散度没有给定，为简化式（4）提供了可能，只要提出合理的散度规范，就可以进行简化。各向同性介质空间，由于麦克斯韦方程仅给出了矢量势A的旋度，没有确定该矢量势的散度。洛伦兹基于此提出了各向同性介质空间的规范已经被证明在简化达朗贝尔方程方面很有用，并具有明显的物理意义，但该规范不适应于各向异性介质空间。在各向异性介质空间，矢量势的散度与标量势的关系必须满足：等式两端在量纲上相等；包含了各向同性介质空间的洛伦兹规范。为此，提出以下各向异性介质空间的规范[15]，具体为：

方程（5）变为：

式（6）是各向同性介质空间的洛伦兹规范，也表明了提出的各向异性介质空间规范式（5）的有效性。利用式（5）和（4）可得：

1.2 标量势和矢量势的时谐解

将式（7）和各向同性介质中的非齐次微分方程进行比较，不难发现，求解式（7）的困难在于空间导数前面的系数εii的存在。为此，可引入方向长度多标准坐标系'∑，令其长度关系为：

方程（7）将变为：

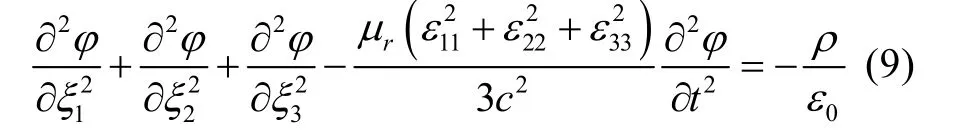
应注意的是式（9）中的标量势和电荷分布是在主坐标系中给出的。为了简单起见，研究时谐场，设时间因子为ejωt，ω为角频率。由文献[10—11]可得：

将式（10）、（11）代入式（9），得到：

利用格林公式和Sommerfeld辐射条件，可得方向长度多标准坐标系中标量势的解为：

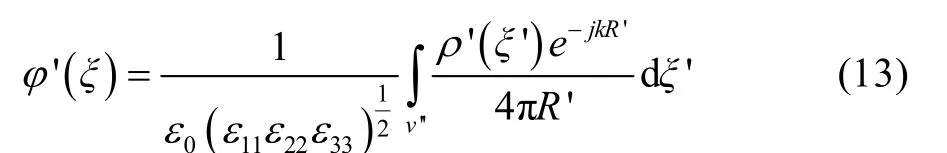
利用方向长度多标准坐标系和主坐标系电磁参量的变换关系可得主坐标系中标量势的表达式：

利用式（5）和麦克斯韦方程可得矢量磁位表达式：

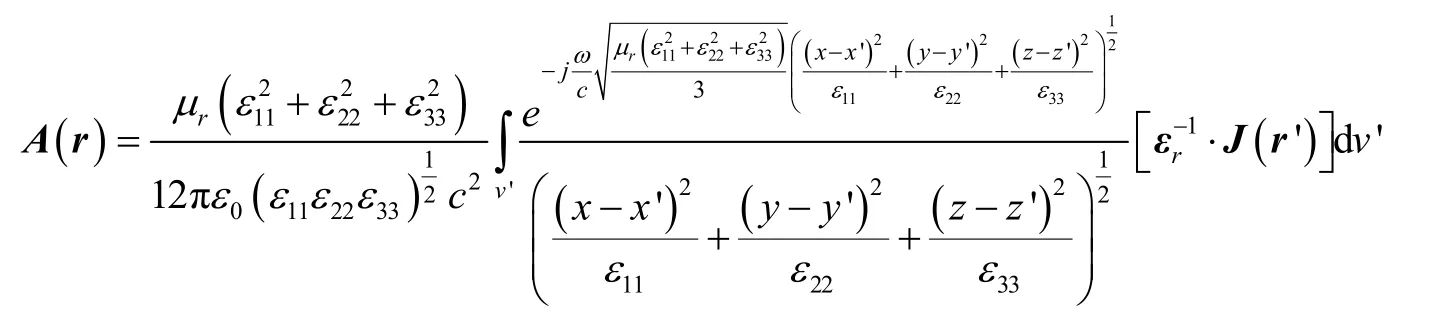
由此可以看出，相对磁导率仅对标量势的相位有贡献，对幅度大小没有贡献。除此之外，矢量磁位的大小正比于相对磁导率，且是介电常数并矢的复杂函数。如果所得各向异性介质中结果正确，应包含各向同性均匀介质中矢量磁位和标量电位的解析表达式。当εii=εr(i=1,2,3)，介质将变为各向同性电介质，将其代入式（14）、（15）可得：

显然，上述结果与现有电磁场理论所得各向同性介质空间矢量磁位和标量电势的时谐表达式完全一致，说明了式（14）、（15）的正确性。

1.3 电偶极子辐射场

前面得出了电各向异性、磁各向同性介质中电磁源的矢量磁位A和标量电势φ，因此，由麦克斯韦方程可以得出该介质中的辐射场，也可称为时谐电磁源的推迟场，具体为：

由式（15）可得分量表达式：式中：

代入式（17），可得辐射磁场为：

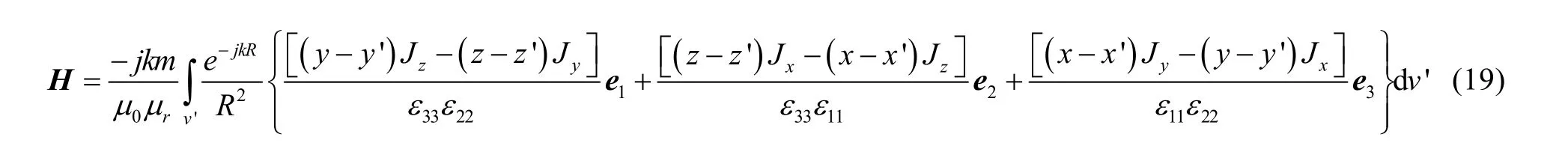
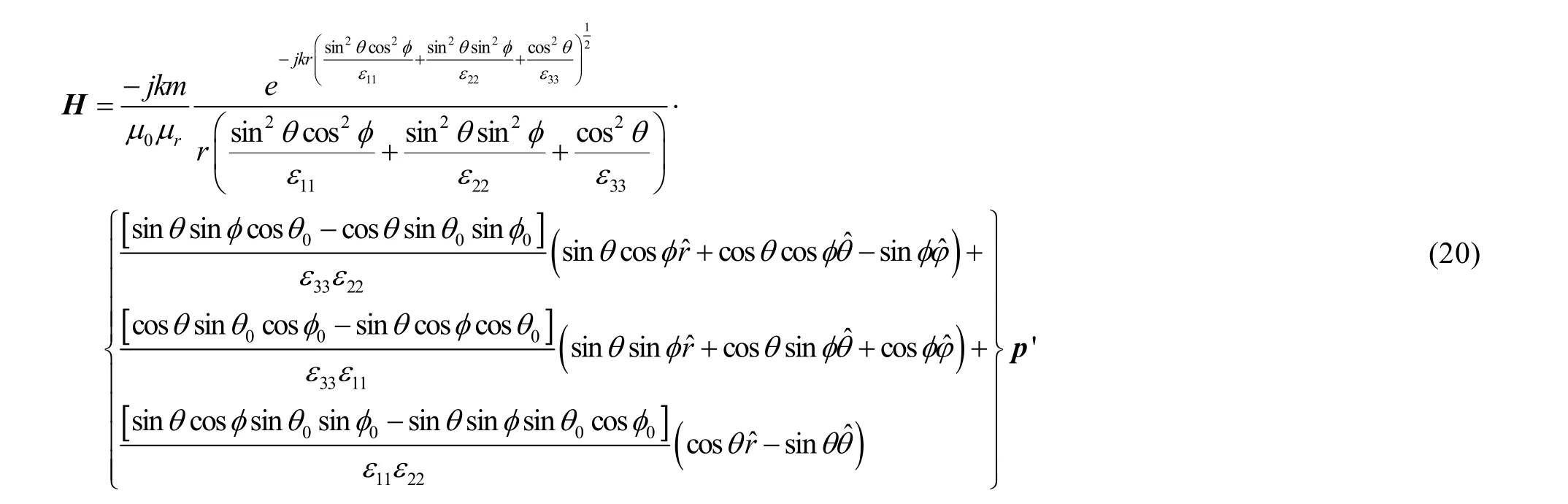
其中：

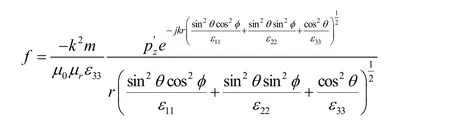
代入（17）可得：

式（21）、（22）是各向异性介质中电偶极子的辐射场。当介质为各向同性介质，即ε33=ε22=ε11=ε，式（21）、（22）变为：

其中m，k的具体表达式见式（19）。以典型各向异性介质石膏为例，观测点距电偶极的距离为10 km，其相对介电常数为εr=9.9e1e1+5.1e2e2+4.6e3e3。式（24）的部分仿真结果如图1—4所示，在垂直于电偶极的方向，辐射最强，这一点和各向同性介质中的电偶极辐射相同。当φ从0增加到0.5π的过程中，辐射不断增强。当观测点位于（0.5π，0），与电偶极子垂直方向的相对介电常数为5.1；当观测点位于（0.5π，0.5π），与电偶极子垂直方向的相对介电常数为9.9。由于在笛卡尔坐标系中三个坐标轴方向的介电常数具有相同的地位，因此图1表明，在各向异性介质中，电偶极的辐射特性具有各向异性特性。也就是说，在某一方向观测时，与该方向垂直方向的介电常数越大，辐射越强，反之亦然。图2为辐射随角度φ的变化，径向辐射的变化特点与图1相同。图3表明，在电偶极子方向上的介电常数越大，径向辐射越小，图4为介电常数张量对径向辐射的影响，可以看出，随着介电常数的增大，径向辐射增强，与图1具有相同的变化规律。各向异性介质中电偶极子辐射的各向异性特性为涂覆各向异性介质目标的识别与隐身设计提供了理论参考。

图1 能流密度随θ的变化

图2 能流密度随φ的变化

图3 能流密度随ε3的变化

图4 能流密度随ε1，ε2的变化

2 结语

基于电磁场的方向长度多标准理论，研究了各向异性介质中的光电辐射问题。首先提出了各向异性介质中的洛伦兹规范，得到了电各向异性介质中的d'Alembert方程。以此为基础获得了各向异性介质中时谐场的推迟势表达式，与各向同性介质空间的推迟势进行比较，验证了该表达式的正确性。以电偶极子为例，对各向异性介质中的辐射电磁场特性进行了仿真与分析，给出了各向异性介质中电偶极子辐射场的表达式。当介质为各向同性介质时，所得结果与现有文献结果完全一致，表明了结果的正确性。文中所得结果为各向异性介质如降雨、等离子体中的雷达、天线等工程设计以及各向异性介质天线、各向异性介质波导和各向异性目标检测等领域研究提供了理论基础和有益探索。

[1]ZHUCK N P,OMAR A S.Radiation and Low-Frequency Scattering of EM Waves in a General Anisotropic Homogeneous Medium[J].IEEE Transactions on Antennas and Propagation,1999,47(8):1864—1873.

[2]TAI C T.Dyadic Green’s Function in Electromagnetic Theory[M].2nd Edition.New York:IEEE Press,1994.

[3]WEIGLHOFER W S.Analytic Methods and Free-space Dyadic Green’s Function[J].Radio Science,1993,28(5): 847—857.

[4]PRZEZDZIECKI S,LAPRUS W.On the Representation of Electromagnetic Fields in Gyrotropic Media in Terms of Scalar Potential[J].J Math Phys,1982,23(9): 1708—1712.

[5]KAKLAMANI D I,UZUNOGLU N K.Radiation of Dipole in an Infinite Triaxial Anisotropic Medium[J]. Electromagn,1992,12(3):231—245.

[6]LAKHTAKIA A,WEIGLHOFER W S.Source-region Electromagnetic Field in an Affinely Transformable AUBM[J].International Journal of Infrared Millimeter Waves,1998,19(1):95—106.

[7]OLYSLAGER F,LINDELL I V.Closed form Dreen’s Dyadic for a Class of Bi-anisotropic Media with Axial bi-anisotropy[J].IEEE Transactions on Antennas& Propagation,1998,46(12):1888—1890.

[8]ZHUCK N P,OMAR A S.EM Wave Excitation and Propagation in a Generally Anisotropic Homogeneous Medium[J].IEEE Antennas and Propagation Soc Int Symp,Newport Beach,1995,CA,1(1):756—759.

[9]李瑾,各向异性介质中的库仑定律—多长度标准的应用[J].激光与电磁子学进展.2015,52(1):062601-1-062601-5.

[10]LI Y L,HUANG J Y.The Scales Transformation of Electromagnetic Theory and Its Application[J].Chinese Physics,2005,14(4):646—651.

[11]LI Y L,WANG M J,DONG Q F.Investigation of Electric Fields Inside and Outside a Magnetized Cold Plasma Sphere[J].Chinese Physics B,2010,19(11):115204-1-4.

[12]LI Y L,WANG M J.Electric Fields Inside and Outside an Anisotropic Dielectric Sphere[J],Chinese Physics B, 2009,18(6):2420—2425.

[13]LI Y L,LI J,DONG Q.F,et al.Internal and External Electric Fields for An Anisotropic Dielectric Particle in Electromagnetic Beams[J].IEEE Transaction on Antennas and Propagation,2013,61(9):4754—4758.

[14]LI Y L,LI J,DONG Q.F,et al.Investigation of Scattering for Uniformly Anisotropic Sphere[J].Acta Optica Sinica,2012,32(4):0429002-1.

[15]陈燊年.介质为各向异性的电磁场[M].北京:科学出版社,2012.

[16]WILLIAM H.HAYT.J,John A B.Engineering Electromagnetics[M].New York:Mc Graw Hill,2010.

Anisotropic Radiation Characteristics of Electric Dipole

LI Jin1,2,FENG Xiao-yi2,WANG Min g-jun3
(1.Department of Computer and Electronic Information,Shaanxi Xueqian Normal University,Xi′an 710100,China; 2.College of Electronic Information,Northwestern Polytechnical University,Xi′an 710072,China; 3.College of Electronic Information,Xianyang Normal University,Xianyang 712000,China)

ObjectiveTo study radiation property and radiation law of electromagnetic sources in homogeneous anisotropic medium.MethodsBased on the direction multi length standard theory of EM waves,the non-homogeneous differential equation of scalar potential was established.By solving this equation,explicit exact representations of scalar potential and magnetic vector potential were developed respectively;and their validity were demonstrated through comparing them with the available literatures.ResultsThe radiating field of an electric dipole was acquired in the presence of anisotropic medium,and this obtained radiating field was in agreement with that in the available reference as the material being the isotropic one.The radiation characteristics of the electric dipole were simulated and analyzed physically.ConclusionIn the anisotropic medium, the radiation of an electric dipole has the anisotropic property.When radiation is observed in one direction,the larger the dielectric constant in the direction vertical to the observing direction is,the more intensified the radiation is.It provides a theoretical basis for engineering optimization design of radar and antenna in anisotropic media such as magnetized plasma.

electromagnetic radiation;electric dipole;scales theory.

10.7643/issn.1672-9242.2017.07.004

TJ760.6+1；O451

A

1672-9242(2017)07-0018-06

2017-04-19；

2017-05-15

国家自然科学基金资助项目（60971079）；陕西省教育厅自然科学基金资助项目（16JK1185）

李瑾（1986—），女，硕士，主要研究方向为电磁波传播与散射。