基于四面体六棱长的三站测时差立体定位方法
宋文彬,乔文昇,马 霞
(中国电子科技集团公司第十研究所,成都 610036)
基于四面体六棱长的三站测时差立体定位方法
宋文彬,乔文昇,马 霞
(中国电子科技集团公司第十研究所,成都 610036)
针对在三站测时差立体定位中辐射源位置不能唯一确定的情形,提出一种简单易懂、计算方便、可操作性强的解析解方法,以解决求解双曲面方程组的繁琐问题。首先利用三站相互之间的距离、由量测时差值换算得到的两个距离差值,以及辐射源至主站的距离(设为变量r)总共6个参数,立足于已知6条边长判断能否构成四面体的理论,求得r的取值范围;然后在r的值域范围内任意给定某个具体值,加上已知三站的地理位置,通过解三元一次方程组的形式获得目标在三站所在平面内垂直投影的坐标(设为变量Xh),并计算出目标至垂直投影的距离(设为变量h);最后由Xh和h给出目标在地心地固直角坐标系下的坐标。
三站,无源定位,TDOA,解析几何
0 引言
无源定位中的多站到达时差(Time Difference of Arrival,简称TDOA)定位技术因不需要全局时间同步,而且定位精度高、实时性好,在传感网络定位系统中得到了广泛应用。在TDOA定位中,一个时差估计值对应的是以两个传感器节点为焦点的一对双曲面,多个时差估计值对应多条双曲面,这些双曲面的交点即为被测信号源的位置。一般情况下,求解双曲面方程组非常繁琐,不容易得到方程的解析解,而且会出现多值现象,需要进行解模糊处理[1-2]。有时为了简化计算,假定传感器与信号源位于同一平面内,利用平面内的双曲线进行相交求解[2]。目前TDOA定位主要采用约束线性最小二乘算法,典型的如Chan等[3]提出的二次纠正最小二乘法,Huang等[4]基于拉格朗日乘子法提出的线性纠正最小二乘法以及Yang等[5]提出的基于牛顿迭代法的约束总体最小二乘法等。另外还有其他一些基于迭代[6]、统计[7]或者滤波[8-9]等手段的求解方法。本文针对三站TDOA立体定位问题,绕开复杂的双曲面方程组求解过程,采用立体解析几何的方法直接给出满足两量测时差条件的信号源所有可能位置的解空间。
1 三站测时差立体定位方法
1.1 三站测时差定位问题
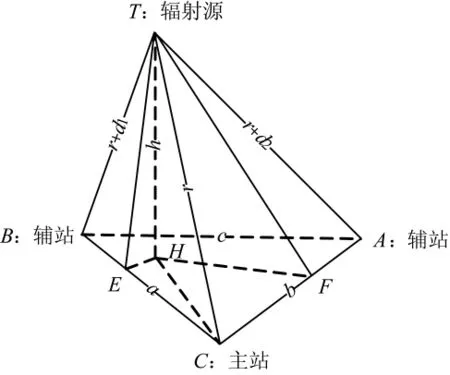
图1 三站测时差立体定位示意图
如图1所示,设空间有A、B、C三站,其中C为主站,A、B为辅站。三站测时差定位系统同时测量辐射源T的辐射到达主站C与辅站B之间的时间差△t1、到达主站C与辅站A之间的时间差△t2。假定T至C的距离为r,则T至B、A的距离分别为r+d1和 r+d2,其中 d1=c△t1,d2=c△t2,c 为光速。因为只有3个站,无法唯一确定辐射源T的位置,一般做法是认为台站与辐射源均在同一水平面内,利用两条双曲线相交得到辐射源的位置。然而在工程应用中,大部分情况是3个台站位于地面,高度往往不同,而且辐射源位于空中,如果采用二维解算的方法,将会带来不小的定位误差。如果直接在立体空间求解,两条双曲线就变作两个双曲面,相关的方程组如下。
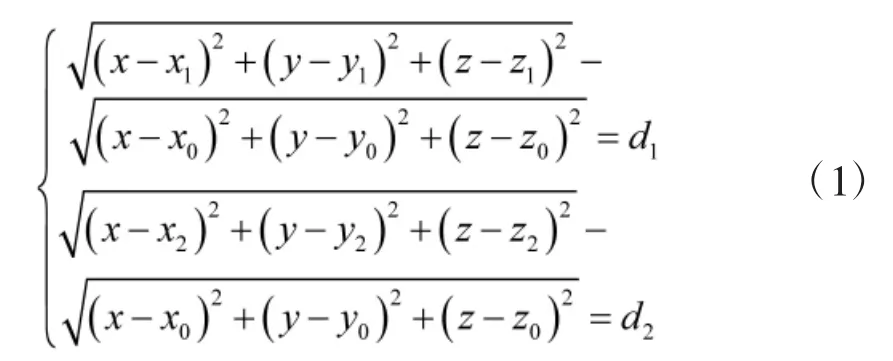
其中(xi,yi,zi),i=0,1,2是主站与两辅站的坐标,以解析解的形式讨论式(1)存在实根的情况是极其繁杂的。
1.2 三站测时差立体定位算法原理
如图1所示,三站之间的距离分别令作a,b,c,加上辐射源T至它们的距离r,r+d1,r+d2,一共6个正数,其中r为未知数。如果辐射源存在的话,即空间存在4个点,它们之间的直线距离等于以上6个正数。针对该问题,参照2008年曾中君证明的六正数构成四面体六棱长的充要条件[10],增加4个点在同一个平面的情形,只须将曾中君推导的不等式由“〉”改为“≥”,具体如下。

即如果变量 r使得式(2)成立,且使得 r,r+d1,r+d2均为正数,则按照曾中君证明的充要条件可得出,a,b,c,r,r+d1,r+d26 个正数能够构成一个四面体的六棱长,四面体的4个顶点分别为3个基站的位置和满足时差条件的辐射源T的位置;反之如果变量 r不能同时使得不等式(2)和 r,r+d1,r+d2均为正数成立,则 a,b,c,r,r+d1,r+d26 个数将不能够构成一个四面体的六棱长,也就不存在满足时差条件的辐射源T。
将式(2)化简可得:
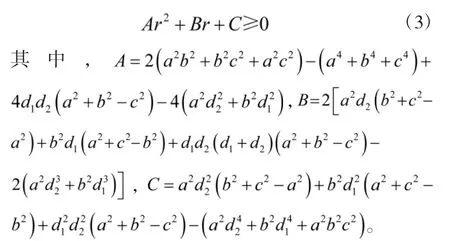
1.3 三站测时差立体定位算法步骤
三站测时差立体定位方法包含以下4个具体步骤:
1.3.1 计算基线长度
设主站C和辅站B、A的经纬高分别为li,mi,hi,i=0,1,2,利用式(4)、式(5)计算基线长度 a,b,c。先利用式(4)计算三站在地心地固(ECEF)直角坐标系下的坐标值 xi,yi,zi。

其中子午圈第一偏心率平方e2=0.00669438,椭球卯酉圈曲率半径,赤道半径R=6378 137m。再利用式(5)计算出它们之间的直线距离。

1.3.2 计算满足不等式条件的r的取值范围
首先保证辐射源T至三站的距离均为正数,有约束条件 r〉max(0,-d1,-d2),其中 max表示取最大值。
接着讨论式(3)对 r的约束作用,定义△=B2-4AC,有以下7种情况:
②当A〉0,△≤0时:对r的取值没有进一步约束;

④当A<0,△<0时:不存在符合条件的r值;
⑦当A=B=0时:若C≥0,则对r的取值没有进一步约束;若C<0,则不存在符合条件的r值。
1.3.3 计算辐射源T在三站所在平面内投影的坐标
在计算出的取值范围内任意给定某个r值,利用3个线性式(6)~式(8)解出辐射源(如图1中H点所示)。在3个观测站所在平面内垂直投影的坐标 xH,yH,zH。
线性方程之一是式(6),它代表三站所在的平面(见图1中ΔABC):

线性方程之二是式(7),它代表以主站C为圆心、r为半径的球面与以辅站B为圆心、r+d1为半径的球面相交所确定的环所在的平面(见图1中ΔTEH,点E为点H在直线BC上的垂足):

线性方程之三是式(8),它代表以主站C为圆心、r为半径的球面与以辅站A为圆心、r+d2为半径的球面相交所确定的环所在的平面(见图1中ΔTFH,点F为点H在直线AC上的垂足):

1.3.4 计算辐射源T的坐标
首先定义参数p,q,s,其含义是直线TH的方向数,大小分别为:
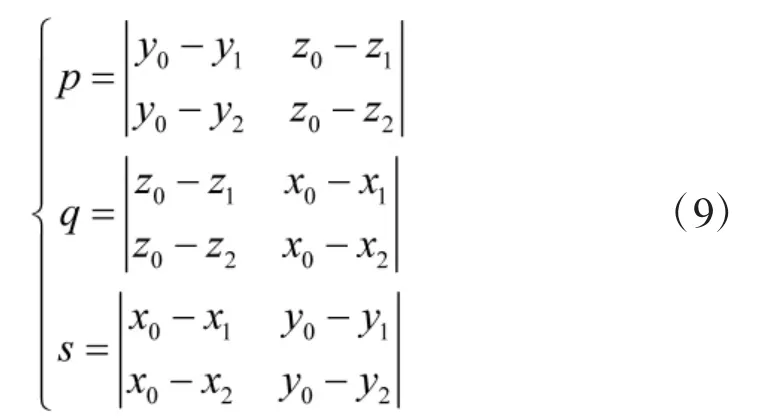
再计算线段TH的长度h:

最后辐射源T在ECEF直角坐标系下的坐标xT,yT,zT为:

再利用坐标变换公式将xT,yT,zT转成经纬高,通过高度信息进一步定出目标位置或范围。
2 仿真分析
设A、B、C三站的地理位置及测得的两个时差的值如下页表1所列,经计算得三站之间的距离分别为:a=18 332.8,b=20 372.5,c=362 78.1(单位:m),辐射源至观测站的距离差分别为:d1=-11 700,d2=1 800(单位:m,这里令光速为 3×108m/s)。
如果采用求解双曲面方程组的方法,方程组形式见式(1),其中(xi,yi,zi)(i=0,1,2)的值可由三站的经纬高经坐标变换至ECEF坐标系得出。化简需要经过两次平方才能完全去除开方操作,因此,需要讨论因平方引入增根的问题。化简后剩下的就是求解三元二次方程组了,在求解的过程中,也涉及到可能存在无解的情形。与本文提出的仅需求解三元一次方程组和无需讨论增根的方法相比,显然要复杂得多。下面详细介绍如何使用本文提出的方法求解上述仿真实例。

表1 仿真场景参数设置
将上述5个参数代入式(3)得到:

以及△=8.883×1043m10。可见它属于1.3.2节中的第①种情形,得到r的取值范围为:r≥158315.0m。

图2 目标可能位置的经纬度
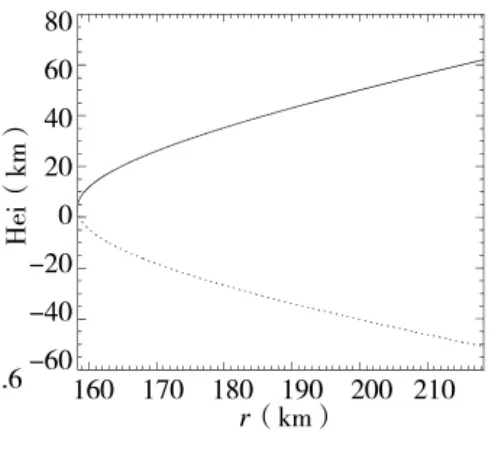
图3 目标可能位置的高度
本文取满足条件的r值(158 315≤r≤218 315),利用上节中的算法,计算目标可能的位置,结果如图 2、图 3所示,其中实线是式(11)中取“+”号的结果,虚线是取“-”号的结果。现假设经辐射源识别目标为面目标,高度范围为0 m~1 000 m,则它属于虚线段范围,计算得目标的经纬度范围分别为[121.115 44,121.116 67]与[31.053 97,31.055 07],在水平面的分布范围约为170 m;若目标为空目标,高度范围为5 000 m~15 000 m,则它属于实线段范围,计算得目标的经纬度范围分别为[121.113 92,121.133 25]与[31.052 3,31.066 62],在水平面的分布范围约为2 452 m。如果是采用二维定位方法,则只能求出水平面内的某一个或两个点,而忽略了很多其他可能的解。
3 结论
本文利用已知六边长能否构成四面体这个充要条件,仅用辐射源至主站距离这一个参数,解出了辐射源存在解的边界条件。每一个符合要求的值,均对应了1~2个辐射源可能的位置。相比于常用的二维求解方法,解的空间极大地拓展了,而且合理利用了三站的高度信息;相比于联立双曲面方程组及其数值求解的方法,这里只要求解三元一次方程组,大大地节省了繁琐的双曲面方程组求解过程和解模糊的处理,具有良好的工程应用前景。在实际应用时,利用双时差求得目标所有可能位置后,通过进一步研判它可能在的大致高度,即可得出目标更加准确的地理位置。
[1]俞志强,叶朝谋.四站三维时差定位模糊分析[J].空军雷达学院学报,2009,23(5):370-372.
[2]韩丽君.平面三站时差定位中的模糊研究[J].计算机与数字工程,2012,40(5):10-11.
[3]CHAN Y T,HO K C.A simple and efficient estimator for hyperbolic location [J].IEEE Trans.on Signal Processing,1994,42(8):1905-1915.
[4]HUANG Y,ELKO G W,MERSEREAURM.Real time passive source localization:a practical linear correction least squares approach [J].IEEE Transactions on Speech and Audio Processing,2001,9(8):943-956.
[5]YANG K,AN J P,BU X Y,et al.Constrained total least squares location algorithm using time difference of arrival measurements [J].IEEE Transactions on Vehicular Technology,2010,59(3):1558-1562.
[6]史洪宇,贺前华,魏晓慧.基于遗传-拟牛顿混合算法的到 达 时 间 差 定 位 [J].计 算 机 工 程 ,2011,37(11):220-222.
[7]刘影,钱志鸿,王雪,等.基于到达时间差的无线传感器网络质心定位算法 [J].吉林大学学报,2010,40(1):245-249.
[8]陈曦,彭华峰,同武勤.基于卡尔曼滤波的三星时差运动目标定位技术[J].电讯技术,2011,51(5):77-81.
[9]赵侃,谢恺,漆德宁.基于多时刻时差的三星时差定位跟踪算法[J].航天电子对抗,2012,28(2):24-25.
[10]曾中君.六正数构成四面体六棱长的充要条件[J].数学教学通讯,2008,76(12):38-39.
An Algorithm of Tri-station 3D TDOA Positioning Based on Six Side-length Values of a Tetrahedron
SONG Wen-bin,QIAO Wen-sheng,MA Xia
(No.10 Research Institute,China Electronics Technology Group Corporation,Chengdu 610036,China)
Aimed at the ambiguity occurring in the passive tri-station 3D TDOA positioning system,a simple,lowly-computational and highly-operable algorithm is proposed to resolve the hyperbolic location equations.Firstly,using six parameters which includes the distances between every two stations,the distance differences obtain from two measured time differences,and the distance between the radiation source and the main station(let it be r),simultaneously based on the theory of judging whether six positive number be able to construct the lengths of a tetrahedron’s six sides,the permissive value range of r is gotten.Secondly,for any value of r in the permissive range,the detailed positions of three stations is given,the coordinate of the target’s vertical projection (let it be Xh)in the plane of three stations can be calculated by resolving three-variable linear equations.Moreover,the distance between the target and the projection (let it be h)can be also calculated.Lastly,the target’s earth-center and earth-fixed(ECEF)coordinate is analytically expressed by the parameters of Xhand h.
tri-station,passive location,TDOA,analytic geometry
TN957.52
:A
10.3969/j.issn.1002-0640.2017.06.034
2016-05-05
:2016-06-07
宋文彬(1981- ),男,江西九江人,博士,高级工程师。研究方向:目标跟踪、目标识别与图像处理。
1002-0640(2017)06-0150-04
——三角形一个共线点命题的空间移植

