导弹武器系统研制费用估算方法
卞立新,罗兴柏,李金明,张 伟
(1.军械工程学院,石家庄 050003;2.中部战区陆军66285部队,河北 怀来 075411)
导弹武器系统研制费用估算方法
卞立新1,罗兴柏1,李金明1,张 伟2
(1.军械工程学院,石家庄 050003;2.中部战区陆军66285部队,河北 怀来 075411)
针对导弹武器系统研制费用相关数据样本量少,变量之间存在严重共线性等问题,提出了一种基于偏最小二乘法的研制费用估算模型。引入库克距离对原始数据进行识别,并剔除异常数据,采用灰色关联度分析法选取相关度高的自变量,提高模型准确性和稳定性。利用偏最小二乘法进行数据拟合,估算出导弹武器系统的研制费用。应用算例的计算结果表明,该方法建立的研制费用估算模型拟合度良好,计算误差在8%以内。
研制费用,导弹武器系统,偏最小二乘法
0 引言
导弹武器系统的费用估算是武器装备发展过程中的重要决策活动,为了保证资源的有效利用,需要在导弹武器系统研究初期进行费用估算,以降低研制费用和风险。有关资料显示研制阶段费用占全寿命周期费用的10%~15%[1],但却影响武器系统全寿命周期费用的95%。说明武器系统研制阶段的费用投入直接影响后续费用的多少,需要充分重视。
目前研制费用的预测采用较多的是基于BP神经网络[2]和工程估算法[3]。此外,遗传算法[4]、灰色组合模型[5]和最小二乘回归法[6]也被应用于导弹武器系统研制费用估算中。各类方法存在着各自的缺陷和不适用范围,例如:BP神经网络容易陷入局部最优解;工程估算法只适用于后期设计细节清晰时的费用估算;传统的灰色组合模型法会带来较大的估计误差;最小二乘回归法适用于数据样本量大的情况。
大多数研制费用估算模型在建立时,直接使用原始数据,影响了模型准确性。为解决这一问题,本文选用库克距离识别出异常数据,采用灰色关联度分析法,减少自变量的个数,在此基础上利用偏最小二乘回归方法建立研制费用参数模型。
1 原始数据的处理
原始数据的真实、有效是保证所建立的装备费用模型准确的关键,因此,在建模之前必须对所收集到的数据进行相应的处理。
1.1 数据的诊断与识别
原始数据中存在的异常值会影响到所建立模型的准确性,因此,在利用原始数据建立模型前必须对数据进行诊断和筛选,找出异常值,并确定是保留还是剔除。
本文采用库克距离法[7]来进行判断。库克距离可有效降低共线性问题对判断异常数据的影响。第i组数据对回归方程参数的影响程度用库克距离Di表示,Di等价形式可以表达为:

式中,hii为杠杆值,ri为学生化残差,p为自变量个数。
从式(1)中可以看出,Di是学生化残差的平方与杠杆值的一个单调增函数的乘积,Di越大,表明在删除第i组数据之后,回归方程参数的改变程度也就越大。若Di值较其他组明显偏大,则认为对回归方程存在影响,应当剔除该组数据[8]。
1.2 多重共线性诊断
多重共线性是指在变量之间存在着线性相关的现象,会导致结果存在极大的偏差,或是很不稳定。方差膨胀因子VIF是用来衡量一组变量的共线性程度的统计量。
自变量xj的方差膨胀因子记为(VIF)j,计算方法为:

所有变量中的最大(VIF)j被用来作为测量多重相关性的指标。一般认为如果最大(VIF)j超过10,通常表示多重相关性严重[9]。
1.3 自变量的选择
自变量的选择是导弹武器系统费用模型建立中的一个关键步骤,选择的变量要尽可能不遗漏重要的解释因素,使模型具有说服力,同时变量的个数要尽可能少,降低模型的复杂度。本文采用灰色关联度分析法来选择自变量,灰色关联度分析法是根据序列曲线之间的相似程度来判断其联系是否紧密。曲线越相似,相应序列之间的关联度也就越大,反之越小[10]。
灰色关联度分析数据之前,需要对原始数据进行无量纲化处理,本文采用标准化处理方法对原始数据进行处理,即对变量xi,经过无量纲化处理后x'为:

参考曲线xi与曲线xi(i=1,2,3,…,n)在k点的关联系数可表示为:
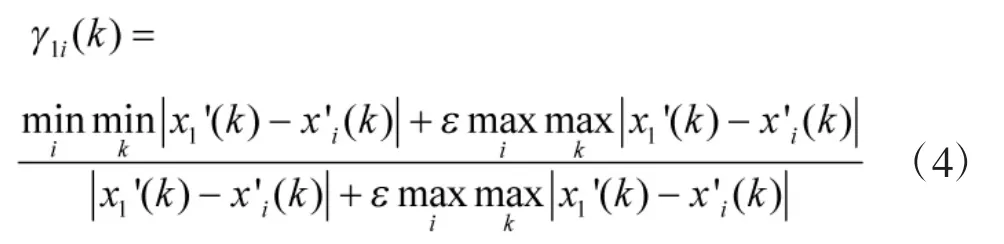
曲线xi与参考曲线x1的关联度可表示为:

γ1i越大,表明曲线xi与参考曲线x1的关联度越大。利用关联度分析可得到费用与各特征参数之间的关联系数,一般将γ1i〉0.6视为选取的标准,以此为基础选择自变量来建立费用参数模型。
2 研制费用参数模型
2.1 偏最小二乘法的基本原理
设因变量 y∈Rn,自变量集合为 X=[x1,…,xp],建立y对x1,…,xp的回归模型,为方便起见,先将数据作标准化处理,记 E0=[E01,…,E0p]n×p是 X 经标准化后的数据矩阵,F0=(F01,…,F0n)是因变量 Y 的标准化变量[9],分别在E0和F0中提取出成分t1和u1,分别实施E0对t1的回归以及E0中对u1的回归,如果满足精度要求,则终止计算,否则,利用E0被t1解释后的残余信息和F0被u1解释后的残余信息,进行下一步的成分提取,重复此过程直到达到满意精度为止。若最终得到的m个主成分t1,…,tm,可得到F0关于t的回归模型,最后转化成y对x1,…,xp的回归方程表达式。
2.2 建模步骤
①已知数据E0、F0,从E0中提取第1个成分t1。t1=E0*w1,其中w1是E0的第1个轴,是一个单位向量,且w1是对应矩阵E0TF0F0TE0T最大特征值的单位特征向量。从F0中提取第一个成分u1,u1=F0c1,且‖c1‖=1,由于 F0是一个变量,因此,u1=F0。
②分别求出E0,F0在t1上的回归方程,可得:

③检验交叉有效性,若Qh2≥0.097 5则重复第2步计算,直到交叉有效性条件,否则,只提取一个成分t1,停止计算。
④可确定偏最小二乘回归中成分t提取的个数m。利用得到的m个主成分t1,…,tm,即可得到F0关于t的回归模型,得:

式中,FA为残差矩阵。
⑤由于t1,…,tm都是E0的线性组合。因此,F0可写成E0的线性组合,即:

⑥最后可将式(8)还可以转化成y对x1,…,xp的回归方程表达式,即:
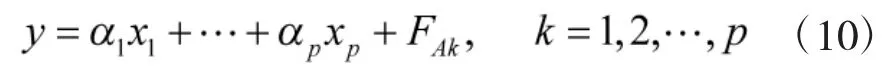
式中,FAk是残差矩阵FA的第k列。
下面给出交叉有效性的定义:
记 yi是原始数据,t1,…,tm为主成分,yˆhi是使用全部样本点,拟合含有t1,…,tm主成分的回归方程中第 i个样本的预测值,yˆh(-i)是删除样本点 i,并代入前面拟合方程,得到样本点i上的拟合值。计算Qh2方法如下:
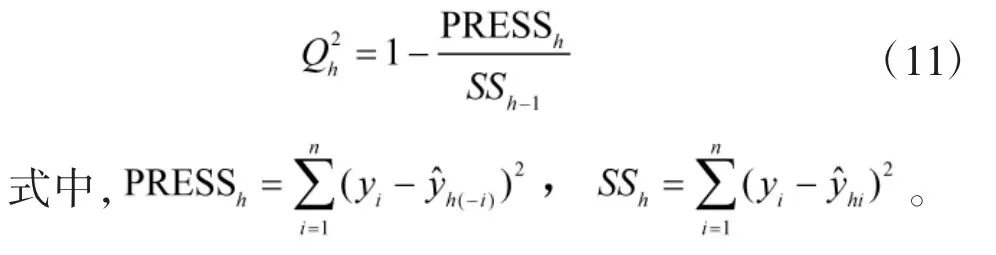
3 实例计算
本文以估算某型导弹研制费用为例,其研制费用和相关性能参数数据如表1[11]所示。
3.1 实验数据处理
对原始数据进行异常值检验,检验是否存在异常值,结合考虑杠杆值hii、学生化残差ri和库克距离Di。利用SPSS软件对原始数据计算处理可得到各项指标值如表2所示。
通过表2可以看出,第6组数据的Di高达6.843,而其余组数据的Di都非常小,因此,应删除第6组数据。通过残差ei可以看出通过传统最小二乘法拟合的结果有较大的误差。
删除第6组数据后,利用式(2)可计算出方差膨胀因子如表3所示。
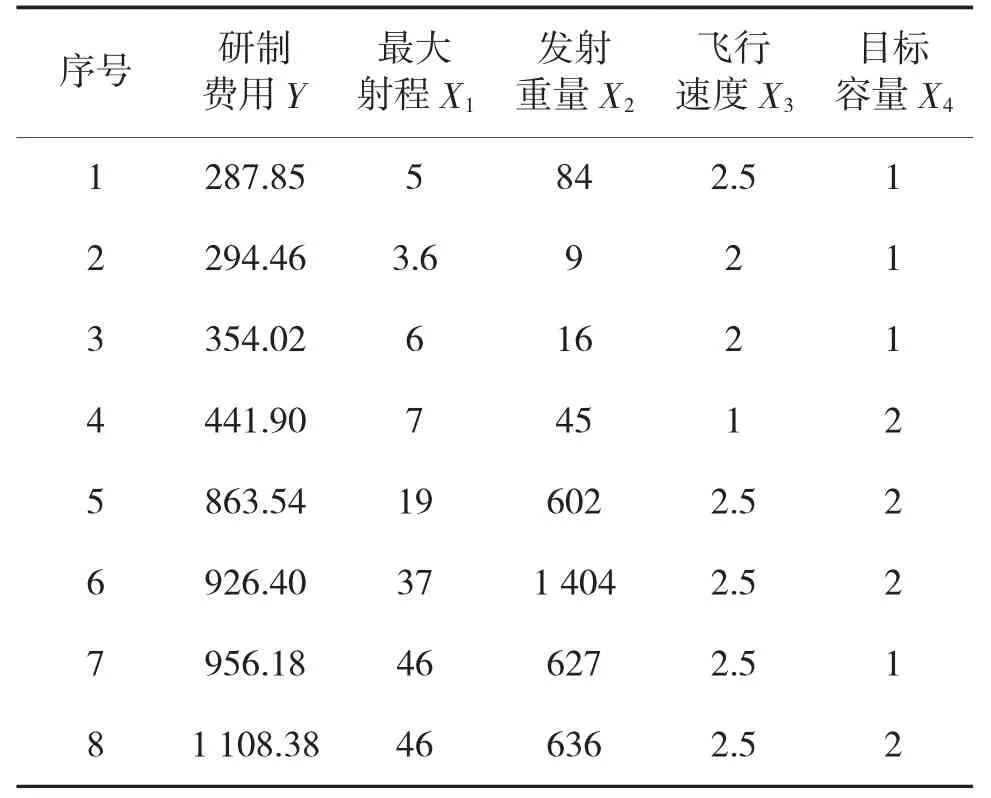
表1 导弹研制费用与性能参数原始数据表

表2 异常值检测结果

表3 方差膨胀因子
从表3可以看出最大的方差膨胀因子(VIF)2=15.627〉10,说明了自变量之间存在多重共线性。
3.2 变量的选择
原始数据经过无量纲处理后利用式(3)、式(4)可得到各个变量的关联度系数分别为:γ12=0.846 1,γ13=0.815 4,γ14=0.562 2,γ15=0.792 6。
由关联系数可知发射重量与研制费用的关联度最大,最大有效射程关联度次之,然后是目标容量的关联度,飞行速度的关联度最小。由于飞行速度的关联度γ14<0.6,因此,只选择前3个自变量。
3.3 参数费用模型的建立
选择前3个自变量后,将其原始数据经过标准化处理后的数据如表4所示。

表4 3个自变量的标准数据表
通过输入数据,运行偏最小二乘的建模程序,得到各成分的交叉有效性分别为Q12=0.973,Q22=0.073。按Qh2≥0.097 5的决策标准,只提取一个成分,即取第一个成分t1来拟合方程。
最后得到标准的偏最小二乘回归方程为:

经换算得到原始数据偏最小二乘回归方程为:

利用SIMCA-P软件对数据进行分析得到变量投影重要性指标如图1所示,该指标用来描述相应的自变量对因变量解释能力的大小,目的是以量化的方式说明各因素(VIP)i对因变量影响的大小。

图1 投影重要性指标
从图1中可以看出,各自变量的(VIP)i均大于0.6,说明自变量可以解释因变量,并且可以看出发射重量的解释能力最大,射程次之,目标容量最小,这与前面灰色关联度分析结果是相同的,也间接证明了灰色关联度分析法的有效性。
费用估算结果如表5所示。

表5 费用估计值
导弹武器系统的总研制费用和总研制费用估计值的比较如图2所示。
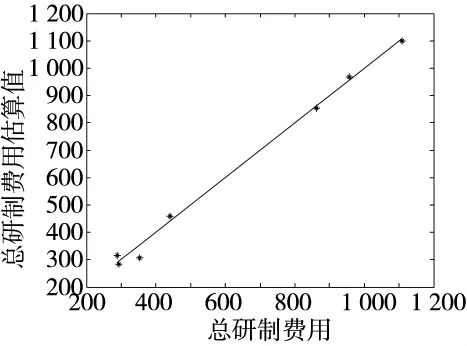
图2 预测值与观测值比较
由图2可看出,总研制费用与总研制费用估计值的误差很小,说明所做的费用参数模型对武器装备费用的预测是满意的,同时亦可看出,随着费用的增大,预测的结果越来越准。
4 结论
本文采用库克距离对原始数据进行识别处理,确保建模所需数据的有效性,并采用偏最小二乘法建立了导弹武器系统研制费用估算模型。通过实例计算可得到如下结论:
①基于偏最小二乘法建立的研制费用估算模型处理数据样本量少,且变量间存在共线性问题方面具有独特的优势;
②与传统方法相比本文建立的模型精度较高,计算误差在8%以内。
③本方法是装备早期研发费用估算的一种方法,而对全寿命周期的费用估计需要综合采用不同种类的方法进行分析估计,对于其他阶段的装备费用估计有待进一步研究。
[1]李明,刘澎.武器装备发展系统论证方法与应用[M].北京:国防工业出版社,2000.
[2]尤高升,陈文俊,郝中军.基于BP神经网络的导弹系统研制费用预测[J].科技信息,2010,27(32):107-108.
[3]THOKALA P,SCANLAN J,CHIPPERFIELD A.Life cycle cost modelling as an aircraft design support tool[J].Aerospace Engineering,2009(3):224-229.
[4] CURRAN R,CASTAGNE S,EARLY,et al.Aircraft cost modelling using the genetic causal technique within a systems engineering approach [J].The Aeronautical Journal,2007(11):532-536.
[5]杨梅英,沈梅子.基于灰色组合模型的发动机研制费用估算研究[J].数学的实践与认识,2006,36(10):162-166.
[6]DOE G 430.1-1.Cost estimating guide,U.S.[S].New York:Department of Energy,1997.
[7]FIENBERG S E.The analysis of classified categorical data[J].Trans.Ser.Edinburg,2010(3):156-164.
[8]王寅琮.回归分析中异常值与共线性的诊断[D].秦皇岛:燕山大学,2012:34-37.
[9]王惠文.偏最小二乘回归方法及其应用[M].北京:国防工业出版社,1999.
[10]刘思峰,谢乃明.灰色系统理论及其应用[M].北京:科学出版社,2013.
[11]赵英俊,刘铭.武器型号费用参数模型的数据诊断与识别[J].上海航天,2000,17(2):43-45.
Method of Development Cost Forecasting for Missile Weapon System
BIAN Li-xin1,LUO Xing-bai1,LI Jin-ming1,ZHANG Wei2
(1.Ordnance Engineering College,Shijiazhuang 050003,China;2.Central Theater Command of 66285,Huailai 075411,China)
Due to the mall samples size,and multicollinearity relationship of variables of the missile weapon system development cost.the missile cost estimation model is established based on the partial least regression.Cook distance is used to recognition of abnormal data,and the grey relation grade theory is used to elect independent variable that has highly degree of correlation for improve the accuracy and stability of model.Finally the partial least regression is used to fitting data for estimate development cost of missile weapon system.The results show that the model fit is fairly good,and the fit error is less than 8%.
development cost,missile armament system,partial least regression
E911;TJ76
:A
10.3969/j.issn.1002-0640.2017.06.031
2016-05-10
:2016-06-26
卞立新(1991- ),男,辽宁本溪人,硕士研究生。研究方向:弹药系统设计与试验评估。
1002-0640(2017)06-0136-04

