地球模型对横坐标惯导极区导航影响的分析
郝勇帅周爱军王海波
(1.海军大连舰艇学院研究生管理大队大连116018)(2.海军大连舰艇学院航海系大连116018)
地球模型对横坐标惯导极区导航影响的分析
郝勇帅1周爱军2王海波2
(1.海军大连舰艇学院研究生管理大队大连116018)(2.海军大连舰艇学院航海系大连116018)
以真北为航向基准的惯导算法在极区由于经线的收敛而失效,传统惯性导航系统难以完成极区导航的任务,利用地球横坐标系可以完成极区惯性导航的任务,论文对因地球模型的选取对横向坐标系极区惯导系统造成的影响进行了一些思考分析。
横坐标系;地球模型;横向经纬度
Class NumberTN96
1 引言
惯性导航系统作为一种完全自主式的导航系统,不向外界发出任何信号,完全依靠自身设备完成导航任务,隐蔽性好,受外界环境干扰小,在常年被冰雪覆盖的北冰洋,惯性导航系统是潜艇可以依赖的唯一导航设备。由于我国地理位置的限制和对极区探索需求的不足,历史上对极区导航的研究较少。传统的惯性导航系统通常采用指北方位机械编排,在该机械编排下,选取当地地理坐标系为其导航坐标系,以经线为航向基准。在极地地区,由于经线收敛于极点,当载体通过极点附近时,真北方向的变化速率趋向于无穷大,从而导致计算溢出。在极点处,由于真北方向失去意义,更面临无航向基准的局面。为解决这一问题,可以将极点人为的转移至赤道,将地球坐标系横置,以横向经线作为极区导航的航向基准,此时地球模型的选取将会对系统误差产生影响。
2 横向坐标系
在传统的惯性导航系统中,地球坐标系与地球固连在一起,其坐标原点Oe为地心,ze轴与地轴重合,xe轴在赤道平面内,指向格林威治经线,ye轴也在赤道平面内,指向东经90°经线,三条坐标轴构成右手系。传统指北机械编排中,地理坐标系的原点Ot即为载体重心,zt轴与当地垂线重合,向上指向天向,xt轴和yt轴位于当地水平面内,xt轴沿经线指向北,yt轴与xt轴垂直指向东,三轴也构成右手系。
横向坐标系包括横向地球坐标系和横向地理坐标系。横向地球坐标系与地球固连在一起,原点为地心。选取东经90°经线与赤道的交点为横向北极点,横向地球坐标系的轴指向横向北极点,横向地轴为地心与横向北极点的连线。横向赤道平面为传统地球坐标系中本初子午面。轴和-轴在横向赤道平面内,轴指向真北极点,轴与轴垂直,三轴构成右手系。横向地球坐标系也可由地球坐标系Oexeyeze经过绕xe轴和ze轴的两次顺时针旋转得到。横向地球坐标系的-轴与地球坐标系的ze轴重合,轴与xe轴重合,轴与ye轴重合。横向地理坐标系的定义与地球模型的选取有关,并根据横向东向和横向北向定义的不同而不同。
3 地球模型对横向坐标系的影响
3.1 第一级近似
在地球圆球体模型下,垂直于横向地轴的平面交地球表面所得的曲线为横向纬线圈。过横向地轴的平面交地球表面所得的曲线为横向子午线圈。过真北极点的横向子午线圈为横向本初子午线圈。
如图1所示,在圆球体模型下,横向地理坐标系的天向即-zt轴方向沿当地垂线方向向上,横向地理坐标系的北向即-yt轴方向沿横向子午面与当地水平面的交线指向横向北极点,横向地理坐标系的东向即-xt轴方向沿横向纬线圈平面与当地水平面的交线方向指向东,三轴构成右手系。
但用圆球体模型作为惯性导航的地球参考模型存在原理性误差。观测和理论都表明,地球在事实上更接近于椭球体,其赤道半径比极半径约长21km,极扁率约为1/300。若在全球范围内采取圆球体模型无疑误差是很大的,所以只在高纬度地区导航时采用圆球体模型。
在载体由低纬度进入高纬度时,需要对导航模式进行切换。我们选取切换位置载体航向上的曲率半径为圆球体的半径。
如图2所示,椭球面与圆球面相切于P点,沿航行方向的法截线为PQ,设此段法截线长度为S。圆球体半径为KP即P点航行方向的曲率半径RΑ,圆弧ΡΡ1的圆心角为θ,弧长为S1。则S1可以表示成法截线长度S的函数,略去高阶项之后,与法截线长度相减,可以得到相应的圆弧和法截线长度的差值与法截线长度的关系,通过计算可得在子午圈方向上该差值最大,在1000km的距离上,法截线和相应的圆弧的长度误差在10m的量级上,可以忽略不计。同样,可以将KQ的长度表示为S和RΑ的函数的形式,再将其与RΑ相减,则可以得到圆球体模型和椭球体模型的高度差与法截线距离的关系,制成表格如下。
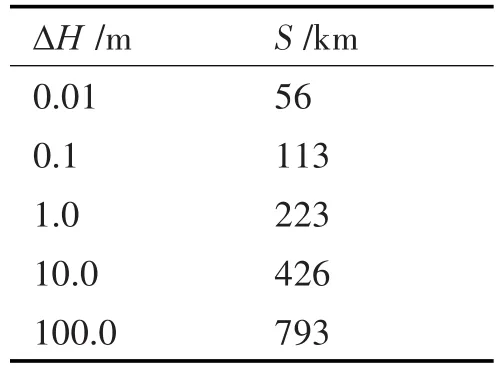
表1 圆球模型高度误差
由于惯导系统的高度通道是发散的,其高度误差会随时间迅速增加,如果在初始时刻存在1m的误差,则经过两个小时之后误差将会达到150km,这一误差水平是不可容忍的,因此,需要对其进行阻尼,或通过引入外部信息获得高度值。
圆球体模型不仅会带来高度上的误差,更重要的是会导致当地垂线的角度误差,垂线与当地实际地理垂线之间的偏差则会带来平台倾斜角的误差。显然,沿子午线方向航行带来的平台倾斜角的误差是最大的。
设载体沿子午线航行,以载体所在点的子午圈曲率半径为圆球体的半径,通过大地问题的反解,可以得到载体航行不同距离之后的真实纬度变化量,同时,可以得到经过该距离之后,在圆球体模型下的纬度变化量,两者相减,即为北向上由于地球模型导致的平台倾角误差ψ,制成表格为如表1。
表2表示在不同的纬度上,航行过一个纬度对应的距离所引起的平台倾角误差的值。由该表可以看出,转换纬度越高,航行一个纬度引起的误差角越小,因此在使用圆球体模型时应尽量在高纬度区域。若以80°为起点,则经过不同的距离引起的平台误差角如表3。
由表3可以看出,在350公里的范围内,地球模型带来的平台倾角误差就可以达到秒的量级,若加速度计零偏为100μg,则其与惯导系统的初始对准误差处于同一量级,与舒拉震荡引起的平台倾角误差的振幅也处于同一量级,所以应引起足够的重视。地球模型误差对系统误差的贡献还需对其进行仿真验证和误差分析。
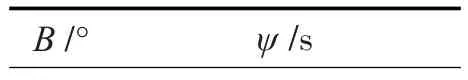
表2 倾角误差随纬度变化关系
0.2852 0.2104 0.1100 0.0539 0.0077
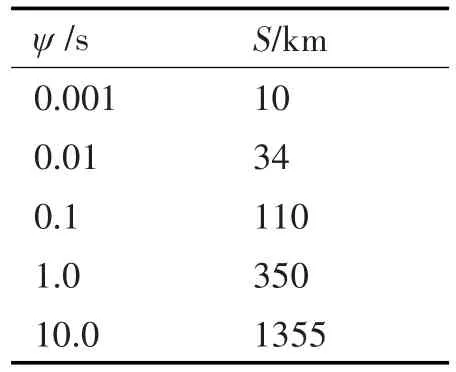
表3 倾角误差随距离变化关系
3.2 第二级近似
采用椭球体模型可以降低由地球模型引起的原理性误差,但在椭球体模型上的横向经纬度的定义值得讨论。
以上两图为两种不同的椭球体模型下的横向经纬度的定义。
第一种仿照传统经纬度来定义横向经纬度。如图3所示,过横向地轴-Ze的平面交地球表面所得曲线为横向子午线圈,过真北极点的横向子午线圈为横向本初子午线圈。垂直于横向地轴的平面交地球表面所得的曲线为横向纬线圈。Ot的横向经度为横向本初子午面与载体所处横向子午面之间的二面角λ1。Ot的横向纬度为地心垂线OtOe与横向赤道平面的夹角φ1,即用地心纬度代替地理纬度,横向地理坐标系的天向即-zt轴方向沿当地的地心垂线OeOt方向向上[5]。
第二种以地理垂线与各面之间的夹角来定义横向经纬度。如图4所示,Ot的横向纬度为ΚOt与横向赤道平面的夹角φ2,Ot的横向经度为ΚOt在横向赤道平面上的投影ΜΚ与-xe轴的夹角λ2,横向经、纬度相同的点的连线为横向子午圈和横向纬线圈。横向地理坐标系的天向即-zt轴方向沿ΚOt向上指向天向,横向地理坐标系的北向即-yt方向沿ΜΚOt平面与当地水平面的交线方向指向横向北,过Ot与横向赤道面平行的平面与当地水平面的交线方向为横向地理坐标系的东向即-xt方向,三轴构成右手坐标系[8]。
椭球体模型下,地心垂线并非与地理垂线处处重合,第一种定义以地心纬度为当地纬度,所建立的横向地理坐标系并非当地水平坐标系,在纬度为80°时,OeOt与ΚOt之间的夹角达到4.14角分,由垂线定义产生的平台倾角误差将远远大于采用圆球体模型引起的倾角误差,由于惯性导航系统的高度通道是发散的,因此在该定义下的机械编排是不稳定的[5,10]。
第二种横向经纬度定义下的横向地理坐标系虽然为当地水平坐标系,但由图4可以看出,由于地理垂线与地球极轴的交点K随载体位置的不同而不断变化,所以沿同一横向子午圈其横向北向也将不断改变,因此在该定义下,横向子午圈并非航向基准,其航向基准为-xt轴方向即本初子午面与当地水平面的交线方向,其本质为格网导航法,其真北向与横向北向的夹角为
由上式可知,其位于真北极点时的夹角为0,其物理意义表示真北极点的北向指向横向北极点,这显然是不符合客观事实的,显然在该定义下,系统不能平稳的经过极点,其误差会发生跳变。该系统将横向坐标系看作一种特殊的游移方位坐标系,因此其机械编排与游移方位系统的机械编排非常类似,其所存在的问题也与游移方位系统一样,即在通过极点时存在物理奇点。引起这一问题的原因在于在该定义下,横向坐标系中的惯性导航参量并不能独立得到,而需要借助传统经纬度坐标系中的惯性导航参量作为中间量解算得到。
4 结语
横向坐标系惯性导航的主要目的在于将坐标系横置,利用横向坐标系中的惯性导航参数进行导航信息的解算,从而摆脱对经线航向基准的依赖,解决由于经线收敛而导致的在极区无航向基准可利用的问题。若使用椭球体模型,从上文分析可以看出,由于旋转椭球体的不对称性,因此在横向经纬度的定义上存在困难。采用垂线定义法,其本质为格网导航法,一种特殊的游移方位坐标系,无法克服在极点处存在物理奇点的问题。如果仿照传统经纬度来定义横向经纬度,则其因垂线偏角引起的误差将超出可接受的范围。采用基于地球椭球体模型的横向坐标系极区惯性导航,虽然降低了由于地球模型带来的误差,但横向经纬度的定义会引起新的误差。若采用椭球体模型,则需横向坐标系下的经纬度进行定义,减小由于经纬度定义引起的误差。
也可以在近极点地区使用圆球体模型,原因如下:
1)以80°为极区边界,则其在极区范围内的曲率半径最大变化值为2km,相比于地球半径,其误差小于千分之一。
2)圆球体模型对称性好,将坐标系横置后可以直接求取横向坐标系中的导航参数,不存在极点处的物理奇点的问题。
3)采用圆球体模型虽然会导致平台倾角误差以及其他速度误差、航向误差等,但在近极点地区的小范围内其处于可接受的范围内。
若采用圆球体模型还需要对圆球体模型下的极区横向惯导进行仿真验证和误差分析,确定其适用范围,并对传统低纬度惯导和极区惯导之间的切换模式进行研究和分析,保证系统在两种模式下进行平稳切换。
[1]刘文超,卞鸿巍,王荣颖,等.惯导系统横向坐标法导航性能研究[J].武汉大学学报,2015,40(11):1520-1525.
[2]李倩,孙枫,奔粤阳,等.横坐标系捷联惯导系统极区导航及阻尼设计[J].系统工程与电子技术,2014,36(12):2496-2503.
[3]李倩,孙枫,奔粤阳,等.基于横坐标系的捷联惯导系统极区导航方法[J].中国惯性技术学报,2014,22(3):288-295.
[4]张福斌,马朋,王智辉.基于横向坐标系的捷联惯导系统/多普勒速度仪极区组合导航算法[J].兵工学报,2016,37(7):1229-1235.
[5]张汉武,王海波,张萍萍.基于横向地球坐标系的极区惯导机械编排研究[J].舰船电子工程,2016,36(8):68-122.
[6]姚逸卿,徐晓苏,童金武.极区间接横向惯性导航方法[J].中国惯性技术学报,2015,23(1):29-34.
[7]徐晓苏,豆嫚.基于横向地理坐标系的极区惯性导航方法研究[J].华中科技大学学报,2014,42(12):116-121.
[8]豆嫚.基于横向坐标系的极区惯性导航方法研究[D].南京:东南大学,33-34,41.
[9]涂睿,王玮.捷联惯导系统的极区导航算法优化设计[J].计算机仿真,2015,32(8):89-130.
[10]王海波,张汉武,张萍萍,等.一种适用于高纬度船舶导航的横向地球坐标系[J].海洋测绘,2016,36(3):25-28.
[11]陈哲.捷联惯导系统原理[M].北京:宇航出版社,1986:50-51.
[12]C F奥唐纳.惯性导航分析与设计[M].群英,译.北京:国防工业出版社,1972:239-244.
[13]恰耳兹·布洛克斯梅耶.惯性导航系统[M].致学,译.北京:国防工业出版社,1972:123-125.
[14]熊介.椭球大地测量学[M].北京:解放军出版社,1988:14-15.
Analysis of The Influence of The Earth Model of The Transverse Coordinate Polar Inertial Navigation
HAO Yongshuai1ZHOU Aijun2WANG Haibo2
(1.Graduate Management Brigage,Dalian Naval Academy,Dalian116018)(2.Department of Navigation,Dalian Naval Academy,Dalian116018)
The problem of polar inertial navigation is that rapid convergence of the Earth's meridians makes it difficult to establish true heading at high latitudes.Traditional inertial navigation system is unable to complete the task of polar navigation.But the polar inertial navigation mission can be accomplished by using the transverse coordinate system of the earth.This paper analyzes the influence of the earth model on polar inertial navigation system based on transverse earth coordinate system.
transverse coordinate,earth model,transverse longitude and latitude
TN96
10.3969/j.issn.1672-9730.2017.07.010
2017年1月3日,
2017年2月17日
郝勇帅,男,硕士研究生,研究方向:船舶导航技术。周爱军,男,博士,教授,硕士生导师,研究方向:船舶导航技术。王海波,男,高级工程师,研究方向:船舶导航技术。

