基于G M（1，1）模型在成都市商品房价格预测中的应用研究

王 洋，王 咏

（四川交通职业技术学院公共课教学部，成都 611130）

基于G M（1，1）模型在成都市商品房价格预测中的应用研究

王 洋，王 咏

（四川交通职业技术学院公共课教学部，成都 611130）

主要介绍GM（1，1）模型的建模机理，借助该模型对成都市商品房价格进行预测。通过对预测结果进行残差分析，说明该方法的合理性，从而为成都市政府宏观调控商品房价格提供政策性依据。

GM（1，1）；预测；房均价

一、灰色系统理论概述

灰色系统理论基于对少数据、贫信息系统的特征、运行机制和表现行为的分析，揭示少数据、贫信息背景下事物的演化规律，为人类正确认识和把握少数据、贫信息系统提供理论支持。在少数据不确定性背景下，对数据的处理、现象的分析、模型的建立、发展趋势的预测、重大事项的决策等都是灰色系统理论的主要技术内容。

灰色预测是整个灰色系统理论的重要组成部分。建立灰色动态模型则是灰色预测理论的核心。灰色预测通过原始数据的处理和灰色模型的建立，发现、掌握系统发展规律，对系统的未来状态做出科学的定量预测。

二、GM（1，1）预测模型

GM（1，1）建模通过对原始数据的处理来找出数据的规律，从而建立微分方程预测模型，对数据值进行拟合，最终确定一系列的预测值。

则定义x（1）的灰导数为：

GM（1，1）模型是一个包含单变量的一阶微分方程构成的动态模型：

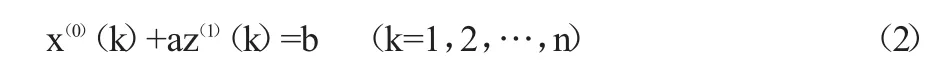
其中，a称为发展系数，b称为灰作用量。

采用最小二乘法，通过计算可以得到：

其中：

对方程求解，即时间响应式为：

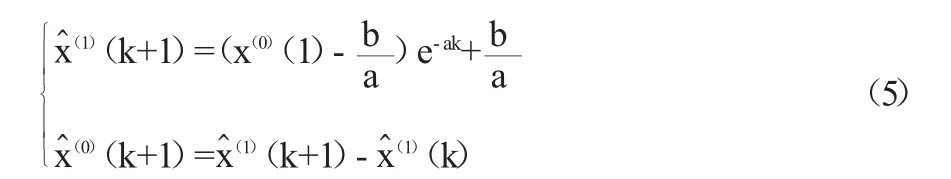
最后进行残差检验，经过检验，合格的模型即可用于预测。假定ε（k）为残差值，则：

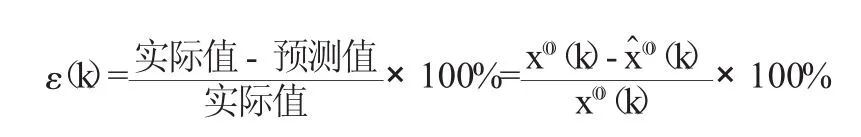
假定精度为p，则p=（1-ε（avg））×100%，其中：

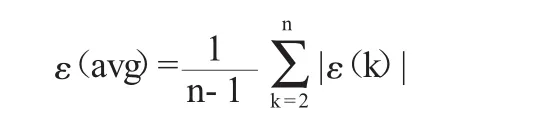
一般要求p＞80%，最好是p＞90%。

三、成都市商品房价格预测

当前对于城市商品房价格的测量还存在较大的争议，本文在这里采用成都市商品房平均销售价格测量成都市总体价格水平的指标。商品房销售价格是通过观测年度内商品房的销售额与销售面积换算而得到的，其计算公式：成都市商品房销售价格=成都市商品房销售总额/成都市商品房销售总面积，数据来自于《四川省统计年鉴》。采用数学软件Matlab进行编程计算，对2015—2016年的成都市商品房价格进行相应的预测。原始数据（见表1）。

通过计算，得到GM（1，1）预测模型为：

表1 成都市2005—2014年商品房价格数据

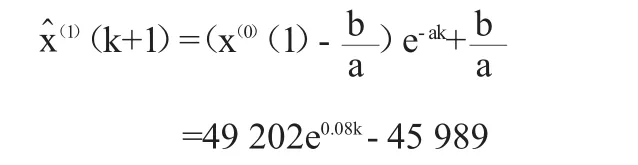
由上面的预测模型可以计算2005—2016年成都市商品房价格的预测值（见表2）。

根据残差检验，可以得出精度p=93.44%，说明预测效果较好。

表2 成都市2005—2016年商品房价格预测数据

四、结论

通过残差检验计算出精度为p=93.44%，从而说明采用灰色GM（1，1）模型进行预测，效果较为理想。通过对成都市商品房价格做出科学的预测和分析，可以保证当地政府的相关职能部门站在合理的角度制定出有利于房地产市场健康稳定发展的政策。不足之处是，当数据离散程度越大，预测精度越差，而且不太适合于时序数据长期后推若干年的预测。

[1]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002.

[2]罗晓玲，周建新，等.基于GM（1，1）模型在高校招生人数预测中的应用研究[J].贵州大学学报，2008，(4).

[3]李敏，王洋.基于灰色系统理论对成都市房价预测分析[J].云南民族大学学报，2013，(6).

[4]曹殿立，何春花，李小芳.基于灰色线性回归组合预测模型的河南省国内生产总值预测[J].河南农业大学学报，2008，(8).

[5]徐国祥.统计预测和决策[M].上海：上海财经大学出版社，2005.

[责任编辑 刘兆峰]

F293.3

A

1673-291X（2017）21-0099-02

2017-02-07

王洋（1985-），男，安徽淮南人，讲师，博士研究生，从事应用数学研究。