电子辐照电介质样品带电泄放弛豫特性研究∗

封国宝 曹猛 崔万照李军 刘纯亮 王芳

1)(中国空间技术研究院西安分院,国家级空间微波技术重点实验室,西安 710000)

2)(西安交通大学,电子物理与器件教育部重点实验室,西安 710049)

(2016年9月13日收到;2016年12月20日收到修改稿)

电子辐照电介质样品带电泄放弛豫特性研究∗

封国宝1)2)曹猛2)崔万照1)†李军1)刘纯亮2)王芳2)

1)(中国空间技术研究院西安分院,国家级空间微波技术重点实验室,西安 710000)

2)(西安交通大学,电子物理与器件教育部重点实验室,西安 710049)

(2016年9月13日收到;2016年12月20日收到修改稿)

电子照射电介质材料的带电效应对介质微波部件的微放电现象有着重要影响.本文采用数值模拟的方法研究电子照射介质样品带电后的弛豫泄放过程.对入射电子与样品的相互作用考虑了弹性和非弹性碰撞过程,采用蒙特卡罗方法进行数值模拟;对沉积在样品内部的电荷泄漏过程则采用考虑电荷迁移、扩散以及俘获等过程的时域有限差分法进行处理.模拟了介质样品在带电泄放弛豫过程中的内部电荷和电位分布以及弛豫暂态特性,并分析了包括样品厚度、电子迁移率以及俘获密度在内的样品参数对泄放弛豫过程的影响.计算结果表明:在介质样品带电泄放的弛豫过程中,样品内部的总电荷量和表面电位逐渐减弱到一个与俘获密度直接相关的终态值;迁移率的增大会类线性比例地减少泄放时间常数,电荷泄放量随着样品厚度的增加呈现先增后减的趋势,而泄放量比随俘获密度增大从1近指数关系地减小为零.

带电泄放,电子辐照,介质材料,数值模拟

1 引 言

电子在航天微波部件内部所产生的二次电子倍增效应会引起器件的微放电现象[1].航天器载荷中微波部件,如输出多工器、波导系统、高频电缆、滤波器、开关矩阵、天线馈源等极易产生微放电效应,从而可能导致噪声电平抬高、输出功率下降、微波传输系统驻波比增大、反射功率增加、信道阻塞[2].微放电效应也会使放电表面发生侵蚀现象,从而使器件性能逐渐变差,有效载荷性能下降,甚至航天器载荷永久失效[3].

随着微波器件大功率和集成化要求的提高,介质微波部件及内部的微放电现象受到更为广泛的关注.然而,不同于导电性较高的金属材料,对于受电子入射的介质材料来说,由于入射和出射电子的不平衡会使得内部产生沉积电荷[4].这种辐照引起的介质带电会改变微波部件的空间电场,同时会对介质微波部件的微放电现象产生更为复杂的影响.

电介质样品会在电子的入射作用下产生表面带电现象,对于下表面接地的样品,样品的带电会随着入射电子的停止和电荷的持续泄漏而逐渐减弱,进行样品的弛豫泄放过程[5].对于导电性不高的介质材料而言,由进出电子的不平衡所带来的净电荷并不能很顺畅地从样品中导通出去.因此,内部电荷的泄漏能力成为影响样品带电状态的重要因素.

在以往的实验测量研究中更多地关注于样品泄放阶段流经样品的各电流的变化,而对于样品电位、内部电场以及电荷分布等相关微观物理量很难直接测量,相关的电子照射介质样品的弛豫泄放特性的数值研究仍然缺乏.

本文采用数值模拟方法,研究了电子辐照电介质样品后的泄放弛豫暂态特性,建立了较为完备的数值物理模型.其中,对入射电子与样品的相互作用考虑了电子与材料弹性和非弹性散射碰撞过程,采用蒙特卡罗(Monte Carlo,MC)方法来处理;而对样品内部电荷的泄漏输运过程则采用考虑电荷迁移、扩散、俘获等复杂过程的时域有限差分(finite-diff erence time-domain,FDTD)法来处理.模拟了介质样品在辐照后的泄放弛豫过程中内部的电荷、电位以及电场等微观暂态变化过程;研究了在泄放弛豫过程中介质样品带电各微观量分布及其受包括样品厚度、电子迁移率以及缺陷俘获密度在内的材料样品参数的影响.本数值研究的方法以及结果对介质微波部件带电的抑制以及介质微波部件的微泄放过程的深入研究具有重要的指导意义.

2 模型及方法

当电子以一定能量入射到样品时,首先会与样品内材料发生包括电子散射和电荷输运等在内的一系列复杂过程.考虑到MC方法在计算机大量随机事件模拟上的适应性[6],且该方法已经被广泛应用于凝聚态物理、应用物理、理论物理、化学以及非线性现象等诸多领域的理论研究和分析中[7],并成为科学研究的一种标准手段,本文采用基于MC方法和FDTD方法分别进行电子散射和电荷输运过程的模拟.电子打入样品材料后,会发生弹性和非弹性碰撞过程,并且表层的电子克服功函数离开样品会形成出射二次电子;此外,沉积在样品内部的电荷则会发生输运过程,如图1.由于本文研究的入射电子均为10 keV以下,弹性散射过程采用Mott散射模型;而非弹性散射则采用Penn介电函数模型和快二次电子模型[8].在内部电荷的输运过程中,考虑了包括电荷密度梯度作用下的电荷扩散、内自建电场作用下的电荷迁移以及样品材料本身缺陷所造成的电荷俘获过程.

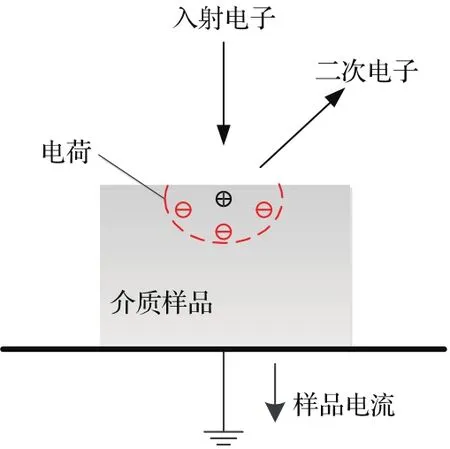
图1 (网刊彩色)电子辐照介质样品示意图Fig.1.(color on line)Schem atic d iagram of electonbeam irrad iation.

2.1 入射电子的散射模型

电子在材料内部行进的过程中会不可避免地与原子或分子发生碰撞,而这种碰撞会使得电子按照某种规律而改变运动轨迹,这个过程称之为散射.电子的散射过程可以根据能量是否损耗分为弹性散射和非弹性散射.弹性散射是原子核和核外电子云的库仑势对电子的散射.由于原子核的质量远远大于电子的质量(大三个数量级以上),原子和入射电子在散射前后的能量改变均可以忽略不计,只是入射电子的运动方向发生了变化.而在非弹性散射过程中,入射电子在散射前后不仅运动方向发生了变化,而且能量也有一定损失.

要分析电子的散射过程,首先需要计算电子的散射截面.电子的散射截面根据散射类型的不同,同样分为弹性散射截面和非弹性散射截面.入射电子的弹性散射截面是入射电子的微分弹性散射截面对各个方向的积分,而入射电子的非弹性散射截面则是入射电子的微分非弹性散射截面对各个方向和各种能量损失的积分.其中,微分弹性散射截面是入射电子弹性散射到某一方向单位立体角Ω内的概率dσe/dΩ,总的弹性散射截面σe为入射电子的微分弹性散射截面对各个方向的积分,

而原子的非弹性散射截面σin是原子的微分非弹性散射在所有立体角Ω和所有入射电子终态能量Ef范围内的双重积分,即

2.1.1 弹性散射

对于不同能量EPE的入射电子的弹性散射过程,可以采用不同的散射截面来描述.对于高能量的入射电子(EPE＞10 keV),在描述电子弹性散射模型时,在Born近似下,可以通过求解Schrodinger方程得到微分散射截面,即Rutherford弹性散射模型.而对于入射电子能量较低(EPE＜10 keV)时, Born近似已不再成立,准确的微分弹性散射截面应该由相对论的狄拉克方程导出,即采用散射分波法得到数学表达式.因此,针对本文研究的入射电子能量在10 keV以下的条件,采用Mott散射模型来计算微分散射截面[9].Mott弹性散射是与自旋有关的电子弹性散射理论,入射电子的初始平面波在传递的过程中有各自的相移,而对应的散射振幅为分波的求和,因此M ott微分弹性散射截面可以表示为[10]

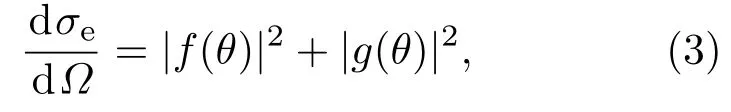
其中,σe为弹性散射截面(单位:cm2·atom−1),Ω为立体角(单位:(◦)),θ为散射角.f(θ)和g(θ)为入射分波函数和散射分波函数,可以通过分波法求得:

其中,求和号中的l=0,1,2,···,∞是分波的编号;i表示虚数;Pl(cosθ)和P1l(cosθ)分别是Legendre函数和一阶联立Legendre函数;各分波的相移ηl,η−l−1由中心势场Dirac方程的径向解得到;K为入射能量与静止电子质能Eme的相关量; K2=(EPE/Eme)2−1.

对M ott微分散射截面在各个方向上θ∈[0,π]积分便可以得到M ott弹性散射的总散射截面:

2.1.2 非弹性散射模型

除了无能量损耗的弹性散射,电子与样品材料还会发生有能量损耗的非弹性散射过程.为了提高模型的准确性,本文对非弹性散射模型在不同电子能量段采用不同的非弹性散射模型.对于能量高于3 keV的电子采用快二次电子模型来模拟非弹性散射过程[11],而当能量低于3 keV时,更适合用Penn介电函数模型来处理[8].

1)快二次电子模型

对于快二次电子模型,电子与样品在非弹性散射过程中考虑量子力学的微分散射截面dσin/dΩ为[12]

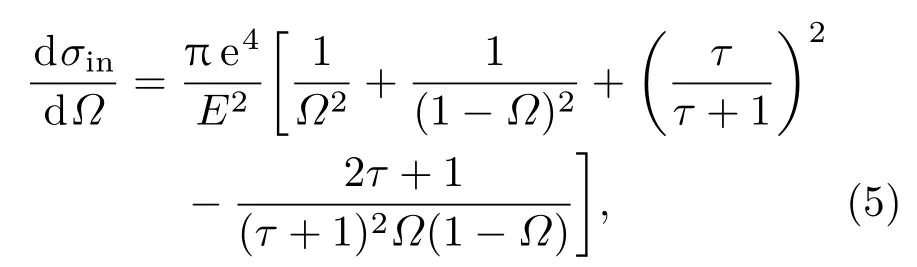
其中,e为基元电子电荷;E为电子能量;Ω为归一化的能量损失系数,即损失能量与散射前电子能量之比;τ为电子的动能与静止质能比.

对于非弹性散射过程中的能量损耗,快二次电子模型采用Joy[13]修正的Bethe能量损失公式来处理.电子在单位长度d S内的能量损失为

其中,Z为材料原子序数,A为原子质量(g·mol−1), ρ为材料密度(g·cm−3),J为材料的平均电离能(keV),kZ原子序数Z相关的电离能修正系数.对于化合物材料,以上的原子序数Z、原子质量A以及平均电离能J为各种元素的权重平均.

2)Penn介电函数模型

对于低能入射电子(EPE＜3 keV),Penn[8]提出的基于光学常数的介电函数模型更加适用于介质在低能电子束照射下的非弹性散射问题[14].由于介质中的电子非弹性散射主要与价电子激发相关(内壳层电子激发仅占极少部分,可以忽略),因此可以使用介电函数理论来得到其非弹性散射截面.但是,在实际中与动量转移及能量损失ħω相关的介电函数ε(0,ħω)往往难以得到.Penn[8]提出,通过将实验光学常数扩展到未知的动量转移区域就可以求得相应的介电函数.本研究即采用Penn介电函数模型来计算低能入射电子(EPE＜3 keV)的非弹性散射截面.对应的非弹性微分散射截面为

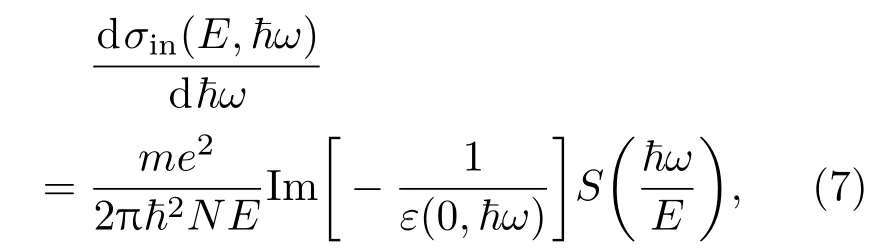
其中,m为电子质量,N为材料的分子数密度,Im表示函数的虚部,ħ为约化普朗克常量.式中的S(ħω/E)函数,可以根据Ashley的理论简化求得.

在Penn模型中除了考虑电子与电子的相互作用,还考虑了电子与声子的相互作用.在入射电子能量低于数个材料禁带宽度时,电子与声子相互作用的概率会快速增加.根据Fröhlich和M itra[15]的理论,对于一个能量为E的电子,其与晶格振动相互作用,产生一个能量为ħω的纵向光学声子(根据能量守恒,电子的能量损失也为ħω)的平均自由程的倒数为

式中,a0为玻尔半径,kB为玻尔兹曼常数,ε(0)和ε(∞)分别为材料的静态介电常数和高频介电常数.电子与声子相互作用的能量损失的取值为Wph=ħω=0.1 eV.

此外,Penn模型中还考虑了低能电子将受自身附近所产生的感应极化场的极化子效应.根据Ganachaud和Mokrani[16]的理论,低能电子由于极化子效应而被离子晶格所俘获的平均自由程的倒数为

式中,C和γ均为与材料特性相关的常数.并根据Ganachaud和M okrani的假设,当低能电子产生极化子,电子剩余的能量几乎可以被忽略,从而相当于被俘获.

由于在Penn介电函数模型中考虑了电子与电子、声子以及极化子作用,因此,首先需要判断是发生了哪一种非弹性散射作用.本文采用Penn模型下非弹性散射的总平均自由程的倒数来判断,

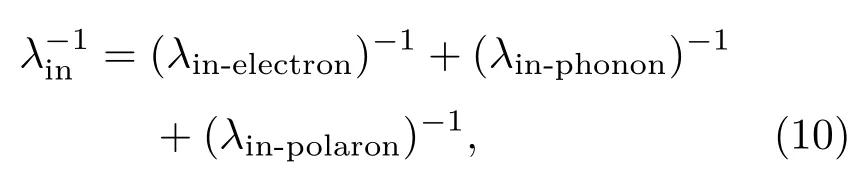
并求出每一种散射所发生的概率λin/λin-electron, λin/λin-phonon和λin/λin-p olaron,并通过一个随机数Rin-Penn来判断发生哪一种散射过程.

2.2 电荷输运模型

在散射过程中沉积在样品内部的电荷会在自建电场和电荷浓度梯度的作用下发生电荷的输运[17].从微观上说,沉积在样品内的自由电子会在样品内部积累的静电荷所产生的电场和电荷梯度场作用下发生迁移和扩散.此外,在电子迁移和扩散的过程中,由于材料本身缺陷的存在,会使得一部分自由电子被俘获中心俘获[18].

如图2所示,电子非穿透辐照介质薄膜样品的带电过程需要考虑入射电子的散射过程和内部电荷的输运过程.当能量为EPE的电子进入样品后,会与样品内部的原子产生弹性和非弹性散射,激发产生内二次电子和空穴对,一部分内二次电子脱离表面以二次电子的形式出射,形成二次电子电流JSE.同时,样品内的电荷会在自建电场和电荷浓度梯度的作用下向样品底部输运,形成传输电流JE.在电子向样品底部输运的过程中,由于样品内部缺陷的存在,部分自由电子会被样品内的缺陷俘获形成俘获电子.而未被俘获的自由电荷到达样品底部后形成泄漏电流JL.此外,根据电流连续性原理,金属接地板的底部会因为感应电场而产生感应电流JD.对于接地型的金属下极板,实际测量的样品电流JS为泄漏电流与感应电流之和: JS=JD+JL.

本文针对实验环境中常用的入射电子能量大于第二临界能量的条件,研究被广泛关注的介质样品的负带电现象.在负带电情况(表面电位小于零, VS＜0),由于样品内部的空穴数量小于电子数量,并且被束缚在浅表层附近,所以在模拟样品带电过程时可以只考虑等效负电荷(净电子)的散射积累以及输运迁移.

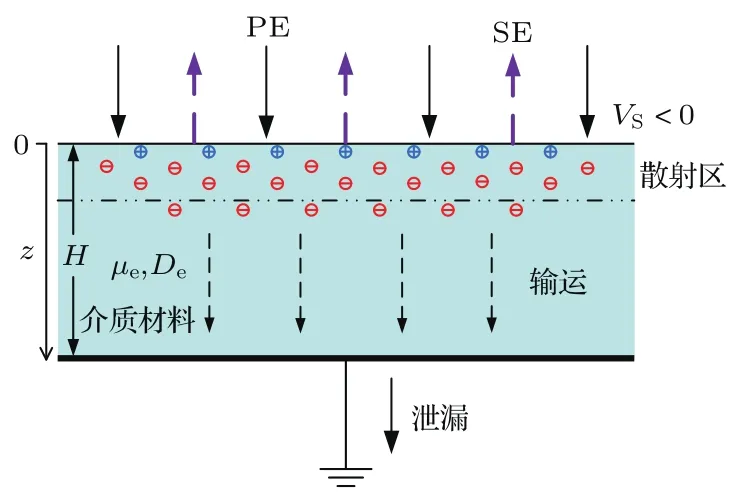
图2 (网刊彩色)电子辐照电介质样品带电过程的示意图Fig.2.(color on line)Schem atic d iagram of dielectric sam p le charging p rocess due to electron-beam irrad iation.

在输运过程中,样品内部的自由电子密度nF(z,t)、 俘获电子密度ntrap(z,t)和空间电位V(z,t)满足电流连续性方程、电荷输运方程、俘获方程以及泊松方程:

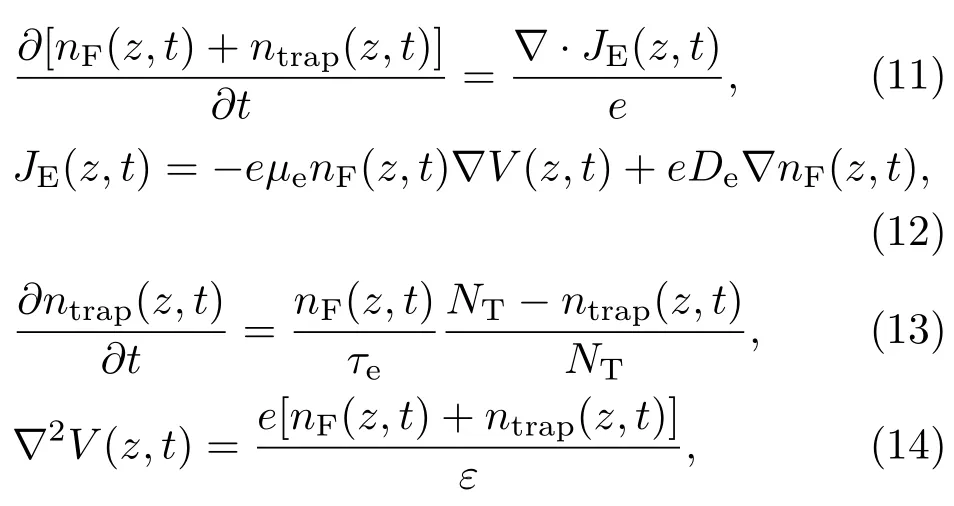
式中,NT为样品材料的俘获密度(cm−3);τe为俘获时间常数(s);e为单个电子电量;ε为相对介电常数;µe和De分别为介质材料的电子迁移率和扩散系数,并满足Nernst-Einstein方程De=µekBT/e,其中kB为玻尔兹曼常数,在本文中温度T=300 K.

此外,在带电模拟中,样品内的暂态总电荷量密度Q(ti)可以通过时域电荷守恒或者z方向的空间电荷密度积分求得:

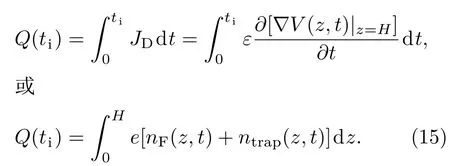
2.3 泄放弛豫模拟流程

上述的模拟描述了样品在电子持续辐照时,电子在散射过程中的电荷沉积以及在输运过程中的电荷迁移,样品的总带电量呈现一种逐渐积累的充电过程.然后,当电子辐照一段时间后停止,没有外在进入的净电荷,而内部的电荷也将逐渐输运到样品底部泄漏而减少,形成一个泄放的过程.

图3为样品在电子辐照持续后的泄放过程的模拟流程图,具体的流程如下.

1)散射过程的电荷积累.在散射过程中,由于入射的电子多于出射的二次电子,内部的电荷在弹性散射和非弹性散射作用下,最终产生大量的沉积电荷d Q scat|Δt.

2)电荷的输运.随着散射电荷的逐渐沉积,总电荷增加,Qt=Qt+d Qscat|Δt.并且,开始下一步的电荷输运过程,使得电荷分布发生变化.

3)时域的循环迭代.样品内部的电荷在输运过程后,又一次进入下一次散射沉积电荷的叠加,并循环进行,直到充电达到饱和或者电子辐射停止.

4)当入射电子停止辐照之后,样品内的电荷不再有外加的沉积电荷,此时d Qscat|Δt=0.内部的电荷只是在输运的过程中逐渐向底部泄漏,直到内部的自由电子全部泄漏完全,样品内的带电基本不再变化,最终结束泄放过程.

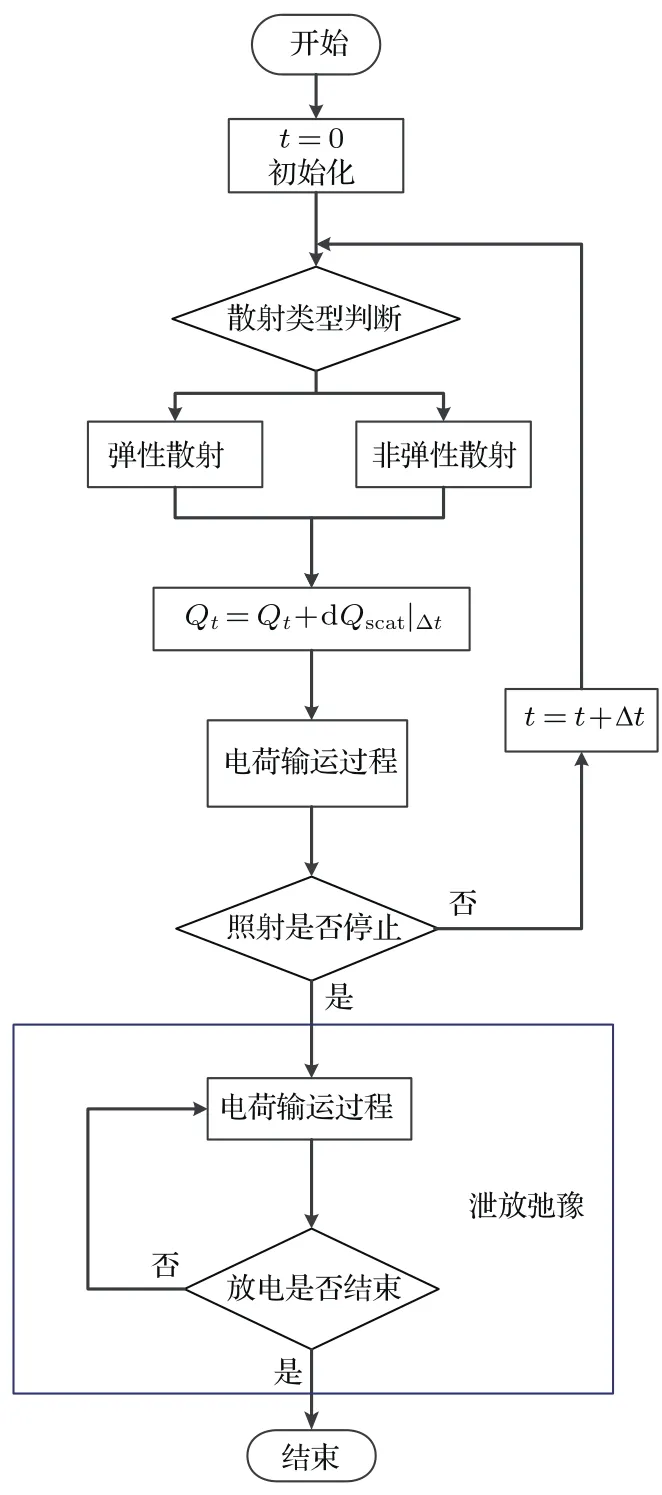
图3 样品泄放的数值模拟流程图Fig.3.F low d iagram of sam p le d ischarge sim u lation.

3 结果与分析

在本文中,样品材料选用电子迁移率较低、带电较强的聚合物材料聚甲基丙烯酸甲酯[19].在本文的数值模拟中,如未做说明缺省参数设置如表1所列.

入射电子的辐照使得样品带电,发生充电过程,而当照射停止后,内部的电荷(以自由电子为主)会在内建电场和梯度场的作用下继续输运和泄漏,发生照射中断后的泄放过程.由于当电子持续辐照介质样品使得其带电达到饱和,进出样品的电流达到平衡,样品内的带电状态也不再变化.因此,在本文中我们假设入射电子的中断发生在样品充电达到饱和之后.在实际的模拟过程中,考虑到带电饱和的过程感应电流JD只会无限接近于零,因此,本文认为当感应电流达到一个较小的阈值时JD＜0.005JPE则达到带电平衡.

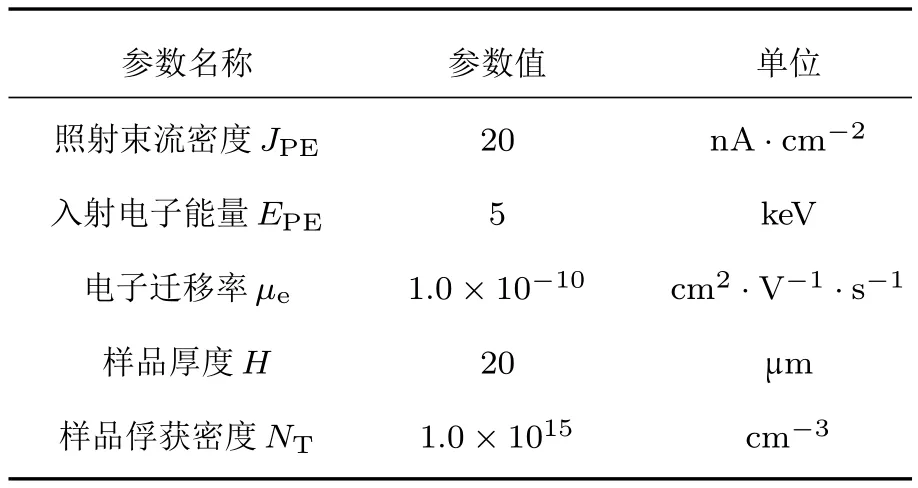
表1 带电暂态过程模拟的默认参数设置Tab le 1.Values of paranm eters in simu lation.

3.1 样品泄放的暂态过程

1)内部分布

入射电子照射停止后,样品不再有散射电荷的沉积,而电荷的输运过程由于内建电场和内部电荷的存在将继续进行.图4为泄放过程不同时刻样品内的总电子密度和自由电子密度的分布.由于俘获电荷被缺陷中心束缚,并不会发生迁移和扩散过程.因此,在泄放过程的电荷输运和泄漏主要为自由电子的变化过程.而总电荷分布在泄放过程的变化规律也基本与自由电子的变化规律一致.如图4(b),从10—80 s时刻,内部的自由电子随着泄漏的进行逐渐减小.并且,由于散射作用的减去,内部电荷的峰值也逐渐向样品深度方向移动.随着自由电子的完全泄漏,最终样品内部的总电子几乎完全由俘获电子构成.

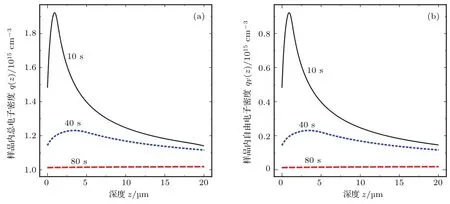
图4 泄放过程不同时刻样品内的电荷分布 (a)总电子密度;(b)自由电子密度Fig.4.Inthernal charge d istribution at diff erent tim es:(a)Total electron density;(b)free electron density.

图5 泄放过程不同时刻,(a)样品内电场和(b)电位的分布Fig.5.(a)Internal E-field and(b)potential d istribu tion at diff erent tim es.

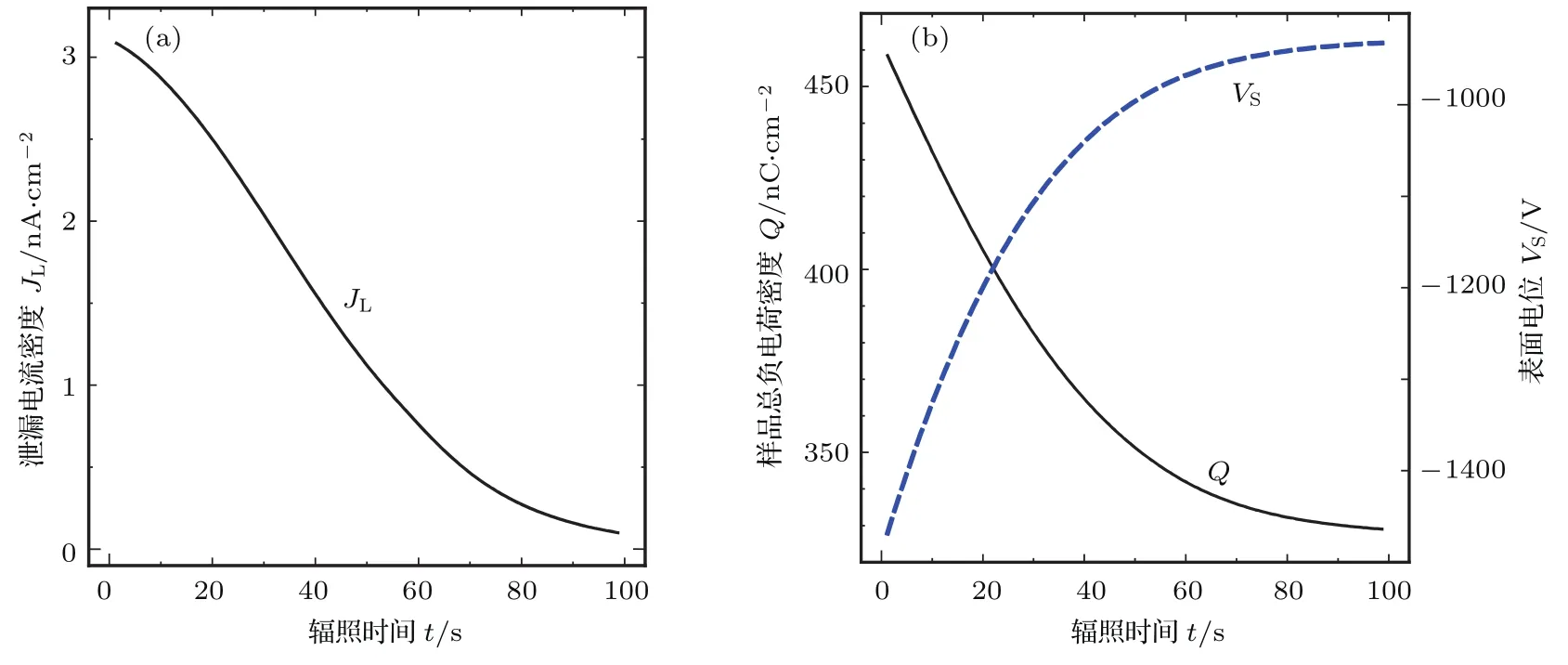
图6 泄放过程中样品底部的(a)泄漏电流和(b)总电量以及表面电位的暂态变化曲线Fig.6.Transient of(a)leakage cu rrent,(b)total charge quantity and su rface potential during discharge p rocess.

同时,内部自由电子的逐渐泄漏也会相应地使内部的电场和电位减弱.图5为泄放过程不同时刻样品内部电场EF(z)和电位V(z)的分布情况.在泄放过程中,从t=10 s时刻到t=80 s时刻,样品内部电场EF(z)和电位V(z)呈现整体减弱过程.然而,同样由于内部俘获电荷的存在,内部的电场和电位仍然存在一定的余量.

2)时变特性

在泄放过程中,由于入射电子的停止,入射电子电流和二次电子电流不再存在,JPE=0, JSE=0.此时,只需要考虑样品的泄漏电流JL.同时,随着电荷的逐渐泄漏,样品内的总负电荷和表面电位也将逐渐减弱.图6即为泄放过程中泄漏电流和表面电位VS以及总电荷量Q的暂态变化过程.

3.2 样品参数对泄放暂态的影响

在电子辐照停止后的样品泄放过程中由于没有电子的散射过程,内部的带电变化过程主要为电荷的输运和泄漏.因此,下文主要分析输运相关的样品电子迁移率、样品厚度以及材料的俘获密度对泄放暂态过程的影响.考虑到泄放过程发生于样品充电饱和后,而不同的样品参数条件下带电的饱和状态也不同,因此,泄放的暂态过程在不同参数条件下的初始状态也会因为参数对充电过程的影响而不同.

3.2.1 电子迁移率

样品的电子迁移率影响自由电子在样品内迁移和扩散的速度,从而影响泄放过程电荷的输运和泄漏的快慢.图7为三种不同样品电子迁移率(µe=10−11,10−10和10−9cm2·V−1·s−1)下,样品达到带电饱和并停止照射后的泄放暂态过程.对于泄漏电流JL,在电子迁移率相对较大时(如µe=10−9cm2·V−1·s−1),泄漏电流在泄放阶段从较高的饱和值迅速下降为零,而当电子迁移率变小时,电荷的泄漏过程将逐渐放缓.与表面电位VS暂态过程类似,样品内的总负电荷在迁移率较小情况下从一个较大的初始值更为缓慢地下降,并最终达到一个基本相同的最终值.

此外,根据上文对带电泄放过程终点阈值的定义,模拟了在不同材料电子迁移率情况下的泄放时间常数Td,如图7(d)所示.泄放过程的时间常数随着迁移率的增大而缩短,其对数表现出类线性关系:

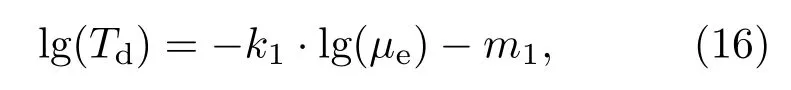
式中,k1表示时间常数Td随电子迁移率增大而缩短的速率,主要与样品厚度、材料缺陷密度等材料特性参量相关,在图7中k1=8.25;而m1则是与带电状态相关的参量,可能与电子散射过程相关,这里m1=6.28.

3.2.2 样品厚度

在泄放的过程中,样品厚度的增加使得内部的自由电子泄漏需要更长的距离,暂态的泄放过程变得更为缓慢.图8为几种不同厚度的样品(H=10, 20,30,40µm),在达到带电平衡后的泄放暂态过程.在厚度更大的样品,泄漏电流密度JL、表面电位VS和样品总负电荷量Q减小更慢.考虑到充电饱和样品总电量随着样品厚度的非单调性变化,因此,在较厚的样品情况下(如H=40µm),泄放的初始值也相应地变小.此外,从图8(c)可以发现,无论饱和状态下的带电量还是最终的带电量都随着厚度的增大先增后减,这主要与带电饱和状态的平衡模式相关[20].并且,如图8(d),泄放量在H=20µm时比H=10µm和H=30µm情况下的泄放量都多,这是由于样品厚度的增加,一方面会增加样品内部的积累电荷的能力,另一方面又会阻碍电荷的泄漏,因此在两者相反的作用下,使得总电荷量在泄放弛豫过程的变化量ΔQ随样品的变厚出现先增后减的非单调性变化,而对应的泄放量比却持续减少.

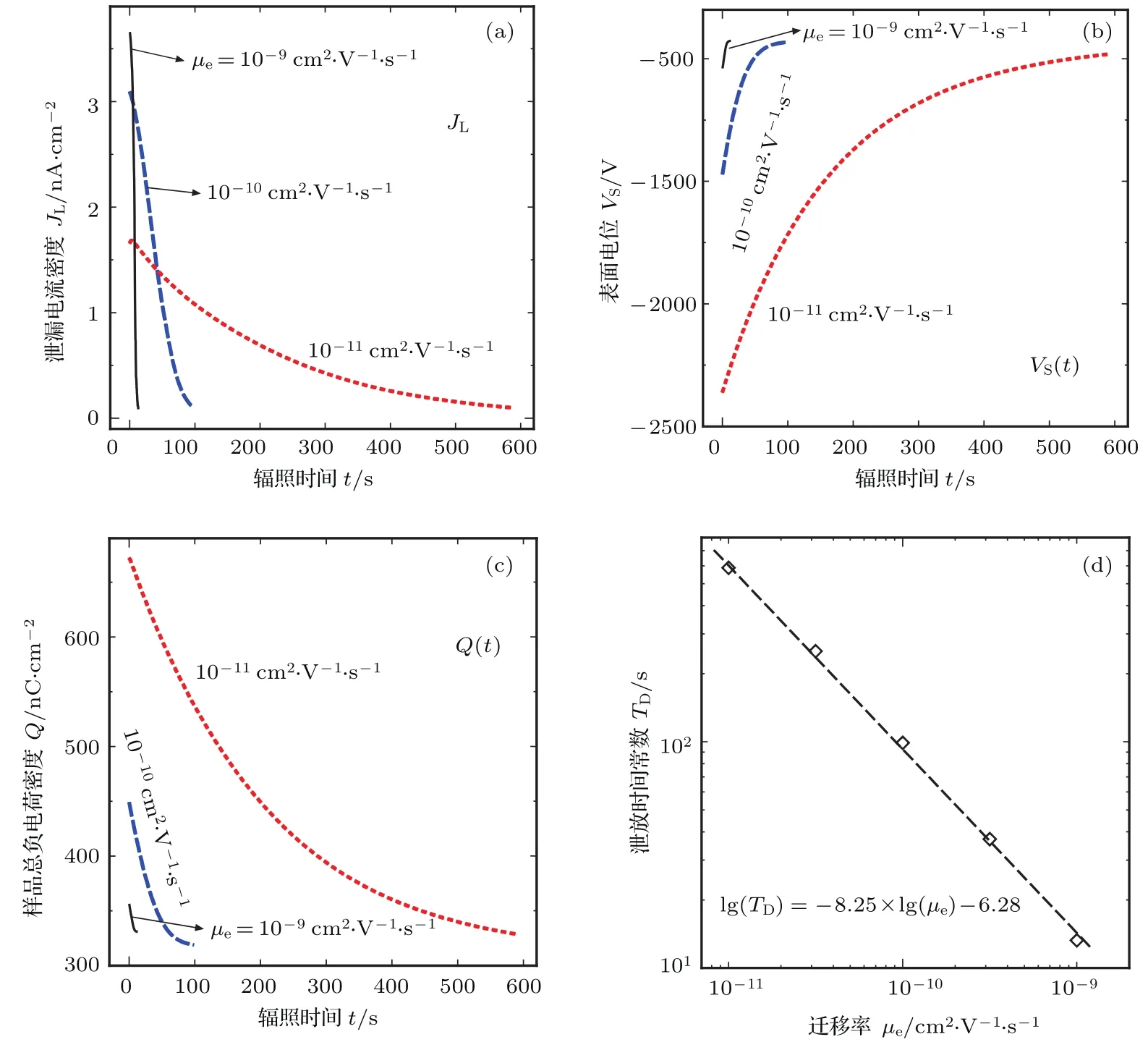
图7 电子迁移率对泄放相关暂态特性的影响 (a)泄漏电流密度;(b)表面电位;(c)样品总电荷量;(d)时间常数Fig.7.E ff ect of electron m obility on discharge transient:(a)Leakage current;(b)su rface potential;(c)total charge quantity;(d)tim e constant.

3.2.3 俘获密度

材料的俘获密度的变化会影响样品内被俘获的自由电子数量,相应地影响泄放过程中自由电子的输运过程.图9为不同材料俘获密度下(NT=5×1014,1×1015,2×1015cm−3),样品内各带电特征量的暂态过程.对于缺陷俘获密度更大的材料,样品内的自由电子更容易被俘获形成被束缚的俘获电子,这样最终能从样品中泄漏的自由电子将减少.因而在图9中,泄漏电流更大的样品(如NT=2×1015cm−3),泄漏电流密度JL、表面电位VS和样品总负电荷量Q在泄放的过程中变化量更小.同时,由于俘获密度更小的样品在泄放过程中需要泄漏更多的电荷,并且俘获密度更小的样品在充电过程中积累的总带电更弱,导致自由电子输运的速度更慢,因此俘获密度更小的样品泄放过程更长.此外,在电荷的泄放过程中,电荷的泄放量d Q以及泄放比PdQ(泄放量与总初始电量比PdQ=d Q/Q)都会随着材料俘获密度的增大而减少,如图9(d),泄放量比与俘获密度表现出指数关系:式中,a是影响泄放比随俘获密度减少的参量,由带电饱和状态下电荷分布决定,是一个与辐照入射参数以及相关材料参数均有关系的复合变量, a=fa(EPE,JPE,H,µe),在图9条件下,a=1.23.样品内电荷泄放比随着材料俘获密度的增大,近指数地从1减小,趋向于零.

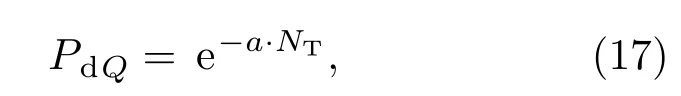
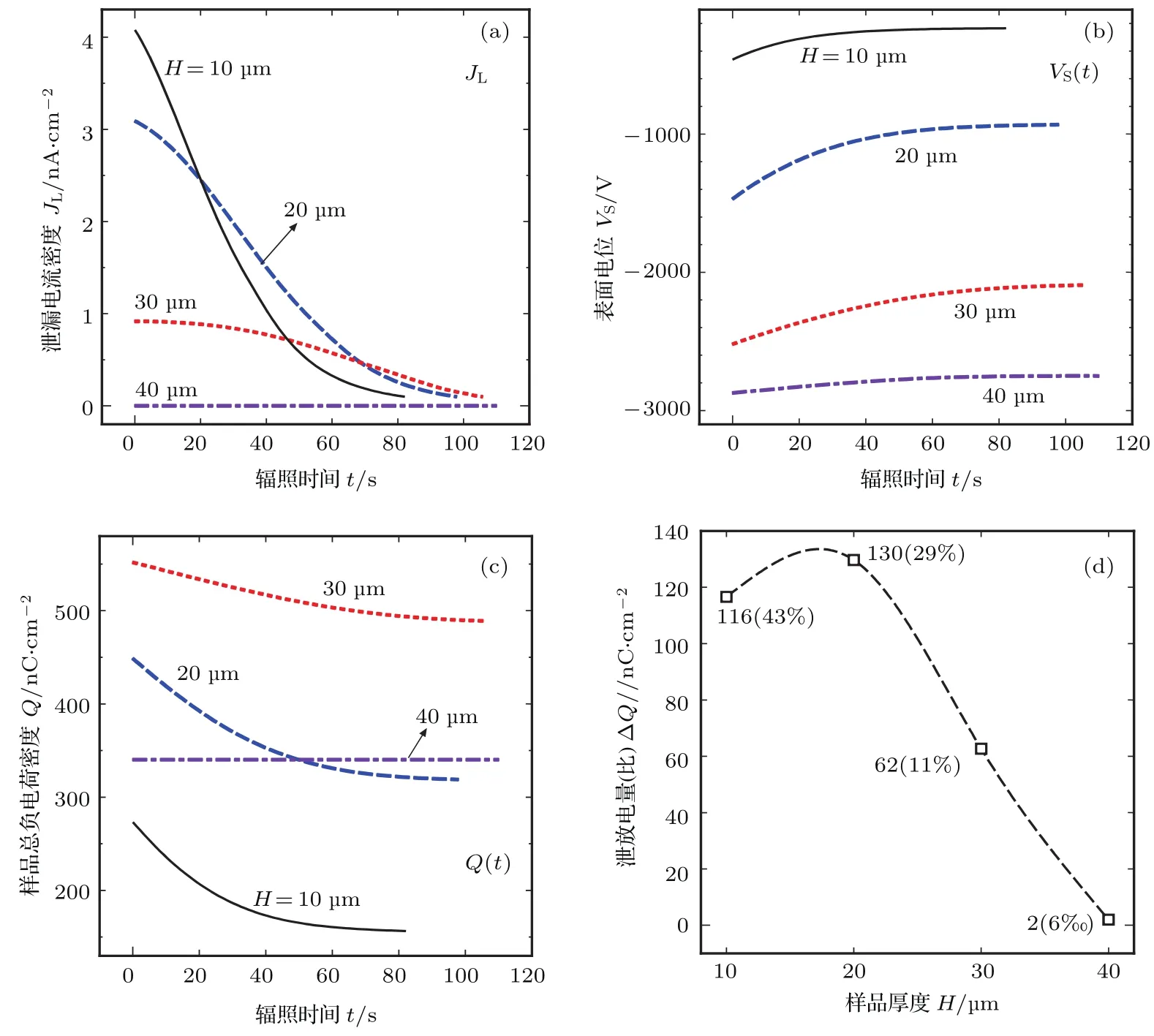
图8 样品厚度对泄放相关暂态特性的影响 (a)泄漏电流密度;(b)表面电位;(c)样品总电荷量;(d)泄放电量Fig.8.E ff ect of sam p le thickness on d ischarge transient:(a)Leakage current;(b)surface potential;(c)total charge quantity;(d)d ischarge quantity.

4 讨 论

本文分析的泄放弛豫过程是发生在辐照样品带电饱和以后,相比于人为构造相同的带电状态下进行泄放弛豫过程的研究,本文的研究更贴合实际情况.这是因为各种材料参数除了会影响泄放弛豫过程,还会对带电过程产生影响[20].

材料迁移率的增大虽然使得样品在泄放阶段的泄放量减小,但由于大的电子迁移率意味着大的电子迁移速度,因此也使得内部电荷泄放的速度更快.同时,更大迁移率的样品在泄放过程中带电强度都表现得更弱,因此要避免带电的影响,可以采用电子迁移率更大的材料,或者采用金属掺杂的电介质材料.在图8中,样品总泄放量随着厚度的增大先增后减,这是由于样品厚度的增大在增加总电荷体量的同时阻碍了电荷泄漏.除此之外,这种总电荷量随着厚度先增后减的趋势还可能受到进出样品电流的平衡模式的改变的影响[21],其具体的机理和规律还有待进一步的研究.材料缺陷所产生的电荷俘获可对电荷的泄放过程产生非常显著的影响.由于俘获的电荷很难逃逸,使得泄放弛豫过程最终剩余的电荷主要由俘获电荷组成,并且俘获密度的大小直接决定了泄放过程和最终状态的带电状态.因此,缺陷更小的材料更有利于电荷的泄漏和带电的规避.

图9 俘获密度对泄放相关暂态特性的影响 (a)泄漏电流密度;(b)表面电位;(c)样品总电荷量;(d)泄放电量比Fig.9.E ff ect of trap density on d ischarge transient:(a)Leakage cu rrent;(b)su rface potential;(c)total charge quantity;(d)d ischarge quantity percent.

5 结 论

本文采用数值模拟的方法研究了电介质材料在电子辐照后电荷的弛豫泄放过程.通过建立电子与样品材料相互作用以及内部电荷输运的数值物理模型,研究并分析了样品在饱和带电后的弛豫泄放过程中各带电微观量的暂态变化过程.主要得到以下4点结论:

1)在带电泄放的暂态过程中,样品内部的电荷在近表面处的最大峰值会逐渐向样品底部移动并逐渐减弱,样品内部的总电荷量和表面电位逐渐减弱到一个与俘获密度直接相关的终态值;

2)电子迁移率更大的样品,不仅使得样品的带电更弱,而且在泄放暂态过程中泄漏的电荷量也更少,迁移率的增大会加快在泄放弛豫过程中对应的时间常数会随着迁移率类线性比例地减少;

3)样品厚度的增加虽然会使得内部电荷量的泄放比持续减小,但是对应的电荷泄放量呈现先增后减的趋势;

4)样品内俘获密度的增大会阻碍样品电荷的泄放,泄放的最终带电状态与俘获密度直接相关,对应的泄放量比随俘获密度增大从1近指数关系地减小为零.

总的来说,尽管介质材料的各参数都会影响带电的泄放过程,但具体的影响效果不尽相同:迁移率会更显著地改变泄放时间;材料厚度会使得泄放的初始电量出现逆转的变化趋势;而俘获密度则会指数量级地影响泄放电量比.

[1]Zhang N,CuiW Z,Hu T C,W ang X B 2011 Space E lec. Tech.38 38(in Chinese)[张娜,崔万照,胡天存,王新波2011空间电子技术38 38]

[2]Chen J R,W u X D 1999 Space E lec.Tech.1 19(in Chinese)[陈建荣,吴须大1999空间电子技术1 19]

[3]Sazontov A,Buyanova M,Sem enov V,Rakova E, Vdovicheva N,Anderson D 2005 Astrophys.J.12 053102

[4]Tan C C,Ong K S 2010 Rev.Sci.Instrum.81 064703

[5]K im W,Jun I,Kokorow ski M 2010 IEEE Trans.Nuc. Sci.57 3143

[6]Rubinstein R Y,Ridder A,Vaism an R 2013 Fast Sequential M onte Carlo M ethods for Counting and Optim ization(Hoboken:John W iley Sons,Inc.)

[7]Landau D P,Binder K 2014 A Guide to M onte Carlo Sim u lations in Statistical Physics(New York:Camb ridge University Press)

[8]Penn D R 1987 Phy.Rev.B 35 482

[9]M ott N F,Sir H S,M assey W 1949 The Theory of A tom ic Collisions(Ox ford:C larendon Press)

[10]Czyzew ski Z,M acCallum D O,Rom ig A,Joy D C 1990 J.Appl.Phys.68 3066

[11]Joy D C,Joy C S 1995 M icroscopy M icroanal.1 109

[12]Raczka R,Raczka A 1958 Phys.Rev.110 1469

[13]Joy D C 1995 M on te Carlo M odeling for E lectron M icroscopy and M icroanalysis(New York:Ox ford University Press)

[14]D ing Z J,Shim izu R 1996 Scanning 18 92

[15]Fröh lich H,M itra T K 1968 J.Phys.C 1 548

[16]Ganachaud J P,M okrani A 1995 Surf.Sci.334 329

[17]Fakhfakh S,Jbara O,Fakh fakh Z 2009 IEEE Conf. E lectr.Insu l.D ielectr.Phenom ena 2009 441

[18]Fang Z Q,Hem sky JW,Look D C,M ack M P,M olnar R J,V ia G D 1997 MRS Proceed.482 881

[19]Sessler G M,Figueiredo M T,Ferreira G F L 2004 IEEE Trans.D ielectr.E lectr.Insu l.11 192

[20]Feng G B,Cao M,Yan L P,Zhang H B 2013 M icron 52-53 62

[21]Feng G B,W ang F,Cao M 2015 Acta Phys.Sin.64 227901(in Chinese)[封国宝,王芳,曹猛 2015物理学报64 227901]

Transient characteristics of d ischarge of polym er sam p le after electon-beam irrad iation∗

Feng Guo-Bao1)2)Cao Meng2)CuiWan-Zhao1)†Li Jun1)Liu Chun-Liang2)Wang Fang2)

1)(National Key Laboratory of Science and Technology on Space M icrowave,China Academ y of Space Technology X i’an, X i’an 710000,China)
2)(Key Laboratory for Physical Electronics and Devices of the M inistry of Education,X i’an Jiaotong University, X i’an 710049,China)
(Received 13 Sep tem ber 2016;revised m anuscrip t received 20 Decem ber 2016)

Charging eff ect of dielectric material due to electron beam irradiation has a significant infl uence on them icrodischarge phenom enon of dielectricm icrowave com ponent bymultipactor.The discharge p rocess caused by internalelectron leakage can relieve this undesirable charging eff ect.In this paper,we study the transient discharge characteristics of a dielectric sam p le after being irradiated by electron beam through numerical simulation.Both the charging and discharging processes of a dielectric sam p le are considered w ith a com p rehensive m odel.The M onte-Carlo m ethod is used to simulate the interaction between p rim ary electrons and m aterial atom s before the irradiation is interrupted,including elastic scattering and inelastic scattering.The elastic scattering is calculated w ith the M ott scattering model,and the inelastic scattering is simulated w ith the fast secondary electron m odel or Penn m odel according to electron energy. M eanwhile,the transport p rocess of internal charges in the sam p le during the discharge period is simulated including the charge diff usion under the force of charge density gradient,the drift due to built-in E-field,and the trap caused by material defect.In this work,the discharge process is taken to begin at the very moment of charging reaching saturation,w ith the internal charges kep t alm ost unchanged.A polym er m aterial w idely used in advanced com ponent is considered in thiswork due to its remarkable charging eff ects.Distributions of internal charges of the sam p le during the discharge process are simu lated,and influences of sam p le parameters,including sam p le thickness,electron mobility and trap density in the discharge process,are analyzed.The results show that internal charges m ove to the bottom of the sam p le during the discharging,leading to the surface potential reaching an ultim ate state which is determ ined by trap density of the material.The position corresponding to the maximum internal charge density shifts towards the grounded bottom.A lthough a sam p le w ith a larger electron m obility m eans a faster discharge p rocess,fewer free electrons in this sam p le result in less discharge quantity.The tim e constant of discharge p rocess decreases w ith the increase of sam p le electron mobility in the form of sim ilar linearity.A lthough a sam p le w ith a larger thickness can hold m ore internal charges,the increase of sam p le thicknessm ay increase the distance of internal charges leak yet.Hence,the quantity of discharge fi rst increases and then decreases w ith the increase of sam p le thickness.In addition,a larger trap density of a dielectric sam p lemakes charge leak harder,resulting in a lower discharge quantity.Finally,the p roportion of discharge quantity in saturated charge quantity decreases from 1 to 0 exponentially w ith the increase of sam p le trap density.As a conclusion,those sam p le param eters have their corresponding eff ects on discharge characteristics by m eans of diff erent physicalmechanism s.Sam p le electronmobility determ ines the discharge time constant obviously by aff ecting the electron transport speed.The sam p le thickness aff ects the discharge quantity by shifting the charging balancem ode, and m aterial defect im pedes part of discharge quantity from trapping internal free electrons.This simulation m ethod and resu lts can help to recede the charging eff ect and estimate the evolution charging and discharging states of dielectric m aterial during and after electron beam irradiation.

discharge transient,electon-beam irradiation,dielectricm aterial,numerical simualtionPACS:79.20.Ap,72.20.Dp,02.70.Uu,72.80.Le

10.7498/aps.66.067901

:79.20.Ap,72.20.Dp,02.70.Uu,72.80.Le DOI:10.7498/aps.66.067901

∗国家自然科学基金重点项目(批准号:U 1537211)、中国博士后科学基金(批准号:2016M 602944XB)和空间微波技术重点实验室基金(批准号:9140C530101140C53231,9140C 530101150C53011)资助的课题.

†通信作者.E-m ail:cuiwanzhao@163.com

*Pro ject supported by the K ey Program of National Natu ral Science Foundation of China(G rant No.U 1537211),the China Postdoctoral Science Foundation(G rant No.2016M 602944XB),and the Foundation of National Key Laboratory of Space M icrowave Technology,China(G rant Nos.9140C530101140C53231,9140C530101150C53011).

†Corresponding author.E-m ail:cuiwanzhao@163.com