基于变分模态分解-相干分析的肌间耦合特性∗

杜义浩 齐文靖 邹策 张晋铭 谢博多 谢平†

1)(燕山大学电气工程学院,河北省测试计量技术及仪器重点实验室,秦皇岛 066004)

2)(中国人民解放军第281医院康复医学科,秦皇岛 066100)

(2016年7月21日收到;2016年11月21日收到修改稿)

基于变分模态分解-相干分析的肌间耦合特性∗

杜义浩1)齐文靖1)邹策1)张晋铭1)谢博多2)谢平1)†

1)(燕山大学电气工程学院,河北省测试计量技术及仪器重点实验室,秦皇岛 066004)

2)(中国人民解放军第281医院康复医学科,秦皇岛 066100)

(2016年7月21日收到;2016年11月21日收到修改稿)

肌间耦合是肢体运动过程中不同肌肉间的相互关联与相互协调作用.通过研究肌电信号(sEMG)间特征频段的耦合特性可以获得肌肉间的功能联系及中枢神经系统支配肢体运动的执行与协调方式机理.本文将变分模态分解与相干分析相结合,构建变分模态分解-相干分析模型,定量描述肢体运动中相关肌肉sEMG在特征频段的耦合特性.在20%最大自主收缩力静态负荷强度下,采集20名健康被试的sEMG,基于变分模态分解方法将sEMG时频尺度化,进而分析不同sEMG在特征频段的相干性,并计算显著相干面积指标,定量分析肌间特征频段的功能耦合特性.结果表明:低负荷静态握力维持过程中,指浅屈肌与尺侧腕曲肌、指浅屈肌与指伸肌的beta与gamma频段耦合强度随时间推进而增强;相较于指浅屈肌与指伸肌,疲劳状态下指浅屈肌与尺侧腕曲肌beta与gamma频段耦合强度变化更显著,且瞬时频率特征变化相似,揭示运动致疲劳过程中协同肌受中枢神经系统控制以更加同步的方式活动.

肌电信号,变分模态分解,相干分析,肌间耦合

1 引 言

人体运动过程中通过神经振荡来传递运动控制信息[1].在中枢神经系统功能调节和反馈控制作用下[2],运动肌肉单元的振荡耦合反映了运动响应信息,肌肉间不同时空层次的耦合现象体现了运动中肌肉间的相互作用与中枢神经对肌肉的支配能力[3].因此,研究运动过程中肌电信号(surface electromyogram,sEMG)间不同时频尺度下的耦合特性,有助于理解肌间耦合作用和中枢神经对肌肉的功能调节与整合机理.

近年来,利用肌间相干分析(intermuscular coherence,IMC)研究运动过程中肌肉间的耦合特性,挖掘潜在的中枢神经运动控制机制的研究相继展开.利用一致性分析方法计算两肌电信号的互谱密度对自谱密度函数的归一化,以反映肌电信号在频域内的耦合关系[4].研究表明,肌间耦合存在频段显著特征,运动过程中肌间耦合主要表现在beta(15—30Hz)频段和gamma(30—45Hz)频段, beta频段的肌间耦合代表了从初级运动皮层到运动神经元的信息传递过程[3],而gamma频段振荡体现与认知功能相关的脑皮层信息整合过程[5].因此,研究特征频段的肌间耦合特性及其变化规律,将有助于探索中枢神经系统的运动控制机制,理解肢体运动控制过程中的组织与协调机理.但是,现有一致性方法只能反映频域下的相干性,无法提取sEMG不同时频尺度下的特征信息,且无法针对某些特征频段进行独立耦合分析.

为此,有研究将小波与相干分析结合,分析肌电信号在不同时频尺度下的耦合特征,并发现不同运动模式及疲劳状态下beta频段耦合特征存在差异[6].然而,由于小波基的约束,导致小波变换缺乏一定的自适应性.近年来,有研究利用经验模态分解(empiricalmode decomposition,EMD)[7]自适应提取sEMG信号不同时频尺度下的特征信息,但该方法存在边界效应及模态混叠现象.而集总经验模态分解(ensemb le em piricalm ode decom position,EEMD)[8]方法能有效地消除模态混叠现象,且具有更好的抗噪性能,但其计算量较大、频谱剖分效果不理想.因此,本文引入变分模态分解(variationalmode decom position,VMD)方法[9,10]分析sEMG信号,将肢体sEMG自适应分解,提取信号中多个具有中心频率的窄带分量,即有限个本征模函数(intrinsic m ode function,IMF),各IMF分量包含了原始sEMG不同时频尺度上的局部特征,同时解决了模态混叠、频谱混叠和计算量大的问题.

为研究不同时频尺度下的肌间耦合特征,本文将VMD与IMC方法相结合,构建变分模态分解-相干分析(VMD-IMC)模型,并将该模型用于20%最大自主收缩力(m aximum voluntary contraction, MVC)静态负荷强度下特征频段的肌间耦合特性分析.基于VMD方法对肌电信号进行时频尺度化,然后利用IMC计算特征频段的相干函数值,分析其特征频段的肌间耦合特性规律;同时结合希尔伯特变换(Hilbert transform,HT),提取均方根(root mean square,RMS)与平均瞬时频率(mean instantaneous frequency,M IF)作为单块肌肉特征观测指标.RMS是常见的反映肌电能量变化的指标[11],M IF能有效地跟踪肌肉状态变化引起的频率波动[12].基于上述方法分析单块肌肉的能量及瞬时频率特征对肌间耦合特性的影响,为研究运动过程中不同肌肉间的耦合特征及中枢神经系统的运动控制机制提供新方法.

2 sEMG信号采集及数据处理

2.1 研究对象与实验流程

采集20名健康被试(男生14名,女生6名;年龄为(25±3)岁)20%MVC静态负荷状态下的上肢sEMG.要求被试实验前无肌肉疲劳现象、精神状态良好,且熟悉实验流程.利用美国Delsys公司TrignoTMW ireless EMG采集设备,分辨率设为16 bit,采样频率为2000 Hz;分别记录被试右臂指浅屈肌(fl exor digitorum superficialis,FDS)、指伸肌(extensor digitorum,ED)、尺侧腕屈肌(flexor carpi ulnaris,FCU)的sEMG,放置电极前用75%酒精擦拭皮肤,如图1(a)所示.实验过程如下:实验前,被试静坐使上臂自然下垂,腕部用绷带固定在支架上,以保持实验过程中姿势不变,调节支架使前臂与地面平行,上臂与前臂约呈90◦夹角;测量被试MVC,重复3次取均值;实验开始,要求被试手持握力传感器发力达到20%MVC,通过显示器的视觉反馈来维持握力恒定(图1(b)),直至被试肌肉疲劳无法维持20%MVC,停止实验.由于个体差异性,实验持续时间不等,实验持续时间(104.6±37.5)s.

图1 被试sEMG采集实验 (a)采集设备与电极位置;(b)握力反馈界面Fig.1.sEMG signal acquisition experim ent of one sub ject:(a)sEMG acquisition equipm ent and the position of electrodes;(b)the feedback interface of grip strength.

2.2 sEM G数据预处理

为了获取更为有效的sEMG特征为进一步的耦合分析做准备,对20名被试上肢sEMG数据进行预处理,利用FIR数字滤波器对肌电信号进行带通滤波,去除50 Hz工频和谐波,降低低频信号能量,使得sEMG主要集中在5—200 Hz之间,结果如图2所示.

图2 sEMG预处理 (a)原始sEMG频谱;(b)sEMG预处理后频谱Fig.2.The preprocessing of sEMG:(a)The spectrum of original sEMG;(b)the spectrum of sEMG after p retreatm ent.

3 sEMG肌间耦合分析

为研究特征频段上的肌间耦合特性,构建变分模态分解-相干分析模型应用于肌电信号耦合分析中.首先,利用VMD对sEMG进行尺度化,获得sEMG不同时频尺度上的信息,然后运用相干分析方法,计算特征频段的肌间相干值,并引入显著相干面积指标定量描述sEMG特征频段的功能耦合特征;利用VMD-HT分析运动过程中单块肌肉的瞬时特征变化规律,研究单块肌肉对肌间耦合特性的贡献及影响.

3.1 基于VM D的sEM G时频尺度化

由于sEMG具有非平稳、非线性特点,引入VMD方法将sEMG自适应分解为有限个IMF分量,每一个模态定义为调幅-调频信号,表达式如下:

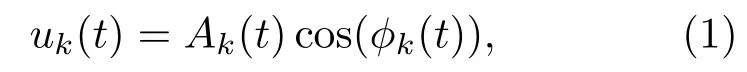
式中,Ak(t)为瞬时幅值,ϕk(t)为相位.

与EMD循环筛选剥离的信号处理方法不同, VMD通过搜寻约束变分模型的最优解,实现信号自适应分解获取IMF分量,每个分量的中心频率和带宽在求解变分模型的迭代过程中不断更新,在满足(2)式的约束条件时,将sEMG信号分解为K个IMF分量.

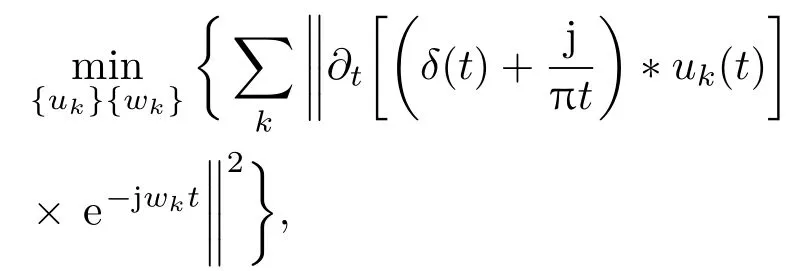
式中,{uk}:={u1,···,uk}代表分解得到的K个有限带宽IMF分量,{wk}:={w1,···,wk}代表各分量的频率中心.引入增广的Lagrange函数求取上述约束性变分模型的最优解,表达式为

式中,α为惩罚参数,λ为Lagrange乘子.

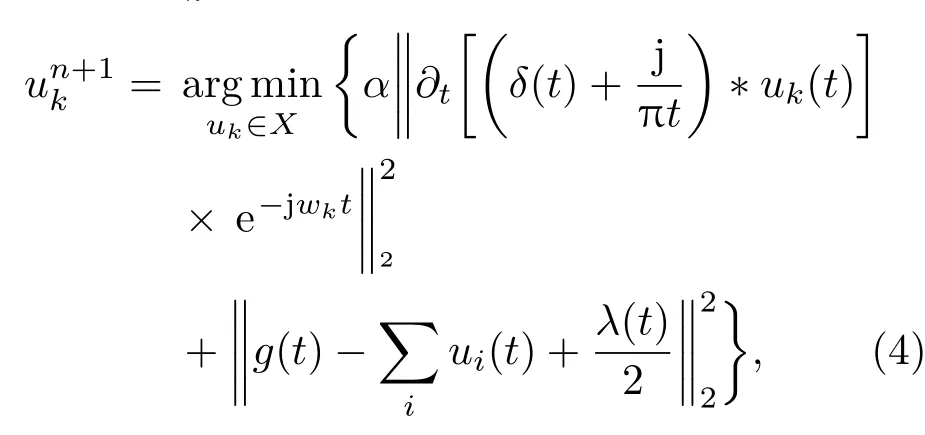
利用Parseval/Plancherel傅里叶等距变换,将(4)式转变到频域,得到各模态的频域更新;然后将中心频率的取值问题转换到频域,得到中心频率的更新方法;同时根据

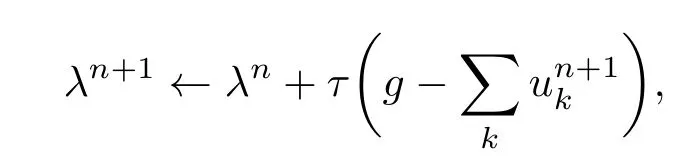
更新λ,此时,二次优化问题的解为

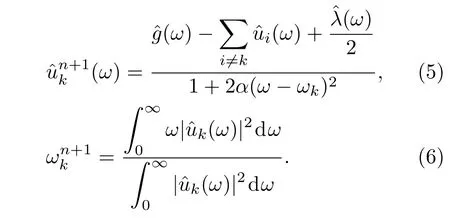
对于给定判别精度b＞0,当满足迭代停止条件

结束整个循环最终根据实际信号的频域特性得到K个窄带IMF分量,完成信号频带的自适应分割,有效地避免了模态混叠.

3.2 基于VM D-IM C的肌间时频耦合分析

首先,运用3.1节中VMD方法得到包含时频尺度信息的IMF分量,然后根据IMF分量的频谱分布进行分频段相干性分析,并计算显著相干面积指标定量刻画肌间的耦合特性,具体如下.

1)令X和Y表示两通道sEMG的频谱能量集中在相同频段的IMF分量,计算其相干函数:

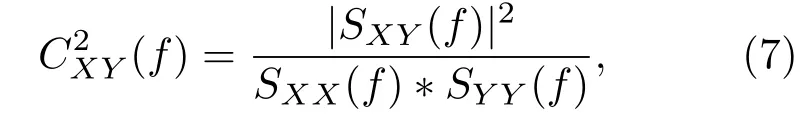
式中,SXY(f)为互谱密度;SXX(f),SYY(f)分别为自谱密度.为改善谱估计器性能,采用滑动平均技术,将数据加窗处理,并计算每一段的相干函数值.

2)为定量描述两信号的相干程度,在sEMG相干函数基础上,引入显著性相干阈值[13]:

式中,n为窗口数,β为置信水平(本文设置为0.95).

进一步利用(9)式计算显著相干面积指标A,即显著相干阈值以上的面积,定量描述sEMG信号间相干性的变化趋势:

式中,Δf为频率分辨率,A的数值越大表示特定频段内的相干性越显著.

3.3 基于VM D-HT的单块肌肉瞬时特征分析

在利用VMD-IMC实现肌间耦合特征提取的基础上,为进一步分析单块肌肉瞬时频率特性对肌间耦合特性的影响,将VMD分解后的sEMG各IMF分量进行HT,并利用RMS和M IF定量描述单块肌肉sEMG的幅值和振荡频率随时间的变化规律,进而分析该瞬时频率特性对肌间耦合变化的影响,具体如下.

对VMD分解后的各IMF分量进行HT得到sEMG的瞬时频率和幅值[12],

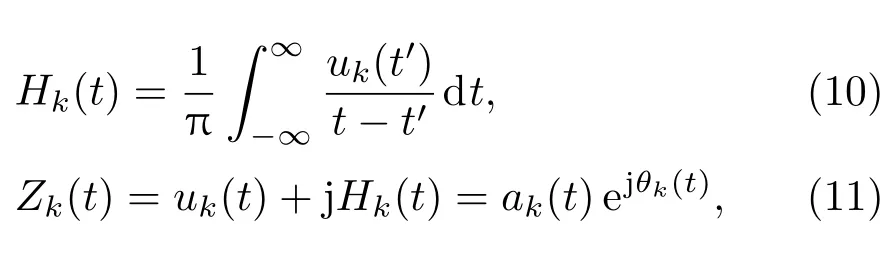
(11)式中Zk(t)的相位表达方式突出了HT的物理意义,它是基于时间序列形成的一个振幅和相位调制的三角函数.则希尔伯特谱的瞬时频率被定义为

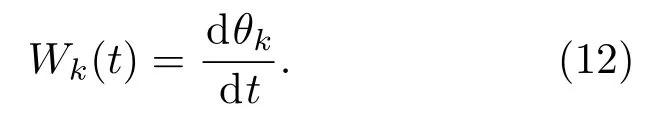
然后,基于sEMG第k个IMF分量uk(t)的幅值ak(t)和瞬时频率Wk(t),计算uk(t)的平均瞬时频率.根据获得的各IMF分量的平均瞬时频率M IFk及幅值,分别计算原始信号的平均瞬时频率和均方根值,如(13)和(14)式所示:

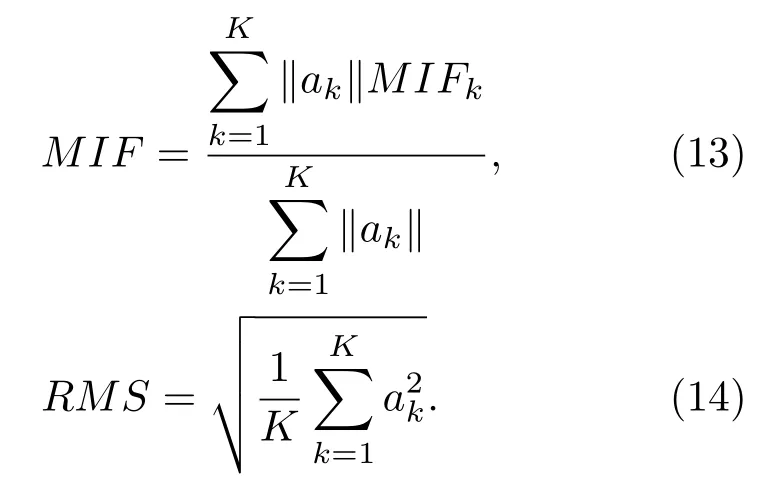
基于上述RMS与M IF指标,分析静态握力输出过程中,肌肉的能量与平均瞬时频率随运动时间变化的规律.

4 实验结果与讨论

sEMG不同频段内的耦合特性反映中枢神经系统的支配信息[14],运动过程中肌间耦合突出表现在beta(15—30 Hz)频段与gamma(30—45 Hz)频段,且beta与gamma的耦合强度与中枢神经系统的控制有关[15,16].本文基于VMD-IMC方法对静态握力维持过程中beta与gamm a频段耦合特性进行分析,并结合HT分析被试运动过程中单块肌肉瞬时特征与肌间耦合特性的联系.

4.1 基于VM D-IM C的上肢sEM G耦合分析

按照2.1节中的实验过程采集每位被试右臂的FDS,FCU和ED的sEMG,对预处理后的sEMG运用FIR滤波器进行0—70 Hz带通滤波,并以20 s为时间间隔对每位被试采集的3通道sEMG进行分段处理.

利用VMD方法将信号分解成若干个窄带IMF分量,提取sEMG不同时频尺度信息.与EMD的递归式模态分解不同,VMD将模态的估计转变为变分问题求解,避免了因估计误差在递归过程中被放大而导致的模态混叠问题.图3为被试sEMG分别经EMD,VMD分解后的结果及各IMF分量的频谱分布,对比图3(a)和图3(b)可见, EMD分解后得到的各IMF间存在明显的频谱混叠问题,也说明相近的特征时间尺度分布在不同的IMF中即模态混叠.而VMD方法很好地实现了频带分离,有效地避免了模态混叠,降低了相邻频段对特征频段耦合的影响.

进一步,运用3.2节所述方法将VMD分解与相干性分析相结合,根据IMF分量频谱分布情况(见表1),选择频谱能量集中分布在beta和gamma频段的IMF,分别对每一段(时长20 s)的FDSFCU与FDS-ED进行beta和gamm a独立频段肌间相干分析,提取显著相干面积指标.根据各段耦合强度分析beta与gamma频段耦合随时间的变化规律,图4为随机选取被试9、被试13(其他被试的结果与此相似)FDS-FCU与FDS-ED的beta和gamma频段肌间耦合强度随时间的变化.分析图4发现:1)FDS-FCU与FDS-ED在beta与gamma频段的显著相干面积随运动时间呈上升趋势;2)曲线终止点显著相干面积值比起始点高,分析可能主要受疲劳因素影响,为此进一步比较疲劳与非疲劳状态耦合特征,计算实验开始后20 s与实验结束前20 s的两组肌肉sEMG在beta和gamma频段肌间相干函数值.为了便于描述,将实验开始后20 s数据与实验结束前20 s数据分别记为实验开始段与实验结束段.

图5为随机选取的被试2与被试8实验开始段和实验结束段beta与gamma频段的独立相干结果.由图5可见:1)相比于实验开始段,实验结束段FDS与ED,FDS与FCU的beta与gamma频段耦合增强;2)对比FDS与ED,FDS与FCU的耦合强度变化更明显.为了分析上述现象是否具有普遍性,并定量地描述特征频段IMC的差异,利用3.2节方法提取20名被试实验开始段与实验结束段在beta与gamma频段的FDS与FCU,FDS与ED显著相干面积指标,并计算其均值与方差,对两个频段各组相干面积值进行独立样本T检验,结果如图6所示.分析图6发现:对比实验开始段与实验结束段,FDS与FCU的beta和gamm a频段的显著相干面积指标具有显著差异(p＜0.05),图6中*表示具有显著差异.

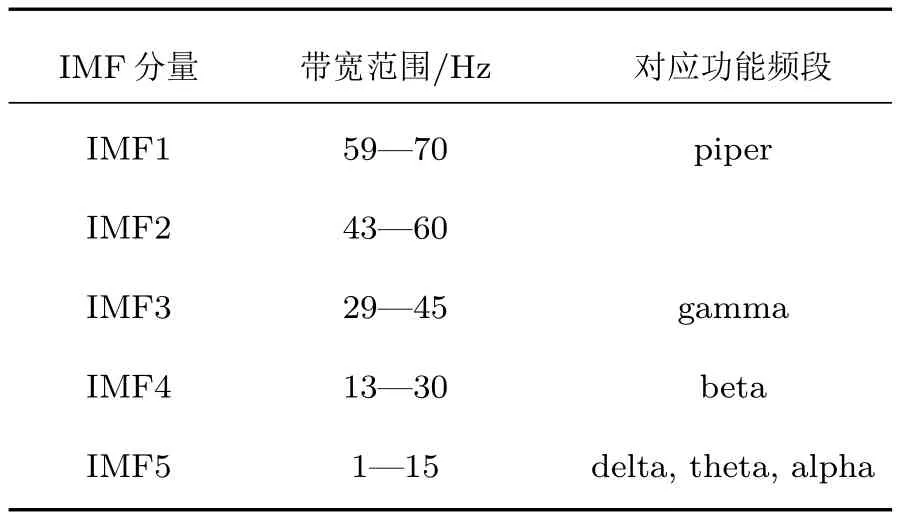
表1 被试0—70 Hz表面肌电信号VM D分解后各分量的带宽及其所对应的功能频段Tab le 1.The frequency range and the correspond ing function spectrum of each com ponent in 0–70 Hz surface EMG after VMD decom position.

sEMG不同频段的耦合特征能够反映神经肌肉系统调控的相关信息[14],其相干函数值反映运动皮层与脊髓运动中枢对运动肌肉的同步支配水平[16,17].本文发现低负荷静态力下FDS与FCU,FDS与ED在beta与gamma频段的耦合随着运动时间的延长呈上升趋势,而Danna-Dos Santos等[18]也发现静态负荷手部大部分肌肉sEMG相干性在0—35 Hz频段内随运动时间增强.随着运动时间的累加,运动相关肌肉的生理状态会发生改变并逐渐呈现疲劳状态,为了维持运动的稳定,中枢神经系统会调节相关肌肉的支配方式,增加对肢体的控制强度,使得静态低负荷运动下的肌肉疲劳过程中皮层神经元与运动神经元池之间的同步耦合增强[14].

图4 被试9、被试13 beta与gamm a频段显著相干面积随时间变化曲线 (a)FDS与FCU;(b)FDS与EDFig.4.The curves abou t signifi cant coherent area of beta and gamm a band of the sub ject 9 and the sub ject 13:(a)FDS and FCU;(b)FDS and ED.

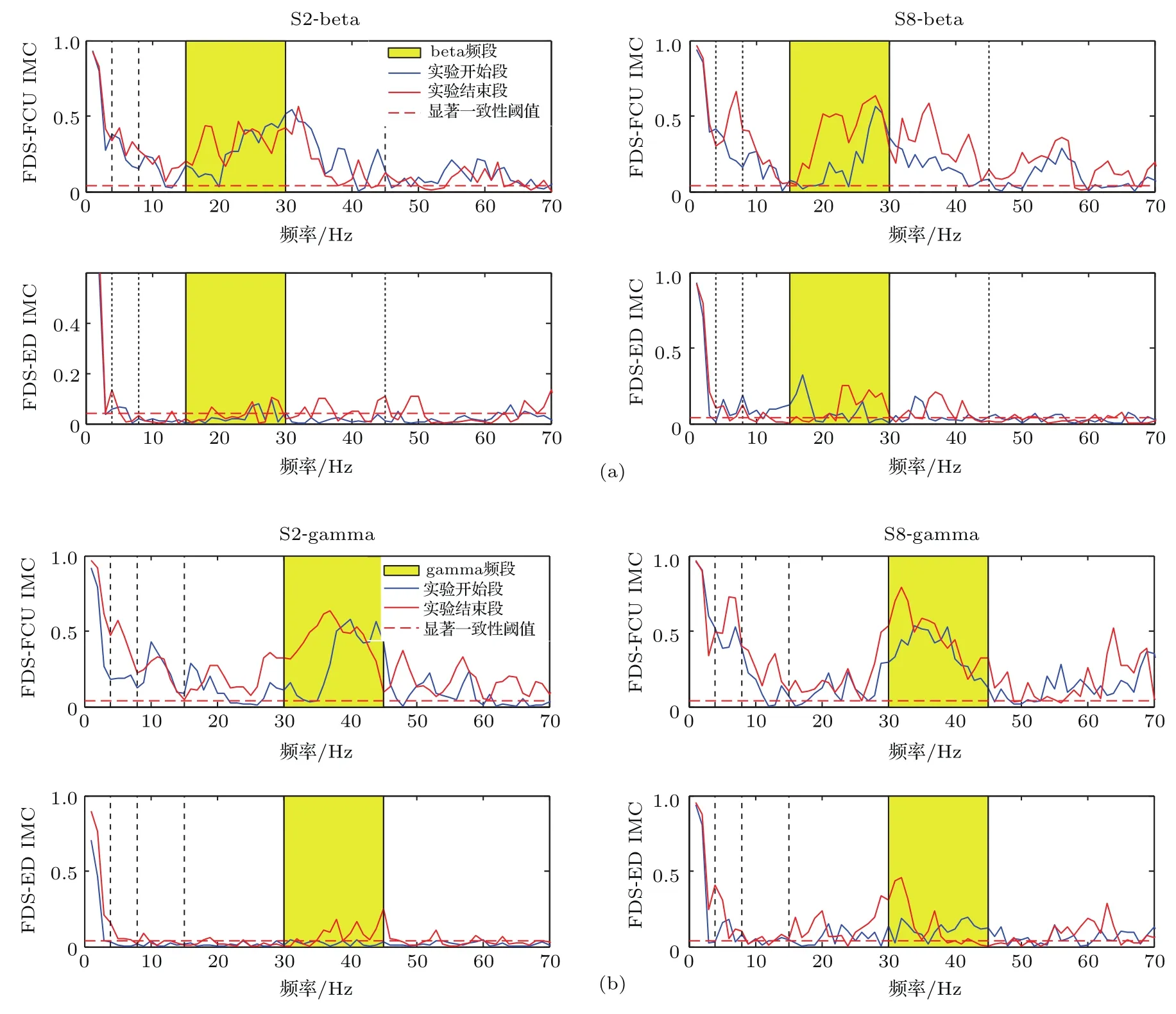
图5 实验开始段与实验结束段的IM C对比 (a)beta频段IMC对比;(b)gamm a频段IMC对比Fig.5.Com parison of IM C between the start period of experim ent and the end period of experim ent: (a)Com parison of IMC in beta band;(b)com parison of IMC in gamm a band.

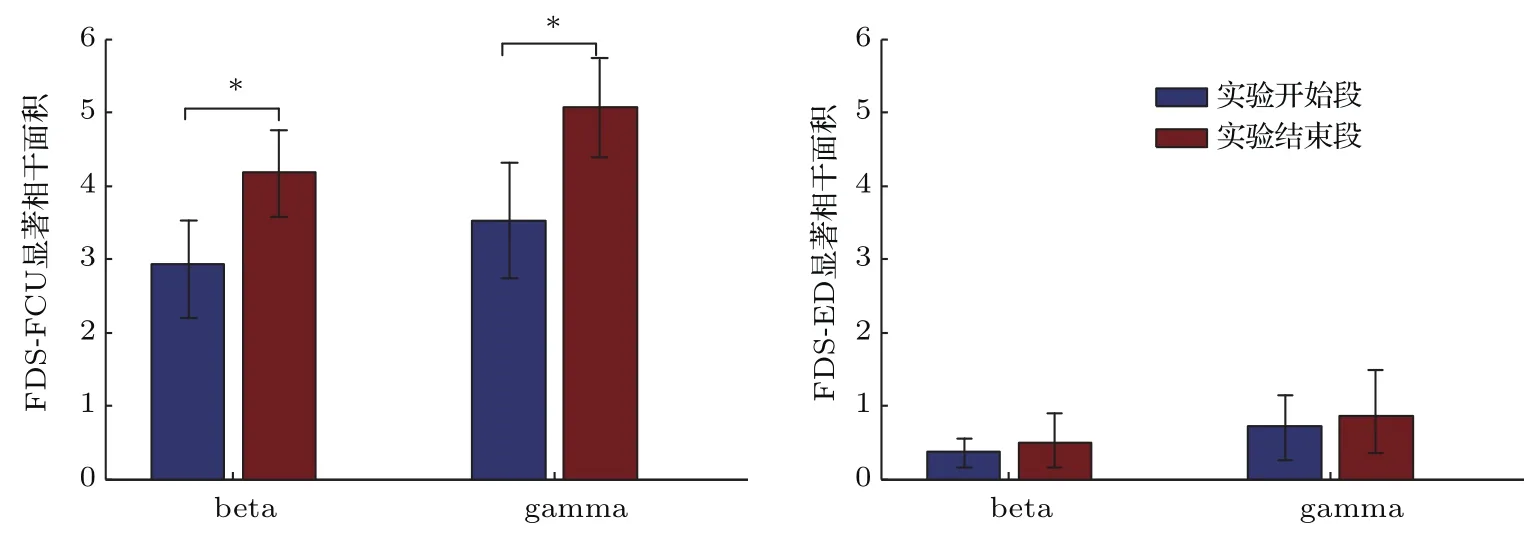
图6 20名被试实验开始段与实验结束段的beta和gamma频段显著相干面积的均值与方差(*代表p＜0.05)Fig.6.Themeanandvarianceofsignificantcoherentareaofthebetaandgammabandinthestartperiod andtheendperiodofexperimentfrom20subjects(*showsp＜0.05).

分析疲劳因素对肌间耦合的影响,对比实验开始段与实验结束段的beta与gamma频段的耦合强度,FDS与FCU的耦合比FDS与ED的耦合变化显著,这与Kattla和Lowery[14]的研究结果相似.FDS与FCU作为运动的协同肌,FDS与ED作为运动的拮抗肌,两组肌肉的神经控制运动机制是不同的[19,20].所以上述协同肌肉与拮抗肌的耦合差异,可能主要由于中枢神经系统对疲劳状态下的两组肌肉采取不同的控制方式.

4.2 基于VMD-HT的sEMG瞬时特征分析

为进一步分析被试运动过程中单块肌肉对肌间耦合特性的贡献及影响规律,运用VMD-HT方法定量分析单块肌肉的瞬时特征.图7和图8分别为20名被试上肢维持20%MVC状态下3块肌肉sEMG的RMS与MIF指标的均值及方差随运动时间的变化.图7和图8横轴表示运动时间,根据被试静态力维持的运动时间截取实验数据,即将被试总的实验数据平均分为10段,计算每一段的RMS和MIF值.由图7可见,FDS,FCU,ED的sEMG的RMS值随运动持续时间表现出递增趋势,表明随着运动时间的延长,运动相关肌肉需要更多的能量来维持运动.分析图8可见,3块肌肉的MIF值随运动持续时间呈递减趋势,其中ED的MIF值下降并不显著,而且集中分布在高频区.

20%MVC静态握力维持过程中,FDS与FCU表现出负荷运动中肌肉产生运动性疲劳的典型特征[21],即MIF指标随运动持续时间表现出明显下降趋势.而指伸肌的MIF变化并不明显,并且ED在实验前后也并未表现出显著的运动性肌肉疲劳.结合肌间耦合特性与单块肌肉的瞬时特征进行分析发现,相比于ED,FCU与FDS的sEMG瞬时频率变化规律更一致,这可能是FDS与FCU耦合比FDS与ED耦合显著的原因,进一步说明了疲劳状态下中枢神经系统对协同肌与拮抗肌采取不同的调控方式,大脑控制协同肌以更加同步的方式活动[22].

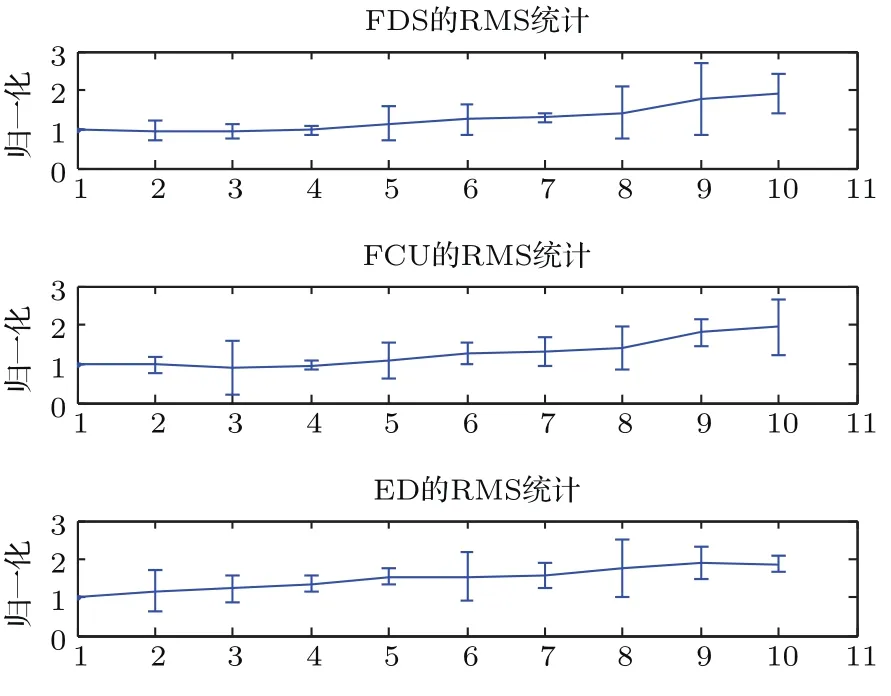
图7 20%MVC下sEMG的RMS随运动持续时间变化特征示意图Fig.7.ThevarianceofRMSunder20%maximum gripstrength.

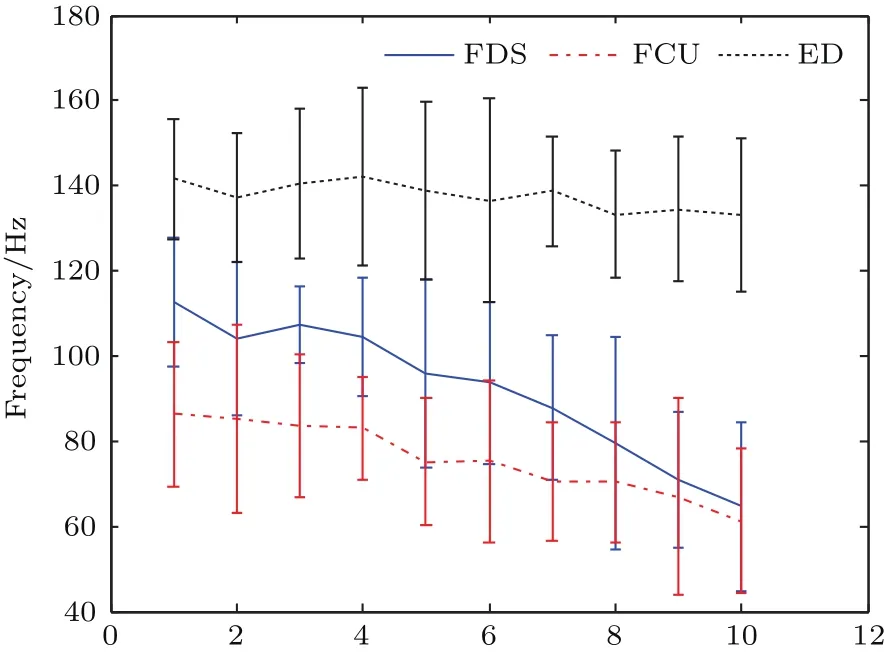
图8 20%MVCsEMG的MIF随运动持续时间变化特征示意图Fig.8.ThevarianceofMIFunder20%maximumgrip strength.

5 结 论

本文将VMD方法引入到肌间耦合分析中,并与IMC方法相结合,建立了VMD-IMC肌间耦合分析模型,应用于健康人20%MVC静态负荷强度握力输出条件下的sEMG同步耦合特性分析.结果表明:低负荷静态握力维持过程中,FDS与FCU, FDS与ED的beta与gamma频段耦合强度随运动时间呈增强趋势,且疲劳状态下FDS与FCU间耦合变化更显著;分析单块肌肉瞬时频率特征发现,相比于ED,FCU与FDS的瞬时频率特征变化更一致.中枢神经系统对运动过程中的协同肌与拮抗肌采取了不同的调节支配方式,并控制协同肌以更加同步的方式活动.因此,本文提出的变分模态分解-相干分析方法可以刻画肌电信号在不同时频尺度上的特征,是特征频段肌间耦合特性分析的有效方法,为探索运动功能控制机制及运动功能障碍产生机理提供方法.

[1]Baker S N 2007 Curr.Opin.Neurobiol.17 649

[2]Enoka R M,Baud ry S,Rudroff T 2011 J.Electrom yogr. K ines.21 208

[3]G rosse P,Cassidy M J,B rown P 2002 C lin.Neurophysiol.113 1523

[4]X ie P,Song Y,Guo Z H,Chen X L,W u X G,Su Y P, Du Y H 2016 J.Biom ed.Eng.33 244(in Chinese)[谢平,宋妍,郭子晖,陈晓玲,吴晓光,苏玉萍,杜义浩2016生物医学工程学杂志33 244]

[5]Patino L,Om lor W,Chakarov V 2008 J.Neurophysiol. 99 1906

[6]Charissou C,V igouroux L,Berton E 2016 J.Electrom yogr.Kines.27 52

[7]Stam ou lis C,Chang B S 2011 33rd Annual In ternational Conference of the IEEE EMBS Boston,USA,August 30–Sep tem ber 3,2011 p5908

[8]W u Z,Huang N E 2009 Adv.Adapt.Data Ana ly.1 1

[9]D ragom iretskiy K,Zosso D 2014 IEEE Trans.Signal Process.62 531

[10]X ie P,Yang F M,Li X X,Yang Y,Chen X L,Zhang L T 2016 Acta Phys.Sin.65 118701(in Chinese)[谢平,杨芳梅,李欣欣,杨勇,陈晓玲,张利泰2016物理学报65 118701]

[11]Lattim er L J,Lanovaz J L,Farthing J P 2016 J.E lectrom yogr.Kines.30 231

[12]X ie H,W ang Z 2006 Com put.M eth.Prog.Biol.82 114

[13]Rosenberg J R,Am jad A M,B reeze P 1989 Prog.Biophys.M ol.Bio l.53 1

[14]K attla S,Lowery M M 2010 Exp.Brain Res.202 89

[15]Om lorW,Patino L,Hepp-Reym ond M C 2007 Neuroimage 34 1191

[16]Baker S N,O livier E,Lem on R N 1997 J.Physiol.501 225

[17]Salenius S,Portin K,Kajola M 1997 J.Neurophysiol. 77 3401

[18]Danna-Dos Santos A,Poston B,Jesunathadas M 2010 J.Neurophysio l.104 3576

[19]Gandevia S C 2001 Physio l.Rev.81 1725

[20]W ang L J,Lu A Y,Zheng F H,Gong M X,Zhang L, Dong F 2014 China Sport Sci.34 40(in Chinese)[王乐军,陆爱云,郑樊慧,龚铭新,张磊,董菲2014体育科学34 40]

[21]de Luca C J 1997 J.Appl.Biom ech.13 135

[22]Lévénez M,Garland S J,K lass M 2008 J.Neurophysiol. 99 554

PACS:87.85.Ng,05.45.–aDOI:10.7498/aps.66.068701

Interm uscu lar coup ling characteristics based on variationalm ode decom position-coherence∗

Du Yi-Hao1)QiWen-Jing1)Zou Ce1)Zhang Jin-M ing1)Xie Bo-Duo2)Xie Ping1)†

1)(K ey Laboratory ofM easurem ent Technology and Instrum entation of Hebei Province,Institute of Electric Engineering, Yanshan University,Qinhuangdao 066004,China)
2)(Departm ent ofRehabilitation M edicine,the No.281 Hospital ofChinese Peop le’s Liberation Arm y, Q inhuangdao 066100,China)
(Received 21 Ju ly 2016;revised m anuscrip t received 21 Novem ber 2016)

Intermuscular coup ling is defined as the interaction,correlation and coordination between diff erentmuscles during the body movement,which could be revealed by the synchronization analysis of surface electromyogram(sEMG).The multiscaled coherence analysis of sEMG signals could describe themultip le spatial and tem poral functional connection characteristics of intermuscular coup ling,which cou ld be help fu l for understanding the multip le spatial and tem poral coup ling m echanism of neuromuscular system.Furtherm ore,the coup ling characteristics in frequency band of sEMG generally refl ect the functional connection between muscles which relate to m otion control and coordinativem echanism of the central nervous system(CNS).

In this paper,we combine variational m ode decom position(VMD)and intermuscu lar coherence(IMC)analysis to propose a new m ethod nam ed VMD-IMC to quantitatively describe the muscular coup ling characteristics in the corresponding frequency bands.First,sEMG data of flexor digitorum superfi cialis(FDS),flexor carpi u lnaris(FCU) and extensor digitorum(ED)are recorded simu ltaneously from twenty healthy sub jects(25±3 years)who perform the designed grip task at sustained 20%m aximum voluntary contraction under the static load.Then,the VMD approach is em p loyed to adaptively decom pose sEMG into several intrinsic mode functions to describe the information about diff erent tim e-frequency scales.Furtherm ore,the coherence on diff erent tim e-frequency scales between diff erent sEMG signals is analyzed,and the signifi cant coherent area index is calculated to quantitatively describe the functional coup ling characteristics of the feature bands.And combining VMD w ith Hilbert transform,we calculate root m ean square and m ean instantaneous frequency(M IF)to describe the variations of energy and frequency of each muscle.The results show that coup ling strengths increase w ith time,respectively,in beta(15–30 Hz)and gamma(30–45 Hz)band between two muscles(FDS vs FCU,FDS vs ED)during the sustained static force w ith low load.In addition,com pared w ith the coup ling between FDS and ED,the coup lings between FDS and FCU in beta and gamm a band under the condition of fatigue present more significant changes and sim ilar trend in M IF variation w ith time.The obtained results reveal that the congenerousmuscle is coordinated by CNS in am ore synchronousway during the sustained isom etric fatiguing contraction.

electromyogram,variationalmode decom position,coherence,intermuscular coup ling

10.7498/aps.66.068701

∗国家自然科学基金(批准号:61271142)、河北省自然科学基金(批准号:F2015203372,F2014203246)和河北省高等学校科学技术研究项目(批准号:QN 2016094)资助的课题.

†通信作者.E-m ail:p ingx@ysu.edu.cn

*Pro ject supported by the National Natu ral Science Foundation of China(G rant No.61271142),the Natu ral Science Foundation of Hebei Province,China(G rant Nos.F2015203372,F2014203246),and the Science and Technology Research Pro ject of Higher Education Institutions in Hebei Province,China(G rant No.QN 2016094).

†Corresponding author.E-m ail:pingx@ysu.edu.cn