用于透明平板平行度和均匀性测量的单元件干涉仪∗

兰斌 冯国英†张涛 梁井川 周寿桓2)

1)(四川大学电子信息学院激光微纳工程研究所,成都 610064)

2)(华北光电技术研究所,北京 100015)

(2016年11月10日收到;2016年11月29日收到修改稿)

用于透明平板平行度和均匀性测量的单元件干涉仪∗

兰斌1)冯国英1)†张涛1)梁井川1)周寿桓1)2)

1)(四川大学电子信息学院激光微纳工程研究所,成都 610064)

2)(华北光电技术研究所,北京 100015)

(2016年11月10日收到;2016年11月29日收到修改稿)

提出了一种基于单元件干涉的用于检测透明介质平整度和均匀性的干涉仪.该干涉仪的核心元件是一个菱形分光棱镜.激光光源的平面波光束的一半光束透过待测样品,另一半光束直接透过空气,然后分别入射到菱形分光棱镜的两垂直面并在分光面相遇、相干.通过旋转待测样品改变相干的两束光光程差,从而使干涉条纹发生移动.形成的相干光被分光板分成两束,一束进入光电探测器用于探测干涉条纹移动数的整数部分,另一束则进入电荷耦合探测器用于采集干涉条纹图来计算干涉条纹移动数的小数部分.通过计算条纹移动数反推出光程差的变化量,再结合折射率或样品厚度信息则可以计算出样品厚度或折射率的分布,从而检测出透明介质的平行度和均匀性.模拟仿真和光学实验均证明了本方法的可行性、准确性和稳定性.

干涉测量法,相位测量,图像处理,折射率

1 引 言

激光干涉测量法具有非接触、高精度、高效率等优点,通过设计不同的干涉仪装置,可以用于测量样品的表面形貌[1−3]、折射率[4−6]、厚度[7,8]和振动过程[9,10]等参数,因此被广泛应用于工业自动化加工和产品在线检测等领域.

透明平板(如有机玻璃、塑料板等)在建筑工业、高科技产品以及科研等领域的应用越来越广,其平整度及均匀性的测量在加工和质量控制中变得越来越不可避免.透明平板的平整度和均匀性的测量有多种方式,目前基于光电非接触测量的方法仍然以采用反射光信号的测试方案居多.现有的激光位移传感器一般是电荷耦合器(CCD)相机与激光器放置在样品同侧通过探测平板散射光进行测量,并且装置中器件位置相对固定.而透明平板的散射光极弱,再加上CCD相机位置相对固定所以很难直接测量透明平板的平整度和均匀性分布.基于线结构光的反射式平板玻璃的厚度测量装置测量范围广、效率高,但由于光束宽度和CCD相机图像畸变的限制,测量精度相对不高.基于光三角法的激光三角位移传感器是将激光器发出的光束会聚于被测物体上形成一个微小光斑以模拟接触式测头的探针;光斑的大小将影响传感器的横向分辨力、测量范围和测量精度等参数.另外基于共焦法的透明平板平整度测量方法,测量精度相对较高,但光谱分析对高速测量有一定的限制[7,11].

本文提出了一种基于菱形分光棱镜干涉的用于检测透明介质平整度和均匀性的干涉仪.文中首先介绍了测量装置,并详细分析了菱形分光棱镜干涉的原理以及由旋转产生的光程差计算表达式;其次进行了数值仿真,详细地分析了样品旋转与干涉条纹移动情况,随后分别仿真了均匀折射率样品平整度测量以及厚度为10 mm的折射率非均匀分布样品的实验;最后对一个使用一年且存在一定形变的比色皿的平整度进行了测量.模拟仿真和光学实验均证明本文方法的可行性、准确性和稳定性.

2 原理分析

实验装置如图1所示,激光器发出的激光光束以平行光通过旋转样品台,一半直接通过,另一半透射通过待测样品,分别进入分光棱镜后各自的反射光与另一半的透射光相干.产生的干涉条纹图被分光板分成两束,一束通过透镜放大进入我们自制的光电计数器,当条纹移动时负责记录条纹移动数量;另一束通过衰减片后进入CCD探测器,负责采集生成的干涉条纹图,采集到的干涉图像被从中间分成两部分.通过顺时针或逆时针旋转样品,可以使发生干涉的两束光光程差发生改变,从而使干涉条纹发生移动,通过相位解调算法[12−14]计算出样品旋转过程中干涉图相位移动量就可以知道改变的光程,从而得到样品的参数.整个光路设计简单,清晰明了,测量搭建十分方便.

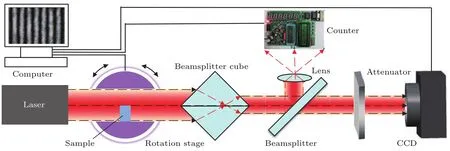
图1 (网刊彩色)实验装置图Fig.1.(color on line)Schem atic of the experim ental setup.

设E1(x′,y′)和E2(x′,y′)分别为入射面上半部分和下半部分入射光的复振幅,且分光棱镜的半反半透膜与z轴间的夹角为α,则出射的透射光平行于入射光,而反射光与透射光间的夹角为2α.从入射光到出射光的过程中将产生相位差,为计算方便将它们分为从分光棱镜出射前的相位漂移φ(α)和从分光棱镜出射后的相位漂移kx·sin(2α)两部分,其中k为波数.并且反射光和透射光之间的相位漂移在出射面上体现在干涉条纹图中.我们采用的分光棱镜分光比为1:1,且通过旋转台前光束为平面波,则上下两部分出射光的光强分别为[15]

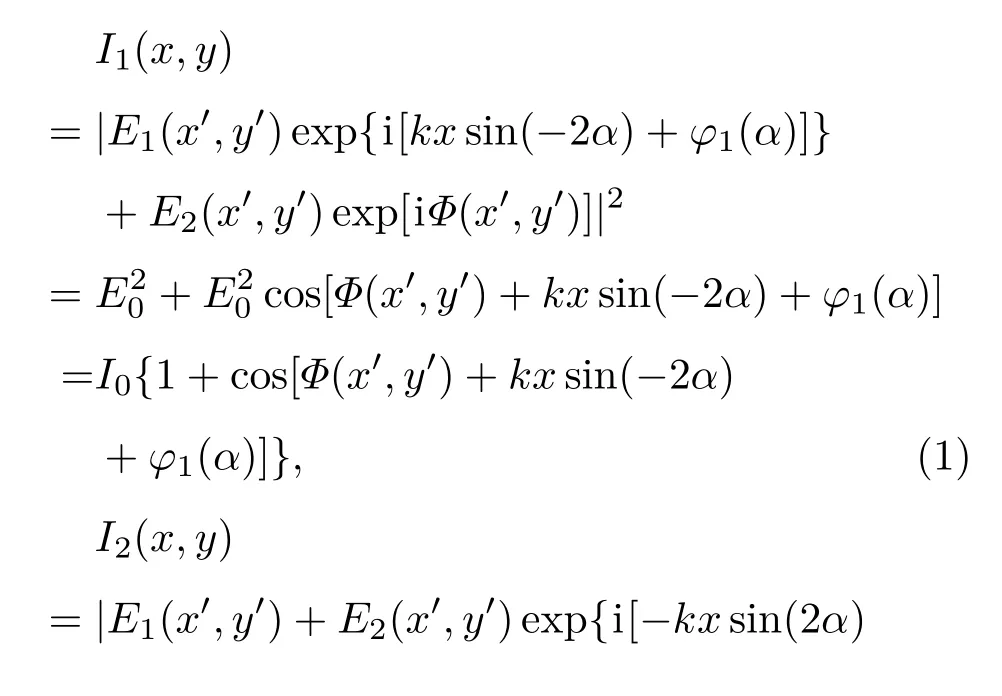
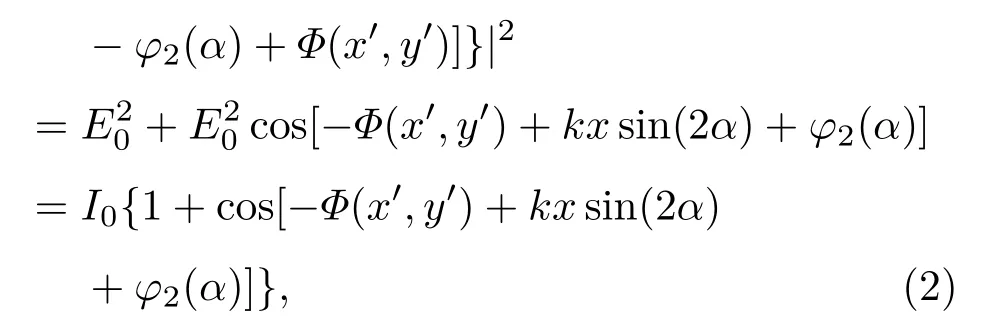
其中Φ(x′,y′)为待测样品引入的相位差.根据分析可知当改变分光棱镜与激光入射方向夹角的角度时,干涉条纹图载频将发生改变,即条纹疏密会发生改变.夹角α越大,干涉条纹越密. CCD采集的干涉条纹图被从中间分成两部分,当旋转样品改变光程差时两部分的条纹移动方向相反,移动数量相同.当Φ(x′,y′)随着样品旋转变为Φ(x′,y′)+Δφ(x′,y′)时,干涉条纹移动数N=Δφ/2π.因此,我们可以通过对旋转样品过程中干涉条纹图的变化情况对样品的平整度和均匀性进行分析.

假设待测样品如图2所示,参考面与测试面间的距离为L,样品的折射率为n,平板的厚度为d, n0是空气的折射率,光线以入射角θ入射,L2和L3分别为光束在空气中传输的距离,L1为光束在样品中传输的距离.

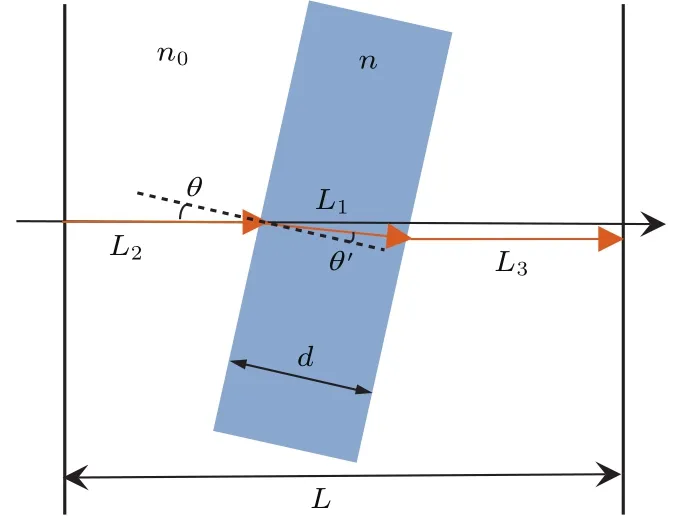
图2 (网刊彩色)测量样品时的光程示意图Fig.2.(color on line)Schem atic diagram of the sam p le op tical path.

根据几何关系,光束通过旋转台后E1(x′,y′)和E2(x′,y′)间的光程差为

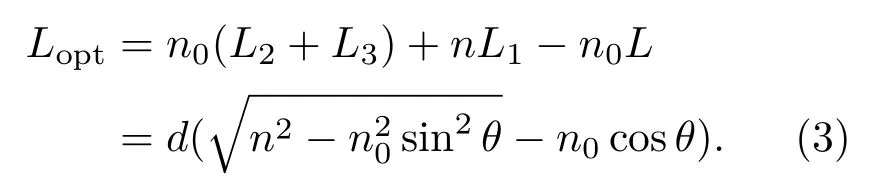
当测量入射角从β变换到θ时,两波面间的相对光程差发生的变化为

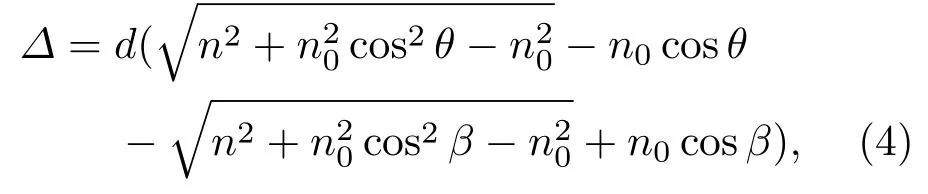
并且根据

求得条纹的移动数N为

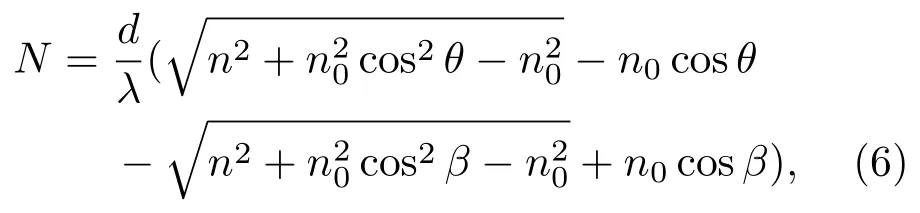
其中λ为激光波长.由此可以得到,当初始测量角度为0,并将空气折射率设置为1时,条纹移动数为[5,6]

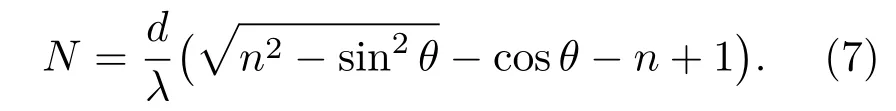
综上分析可知,当系统确定,即光源波长λ一定、旋转台旋转角度一定,则可以根据试验中测得的条纹移动数来估计样品厚度以及折射率分布情况.当待测样品是均匀介质时,装置可以对其厚度分布情况进行准确测量;当样品厚度一定时,装置则可以对样品的折射率分布进行测量,分析其均匀性.

3 数值仿真

为了更详尽地分析整个系统的性能,我们对(7)式进行了深度分析,图3给出了当折射率n=1.3316、样品厚度d=10 mm不变时,像素点灰度(蓝色曲线)和条纹移动数N(绿色曲线)随旋转角度的变化情况,可以看出随着旋转角度增大条纹移动数变大,且条纹移动速度越快,像素点灰度值变化越剧烈.由此可以推断测量时可以通过增大旋转角度来提高测量精度.图4展示了折射率n=1.3316,旋转角度θ=20◦时,像素点灰度(蓝色曲线)和条纹移动数(绿色曲线)随样品厚度的变化情况.可以看出厚度越大时条纹移动数越大,所以可以适当增大待测样品厚度有效提高系统的测量精度.图5给出了厚度d=10mm条件下两种不同折射率(n=1.30和n=1.60)的样品旋转时像素点灰度(蓝色曲线)和条纹移动数N(绿色曲线)的变化情况.可以看出折射率越大的样品旋转时条纹移动数越大,且条纹移动速度更快,像素点灰度值变化越剧烈.由此可以推断,测量折射率更大的样品时在其他条件一致的情况下测量精度更高.

图3 (网刊彩色)设定折射率n=1.3316和样品厚度d=10 mm不变时,像素点灰度(蓝色曲线)和条纹移动数(绿色曲线)随旋转角度的变化Fig.3. (color on line)The gray level(b lue cu rve) and the number of the fringe shifts(green curve) change w ith the rotation angle when the refractive index n=1.3316 and the sam p le thickness d=10 mm.

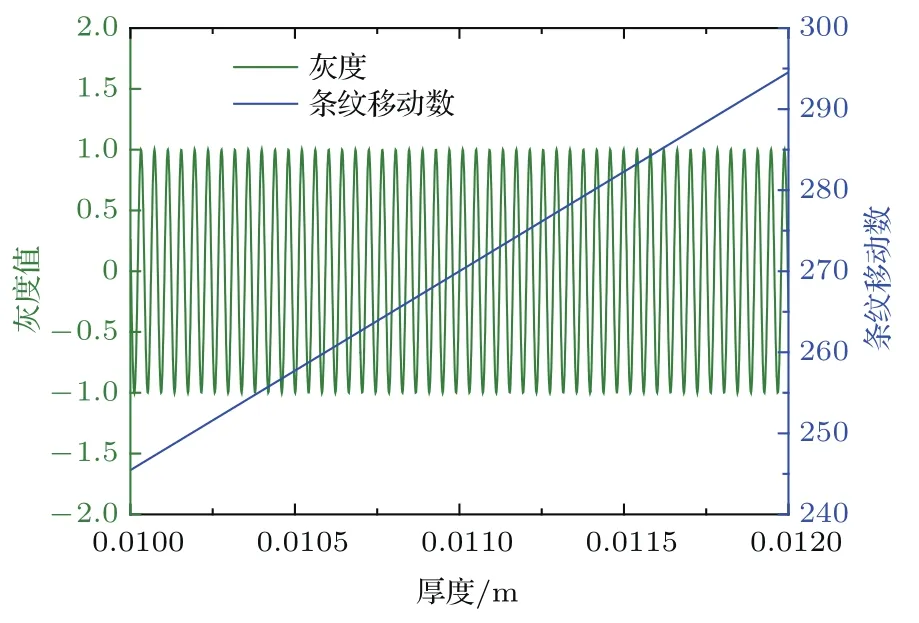
图4 (网刊彩色)设定折射率n=1.3316,旋转角度θ=20◦时,像素点灰度(蓝色曲线)和条纹移动数(绿色曲线)随样品厚度的变化Fig.4.(color on line)The gray level(b lue cu rve)and the num ber of the fringe shifts(green cu rve)change w ith the sam p le thickness w hen the refractive index n=1.3316 and the rotation angleθ=20◦.

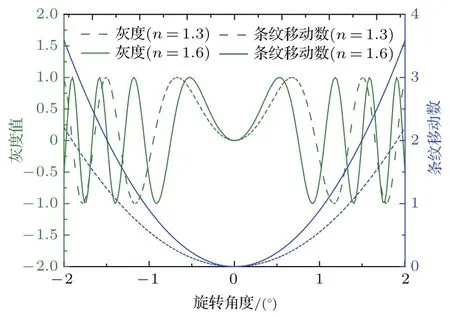
图5 (网刊彩色)设定样品厚度d=10 mm时,对比不同折射率情况下像素点灰度(蓝色曲线)和条纹移动数(绿色曲线)随旋转角度的变化Fig.5.(color on line)The gray level(b lue curves)and the num ber of the fringe shifts(green curves)change w ith the rotation angle for d iff erent refractive index when the sam p le thickness d=10 mm.

可以看出无论是样品折射率还是厚度都会对干涉条纹移动数产生影响,并且将很明显地体现在干涉条纹图上,因此通过测量旋转待测样品过程中干涉条纹移动数是一种很灵敏且高精度的样品平整度和均匀性测量方法.

接下来对实验进行数值仿真,分别对厚度存在略微变化的均匀样品以及厚度不变折射率存在凹凸不平分布的两种样品进行实验仿真.

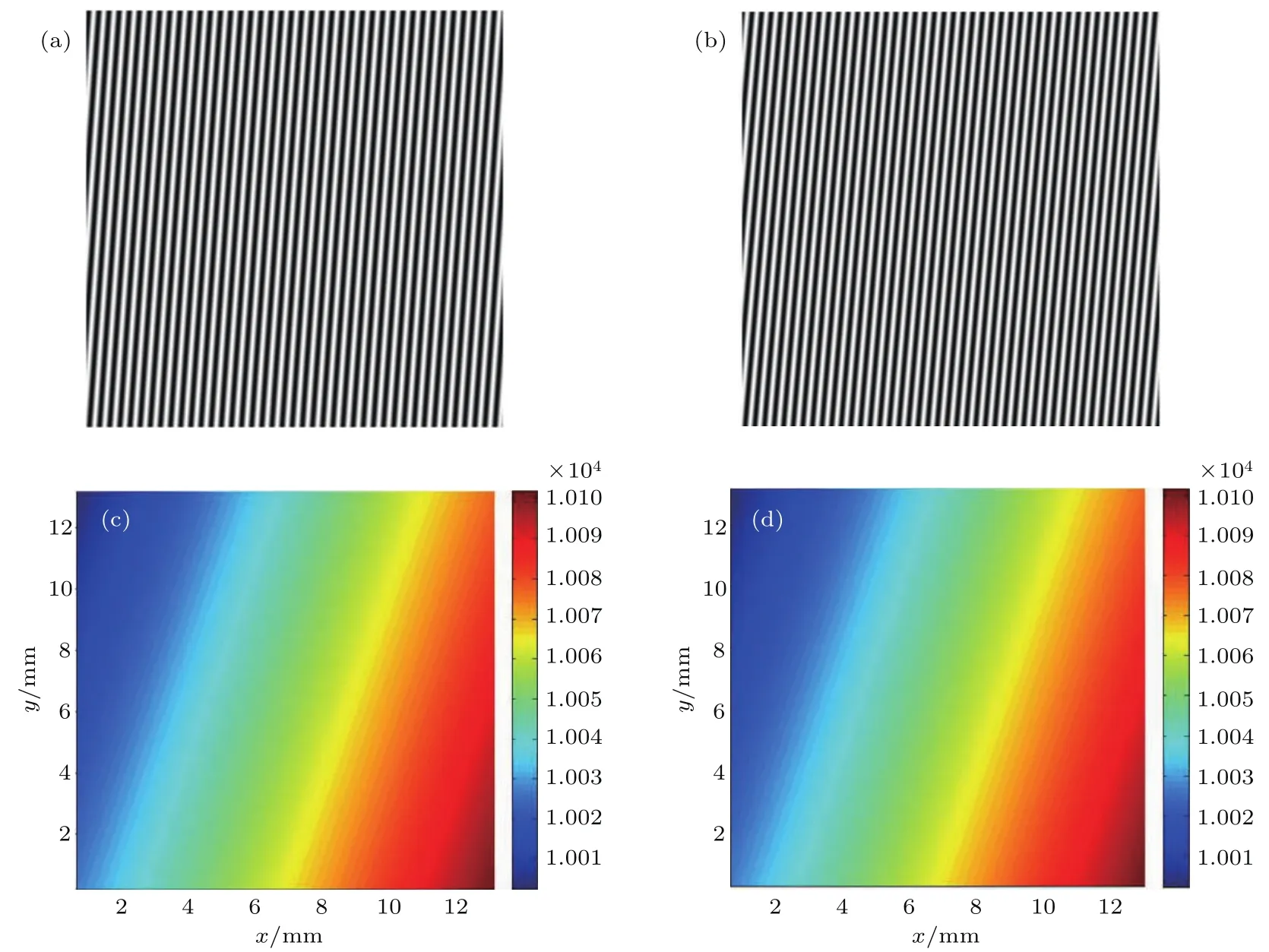
图6 (网刊彩色)均匀折射率样品平整度仿真结果,待测样品在(a)初始位置和(b)旋转20◦后采集的干涉条纹图; (c)仿真的样品厚度分布和(d)根据装置原理仿真计算得到的厚度分布Fig.6.(color on line)The sim u lation resu lts for uniform refractive index sam p le:The interferogram w hen the sam p le at(a)the initial position and(b)rotated by 20◦;(c)the sim u lated sam p le thickness d istribu tion and(d)the calcu lated thickness d istribu tion.

首先,我们模拟了厚度约为10 mm的透明折射率均匀样品.为了与实验装置条件相匹配,仿真中激光光源波长为636.94 nm,空气折射率设置为n0=1,样品为石英玻璃,折射率设置为1.4560,样品旋转角度为20◦,由分光棱镜引入的空间载频为1/8 pixel−1.图6(a)为样品处在原始位置,即入射光束与样品垂直时模拟的CCD相机采集干涉条纹图,图6(b)为仿真的样品旋转20◦后CCD相机采集干涉条纹图.计算可得在样品旋转过程中中心像素点条纹移动数的整数部分为308,在实验中这个数字可以由我们自制的光电计数器探测得到.接下来,通过分析样品旋转前后CCD相机采集的干涉条纹图的相移分布,并将其除以2π即可以得到在此次样品旋转过程中干涉条纹移动数的小数部分分布,最终得到整个样品旋转过程中条纹移动数N.将实验得到的数据与已知条件代入(7)式中即可以得到样品厚度分布如图6(d)所示,图6(c)为仿真中使用的样品厚度分布,图中色标的单位均为微米.图6(c)和图6(d)之差即为测量误差的峰峰值为1.59µm,均方根值为7.46×10−2µm.可见本装置用于测量折射率均匀样品的不平整度是可行的,并且具有很高的精度.

为了在实际试验中校验测量结果,我们对样品的厚度差进行了计算仿真.根据未加样品前仿真得到的干涉条纹图(图7(a))和加入样品后(放置在初始位置)仿真得到的干涉条纹图(图6(a))之间的相位差分布,计算待测样品的厚度差分布,之间的换算关系可由几何光学中光程差和相位差关系式得到.图7(c)所示为仿真样品的厚度差分布,图7(d)为根据干涉条纹图7(a)和图7(b)计算得到的样品厚度差分布.图7(c)和图7(d)之差的峰峰值为0.313µm,均方根值为2.51×10−2µm,图中色标的单位均为µm.可见在没有其他手段对样品进行平整度高精度测量校验本装置测量结果时,可以采用这种自检验的手段对测量结果进行准确性判断.

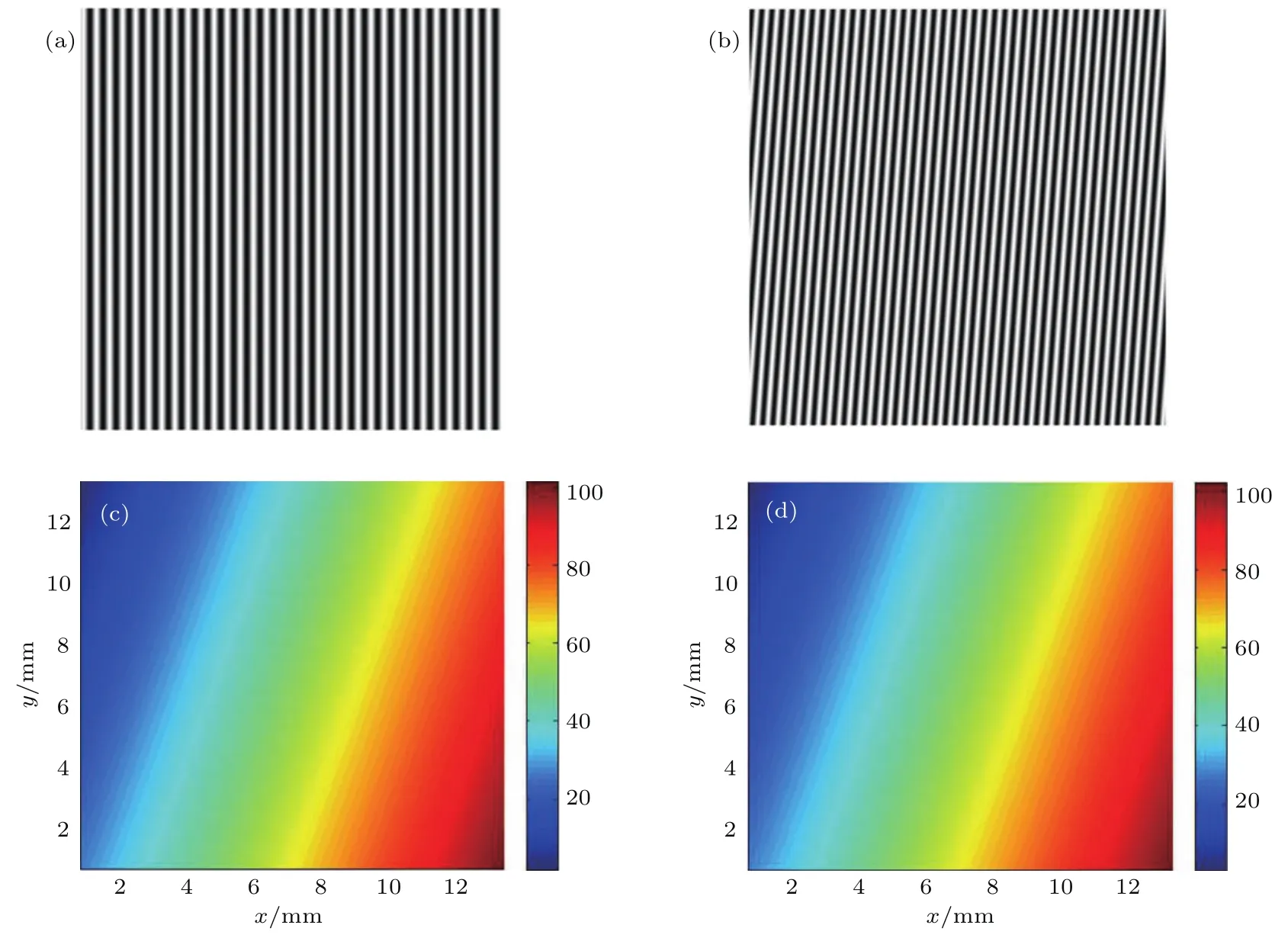
图7 (网刊彩色)均匀折射率样品平整度仿真结果 (a)无待测样品和(b)待测样品在初始位置采集的干涉条纹图; (c)仿真的样品厚度差分布和(d)根据装置原理仿真计算得到的厚度差分布Fig.7.(color on line)The sim u lation resu lts for uniform refractive index sam p le:The interferogram(a)w ithout and(b)w ith sam p le at the initial position;(c)the sam p le thickness d iff erence d istribu tion and(d)the calcu lated thickness d iff erence distribution.

我们模拟了折射率约为1.4560、厚度为10mm的透明样品,其他条件与上一个仿真一致且和我们的实验装置条件相匹配,图8(a)为样品处在原始位置,即入射光束与样品垂直时模拟的CCD相机采集干涉条纹图,图8(b)为仿真的样品旋转20◦后CCD相机采集干涉条纹图.计算可得在样品旋转过程中中心像素点条纹移动数的整数部分为307,在实验中这个数字可以由我们自制的光电计数器探测得到.通过分析样品旋转前后CCD相机采集的干涉条纹图的相移分布,并将其除以2π即可以得到在此次样品旋转过程中干涉条纹移动数的小数部分分布,最终得到整个样品旋转过程中条纹移动数N.将实验得到的数据与已知条件代入(7)式中即可以得到样品折射率分布,如图8(d)所示,图8(c)为仿真中使用的样品折射率分布.图8(c)和图8(d)之差即为测量误差的峰峰值为5.07×10−5,均方根值为5.92×10−6.可见本装置用于测量一定厚度的折射率非均匀分布样品的折射率分布是可行的,并且同样具有很高的精度.

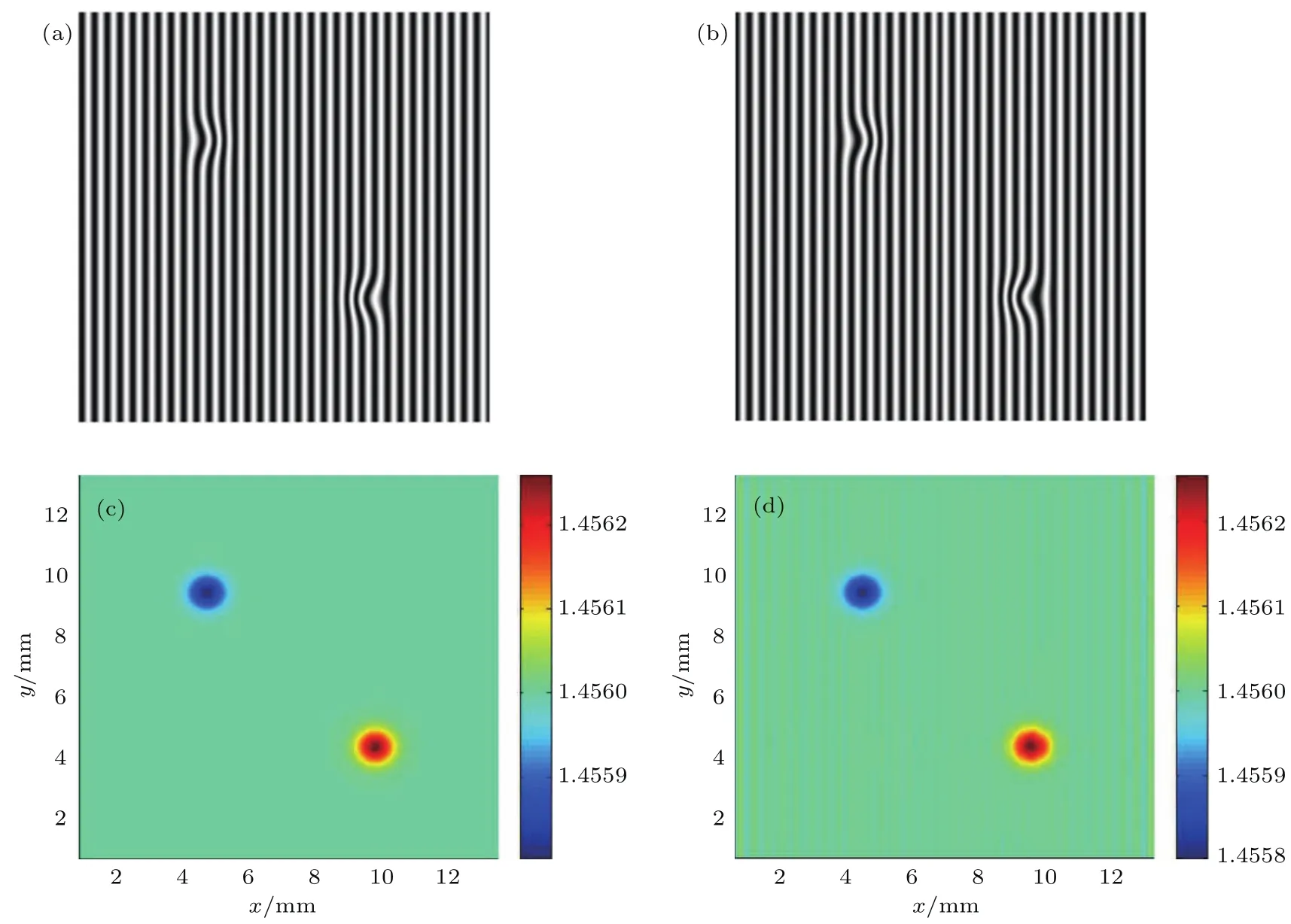
图8 (网刊彩色)厚度为10 mm的折射率非均匀分布样品仿真结果,待测样品在(a)初始位置和(b)旋转20◦后采集的干涉条纹图;(c)仿真的样品折射率分布和(d)根据装置原理仿真计算得到的折射率分布Fig.8.(color online)The refractive index non-uniform distribution of sam p le w ith d=10 mm simu lation resu lts:The interferogram w hen the sam p le at(a)the initial position and(b)rotated by 20◦;(c)the sim u lated sam p le refractive index distribution and(d)the calcu lated refractive index d istribution.

4 实验结果

为了进一步验证本装置在测量中的可行性,我们采用如图9所示的装置对一个使用时间一年、前后表面存在略微倾斜的比色皿进行平整度检测.实验所用激光器为经过准直扩束的半导体激光器,波长为636.94 nm,转动台型号为GCD-011080M,分辨率为2.412′′,待测比色皿厚度约为10 mm,垂直激光传播方向宽度为20 mm并且被从中间隔成相同大小的两部分,隔板放置位置为光束中心,将激光分为相等的两部分,使激光一半透过有水部分,剩余一半透过空气部分,从而产生不同光程.随后这两部分光再进入分光棱镜发生干涉,产生的干涉光再被分光片分成两部分,一部分通过透镜放大进入光电计数器,用于对样品旋转过程中干涉条纹移动数进行计数;另一部分经过衰减后进入CCD相机被记录成干涉条纹图.

图9 (网刊彩色)测量装置实物图,其中,a是激光器光源; b是一半装有二次蒸馏水,另一半为空气的待测比色皿,其放置在转动台上;c是分光棱镜单元件;i是分光片;e是透镜;f是衰减片;g是基于51单片机的自制光电计数器;h是CCD采集设备Fig.9.(color on line)Experim ental setup:a,laser source; b,a rectangu lar op tical glass cell fixed on a rotation stage; c,beam-sp litter cube;i,beam-sp litter;e,lens;f,attenuator;g,hom e-m ade counter;h,CCD cam era.

测量开始前需要对系统进行初始位置调零,保证样品与入射光垂直,即旋转角度为0.调零后控制CCD相机采集此时的干涉条纹图如图10(a)所示,控制转动台旋转20◦,光电计数器同步计数,转动结束后显示条纹移动数为246,同时控制CCD相机采集此时的干涉条纹图如图10(b)所示.通过分析可知当光通过空比色皿,即比色皿两边均为空气时,旋转比色皿对CCD采集的干涉条纹图没有影响,条纹图始终保持不变,所以可以认为加入二次蒸馏水后旋转比色皿时干涉条纹的移动均是由比色皿内的二次蒸馏水引起,所测得的厚度分布为比色皿中水的厚度分布,即为比色皿内部厚度分布.通过计算得到的比色皿厚度分布如图10(c)所示,图标单位为µm.可以看出比色皿厚度分布基本均匀,约为1.003×104µm,同时从图10(c)也可以看出比色皿确实存在一定的厚度差.为了更清楚地展现厚度差大小,将图10(c)减去最小厚度值,得到的厚度梯度如图10(d)所示,可以看到厚度差为微米量级.进一步计算得到厚度差的峰峰值为9.92µm,均方根值为2.2µm.

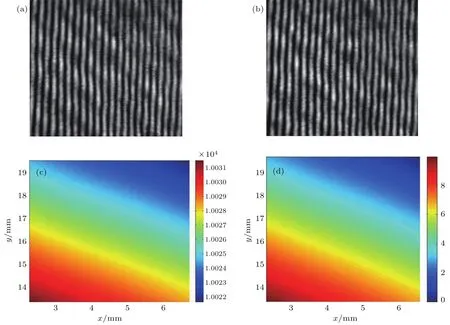
图10 (网刊彩色)待测比色皿平整度检测试验结果,比色皿在(a)初始位置和(b)旋转20◦后采集的干涉条纹图;图(c)为试验计算出的比色皿厚度分布图;图(d)为图(c)减去最小值得到的厚度梯度分布Fig.10.(color on line)The experim ental resu lts for cuvette:The interferogram w hen the sam p le at(a) the initial position and(b)rotated by 20◦;(c)the calcu lated thickness d istribu tion and(d)the calcu lated thickness diff erence distribution.

为了验证实验结果的准确性,我们将未加入二次蒸馏水时采集到的干涉条纹图与加入后采集得到的干涉条纹图之间的相位差进行了计算,根据两者之间的相位差分布可以计算得到比色皿厚度梯度分布,结果如图11所示,图11(a)为未加蒸馏水时采集到的干涉条纹图,图11(b)为加入蒸馏水后采集到的干涉条纹图,图11(c)为计算得到的比色皿厚度梯度分布,图11(d)为图11(c)与图10(d)之间的差值,其峰峰值为0.569µm,均方根值为0.131µm.这进一步表明我们所提出的方法具有超高精度和稳定性.

所提出的测量装置的测试过程耗时在10 s左右,这是受所使用的光电计数器时间分辨率限制,因此测量装置对稳定性具有较高的要求.为了测试所提出的干涉仪在实验环境下的稳定性和可重复测试能力,我们在30m in时间内连续采集干涉条纹图,采样时间间隔是5 s.通过分析前后两个时间点采集的干涉条纹图之间的条纹移动数来检验装置的稳定性.实验结果如图12所示,蓝色是一个像素点前后两个时刻条纹移动数随时间的变化情况,平均值为0.0004,均方根值为0.0023;红色是整个测试面前后两个时刻条纹移动数的均方根值随时间变化情况,平均值为0.0012,均方根值为0.0008.综上可见本测量装置具有相当高的稳定性和可重复测量能力,我们将其归功于干涉仪的共光路设计.

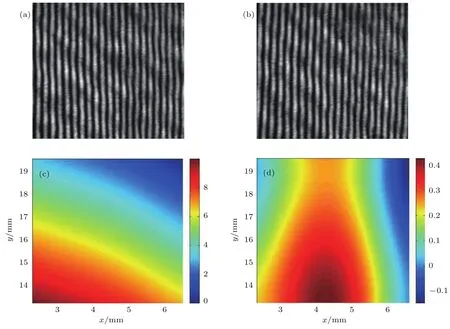
图11 (网刊彩色)待测比色皿平整度检测试验结果 (a)无待测样品和(b)待测样品在初始位置采集的干涉条纹图;(c)根据(a)和(b)计算得到的样品厚度差分布和(d)两种方法计算厚度差之差Fig.11.(color on line)The exp reim ental resu lts for cuvette:The interferogram(a)w ithout and(b)w ith sam p le at the initial position;(c)is the calcu lated thickness diff erence d istribu tion from(a)and(b);(d)is the error distribution between two ways.

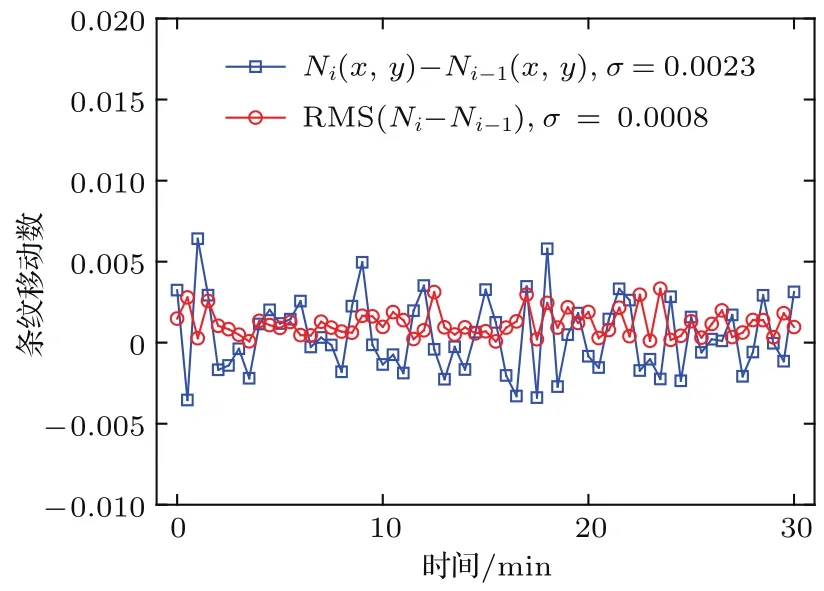
图12 (网刊彩色)装置稳定性和可重复测试能力分析,其中,蓝色曲线是单个像素点前后两个时刻条纹移动数随时间的变化情况;红色曲线是整个测试面前后两个时刻条纹移动数的均方根值随时间变化情况Fig.12.(color on line)Stability and repeatability test for the p roposed setup. Fringe shift num ber of a pixel(b lue curve)and root m ean square(RMS)of fringe shift num ber d istribu tion(red cu rve)change w ith tim e.

5 结 论

本文在实验室建立起一套基于菱形分光棱镜干涉的用于检测透明介质平整度和均匀性的干涉仪测量系统,文中给出了测量原理,通过理论分析、数值仿真和光学实验对系统进行了可行性、准确性和实用性分析,此外,还通过分析前后两个时间点采集的干涉条纹图之间的条纹移动数来检验装置的稳定性.结果表明本测量装置具有系统非接触、高精度和高稳定性等优点,且相较于现有的扫描式的测量方法而言时间成本和装置成本均大大降低,可以进一步推广到平板玻璃生产的在线检测、加工应用等领域.但待测样品大小受激光光束、旋转平台和光学系统口径大小限制不能太大,且本系统的自动化的数据处理程序以及集成化还有待进一步的研究.

参考文献

[1]Chen L F,Ren Y Q,Li J 2010 Opt.Eng.49 050503

[2]Jiang X Q,W ang K W,Gao F,M uham edsalih H 2010 Appl.Opt.49 2903

[3]W ang D D,Yang Y Y,Chen C,Zhuo Y M 2011 Appl. Opt.50 2342

[4]Chen L F,Guo X F,Hao J J 2013 Appl.Opt.52 3655

[5]Zhang T,Feng G Y,Song Z Y,Zhou S H 2014 Opt. Comm un.332 14

[6]Lan B,Feng G Y,Zhang T,Zhou SH 2017 J.M od.Opt. 64 8

[7]W ang Y,Q iu L R,Yang JM,ZhaoW Q 2013Optik 124 2825

[8]BaiH Y,Shan M G,Zhong Z,Guo L L,Zhang Y B 2015 Opt.Lasers Eng.75 1

[9]Bai Y,Zhao W J,Ren D M,Qu Y C,Liu C,Yuan J H, Q ian L M,Chen Z L 2012 Acta Phys.Sin.61 094218 (in Chinese)[白岩,赵卫疆,任德明,曲彦臣,刘闯,袁晋鹤,钱黎明,陈振雷2012物理学报61 094218]

[10]Du J,Zhao W J,Qu Y C,Chen Z L,Geng L J 2013 Acta Phys.Sin.62 184206(in Chinese)[杜军,赵卫疆,曲彦臣,陈振雷,耿利杰2013物理学报62 184206]

[11]W ang Y,Qiu L R,Song Y X,Zhao W Q 2012 M eas. Sci.Techno l.23 055204

[12]Takeda M,Ina H,Kobayashi S 1982 J.Opt.Soc.Am. 72 156

[13]Du Y Z,Feng G Y,Li H R,Vargas J,Zhou S H 2012 Opt.Express 20 16471

[14]Lan B,Feng G Y,Dong Z L,Zhang T,Zhou S H 2016 Optik 127 5961

[15]Ferrari J A,Frins E M 2007 Opt.Comm un.279 235

PACS:95.75.Kk,43.60.T j,95.75.M n,78.20.CiDOI:10.7498/aps.66.069501

A sing le-elem ent in terferom eter for m easu ring parallelism and un iform ity of transparent p late∗

Lan Bin1)Feng Guo-Ying1)†Zhang Tao1)Liang Jing-Chuan1)Zhou Shou-Huan1)2)

1)(Institute of Laser and M icro/Nano Engineering,College of Electronics and Inform ation Engineering,Sichuan University,

Chengdu 610064,China)
2)(North China Research Institu te of E lectro-optics,Beijing 100015,China)
(Received 10 Novem ber 2016;revised m anuscrip t received 29 Novem ber 2016)

The transparent p lates(such as organic glass,p lastic p late)are w idely used in the construction industry,high-tech products and scientific research app lications,and its parallelism and uniform ity measurement in themanu facture and quality control becom em ore and m ore inevitable.Interferom eter is a label-free,high-p recision,and high-effi cient device that can be used in m any fields.According to a single-elem ent interferom eter,we demonstrate a m easurem ent for the parallelism and uniform ity of transparent medium.Beam-sp litter cube is a key com ponent.Half of p lane wave laser source passes through them easured m edium and the rem aining half directly passes through the air,then these two halves w ith diff erent optical pathsmeet in the beam-sp litter cube.The parallelism or uniform ity is determ ined by calcu lating interference fringe shift number during rotating them easured sam p le.The coherent beam is divided into two parts by a beam-sp litter,one passes through the lens and then arrives at a photoelectric counter,and the other arrives at the observation p lane of the charge-coup led device.The photoelectric counter is used to count the integer part of fringe shift number during rotating the sam p le;and the decim al part can be detected by calculating the phase diff erence of the two interferogram s captured before and after rotation.The m easurem ent princip le of the p roposed device is analyzed in detail,and the numerical simulations of the fringe shift number and the gray level changing w ith the sam p le rotation angle,the thickness and the refractive index of the sam p le are carried out.The simulation resu lts show that the bigger the rotation angle,thickness and refractive index of the sam p le,the greater the fringe shift number w illbe.Therefore,the measurement accuracy can be im p roved by increasing the rotation angle and the thickness of the sam p le.In addition,we also simu late them easurem ent processes of two kinds of sam p les,which are unparallel and inhom ogeneous transparent p lates.The simulation resu lts p rove the feasibility and high accuracy of the proposed method.Finally,the optical experiment is conducted to demonstrate the practicability of the present device.The parallelism of a cuvette used for m ore than one year,is tested by our device.The resu lts show that the diff erence in thickness between the cuvettes is on a m icron scale,the peak-valley(PV)value is 9.92µm,and the root mean square(RMS)value is 2.2µm.And the diff erence between the contrast test resu lts and the results from the proposed m ethod is very sm all,the PV value is 0.569µm,and the RMS value is 0.131µm.The stability and repeatability of the proposed setup are tested in the experimental condition.Themean value and standard deviation of the fringe shift number during 30 m in are 0.0012 and 0.0008,respectively.These results further testify the high accuracy and stability of our m ethod.In conclusion,the perform ance of our m easurem ent m ethod is dem onstrated w ith num erical simulation and optical experim ent.

interferometry,phasemeasurement,image processing,refractive index

10.7498/aps.66.069501

∗国家自然科学基金(批准号:11574221)资助的课题.

†通信作者.E-m ail:guoing_feng@scu.edu.cn

*Pro ject supported by the National Natural Science Foundation of China(G rant No.11574221).

†Corresponding author.E-m ail:guoing_feng@scu.edu.cn