人类心室组织中波斑图引起的后除极化研究∗
王小艳 汪芃 唐国宁
(广西师范大学物理科学与技术学院,桂林 541004)
(2016年10月10日收到;2016年11月27日收到修改稿)
人类心室组织中波斑图引起的后除极化研究∗
王小艳 汪芃 唐国宁†
(广西师范大学物理科学与技术学院,桂林 541004)
(2016年10月10日收到;2016年11月27日收到修改稿)
突然的心脏死亡常常由心脏的心律失常引起,而心律失常常与后除极化有关.本文采用人类心脏模型研究了二维心肌组织中存在螺旋波或其他波斑图下后除极化的发生,通过改变L型钙电导和快钾电导让螺旋波演化,观察后除极化在空间的分布.研究发现:在单细胞和一维情况下不出现后除极化时,螺旋波可导致相II型和相III型早期后除极化、延迟后除极化、增强的自动性,以及延时激发和延时增强自动性的出现;还观察到螺旋波导致膜电位在动作电位I期出现弱振荡;后除极化一般出现在螺旋波波核区域,它是由螺旋波的相奇异点引起.后除极化也可以分布在更大的范围,当参数选取适当时,出现早期后除极化、延迟后除极化、增强自动性的空间点在空间呈螺旋线分布,展示记忆效应.通过观察各种离子电流变化发现:当激发细胞的钠电流很小时可诱发L型钙电流、钠钙交换电流的增大和慢钾电流、快钾电流的减少,导致各种后除极化的产生,因此增大钠电流可有效抑制后除极化的发生.
螺旋波,后除极化,增强自动性,Ten Tusscher-Noble-Noble-Panfi lov模型
1 引 言
实验结果表明[1],在可激发介质中普遍存在的螺旋波主要以再入波的形式在心脏中传播,由于它以高于心脏自然起搏频率重复通过心脏组织,因此人们广泛认为大多数危险的心律失常是由再入波引起的[2],螺旋波破碎将导致心室纤维性颤动[3].然而,由于心脏组织结构和心肌细胞的膜电流十分复杂,使得要掌握再入波引起的心动过速机制十分困难.目前人们对心脏中螺旋波动力学的研究已经取得许多研究成果[4−9],已经发现[2,5]心脏中的螺旋波有多种破碎机制,如动作电位恢复曲线的斜率大于1、动作电位持续时间的双稳定性和迟滞现象、2:1阻滞的形成、波头的多普勒运动、双相动作电位恢复曲线、异常的传导速度都可以导致螺旋波破碎.由于这些螺旋波破碎机制是采用动物心脏模型获得的,在一般的反应扩散系统中,上述螺旋波破碎机制只有少部分会出现,这说明只有采用心脏模型才能有效掌握心动过速产生的机制.过去的十多年来,人们已经提出了多个人类心脏模型[9−13],人类心脏模型与动物心脏模型有很大差别[14],采用人类心脏模型研究心脏中的螺旋波动力学和破碎机制,对掌握心室纤维性颤动产生机制和抗心律失常药物的设计具有重要意义.
在心脏中存在一种特殊的心律失常,它与心肌细胞后除极化(包括增强自动性)有关.本文将后除极化分为早期、延迟后除极化和增强自动性,早期后除极化(EAD)是在动作电位的复极化阶段膜电位出现反常振荡现象,EAD又可以分成相II和相III型EAD,因为它们分别在动作电位处于II期和III期阶段时细胞出现去极化,它们通常在具有先天或后天长QT综合症和心衰病人中被观察到[15],此外药物[16]、氧化应激[17]、纤维化[18]都可以使心脏出现EAD.延迟后除极化(DAD)是在动作电位完全复极化后膜电位出现的反常振荡现象,而增强自动性(EA)是在动作电位复极化后膜电位自发出现除极化现象[19].许多实验[20,21]和计算机模拟[15,22]在细胞水平上研究了EAD产生的离子机制.研究发现:在单细胞出现后除极化的情况下,螺旋波态下也可以出现EAD[22].从细胞层次上看,通常增加内向或减少外向电流、肌质网中的钙过载都可以导致EAD[15],出现DAD的主要原因是自发的脂质网钙释放激活钙敏感内向电流(例如钠钙交换电流)而导致后除极化[23].然而到目前为止,在二维介质和整个心脏中EAD,DAD和EA是如何出现的仍不清楚,特别是在螺旋波态下这些现象如何出现缺乏研究.对这些问题的研究有助于人们了解EAD,DAD和EA在组织层次上产生的机制,并提出有效方法控制EAD,DAD和EA的产生,防止心律失常和心颤的发生.
本文采用Ten Tusscher等[10]提出的人类心脏模型研究心室组织中的螺旋波动力学.通过改变L型钙电导和快钾电导观察后除极化的发生,我们发现:在单细胞和一维情况下,系统不会出现后除极化,但是相同参数下,如果二维系统存在螺旋波或其他波斑图,则在系统中可观察到各种后除极化现象,除观察到相II和相III型EAD,DAD和EA外,我们还观察到在动作电位I期膜电位出现弱振荡现象,以及EAD,DAD和EA大范围出现等现象.这些研究结果为了解EAD,DAD和EA产生机制提供了有用信息.
2 数学模型
我们使用的数学模型是Ten Tusscher等[10]在2004年提出的人类心脏模型,文献上一般称为Ten Tusscher-Noble-Noble-Panfi lov(TNNP)人类心脏模型,该模型使用的实验数据涉及主要的离子电流,因此可以用来研究人类心脏再入性心动过速,该模型动力学方程如下[10]:
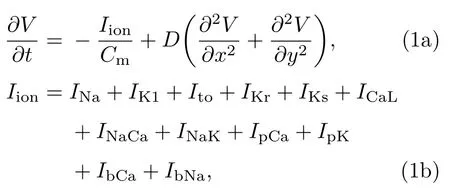
式中V是膜电位(单位是mV);t是时间(单位是ms);Cm=1.0µF/cm2是细胞单位面积的电容; D=0.00154 cm2/m s是扩散系数;Iion是细胞膜的总离子电流,其中,INaCa为Na+/Ca2+交换电流, INaK为Na+/K+泵电流;含角标Na,K,CaL,p和b符号分别代表钠电流、钾电流、L型钙电流、泵电流和背景电流.
考虑到细胞老化和心衰可导致钾电流减少和L型钙电流增加,也观察到导致钾电流增加和L型钙电流减少的现象.为了研究不同参数下后除极化在空间的分布,我们将L型钙电流和快速延迟整流钾电流的最大电导率分别增大χCal和χKr倍,即将原模型中L型钙电流的最大电导率由GCal=0.175 cm3/(µF·ms)改为χCalGCal,将快钾电流的最大电导率由GKr=0.096 nS/pF改为χKrGKr,如无特别说明,其他参数与原始模型一致,在此情况下研究在不同参数(χCal,χKr)下螺旋波的动力学行为.
利用数值方法求解方程(1)时,放大倍数χCal在[0,2]范围内取值,χKr在[0,9.5]范围内取值.取细胞外钠、钙、钾离子和肌质网中自由钙离子浓度分别为Nai=11.6 mM,Cai=0.00002 mM, Ki=138.3 mM和Casr=0.2 mM,取钙泵电流的最大电导率为GpCa=0.825 nS/pF,其他参数选择文献[10]给出的心外膜细胞参数.空间步长和时间步长分别取Δx=Δy=Δ=0.02 cm和Δt=0.02m s,本文取大小为30 cm×30 cm二维介质,被离散成1500×1500个格点,格点坐标用(i,j)标记,其中i,j取整数.使用无流边界条件,时间求导使用一阶欧拉向前差分法,空间二阶导数采用中心差分方法,模拟时间长度为8 s.
3 数值模拟结果
首先选取5组参数(χCal,χKr)=(0.0,0.0), (2.0,0.0),(0.0,9.5),(1.0,1.0),(2.0,9.5),观察在单细胞下(D=0),细胞动作电位是否出现后除极化现象,所得结果如图1所示.从图1可以看出,这5组参数都没有出现EAD和DAD,因此我们认为在χCal和χKr的取值范围内也不会出现后除极化现象.由于不同参数下的静息膜电位在(−86.0,−86.6)mV范围内变化,因此本文把细胞从静息态(V≈−86 mV)被激发后回到静息态(本文取V=−85 mV)所经历的时间称为动作电位持续时间,记为Tapd.从图1还可以看出,增大χCal将导致Tapd的增加,增大χKr则使Tapd减少.在一维情况下,我们也得到与图1类似的结果.
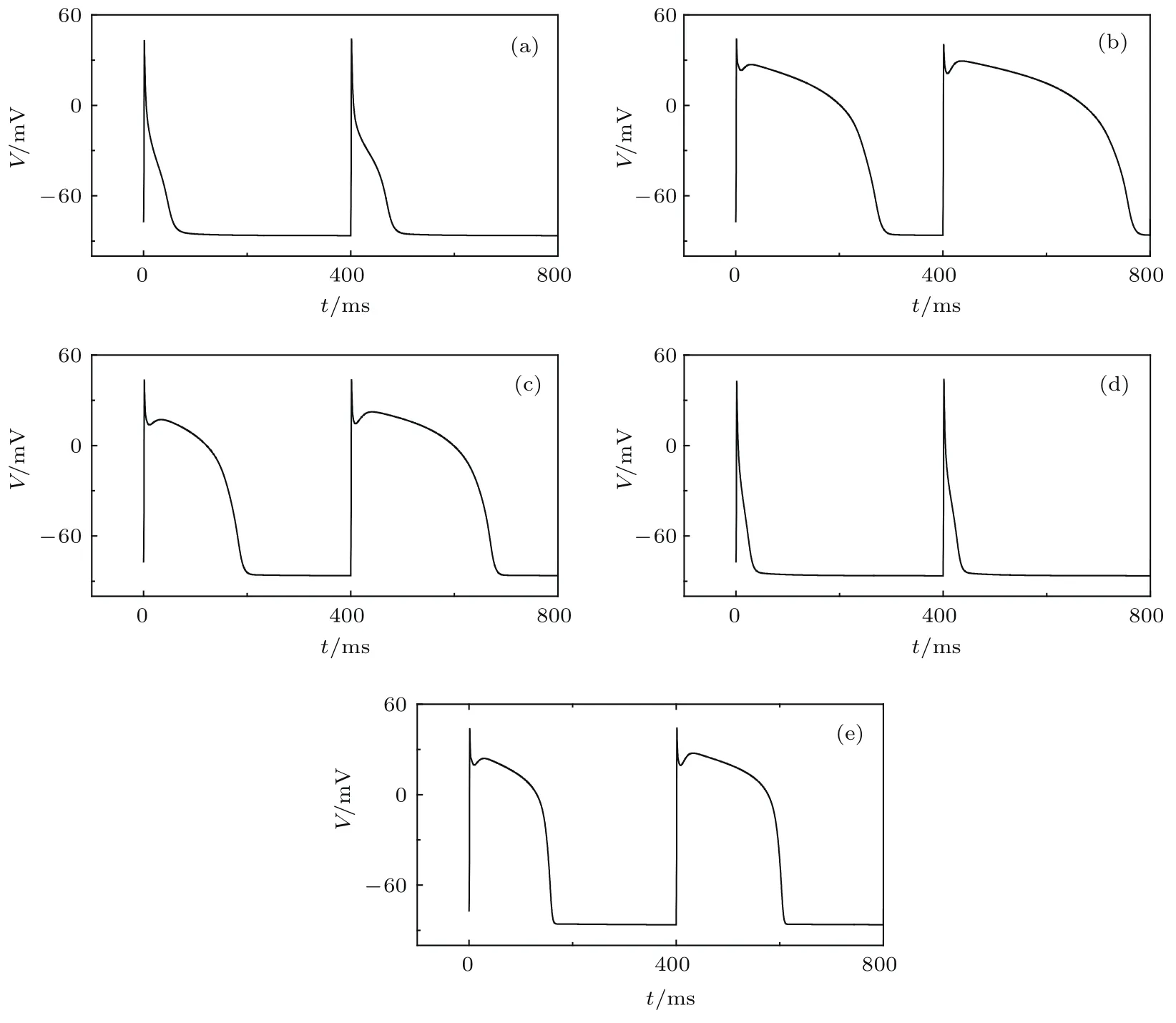
图1 不同参数下单细胞膜电位随时间的变化 (a)χCal=0.0,χKr=0.0;(b)χCal=2.0,χKr=0.0; (c)χCal=1.0,χKr=1.0;(d)χCal=0.0,χKr=9.5;(e)χCal=2.0,χKr=9.5Fig.1.Evolution ofm embrane potential for diff erent param eters:(a)χCal=0.0,χKr=0.0;(b)χCal=2.0, χKr=0.0;(c)χCal=1.0,χKr=1.0;(d)χCal=0.0,χKr=9.5;(e)χCal=2.0,χKr=9.5.
下面我们在二维情况下研究在螺旋波和其他波斑图下后除极化的空间分布. 首先在χCal= χKr=1.0的情况下产生螺旋波作为初态,然后改变参数χCal和χKr观察螺旋波的演化,并记录空间各点是否出现后除极化现象.为了简单起见,我们这样分类后除极化:如果某个心肌细胞在II和III期复极化过程中,在细胞膜电位大于等于−85 mV情况下出现后除极化现象,我们就认为这种后除极化就是EAD;相反,如果后除极化发生在膜电位小于−85 mV,我们把这种后除极化称为DAD;如果后除极化后,膜电位的上升幅度超过70mV,则我们称这种后除极称为EA.
为了直观地反映后除极化在时空上的分布,我们将后除极化标记在斑图中.标记方法如下:为了解t时刻后除极化的空间分布,则选t时刻膜电位斑图(灰度图)作为标记斑图,假设空间r点最近一次激发发生在t−t0时刻,下一次激发发生在t+t1时刻,如果在[t−t0,t]期间出现EAD,DAD和EA,则在斑图中分别用蓝色点、红色点和绿色点标记.由于在模拟中发现可能[t−t0,t]期间同时出现EAD和EA情况,对于这种情况我们也标记为蓝色点.这种标记方法可能会出现这样的情况:如果标记有后除极化的空间点在t时刻之前已经回到静息态,这时标记点出现在膜电位斑图的暗区域.
在数值中我们观察到,在改变参数后系统仍维持螺旋波状态,或者螺旋波破碎后形成规则斑图(包括多螺旋波)或时空混沌.在系统仍维持螺旋波状态的情况下观察到:螺旋波可以导致EAD, DAD,EA以及延迟激发现象,EAD,EA,DAD一般在螺旋波的波核区域出现,但是在这个区域DAD出现的概率比较小,在少数参数下,EAD, EA,DAD可出现在其他区域,而且出现EAD,EA, DAD的空间点可形成螺旋线,这种大范围出现EAD,EA,DAD却不会导致螺旋波的破碎令人意外.在螺旋波出现破碎情况下观察到:EAD,DAD, EA还出现在波核之外区域,这时EAD,EA,DAD既可呈零散分布,也可在螺旋波破碎过程中大范围出现,且出现EAD,EA,DAD的空间点呈螺旋线分布,依赖参数选取.下面我们给出某些参数下EAD,EA,DAD的空间分布.
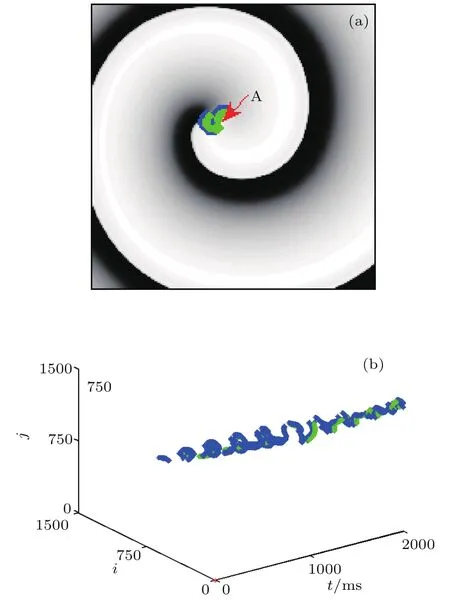
图2 在χCal=1.0和χKr=1.0时,(a)t=1000 m s时刻的膜电位斑图和(b)后除极空间分布随时间变化,蓝色点和绿色点分别代表EAD和EAFig.2.(a)Pattern of m em brane potential at t= 1000 m s and(b)evolution of spatial distribu tion of afterdepolarization forχCal=1.0 andχKr=1.0.The b lue points and green points rep resent the EAD and EA,respectively.
图2给出了在χCal=1.0和χKr=1.0情况下在t=1000 ms时刻的膜电位斑图和后除极化空间分布随时间变化,在此参数下系统为螺旋波态.从图2可以看出,螺旋波导致了EAD和EA的出现,而且都分布在靠近波头的波后处(即波核区).图3给出了图2(a)箭头所指的空间点(666, 885)的膜电位和钠电流随时间的变化.从图3可以看出,当激发细胞的钠电流比较小时,通常出现EAD、EA、延迟激发和延时EA,相II型和相III型EAD分别如图3(a)中B和D点所示,延时EA和EA分别形成了如图3(a)中A和E峰,延时激发如图3(a)的C和F点,对比图3(b)可以看出后除极化和延时激发不是钠电流导致的.为了了解产生EAD和EA的机制,图4给出了与图3对应空间点的L型钙电流、慢钾电流、钠钙交换电流和快钾电流随时间的变化曲线.从图4可以看出,产生EAD的原因是增加了内向电流(例如ICal和INaCa)同时减少外向电流(例如IKs和IKr),EA产生的机制是 IKs和IKr几乎减少到0,同时ICal大幅度增加.图2和图3的结果表明:EAD和EA这种振荡是无规的,且分布在特定区域,无EAD时膜电位振荡是规则的,因此图2所示的螺旋波就是通常所说的螺旋波混杂态,这种状态最早在振荡介质中被发现[24],现在心脏组织中也被观察到,表明EAD和EA的出现不是偶然的,它是螺旋波相奇异点导致的.
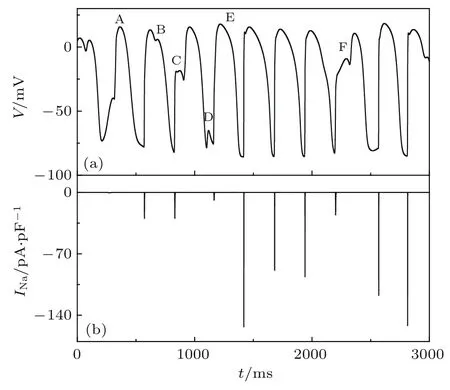
图3 在χCal=1.0和χKr=1.0时,图2(a)箭头所指空间点的(a)膜电位和(b)钠电流随时间的变化Fig.3.Evolu tion of(a)m em b rane potential and(b) sodium current at the grid point indicated by arrow show n in Fig.2(a)forχCal=1.0 andχKr=1.0.
当螺旋波漫游或破碎成规则斑图或时空混沌态时,EAD,DAD和EA通常零散出现,图5给出了在χCal=0.5和χKr=5.0情况下螺旋波漫游出系统的过程,图6给出了χCal=1.0和χKr=8.5情况下螺旋波破碎过程,最后形成多螺旋波.从图5和图6可以看出,螺旋波导致EAD,DAD和EA不时出现,且分布比较零散,且主要的后除极化是EAD.
当参数选取适当时,在螺旋波破碎过程中后除极化分布呈现十分有规律的大范围连续分布.图7给出了在χCal=1.5和χKr=0时螺旋波的破碎成规则斑图的过程,其中图7(e)和图7(f)斑图在后续演化中会交替出现.从图7可以看出,在该参数下,螺旋波导致大范围后除极化,EAD,DAD和EA空间点呈螺旋线状分布,最后螺旋波演化成规则斑图.
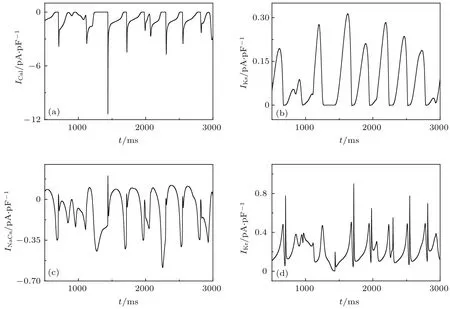
图4 在图3的参数和相同空间点下(a)L型钙电流ICal、(b)慢钾电流IKs、(c)钠钙交换电流INaCa、(d)快钾电流IKr随时间的变化Fig.4.Evolution of(a)L-type calcium cu rrent ICal,(b)slow potassium current IKs,(c)sod ium calcium exchange current INaCa,and(d)quick potassium current IKr.The param eters and grid points are the sam e as the Fig.3.

图5 在χCal=0.5和χKr=5.0时不同时刻的膜电位斑图 (a)t=200 m s;(b)t=320 m s;(c)t=1200 m s; (d)t=5000 m sFig.5. Patterns of m em b rane potential at diff erent tim e m om ents forχCal=0.5 andχKr=5.0: (a)t=200 m s;(b)t=320 m s;(c)t=1200 m s; (d)t=5000 m s.

图6 在χCal=1.0和χKr=8.5时不同时刻的膜电位斑图 (a)t=500 m s;(b)t=3500 m s;(c)t=3960 m s; (d)t=7200 m sFig.6. Patterns of m em b rane potential at diff erent tim e m om ents forχCal=1.0 andχKr=8.5: (a)t=500 m s;(b)t=3500 m s;(c)t=3960 m s; (d)t=7200 m s.
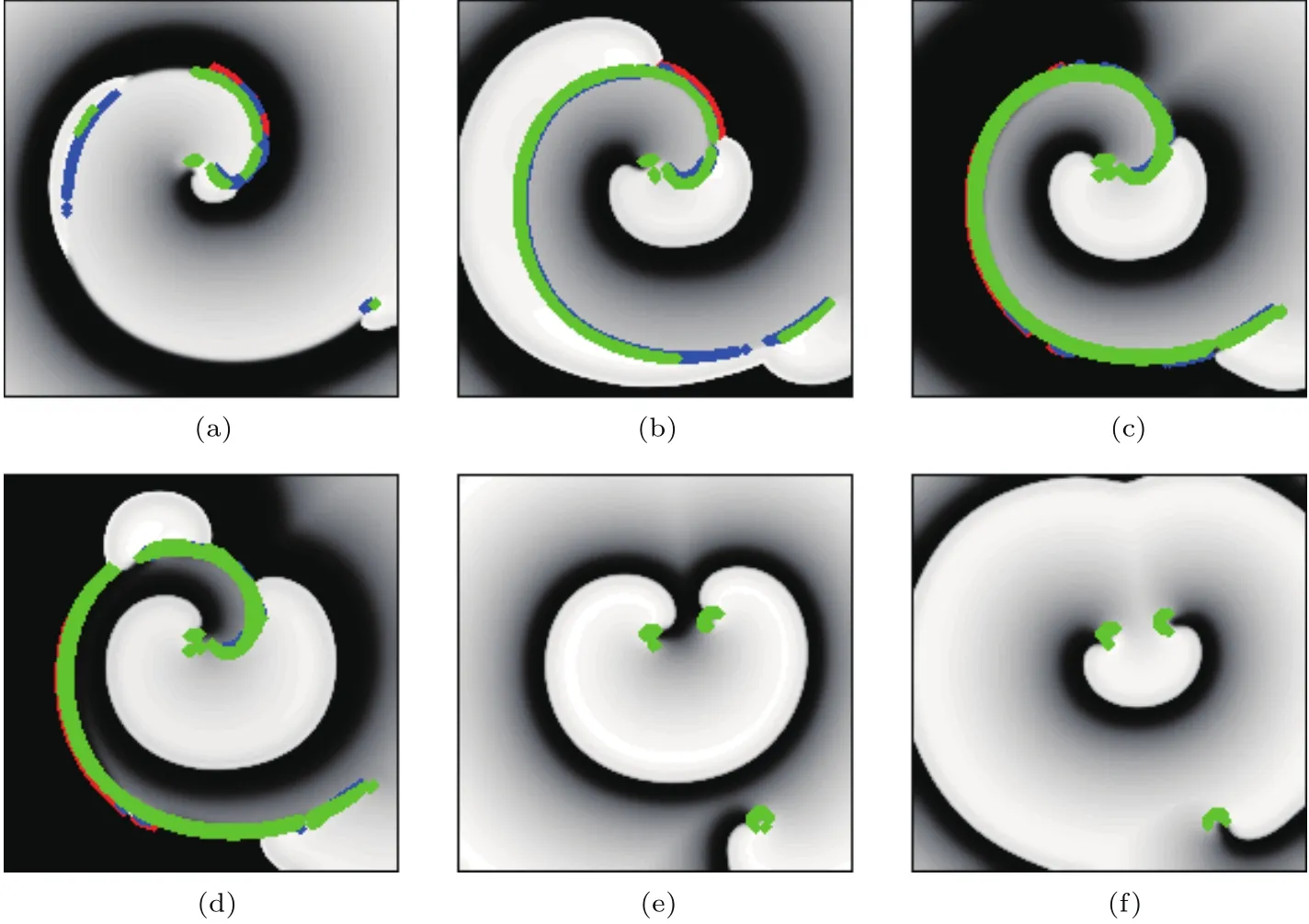
图7 在χCal=1.5和χKr=0.0时不同时刻的膜电位斑图 (a)t=540 m s;(b)t=620 m s;(c)t=980 m s; (d)t=1040 m s;(e)t=1420 m s;(f)t=1520 m sFig.7.Patterns of m em b rane potential at d iff erent tim e m om ents forχCal=1.5 andχKr=0.0:(a)t= 540 m s;(b)t=620 m s;(c)t=980 m s;(d)t=1040 m s;(e)t=1420 m s;(f)t=1520 m s.
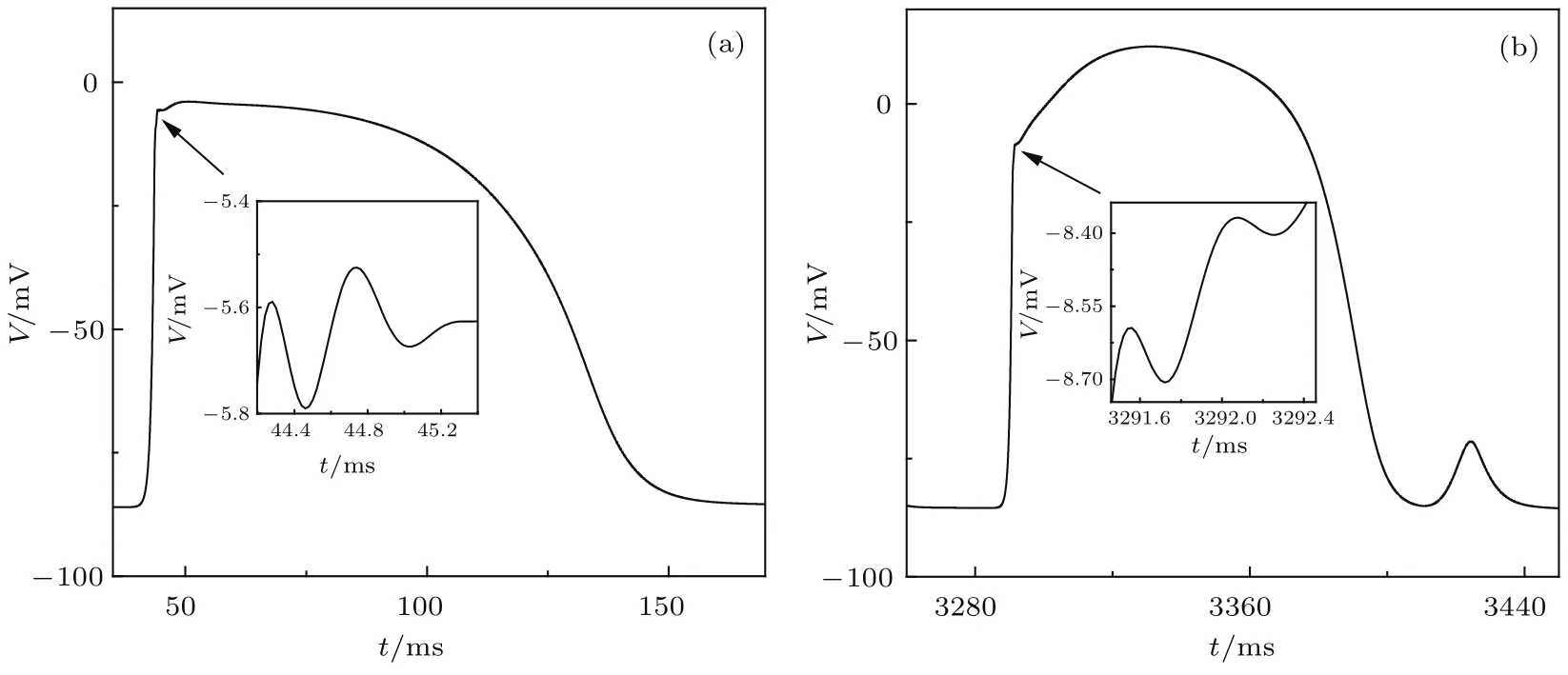
图8 不同参数下空间某一点膜电位随时间的变化,图中插图为箭头所指局部曲线的放大 (a)χCal=1.5, χKr=0.0;(b)χCal=1.0,χKr=9.5Fig.8.Evolu tion ofm em brane potential at a grid point for diff erent param eters(the inset is the b lowup of the local curve indicated by arrow):(a)χCal=1.5,χKr=0.0;(b)χCal=1.0,χKr=9.5.
在数值模拟中,除发现螺旋波导致EAD,DAD和EA外,我们还观察到在动作电位I期出现膜电位弱振荡现象,如图8所示,我们把这种膜电位振荡称为相I型振荡.图8还显示出现了DAD,表明相I型后振荡可以与后除极化在同一个动作电位出现.图8是随意选取的两组参数,选其他参数也可以观察到相I型振荡现象.
为了了解不同参数下螺旋波的动力学行为和后除极化分布情况,图9给出了在χCal-χKr平面上的相图.从图9可以看出,在所有参数下螺旋波都可以导致EAD出现,有些参数下还可以导致DAD和EA出现,特别是在L型钙电导较大时导致出现大范围后除极化连续分布.如果这时快钾电导接近0,则这种大范围后除极化导致螺旋波破碎(参见图7);如果这时快钾电导很大,这种大范围后除极化则不会导致螺旋波破碎,说明后除极化不一定导致螺旋波破碎.从图9还可以看出增大快钾电导不能有效消除后除极化,但是抑制快钾电流容易导致EA出现,抑制L型钙电流可以抑制EA出现.

图9 在χCal-χKr平面上的相图,其中,空心符号为单个螺旋波,实心符号为螺旋波破碎成多螺旋波、规则斑图或时空混沌斑图;○表示螺旋波导致EAD,DAD,EA出现;□表示螺旋波只导致EA和EAD出现;△表示螺旋波只导致EAD和DAD出现;▽表示螺旋波只导致EAD出现;♢表示螺旋波消失,后除极化主要为EAD;表示螺旋波导致大范围出现EAD以及EA或DAD,后除极化空间点可呈螺旋线状分布;⋆代表在螺旋波破碎成规则斑图过程中出现大范围的后除极化;表示在螺旋波转变为混沌态过程中出现EAD,DAD,EAFig.9.Phase d iagram in theχCal-χKrparam eter p lane.The hollow sym bols rep resent the states of a single sp iral wave.The solid sym bols rep resent that spiral wave b reaks up into m u ltip le spiral waves,regu lar pattern or spatiotem poral chaos.Circle,sp iral wave resu lts in the occurrence of EAD,DAD and EA;square,sp iral wave only resu lts in the occurrence of EAD and EA;up-triangle,spiralwave on ly results in the occurrence of EAD and DAD;down-triangle,spiralwave on ly resu lts in the occu rrence of EAD;rhom bus,sp iralwave disappears,and afterdepolarization m ain ly is EAD;pentagon,spiral wave resu lts in the occu rrence of EAD as well as EA or DAD in a w ide range of space,and afterdepolarization can exhibit sp iral distribu tion;solid pentagon,afterdepolarization occurs in a w ide range of space in the p rocess that spiral wave breaks up into regular pattern;solid circle,the phenom ena of EAD,DAD and EA occu r in the p rocess that sp iral wave breaks up into spatiotem poral chaos.
为了更直观地了解后除极化空间分布,图10给出了不同参数下后除极化的空间分布随时间的变化,它除了反映图5和图7参数下后除极化的空间分布,还给出了其他有特色的后除极化空间分布.从图10可以看出,在发生后除极化的空间点中,一般出现EAD的空间点比出现DAD和EA的空间点多很多,少数情况只出现EAD,如图10(c)所示.少数情况是出现EA或DAD的空间点比出现EAD的空间点多许多,分别如图10(b)和图10(e)所示.图10(b)显示在螺旋波态下系统周期性出现EA,有些格点可以连续出现EA,有些格点只连续出现2次EA,分别展示出长期记忆和短期记忆效应.显然EA空间点比出现EAD的空间点多,DAD没有出现.图10(e)显示在螺旋波态下系统在某些时刻出现DAD的空间点呈螺旋线状分布和片状分布,比出现EAD和EA的空间点多许多,也展示记忆效应.图10(f)显示在螺旋波破碎成时空混沌过程中EA和DAD零散出现,主要是出现EAD.
上述模拟结果表明:只有少数参数下系统可在大范围内出现后除极化,而且只在螺旋波态和螺旋波破碎过程中出现如图10所示的大范围后除极化,这表明系统存在两种状态,一种是后除极化少发状态,另一种是后除极化多发状态,一旦系统处于后一种状态,就会导致心衰或心脏死亡.我们发现增加钠电流可以有效抑制大范围出现后除极化,例如当细胞被激发时,只要钠电流小于−10 pA/pF,就人为将钠电流增大到−140 pA/pF,直到膜电位增加到0 mV才让钠电流按正常规律变化,这样就可以消除大范围出现后除极化,但是在局部仍会出现后除极化,而且这些都是激发细胞的钠电流不足引起的,这表明后除极化不仅与激发细胞的钠电流不足有关,还与波斑图动力学有关.
4 结 论
本文采用人类心室细胞动力学模型研究在系统存在螺旋波和其他波斑图的情况下后除极化的产生,在单细胞和一维情况下外部刺激不导致后除极化时,我们发现:1)螺旋波态和其他波斑图可以导致EAD、DAD、EA、延时激发、延时EA和在动作电位I期膜电位出现弱振荡现象,EAD,DAD,EA这些后除极化一般出现在螺旋波的波核处,由螺旋波相奇异点引起,因此我们首次在心脏组织中观察到螺旋波混杂态;2)当参数选取适当时,EAD, DAD,EA后除极化也可以出现在其他区域,既可以零散出现,也可以大范围出现,这时心脏系统进入大范围出现后除极化的状态,出现后除极化的空间点可呈螺旋线状分布,展示记忆效应,也可以呈片状分布;3)后除极化诱因为激发细胞的钠电流不足,增大钠电流可以有效抑制后除极化的发生,出现EAD的原因是增加了内向电流的同时减少了外向电流,EA产生的机制是 IKs和IKr几乎为0,同时ICal大幅度增加;4)大范围出现EAD和EA并不一定导致螺旋波破碎,但是螺旋波破碎总是伴随EAD,DAD和EA的出现.由于后除极化可引发向后传播的电波[22],本文研究结果可以解释如下实验观察:体外电击除颤方法并不是百分之百有效,需要多次电击或者提高电击能量才能达到除颤目的[25],这可能是在控制螺旋波的过程中引起的后除极化导致了除颤失败,因此心脏中螺旋波和时空混沌控制需要考虑后除极化的影响.心脏组织在适当的条件下会进入后除极化多发状态,如何防止这种现象的发生,本文的研究结果也为医学工作者指明了方向.
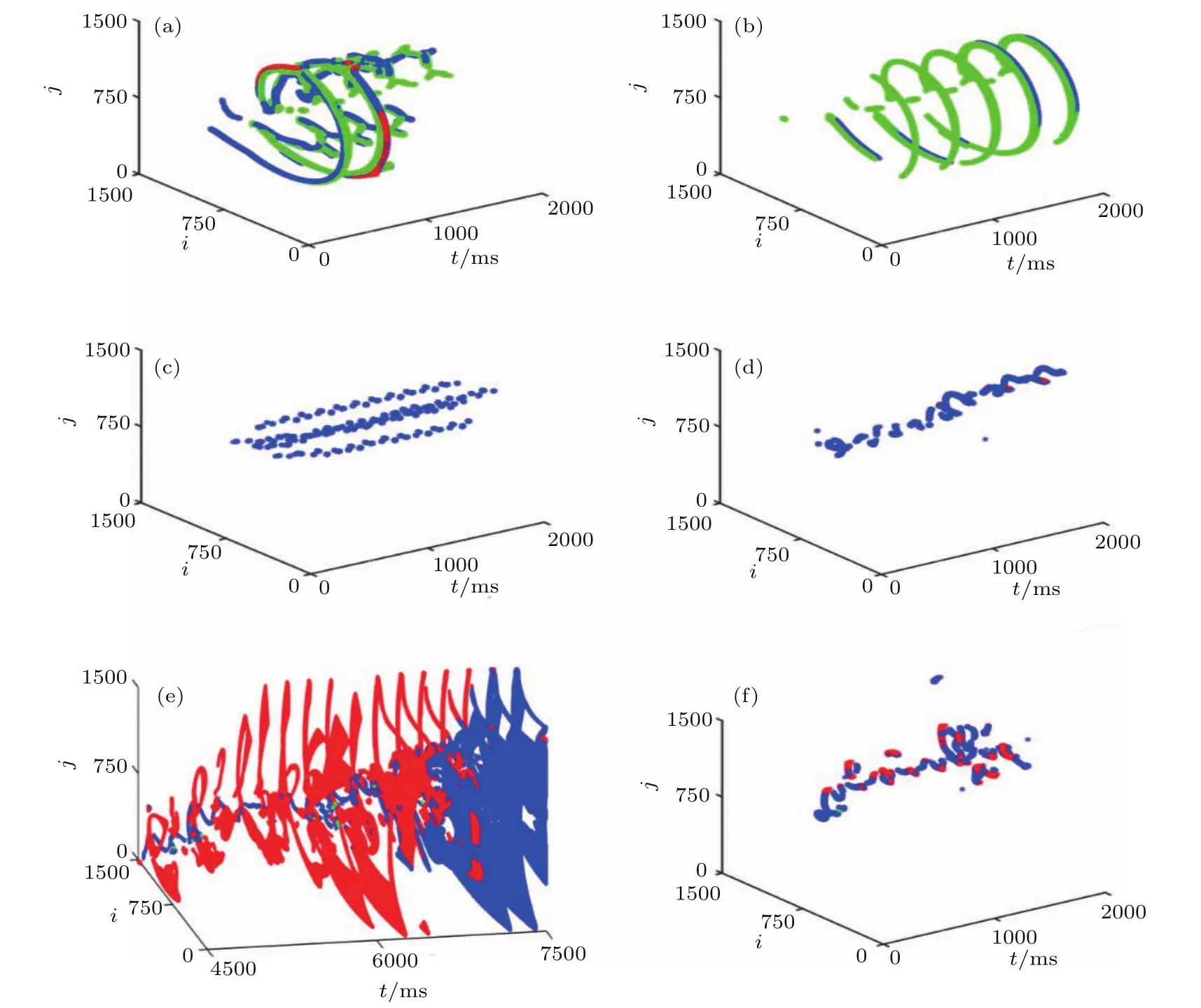
图10 不同参数下后除极化空间分布随时间变化(图中蓝色点代表EAD,红色点代表DAD,绿色点代表EA)(a)χCal= 1.5,χKr=0.0;(b)χCal=2.0,χKr=0.0;(c)χCal=0.0,χKr=9.5;(d)χCal=0.5,χKr=5.0;(e)χCal=2.0, χKr=9.5;(f)χCal=1.0,χKr=9.5Fig.10.The evolution of spatial distribution of afterdepolarization for diff erent param eters:(a)χCal=1.5, χKr=0.0;(b)χCal=2.0,χKr=0.0;(c)χCal=0.0,χKr=9.5;(d)χCal=0.5,χKr=5.0;(e)χCal=2.0, χKr=9.5;(f)χCal=1.0,χKr=9.5.The b lue,red and green points rep resent the EAD,DAD,and EA in the d iagram s,respectively.
[1]G ray R A,Jalife J,Pan fi lov A,Baxter W T,Cabo C, Davidenko J M,Pertsov A M 1995 Circu lation 91 2454
[2]Fenton F H,Cherry E M,Hastings H M,Evans S J 2002 Chaos 12 852
[3]Ouyan Q 2001 Physics 30 30(in Chinese)[欧阳颀2001物理30 30]
[4]K elderm ann R H,Ten Tusscher K H W J,Nash M P, Brad ley C P,H ren R,Taggart P,Pan fi lov A V 2009 Am. J.Physiol.Heart Circ.Physiol.296 H 370
[5]Qu Z,X ie F,Garfinkel A,W eiss J N 2000 Ann.Biom ed. Eng.28 755
[6]Cou rtem anche M 1996 Chaos 6 579
[7]Sha jahan T K,Nayak A R,Pand it R 2009 PLoS One 4 e4738
[8]K azbanov I V,C lay ton R H,Nash M P,B rad ley C P, Paterson D J,Hayward M P,Taggart P,Pan fi lov A V 2014 PLoS Com put.Biol.10 e1003891
[9]Priebe L,Beuckelm ann D J 1998 Circ.Res.82 1206
[10]Ten Tusscher K H W J,Nob le D,Nob le P J,Pan fi lov A V 2004 Am.J.Physiol.Heart Circ.Physiol.286 H 1573
[11]Iyer V,M azhari R,W inslow R L 2004 Biophys.J.87 1507
[12]G rand i E,Pasqualini F S,Bers D M 2010 J.M ol.Cell Cardio l.48 112
[13]O’Hara T,V irág L,VarróA,Rudy Y 2011 PLoS Compu t.Biol.7 e1002061
[14]Ten Tusscher K HW J,H ren R,Pan fi lov A V 2007 Circ. Res.100 e87
[15]Zim ik S,Vandersickel N,Nayak A R,Pan fi lov A V,Pand it R 2015 PLoS One 10 e0130632
[16]de FerrariG M,V iola M,D’Am ato E,Antolini R,Forti S 1995 Circulation 91 2510
[17]X ie L H,Chen F,Karagueuzian H S,Weiss J N 2009 Circ.Res.104 79
[18]K aragueuzian H S,Nguyen T P,Qu Z,W eiss J N 2013 Fron t.Physiol.4 1
[19]Schillinger K J,Patel V V 2012 J.Geriatr.Cardiol.9 379
[20]Zhao Z,W en H,Fefelova N,A llen C,Baba A,M atsuda T,Xie L H 2012 Am.J.Physiol.Heart Circ.Physiol. 302 H 1636
[21]Sato D,X ie L H,Nguyen T P,W eiss J N,Qu Z 2010 Biophys.J.99 765
[22]Vandersickel N,K azbanov IV,Nuiterm ans A,W eise L D,Pand it R,Pan fi lov A V 2014 PLoS One 9 e84595
[23]Liu M B,de Lange E,Garfinkel A,W eiss JN,Qu Z 2015 Heart Rhythm 12 2115
[24]M artens E A,Laing C R,Strogatz SH 2010 Phys.Rev. Lett.104 044101
[25]W alker R G,Koster R W,Sun C,M off at G,Barger J, Dodson P P,Chapm an F W 2009 Resuscitation 80 773
PACS:82.40.Ck,05.45.–a,89.75.KdDOI:10.7498/aps.66.068201
A fterdepo larlizations induced by w ave pattern in hum an ventricu lar tissue∗
Wang Xiao-Yan Wang Peng Tang Guo-Ning†
(College of Physical Science and Technology,Guangxi Norm al University,Guilin 541004,China)
(Received 10 O ctober 2016;revised m anuscrip t received 27 Novem ber 2016)
Recently,arrhythm ogenic condition has attracted special attention of scientists in the field of diff erent discip lines because sudden cardiac death is often caused by cardiac arrhythm ia.A rrhythm ias can have diff erent underlying causes. But the underlying m echanism of arrhythm ia is not fully understood due to cardiac com p lexity.As is well known, one particular group of arrhythm ias is often associated w ith the afterdepolarizations.So far,afterdepolarizations have been studied mainly in isolated cardiac cells.The question how the afterdepolarization is produced at a tissue level has not been w idely studied yet.In this paper,we use the m odel of hum an heart to study how spiral wave or other wave patterns induces the afterdepolarizations in two-dimensionalmyocardial tissue.We try to obtain the instantaneous spatial distribution of afterdepolarizations by changing the L-type calcium and fast potassium conductance.In order to avoid bringing in afterdepolarizations,the app lied param eters avoid evoking the afterdepolarizations at a single-cell and one-dimensional tissues level.The numerical simu lation results show that spiralwave and other wave patterns can cause the phase II and III early afterdepolarizations,the delayed afterdepolarization,the enhanced autom aticity,the delayed excitation and the delayed enhanced autom aticity to occur.M oreover,we observe the weak oscillation of them embrane potential during the phase Iof action potential.The afterdepolarizations generally occur in the spiral-wave core.They are generated by the phase singularity of spiralwave.The afterpolarizations can also appear in other region of spiralwave pattern.The afterpolarization is characterized by scattered distribution.W hen param eters are appropriately chosen, we observe the outbreaks of diff erent afterpolarizations under the state of spiral wave.The corresponding spatial and tem poral distributions of the early afterdepolarizations,the delayed afterdepolarizations,and the enhanced autom aticity become spiral line distributions,which exhibitsmemory eff ect.It is shown that the outbreaks of afterdepolarizations in the system do not necessarily lead to the breakup of spiral wave.By observing the changes of diff erent ion currents we find that when sodium current exciting cell is very sm all,the weak excitation w ith sm all sodium current can cause the L-type calcium current and the sodium calcium exchange current to increase,and the slow potassium current and rapid potassium current to decrease,leading to the occurrences of various afterdepolarizations.Therefore,increasing sodium current can eff ectively suppress the occurrences of afterdepolarizations.
spiralwave,afterdepolarizations,enhanced automaticity,Ten Tusscher-Noble-Noble-Panfi lov model
10.7498/aps.66.068201
∗国家自然科学基金(批准号:11565005,11365003)资助的课题.
†通信作者.E-m ail:tangguoning@sohu.com
*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.11565005,11365003).
†Corresponding author.E-m ail:tangguoning@sohu.com
——从一道浙江选考生物学试题谈起

