高非线性光纤中受激布里渊散射快光提前及脉冲形变

车永康, 侯尚林, 雷景丽， 王道斌, 李晓晓,

(兰州理工大学 理学院， 甘肃 兰州 730050)

高非线性光纤中受激布里渊散射快光提前及脉冲形变

车永康, 侯尚林*, 雷景丽， 王道斌, 李晓晓,

(兰州理工大学 理学院， 甘肃 兰州 730050)

基于受激布里渊散射三波耦合方程组，应用小信号分析，研究了高非线性光纤的信号光脉冲提前及形变。结果表明，光纤中信号光脉冲的时间提前量在一定范围内随着输入信号光功率和传输距离的增长而近似线性增长，同时脉冲压缩程度加强；在相同条件下，非线性光纤比普通单模光纤的时间提前量更大，在50 m长的高非线性光纤中，信号光能量在50 mW时实现了203 ns的时间提前量和较小的脉冲形变。高非线性光纤的快光提前效率显著提高，脉冲形变显著减小。研究结果对快光的实现和应用具有参考意义。

非线性效应； 受激布里渊散射； 时间提前量； 脉冲压缩

1 引 言

理论上，根据光脉冲的群速度与光的真空速度c的比较，可以把群速度分为快光和慢光：群速度远小于c为“慢光”[1-2]；大于c或成为负值，称为“快光”[3-4]，当群速度为负时，脉冲包络在色散材料中向后传输，因此也称为“后向光”[5]。光速调控技术可以追溯到二十世纪初，Brillouin等[6]理论上预言了群速度可以超过光速。激光器问世以后，物质快慢光现象的实验研究才取得了明显进展[7]。近年来，有关慢光或快光的相关现象引起了学者们的极大兴趣[8]，对色散介质中传播的光脉冲群速度的调控也成为可能[9-10]。但在室温、固体中实现快慢光技术有现实意义。

近年来，光纤中调控光速的研究文献非常多，Boyd的综述性文献[11]做了比较系统的概括。从实际应用的角度，这方面的研究主要基于以下几种技术：受激布里渊散射(SBS)、受激拉曼散射(SRS)、参量放大和光纤布拉格光栅等。光纤中SBS调控光速具有以下优点：与光纤通信系统兼容；调控不受波长限制；控制相互作用的光纤长度和泵浦光功率可以改变延时量或提前量；相互作用发生在室温下，不需要冷却。SBS现已成为光纤中调控光速最现实的技术。但相比于慢光，快光工作于吸收带反常色散区，信号衰减剧烈，时间提前量又受到增益饱和的限制，因此难以长距离实现快光持续存在。

快光技术在光通信、光与物质相互作用、时间隐身、引力波探测等诸多领域有着潜在的应用价值。近年来，学者们对受激布里渊快光技术做了广泛的研究。2004年，Gauthier等[12]率先提出在光纤中利用受激布里渊散射实现快光。随后，Song等[13]在实验中利用光纤的受激布里渊散射效应观察到快光现象，信号时间提前量首次达到10 ns。詹黎等[14]在10 m的单模光纤中通过实验实现了221.2 ns的时间提前量。2013年，Deng等[15]在受激布里渊散射激光环形腔中的高非线性光纤实现了负群速度超快光传输。2016年，詹黎和张亮等[16]运用带有饱和吸收器的单纵模长腔布里渊光纤激光放大器，首次把布里渊诱导快光传输的距离提高到500 m。目前国内外基于SBS快光特性的研究主要致力于提高信号光的时间提前量和解决信号提前伴随的失真，而且研究主要集中在实验验证方面，且对脉冲形变研究较少，对快光发生机制的阐述和对快光特性的理论系统分析的文献较少。

本研究组近年来对光纤中受激布里渊散射快慢光的传输特性展开了研究[17]，在以往研究的基础上，本文阐述了光纤中受激布里渊散射快光的发生机制，研究了普通单模光纤(SMF)和高非线性光纤(HNLF)中信号光时间提前量和脉冲压缩因子随信号光功率和传输距离的关系。高非线性光纤中以较小的信号光功率和传输距离就能获得较大的时间提前量，这样避免了能量过高引起光纤中其他非线性效应而导致脉冲失真。高非线性光纤中更高的快光提前效率可以在很多领域有潜在的应用，如高灵敏度传感、数据同步技术、引力波的探测、时间历史隐身、前沿信息的检测等。

2 受激布里渊散射快光小信号分析

受激布里渊散射的三波耦合方程描述的是泵浦波、斯托克斯波和声波之间的相互作用。当反向传输的泵浦光和斯托克斯光进入光纤后，强光场引起光纤介电常数的周期性变化，产生声波场。声波在介质中激起周期性变化的光栅，对泵浦光进行散射，使斯托克斯光光强指数性增长。入射光在光栅的作用下产生频率下移的斯托克斯光和频率上移的反斯托克斯光，由于反斯托克斯光(泵浦光)的中心频率位于吸收峰内，信号光获得时间提前量而产生快光。

设定斯托克斯光为高斯脉冲波形且光强足够小，泵浦光为连续光谱。在泵浦波、斯托克斯波和声波的线性耦合过程中，斯托克斯光沿着光纤的z方向传输，泵浦波沿着z的反方向传输，声波同样是反向的。考虑光纤中的一维情况，在慢变包络近似的条件下，斯托克斯波、泵浦波、声波的三波耦合方程如下[18-19]：

(1)

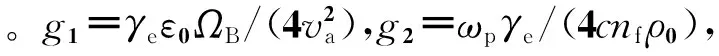
如果以泵浦光作为信号光来分析，其中心频率恰好处于吸收峰的范围内。对应的失谐频率δω=ω-ωp-ΩB为0时，满足快光产生的相位匹配条件ωs=ωp+ΩB。即信号光处于吸收峰，发生反常色散，相折射率负变化，群速度加快。应用小信号分析，由三波耦合方程可以解得增益系数gs、相折射率ns、和群折射率ng如下：

(2)

式中Is表示信号光的强度，δω=ω-ωp+ΩB表示失谐频率，即信号光的中心频率与布里渊吸收谱中心频率的差值，g0=4g1g2/(ηΓB)表示布里渊吸收峰值系数。

提前量ΔT定义为发生SBS与不发生SBS时输出信号波峰值的时间差。群折射率的变化会导致光脉冲群速度的改变，对于群折射率变化量为Δng的光纤介质，可以表示为

(3)

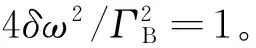
(4)

在布里渊吸收峰峰值处(δω=0)，信号光的时间提前量获得最大值：

(5)

对于半高全宽是τin的高斯型斯托克斯光脉冲，在共振处提前后的信号形状仍然是高斯型，半高全宽是τout，脉冲压缩因子为

(6)

3 数值计算

作为对比，分别对普通标准单模光纤和高非线性光纤作为传输介质，模拟了不同信号光功率、传输距离和输入脉冲宽度对应的信号光时间提前量和脉冲的压缩量的关系曲线。两种光纤的参数如表1所示。

表1 两种光纤参数

3.1 单模光纤中的快光

图1为标准单模光纤中受激布里渊散射快光的时间提前量和压缩因子随信号光功率和传输距离的变化曲线。图1(a)表明在小信号模型下，时间提前量随着信号光功率的增强近似线性增长，增加传输距离也可以获得更大的时间提前量。当光纤长度L=50 m信号光功率Ps=50 mW时，可以得到98 ns的时间提前量。但是实际情况中，时间提前量不能简单地靠提高信号光功率和增加传输距离无限增加。因为吸收饱和的存在，时间提前量在信号光功率达饱和值后反而减小，光速减慢。随着信号光功率的增强，其他的一些非线性效应也会出现，信号波形严重失真。从图1(b)中可以看出，随着信号光功率的增加，信号脉冲被压缩的程度变大，同时信号脉冲的宽度也随着传输距离的增加而变窄，传输距离L=50 m、Ps=50 mW时，脉冲压缩因子是0.52。

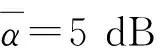
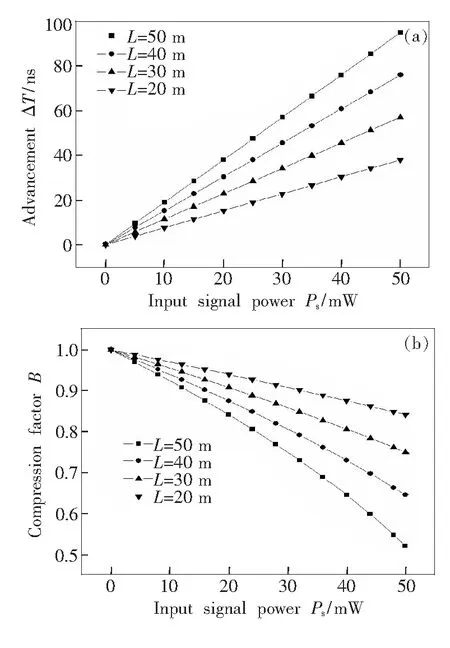
图1 提前时间(a)和压缩因子(b)随信号光功率的变化曲线

Fig.1 Advancement(a) and compression factor(b) as a function of signal power

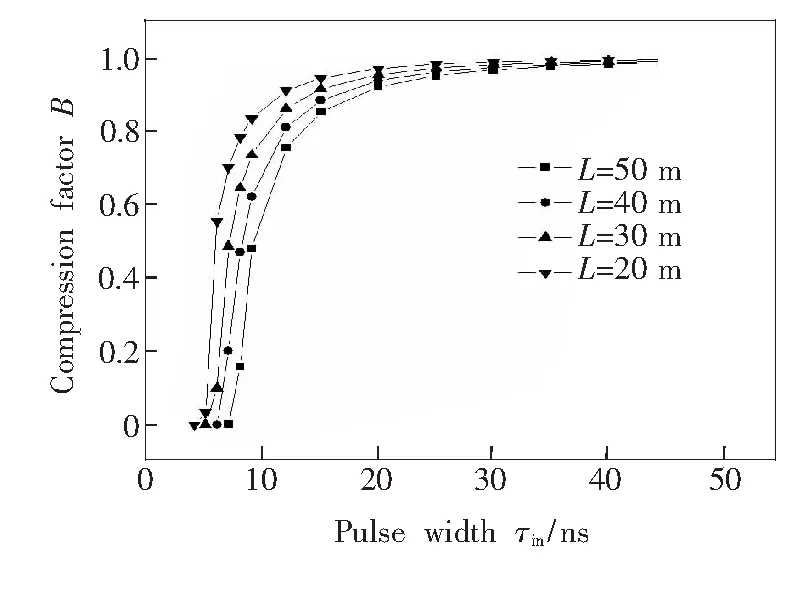
图2 压缩因子随输入脉宽的变化曲线

图3为脉冲信号在50 m标准单模光纤中的传输波形随信号光功率的变化曲线。可以看出随着泵浦功率和传输长度的增加，在获得时间提前量的同时，信号脉冲被压缩。在标准单模光纤中，当传输距离L=50 m、信号光功率Ps=25 mW时，可以获得49 ns的时间提前量，脉冲展宽因子为0.81。

图3 脉冲信号的输出波形

Fig.3 Waveforms of the output signal with different input power

3.2 非线性光纤的快光

图4表示在相同信号光功率和传输距离的前提下，高非线性光纤中受激布里渊散射对应的相对归一化吸收峰曲线以及相折射率和群折射率随频率的变化曲线。从图4可以看出，高非线性光纤由于模场面积小使归一化吸收系数更大，相折射率变化更明显，群折射率变化剧烈。从本质上分析可知，在相同条件下，高非线性光纤可以获得更大的时间提前量。相位的变化量随归一化吸收系数的增加而变大(相位获得剧烈变化)，最大时间提前量在吸收峰峰值中心频率处得到。

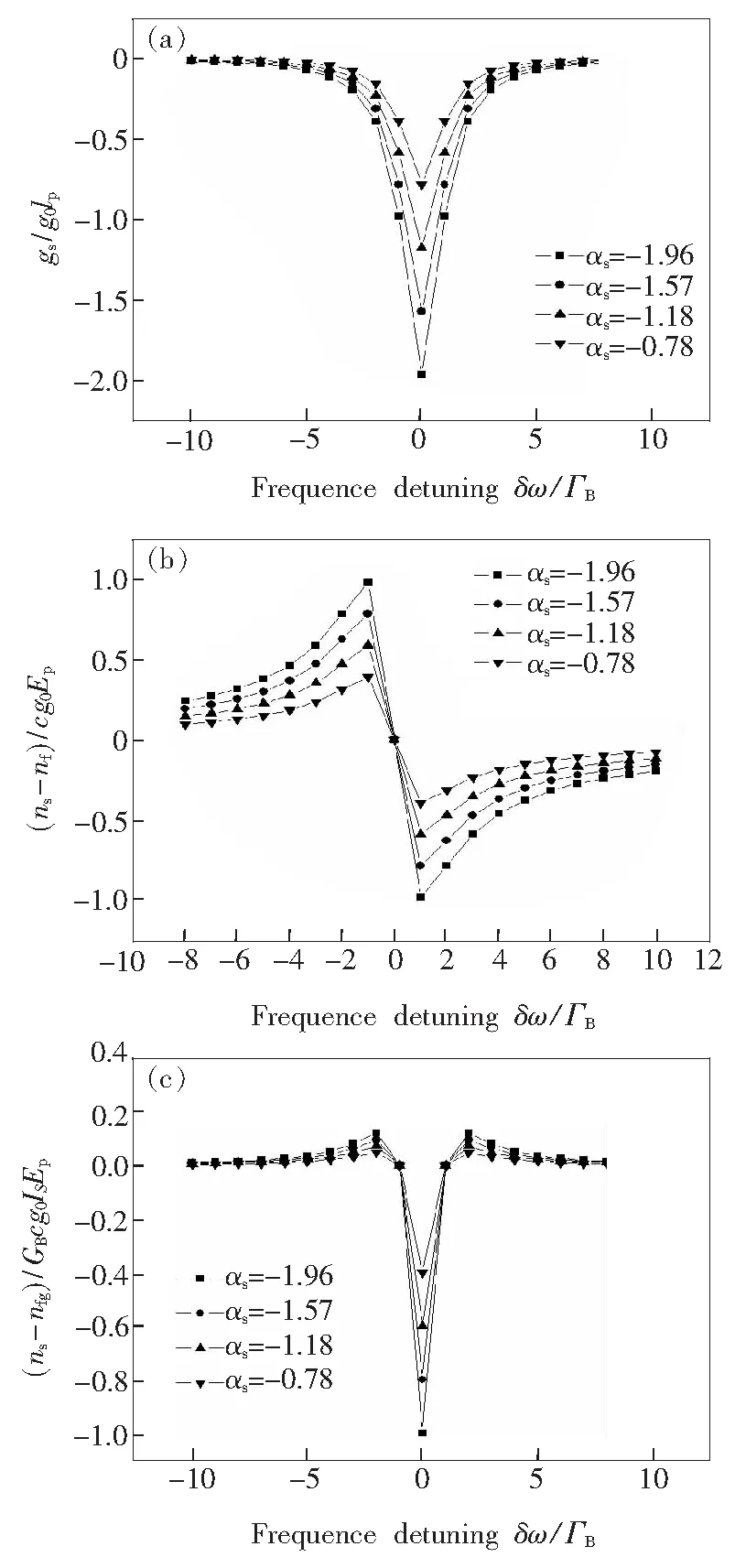
图4 SBS频率共振处的吸收峰(a)、相折射率(b)和群折射率(c)的变化曲线。

Fig.4 Absorption (a)， phase index (b) and group index (c) at the frequency of the SBS resonance， respectively.

图5(a)模拟了高非线性光纤时间提前随信号光功率的变化曲线，由图可知，时间提前量随着信号光功率和传输距离的增加而近似线性增长，当传输距离L=50 m、信号光功率Ps=50 mW时，时间提前量可以达到203 ns。图5(b)对应高非线性光纤中脉冲压缩量随信号光功率的变化曲线，与图1对比可知对于特定传输长度的非线性光纤，与标准单模光纤相比脉冲压缩程度严重。比如在信号光强为20 mW时，传输距离是50 m的标准单模光纤中的压缩因子是0.85，而高非线性光纤中脉冲压缩因子已达到0.48。为较大程度地使信号波形无失真传输，高非线性光纤中信号光的功率需要限制在更小的范围内。

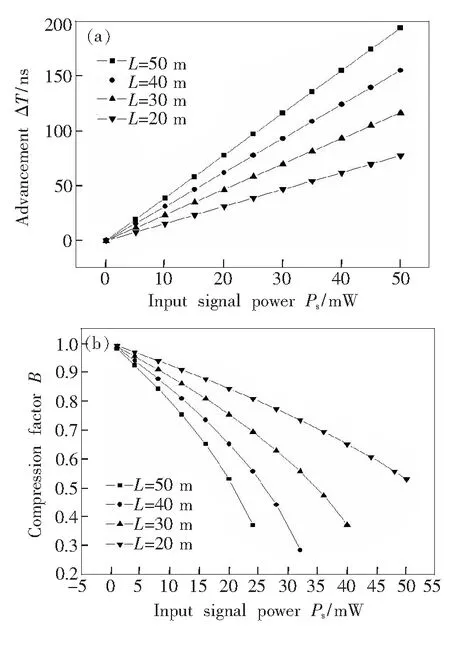
图5 提前时间(a)和压缩因子(b)随信号光功率的变化曲线

Fig.5 Advancement(a) and compression factor(b) as a function of signal power

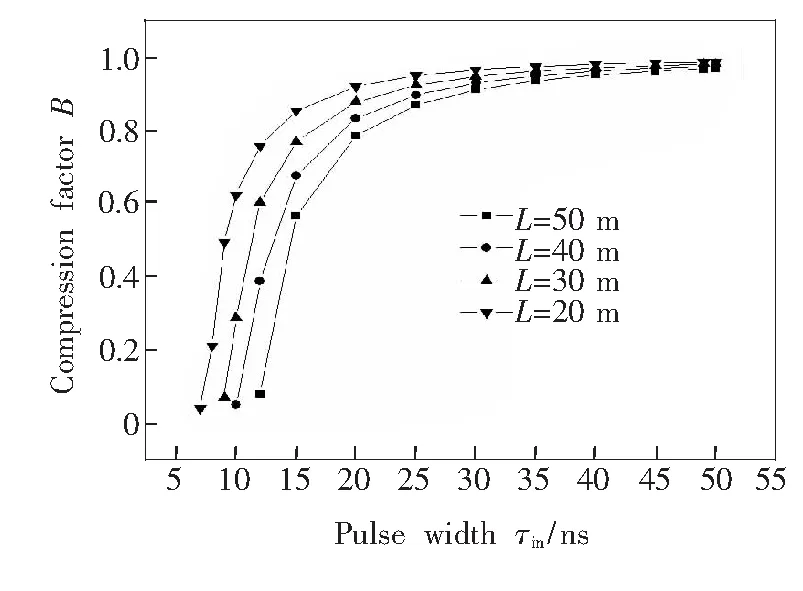
图6 压缩因子随输入脉宽的变化曲线

高非线性光纤中，脉冲的传输波形随信号光强和传输距离的传输波形如图7所示。从图7可以看出：在传输介质距离L=50 m、信号光功率Ps=25 mW时，可以得到98 ns的时间提前量，脉冲压缩因子为0.48。在相同传输长度和信号光功率的条件下，与标准单模光纤相比，信号光获得了更大的时间提前量，与此同时脉冲压缩程度较严重。

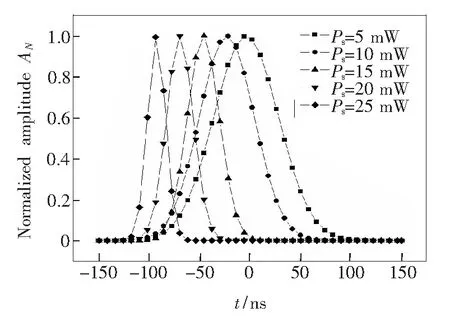
图7 脉冲信号输出波形

Fig.7 Waveforms of the output signal for different input power

3.3 不同光纤中快光特性对比

图8模拟了传输距离为50 m时，两种不同光纤中时间提前量和脉冲压缩因子随信号光功率的关系曲线。从图8(a)中可以看出，在相同信号光功率条件下，高非线性光纤中信号光的时间提前效率明显高于单模光纤。在50 m传输介质中，当信号光功率为50 mW时，高非线性光纤和单模光纤中分别获得203 ns和98 ns的时间提前量。从图8(b)中可以看到，在相同信号光功率的条件下，高非线性光纤中的信号压缩情况更严重。当信号光功率为20 mW时，脉冲压缩因子分别为0.53和0.84。尽管高非线性光纤中脉冲压缩情况较单模光纤严重，但是高非线性光纤可以以较低的信号光功率和较短的传输距离获得理想的时间提前量，这就避免了能量过高引起其他非线性效应使信号脉冲产生畸变，这是标准单模光纤不能比拟的。

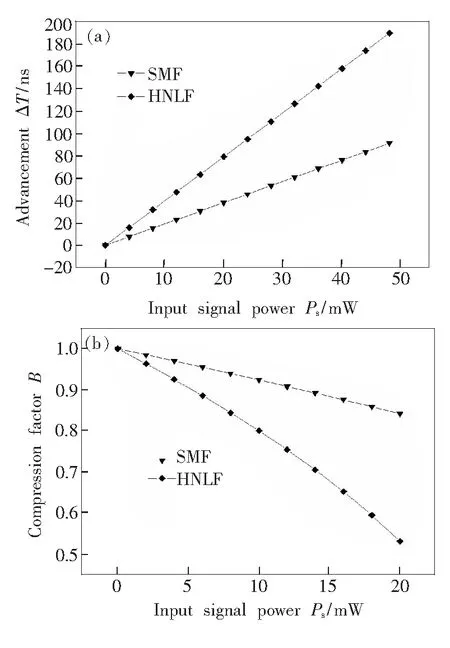
图8 光纤中的时间提前量(a)和脉冲压缩因子(b)的对比曲线

Fig.8 Advancement (a) and compression factor (b) in different fibers

4 结 论

提高信号光功率、增加传输距离和减小输入信号脉冲宽度，都会引起信号光时间提前量的增大，与此同时脉冲压缩情况更严重。当信号光功率超过饱和吸收值后，光速将减慢，光纤中其他非线性效应随着信号光功率增加也表现出来使脉冲畸变，时间提前量并不能简单地靠提高信号光功率和增加传输距离无限增加，所以在单模光纤中仅靠增加信号光功率来获得理想时间提前量是比较困难的。对于高非线性光纤，由于其较小的模场面积而具有丰富的非线性效应，用较小的传输距离和较低的信号光功率能够实现理想的时间提前量，脉冲压缩情况可控。所以高非线性光纤既具有更高效的时间提前效率，又可以最大程度地保持脉冲信号无失真传输，高非线性光纤更适合作为实现快光的传输介质。

[1] HAUL V, HARRIS S E, DUTTON Z,etal.. Light speed reduction to 17 metres per second in an ultracold atomic gas [J].Nature, 1999, 397(6720):594-598.

[2] KASHM M, SAUTENKOV V A, ZIBROV A S,etal.. Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas [J].Phys．Rev．Lett., 1999, 82(26):5229-5232.

[3] CHU S, WONG S. Linear pulse propagation in an absorbing medium [J].Phys．Rev．Lett., 1982, 48(11):738-741.

[4] STENNER M D, GAUTHIER D J, NEIFELD M A. The speed of information in a ‘fast-light’ optical medium [J].Nature, 2003, 425(6959):695-698.

[5] GEHRING G M, SCHWEINSBERG A, BARSI C,etal.. Observation of backward pulse propagation through a medium with a negative group velocity [J].Science, 2006, 312(5775):895-897.

[6] BRILLOUINL.WavePropagationandGroupVelocity[M]. New York: Academic Press, 1960.

[7] FAXVOG F R, CHOW C N Y, BIEBERT,etal.. Measured pulse velocity greater thancin a neon absorption cell [J].Appl．Phys．Lett., 1970, 17(5):192-193.

[8] BOYD R W, GAUTHIER D J. Controlling the velocity of light pulses [J].Science, 2009, 326(5956):1074-1077.

[9] ZHU Z M, GAUTHIER D J, BOYD R W. Stored light in an optical fiberviastimulated Brillouin scattering [J].Science, 2007, 318(5857):1748-1750.

[10] 毛强明, 李长红, 夏铮. 矩形孔光子晶体波导慢光特性 [J]. 光子学报, 2016, 45(2):0223002-1-6. MAO Q M, LI C H, XIA Z. Investigation on slow light properties in rectangular holes photonic crystal waveguide [J].ActaPhoton．Sinica, 2016， 45(2):0223002-1-6. (in Chinese)

[11] BOYD R W. Material slow light and structural slow light: similarities and differences for nonlinear optics [J].J.Opt.Soc.Am. B, 2011, 28(12):A38-A44.

[12] GAUTHIERD J.PhysicsandApplicationsof“Slow”Light[M]. Durham, NC: Duke University, 2004.

[13] SONG K Y, HERREZ M G, THÉVENAZ L. Observation of pulse delaying and advancement in optical fibers using stimulated Brillouin scattering [J].Opt．Express, 2005, 13(1):82-88.

[14] ZHANG L, ZHAN L, QIAN K,etal.. Superluminal propagation at negative group velocity in optical fibers based on Brillouin lasing oscillation [J].Phys．Rev．Lett., 2011, 107(9):093903-1-5.

[15] DENG D H, GAO W Q, LIAO M S,etal.. Negative group velocity propagation in a highly nonlinear fiber embedded in a stimulated Brillouin scattering laser ring cavity [J].Appl．Phys．Lett., 2013, 103(25):251110-1-4.

[16] ZHAN L, ZHANG L, QIN M L,etal.. Long-distance superluminal propagation in optical fibers: recent advances [J].SPIE, 2016, 9763:97630V-1-7.

[17] HOU S L, WEN B, LI H B,etal.. Effects of SBS slow light on super-Gaussian pulses in fibers [J].Opt．Commun., 2014, 323:13-18.

[18] KUMAR S, DEEN M J.Nonlineareffectsinfibers[M]. KUMAR S, DEEN M J.FiberOpticCommunications:FundamentalsandApplications. Chichester: John Wiley & Sons, 2014:419-495.

[19] 侯尚林, 荆志强, 刘延君, 等. 光子晶体光纤中基于受激布里渊散射实现快光的数值模拟研究 [J]. 发光学报, 2016, 37(3):358-365. HOU S L, JING Z Q, LIU Y J,etal.. Numerical simulation of the realization of fast light based on stimulated scattering in photonic crystal fiber [J].Chin.J.Lumin., 2016, 37(3):358-365. (in Chinese)

车永康(1990-)，男，河北衡水人，硕士研究生，2014年于燕山大学获得学士学位，主要从事光纤受激布里渊散射快慢光器件和传感的研究。

E-mail: 1344660440@qq.com侯尚林(1970-)，男，甘肃天水人，博士，教授，2008年于北京邮电大学获得博士学位，主要从事光纤通信器件和传感的研究。

E-mail: houshanglin@163.com

Time Advancement and Pulse Distort of Stimulated Brillouin Scattering Fast Light High Nonlinear Optical Fibers

CHE Yong-kang, HOU Shang-lin*, LEI Jing-li, WANG Dao-bin, LI Xiao-xiao

(SchoolofScience,LanzhouUniversityofTechnology,Lanzhou730050,China) *CorrespondingAuthor,E-mail:houshanglin@163.com

Based on the three coupled wave equations of stimulated Brillouin scattering and under the condition of small-signal model, the time advancement and pulse distort of fast light in high nonlinear optical fiber were investigated. The results indicate that the time advancement linearly increases and pulse compression becomes larger with the increasing of the input signal power and the transmission distance in optical fiber. Under the same condition, the time advancement occurred in high nonlinear optical fiber is larger than that in single mode fibers, and the maximum advancement of 203 ns as well as small pulse distort are achieved in high nonlinear fiber at the signal power of 50 mW and the fiber length of 50 m. The efficiency of time advancement of fast light in high nonlinear fiber is significantly improved and the pulse deformation is obviously decreased. The research results provide reference for the implementation and application of fast light.

nonlinear effect; stimulated Brillouin scattering; time advancement; pulse compression

1000-7032(2017)08-1083-07

2016-12-26；

2017-02-16

国家自然科学基金(61665005，61167005，61367007)资助项目 Supported by National Natural Science Foundation of China(61665005，61167005，61367007)

TN929.11

A

10.3788/fgxb20173808.1083