基于阿克曼原理的舵机与差速电机协同控制算法的研究与应用
周润发,杨 琦,汪元礼,李 丹,卫军帅
(1.安徽工业大学 电气与信息工程学院;2.安徽工业大学 工程实践与创新教育中心;3.安徽工业大学 学生工作部,安徽 马鞍山 243002)
基于阿克曼原理的舵机与差速电机协同控制算法的研究与应用
周润发1,杨 琦2,汪元礼1,李 丹1,卫军帅3
(1.安徽工业大学 电气与信息工程学院;2.安徽工业大学 工程实践与创新教育中心;3.安徽工业大学 学生工作部,安徽 马鞍山 243002)
本文依据阿克曼原理分析了智能车C车模转弯时前轴舵机角度与后轴电机差速之间的关系,提出了提出改进式的PID控制伺服舵机转角与双电机差速协同控制的优化算法,通过智能车在转弯时速度和稳定性的实验数据验证了该算法正确性.
阿克曼原理;差速控制;PID控制
随着最些年来汽车工业不断发展和自动控制技术的不断升级,智能汽车特别是无人驾驶汽车是发展的重要方向之一,如何使智能汽车高效、稳定地运行,特别是转弯过程成为大家争相研究的课题.本文依据阿克曼原理,对恩智浦智能C车模转弯时前轮的转向与后轮差速的协同配合进行研究,提出改进的PID控制算法,使车模能够更好地转向.
1 理论模型
阿克曼原理是在不考虑汽车质心侧偏、汽车行驶过程中的侧向力、横摆角和极端恶劣的路况下,车辆无论是直行还是在拐弯时,如果每个车轮的运动轨迹都可以完全符合它的自然运动轨迹,那么就可以保证轮胎与地面间处于纯滚动而无滑移现象.两轴车在转向行驶过程中,全部车轮须绕一个瞬时中心点(转向中心)做圆周滚动,而且前内轮与前外轮的转角应满足一定的关系,这样才可以保证轮胎与地面间处于纯滚动而无滑移现象,从而保证车辆在行驶时是相对可控的.
恩智浦智能车竞赛中的C型车模的二轴车机械结构决定了后轴两轮与转向中心在一条直线上,由于后轴两轮距离与阿克曼原理的转向中心的距离不等,所以只有在一段很短的时间内左右两轮的转速不同,才能绕一个转向中心做圆周滚动,进而有效地保证整车的稳定性.
我们可以借助单片机高频特性对整车的运动状态进行分析,在每个微分时间段内,不断地通过前轴舵机角度和对输出PMW波对后轴电机之间的转速进行调整,保证整车的配合,从而使车辆满足阿克曼原理,进而保证轮胎与地面间处于纯滚动而无滑移,使之过弯平稳,过程可控.
2 数学模型
2.1 后轮两轮的差速关系
根据阿克曼转向的几何要求,恩智浦智能车C型车模所全部车轮就都必须绕一个转向中心点做圆周滚动,如图1所示,其中W为后轮两轮的轮距,L为前后轮的间距,以及如图示的各点与转向中心的角度,入弯之后的车模后轮里面的转速为V_in,入弯之后后轮外面的转速为V_out.
根据物体的圆周运动规律公式V=ω×R,由于单片机的一个工作周期相对于整个运动过程非常短,设单片机的一个完整工作周期时长为dt,那么ω=dθ/dt,则导出速度公式V=dθ×R/dt.而且,R_in=R-W/2,R_out=R+W/2,如图2所示,根据阿克曼原理,车辆的后轮必须绕同一个转向中心做圆周滚动得知,此时就要满足那么后面两个轮子的角速度是相同,即可以推导出

内轮产生的移动dx_in=R_in×dθ/2π,外轮产生的偏移 dx_out=R_out×dθ/2π, 由 于 V_in= dx_in/dt, V_out=dx_out/dt,进而推导出过弯时的差速公式:
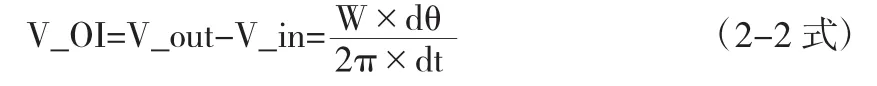
其中的W为常量,dt为常量是单片机完整工作一个周期的时间.为进一步分析dθ与理想位置(中线)的关系,改进PID控制算法,下面我们对dθ进行的探讨.
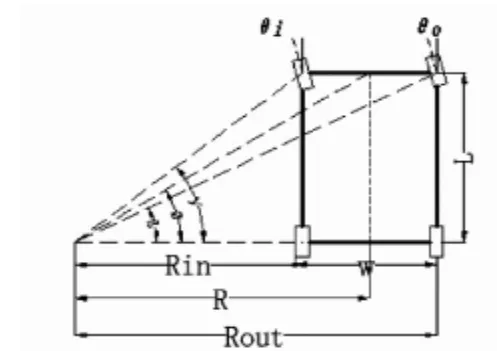
图1
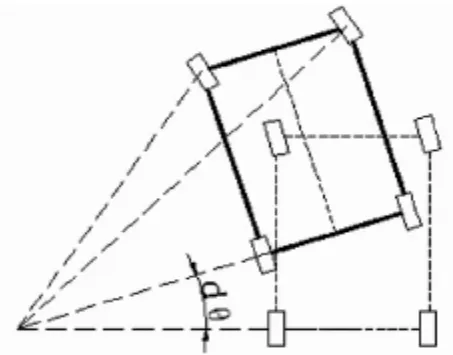
图2
2.2 过弯的曲率与改变的角度dθ的关系
赛道提取算法是:车模上的传感器(摄像头)从车的近处向远处扫描合理的区间内跳变点(即边沿追踪滤波算法),并将每一行的跳变点存入一个数组,因为车处于赛道之上,我们可以找到多行跳变点,不会出现完全丢线的情况.我们利用Δt时刻采集到的跳变点y1、y2,与Δ(t+1)时刻的跳变点y1'、y2'进行分析处理.利用斜率公式:tanθ=(y2-y1)/ (x2-x1)=Δy/Δx.其中Δx相当于传感器(摄像头)当前采集行行距D,y为跳变点的坐标位置.抽象出的赛道信息如图3所示.

其中K为曲率,ds为微分弧长,dθ为偏移角度,dx在图3中的体现为竖直方向的增加量.
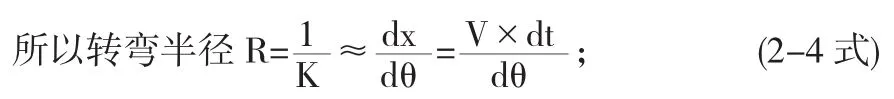
dθ如图3标注所示,为y1与y1'相对于中心的偏移角度,也近似是直线y1y2与直线y1'y2'交线的夹角,由于在角度很小时存在tan(θ)≈θ,即可以得出
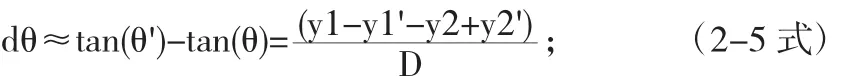
我们带入上面的(2-2式),得到差速方程

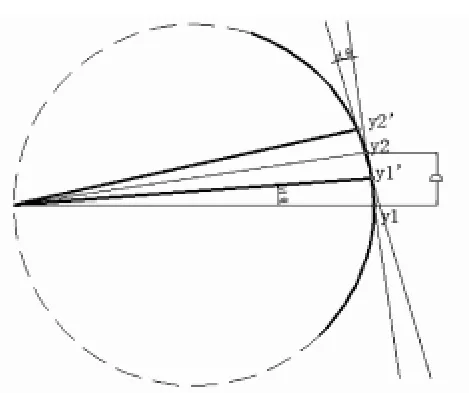
图3

图4
2.3 将差速进行自适应分配
为将差速分配给两边电机,我们设外轮转速V_out= V+A×V_OI,内轮转速V_in=V-(1-A)×V_OI,其中V为速度设定值,A为差速自适应分配比例因子,由2-1式,得

结合(2-4式),(2-5式)与(2-6式),我们可以看出差速自适应分配比例因子主要由dθ所决定.而式中的(y1-y2)就是传感器(摄像头)在一个时刻从赛道提取出的路径误差,那么(y1-y2+y2'-y1')也就是经过dt后,同行路径误差之差.我们将其作为对系统输出误差的反馈,通过反馈来调整差速自适应分配比例因子以及差速大小,从而达到A可以通过误差参数dθ进行自我调整.
2.4 舵机与差速的协同配合
通过舵机打角与电机差速的配合,从而保证舵机所打角度的转向中心与电机差速的转向中心一致,控制舵机转角的PID控制程序为
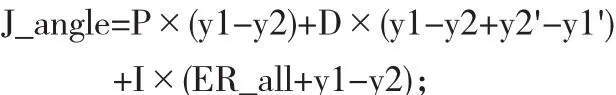
其中J_angle为舵机所打的角度,P、I、D为PID控制的调整参数,ER_all为误差的累积.
3 实验数据及其分析
我们选取飞思卡尔K60单片机作为车模的控制核心,传感器采用摄像头OV7725,欧姆龙系列200P/R编码器对两边电机测速,对电机转速进行了闭环控制,并通过蓝牙模块将车辆在赛道中的位置情况实时传输给上位机.
车模电机主要技术参数如下:额定工作电压7.2V;最大工作电压9.6V;最大效率点:电流0.679A、转速13050转;最大功率点:电流1.537A、转速8044转;堵转电流2.916A,马达到后轮的传动比为7.46.
测试赛道环境:赛道路面采用专用白色PVC耐磨塑胶基板制作.跑道表面为白色,赛道两边有黑色线,黑线宽25mm±5,沿着赛道边缘粘贴,赛道宽度为45cm.(赛道中间坐标位置我们设为40),如图4所示.
车辆过弯偏移赛道的数据记录如下:如图5所示的是差速控制时车模偏移赛道中线情况曲线,如图6所示的是无差速控制时车模偏移赛道中线情况曲线,我们可以从图中看出,在无差速控制时车模偏移赛道中线的范围在21—68之间,在差速控制时车模偏移赛道中线的范围在28—58之间,由此看出,在差速控制算法下车模偏移赛道理想中线的最大位置有较大幅度减小,增强了车模过弯的稳定性,与此同时,车模从偏移到回正的时间也将相应减少.我们测量车速时也发现,未加差速控制时车模过弯速度平均为1.9m/s,加入差速控制后平均车速提升为2.3m/s,速度提升超过20%.
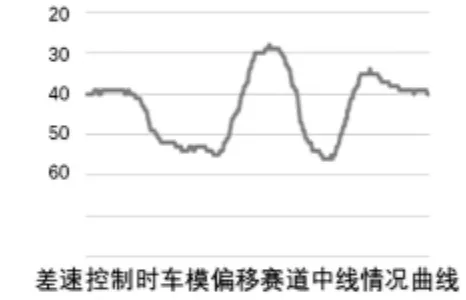
图5
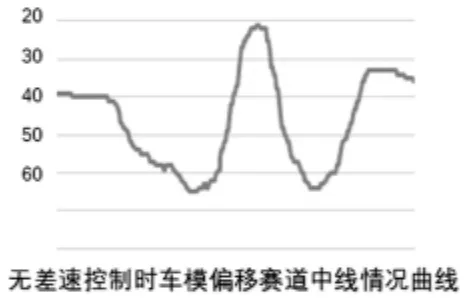
图6
由此可见采用基于阿克曼原理的舵机与差速电机协同控制算法能够使过弯性能得到明显提升.
4 结果与结论
通过将阿克曼转向原理运用于C车车模过弯过程分析,在单片机控制C车模时的应用进行推导,提出差速分配比例因子,得出微分情况下阿克曼转向原理的改进式PID控制伺服舵机转角与双电机差速控制的优化算法,使舵机打角的阿克曼转向中心与电机差速的转向中心相一致,从而在车模过弯过程舵机打角与电机差速更好地配合,对改进智能车的过弯性能以及现代电动汽车的发展研究具有实际意义.
〔1〕卓晴,黄开胜.学做智能车[M].北京:北京航空航天出版社,2007.3.
〔2〕李科浇,赫玉莹,范恒超.后轮双电机差速与前轮转向协调控制在智能车模上的应用[J].科学与财富,2014(4):46-47.
〔3〕姜明国,陆波.阿克曼原理与矩形化转向梯形设计[J].汽车技术,1994(5):16-19.
〔4〕杨其华,张乃标.双电机独立驱动电动汽车的电子差速自调节功能的分析研究[J].北京汽车,2008(5):28-37.
〔5〕许晓飞,夏培容.智能车速度的模糊控制最优循迹策略研究[J].北京信息科技大学学报(自然科学版),2009,24(3): 85-86.
TP273
A
1673-260X(2017)07-0014-02
2017-04-18
安徽省大学生创新创业训练计划项目(201610360340);安徽省大学生创业实验室建设计划项目(2015ckjh010);安徽省思想政治教育改革计划项目(szzgjh1-2-2016-5);安徽工业大学校企合作实践教育基地项目(2012-5)

