考虑界面效应的钢-混凝土组合结构有限元模拟方法
范 亮,李 笑,何 骏
(1.重庆交通大学 土木工程学院,重庆 400074;2.浙江省交通规划设计研究院,浙江 杭州 310006)
考虑界面效应的钢-混凝土组合结构有限元模拟方法
范 亮1,李 笑1,何 骏2
(1.重庆交通大学 土木工程学院,重庆 400074;2.浙江省交通规划设计研究院,浙江 杭州 310006)
鉴于钢-混凝土接触界面剪切力传递问题的复杂性,当前对钢-混凝土组合结构有限元模拟方法多样,但大部分或过于复杂技术难度大,或过于经验化需要依赖大量的试验结果确定参数。考虑实用性和精确性相结合的理念,提出一种采用特定超弹性界面虚拟单元的钢箱混凝土组合结构有限元模拟方法,同时该方法建议混凝土采用混凝土塑性损伤模型。将该方法应用于某组合结构剪力键推出试验模拟中,对其力学性能及界面剪切力的发展全过程进行数值模拟。结果表明该界面模拟方法使用方便、结果可靠,适用于钢箱混凝土组合结构考虑界面黏结滑移效应的有限元模拟中。
桥梁工程;钢-混凝土组合结构;有限元模拟;黏结滑移;推出试验
0 引 言
钢-混凝土组合结构近年来发展较为迅速,广泛运用于桥梁及建筑等领域[1]。由于组合结构本身特点,钢与混凝土、连接件与混凝土之间界面剪切力传递问题不容忽视,国内外学者对此进行了大量实验研究。主要通过推出试验结果获得相关参数,进而得到承载力计算公式,但试验周期长,费用高[2],且对试验现象的观察记录存在诸多困难,而有限元仿真分析则能对模型结构受力全过程进行观察记录,能够较为方便的获得数据。此外,通过实验研究与有限元仿真分析相结合,既可以验证试验数据的准确性,又能为探索合理的建模方式提供依据。钢-混凝土组合结构的有限元模型主要有两种[3],分别为TBM(traditional beam model)传统梁模型和SLM(slip beam model)滑移梁模型。前者将混凝土翼板与钢梁视为共同工作,而不考虑抗剪连接件的变形,组合梁截面符合平截面假定,后者为工程中的简化模型,该模型考虑引入界面滑移函数来模拟钢梁与混凝土交界面处的滑移,该函数所涉及参数可通过推出实验结果确定。损伤力学理论能同时考虑材料初始微裂缝的存在情况以及受力过程中由于损伤积累而导致的应变软化[4],混凝土塑性损伤模型理论能较好地处理钢-混组合结构中混凝土结构破坏前的应力集中问题,且对混凝土应力下降段模拟情况较好。笔者借助ABAQUS有限元软件,提出一种基于混凝土损伤塑性模型理论,同时采用虚拟界面单元模拟钢与混凝土间的界面黏结滑移效应的模拟方法,并对某钢-混凝土组合结构剪力连接件的受力性能以及界面剪切力的发展过程进行了分析。
1 混凝土损伤塑性模型理论
混凝土材料力学行为较为复杂,目前尚未出现公认的可以完全描述混凝土材料本构关系的模型理论。研究表明[4]混凝土损伤塑性模型可以较为精确地模拟单轴受压、单轴受拉、双轴受压以及双轴受拉状态下混凝土材料的力学性能。混凝土在承受外荷载之前就存在微孔洞,这种微缺陷叫做“损伤”。建立合理的混凝土损伤模型是对混凝土结构进行损伤评估的关键问题之一[5]。混凝土的非线性应力-应变特性是由微裂缝的产生和集结引起的,因此,塑性理论并不能反映材料的真实本构特性,而连续介质损伤力学理论为该问题提供了新的理论基础。混凝土损伤塑性模型采用各向同性弹性损伤结合各向塑性受拉和受压来模拟材料非线性本构关系。该模型适用于任意荷载作用情况,同时考虑损伤引起的弹性刚度的退化以及循环荷载作用下的刚度恢复情况[6],有限元法模拟混凝土受力状态主要考虑以下4个因素:
1.1 应变率表达式
应变率可分解为弹性和塑性两部分,其表达式为
ε=εel+εpl
(1)
式中:ε为总应变率;εel为应变率的弹性部分;εpl为应变率的塑性部分。
1.2 本构关系
本构关系主要是弹性损伤关系,可表示为
(2)
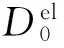
1.3 屈服条件
该模型用有效应力表示的屈服函数的形式为
(3)

(4)
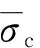
1.4 流动法则
塑性损伤模型采用非相关联塑性流动法则:
(5)
流动能G为Drucker-Prager双曲线函数:
(6)
式中:μ为偏心率,表征了函数趋近渐近线的速率(当μ=0时,G趋向于1条直线);σt0为失效时材料单轴拉应力;φ为高侧限压力条件下的p-q面中膨胀角[4]。
2 钢-混凝土界面模拟
界面问题一直是钢-混凝土组合结构中的核心问题,如果该界面发生过较大滑移,组合结构就会在小于设计强度时发生破坏或过大变形[7]。因此对该界面的模拟是这种结构进行有限元模拟分析的关键。目前,针对组合结构剪力键推出试验的有限元分析主要有两种模式,一种是考虑钢与混凝土的弹塑性,忽略界面效应,另一种是引入联结二者的黏结单元。现有试验研究结果表明:钢材与混凝土的界面性能不仅与二者的材性有关,还受钢与混凝土表面的光滑程度、荷载性能等因素的影响。该界面效应类似于光圆钢筋与混凝土间的界面效应[8],由以下3部分组成:①化学胶结力:水泥凝胶体与钢板间存在值较小的胶结强度;②机械咬合力:由钢板表面的凹凸不平造成的与混凝土间的挤压力,数值取决于钢板表面的粗糙程度;③摩擦力:钢板与混凝土间发生相对滑动后残余的摩擦力,数值大小与接触面所受法向力和摩擦因数成正比[9]。
弹簧单元模型是界面模拟时采用的一种简化模型。文献[7]引入钢板与混凝土接触面上的虚拟连接弹簧连接单元模拟钢与混凝土的黏结滑移情况,该弹簧通过弹簧单元的实常数F-D(受力-变形)曲线的定义确定弹簧的受力性质。具有以下特点:① 弹簧单元有两个结点,不进行材料属性定义,用荷载-滑移曲线定义弹簧单元特性;②F-D曲线用第二象限到第一象限的一系列点构成的折线来定义;③ 原点斜率恒为正值,其余各折线的斜率可以为正或负;④ 在使用二维和三维弹簧单元时两个结点之间的距离不能为0;⑤ 将三维弹簧退化为一维弹簧时结点可以重合。弹簧单元的实常数F-D曲线的定义依赖于推出实验结果,由于需要确定的参数较多,其精确性及通用性较差。
文献[10]提出了采用无厚度黏聚区域模型,模拟钢板与混凝土板以及栓钉与混凝土之间的界面滑动与脱离。该模型中界面黏聚力被克服前无相对滑移,随着荷载增大,当界面剪应力大于黏聚力时,发生相对滑移,当剪应力超过界面抗拉强度时,连接界面沿法向起裂并张开扩展。黏聚区模型中界面单元基于弱化混凝土本构理论,采用了多折线模型材料本构,并利用ABAQUS的二次开发功能中的UEL接口编译了多折线模式界面单元子程序,该方法应用较为复杂,在实际的有限元模拟中有一定局限性。
基于以上研究现状,笔者考虑到模型中钢箱及钢板肋与混凝土之间的界面剪切力作用[11],采用了1层超弹性材料的界面单元与ABAQUS中的束缚约束相结合模拟界面效应,用界面单元的剪切变形模拟剪力作用下的界面相对滑移。界面名义厚度采用2 mm,该数值选择时考虑到既能反映界面受剪后的变形情况,又不对结构产生尺寸效应影响。模型中的超弹性材料具有以下属性[12]:材料行为是弹性、各向同性的;考虑钢混界面的剪切力的几何非线性效应;材料本身是接近不可压缩的,泊松比ν>0.475。在模型中,由于界面黏结滑移本构特性与混凝土强度、钢材表面性状及施工时混凝土的浇筑方向等多种因素有关,因此,该超弹性材料的主要参数仍依靠试验确定。参照弹簧单元模型中F-D曲线形式,笔者建议方程基本形式为
(7)
式中:A1,t0取值与混凝土强度、钢材表面性状等因素相关,y0取值表征了界面发生相对滑移前的那部分作用效应,该值大小与界面化学胶结力、机械咬合力、静摩擦力大小有关。
ABAQUS束缚约束用于模拟被束缚在一起的两对立面(主控面和从属面)间的力学行为,此约束的效果为:使从属面上的节点与主控面最近的点位移一致。在界面单元与外包混凝土之间、界面单元与钢板之间设置该类型约束,见图1,可避免加载过程中单元计算的不连续性[13]。该方法在计算界面出现黏结滑移时可以提高计算速度,简化模型,但不适用于出现界面掀起时的情况。

图1 界面模拟示意Fig.1 Interface simulation diagram
3 模拟实例
为了对比验证该方法的模拟效果,将该方法运用于某组合结构剪力键的推出试验有限元模拟。
3.1 剪力键推出实验简介
剪力连接件是随着组合结构的应用发展而来的,其作用是将钢与混凝土组合成一个整体而共同工作。组合结构连接键有多种形式[10],文中剪力键为开孔钢板连接件,见图2~图4,具体试验尺寸参数见表1[14]。试验中各试件的混凝土标号均为C30,钢板采用Q235钢材,钢筋均为HRB335,剪力键的开孔直径均为30mm,加载方向为由下往上,通过在试件钢箱与混凝土界面不同高度位置测量的电子百分表测得的数据并通过修正,可以准确得到推出试件的荷载-滑移曲线。

图2 钢箱构造Fig.2 Steel box structure diagram

图3 位移计布置Fig.3 Layout of displacement meter
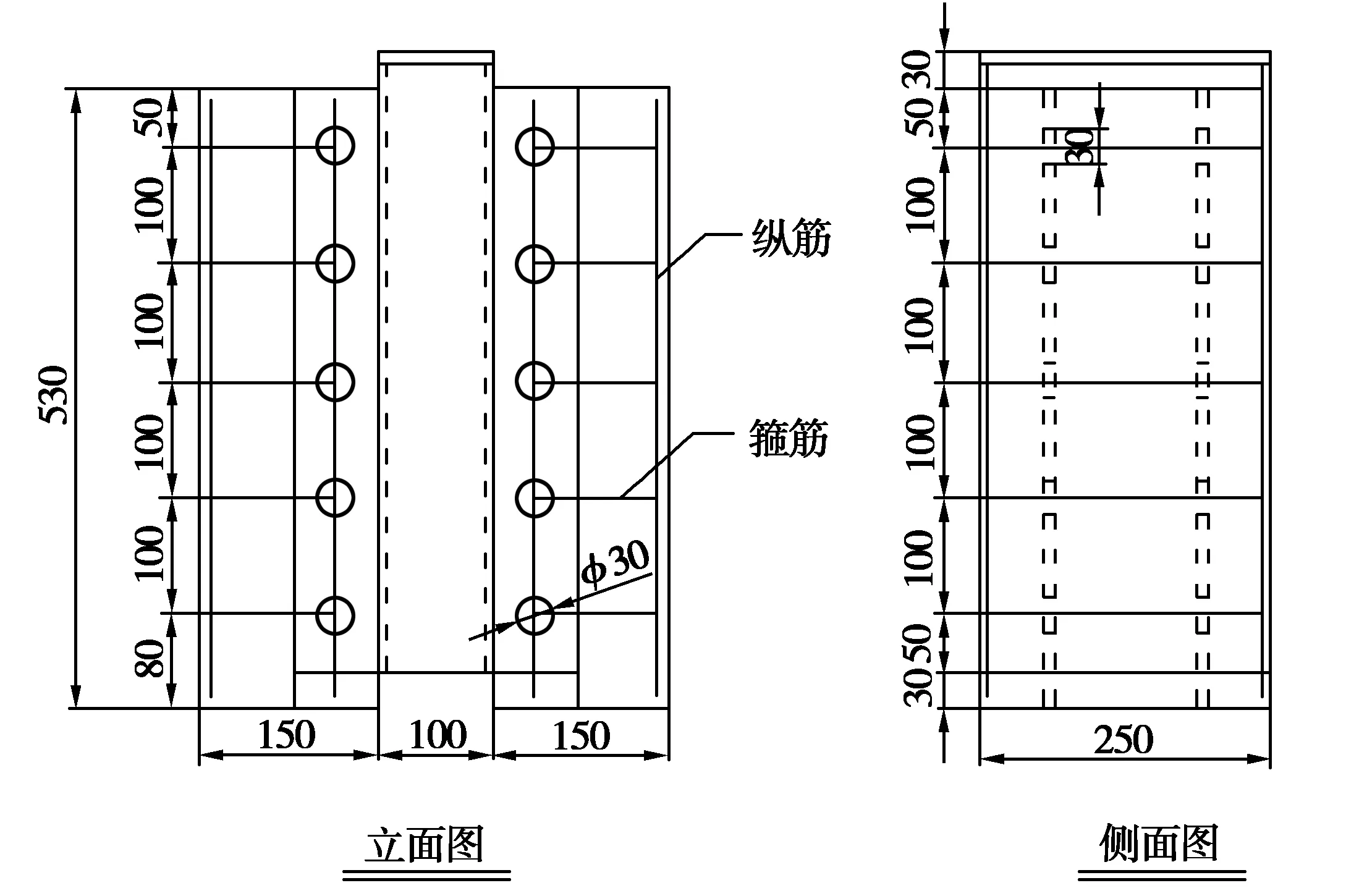
图4 B5试件构造(单位/mm)Fig.4 Structure diagram of specimen B5

Table 1 Main parameters of the tested specimen mm
3.2 有限元模型
利用ABAQUS有限元软件,建立对应的剪力键推出试验试件模型,主要过程如下:
3.2.1 单元类型选择及网格划分
1)单元类型
根据推出试验实际几何尺寸建立各个部件的几何模型,主要部件有:混凝土、混凝土榫、箍筋、纵筋、开孔钢板和虚拟界面,为了顺利解决大变形和多种非线性问题,除纵筋以外的各部件均采用8节点六面体减缩积分单元(C3D8R)。该单元为8节点三维实体单元,每个节点有8个自由度,单元共有24个自由度,且单元的边是直线,边与边相交是直角,任何边上节点都位于该边的中点上。
2)网格划分
由于单元形状会在很大程度上影响非线性分析的结果,在进行单元网格划分时应保证单元形状较为规则,减少畸形单元出现。单元尺寸确定遵循能够反映应力集中区域的应力梯度、细化接触面的单元和尽量降低计算成本的原则。模型中主要部件的有限元模型建立完成后,如图5~图6。

图5 钢箱的网格划分Fig.5 Meshing of steel box

图6 界面单元的网格划分Fig.6 Meshing of interface element
3.2.2 模型接触问题及材料属性定义
1)模型接触问题
本模型中各个部件间的接触情况主要有:混凝土榫与贯穿钢筋间的接触、孔内混凝土与钢板开孔孔壁间的接触、钢板与混凝土间的接触。文中理论模型中采用了以下几种接触类型:束缚约束(tie)、无黏结无摩擦接触、嵌入约束。
2)材料属性及边界条件
根据GB 50010—2010《混凝土结构设计规范》中混凝土的多轴强度及本构关系,参考实验得到单轴受压应力应变结果得出模型中C30混凝土应力应变关系及损伤因子[15]等数据,将其输入到ABAQUS中,以近似分析混凝土结构的材料非线性。笔者对于模型中型钢和钢筋材料,应力应变曲线均采用双折线理想弹塑性模型,界面单元采用超弹性材料。ABAQUS用应变势能来表达超弹性材料的应力应变关系[12]。超弹性材料参数基于上文的基本方程形式,遵循有限元计算结果与推出试验结果一致原则,试算得到界面超弹性材料的主要参数A1、t0、y0取值分别为-3.67、2.11、6.32,进而得到适用于本次试验条件下钢-混凝土结合界面虚拟超弹性材料名义应力应变曲线(图7)及对应的方程。
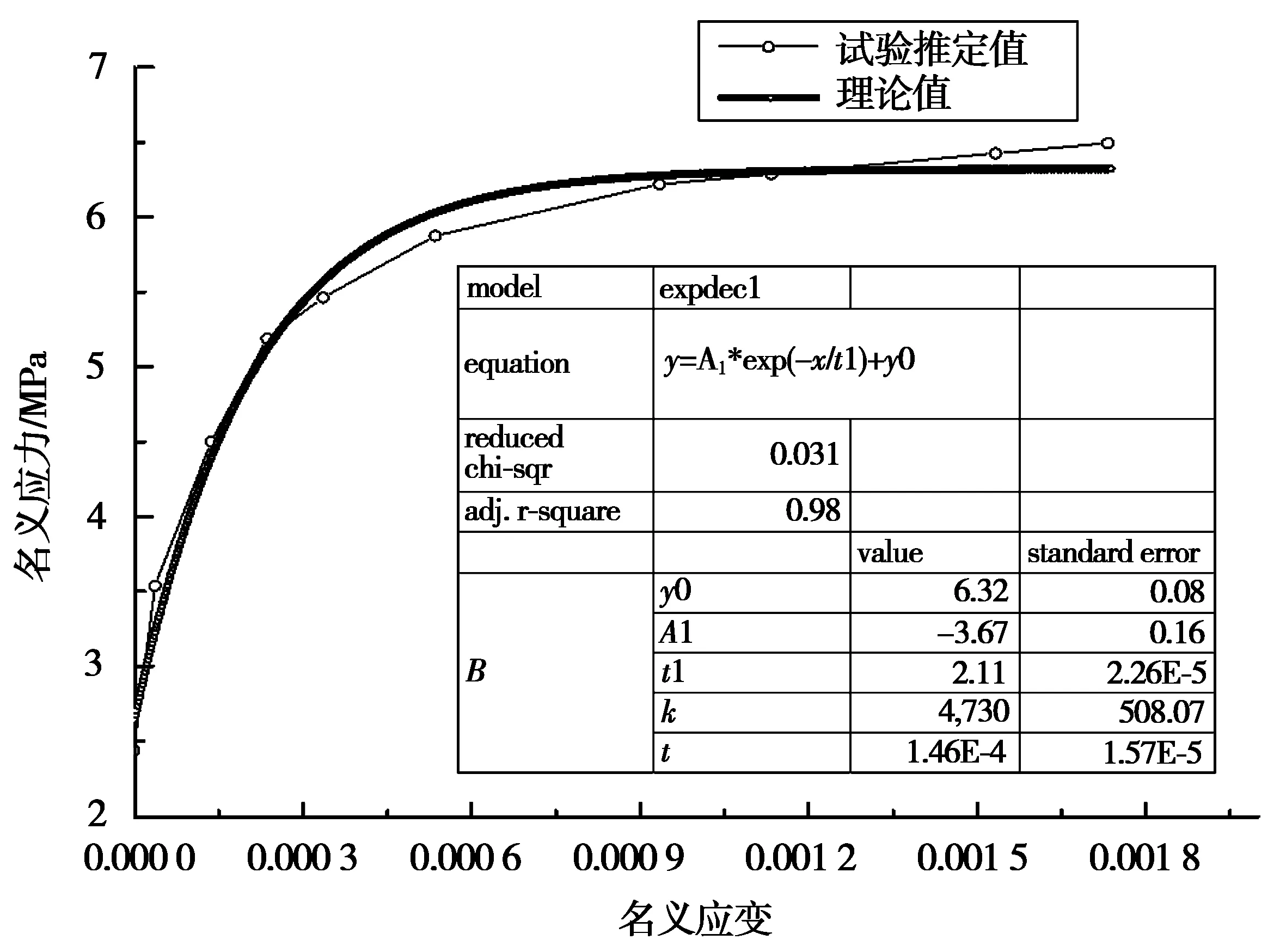
图7 界面单元材料特性Fig.7 Interface element material properties
当名义应力y≤2.65 MPa时,名义应变x值为0,当y≥2.65 MPa时,满足下式关系:
(7)
模型采用了外包混凝土底面所有节点固结的边界条件,与试验底部加载相符。
3.3 对比验证
3.3.1 破坏现象对比
模型求解完成后,可得到如下结论:
1)如图8,可知钢箱与混凝土黏结界面以及外包混凝土几乎完全破坏;由图9可知,混凝土榫损伤较严重,与试验结果(图10~图11)吻合较好。

图8 外包混凝土的最终损伤情况Fig.8 Final damage of covering concrete

图9 混凝土榫的最终损伤情况Fig.9 Final damage of concrete tenon

图10 外包混凝土解剖图Fig.10 Anatomy of the covering concrete

图11 界面处混凝土解剖图Fig.11 Anatomy of the concrete of the interface
2)贯穿钢筋的竖向位移如图12,箍筋竖向位移向上为正,由于肋板孔洞及混凝土榫对贯穿箍筋的作用,箍筋与混凝土榫及肋板交界处出现反弯点,该处变形值也较小,与实际相符(图13)。
3)钢箱的Mises应力如图14,钢箱在肋板孔洞处应力较大,其他部位均未达到屈服,与试验结果吻合(图14),说明钢箱的模拟符合要求。
3.3.2 荷载-滑移曲线对比
支撑节点约束反力和钢箱与混凝土对应节点位置计算位移差的关系即为模型荷载-滑移计算曲线,将之与与实测荷载-滑移曲线进行对比,如图15~图17。由图可知,计算模型的荷载-滑移曲线与实测曲线在弹性阶段基本吻合,极限承载力计算值与试验值相差10%以内,说明有限元仿真分析具有足够精度。通过有限元模拟和试验结果进行剪力键受力特性的分析和研究有一定的可靠性。

图12 箍筋的竖向位移Fig.12 Vertical displacement of stirrup

图13 箍筋处解剖图Fig.13 Anatomy of the reinforced bar

图14 钢箱的Mises应力Fig.14 Mises stress of steel box
4 剪力键的界面剪切力的发展全过程分析
由于对推出试验现象(尤其是试件内部微观的应力应变的变化过程)的观察存在诸多不便,可利用笔者所述方法建立的有限元模型对剪力连接件中钢-混凝土间的界面剪切力的发展过程进行微观分析,以之补充试验中无法观测的内容。将有限元模型计算得到的荷载-滑移全过程曲线划分为A~K共11个时间步作为分析的对象(见图18)。

图15 A试件计算值与试验值比较Fig.15 Comparison of calculation and test value of specimen A
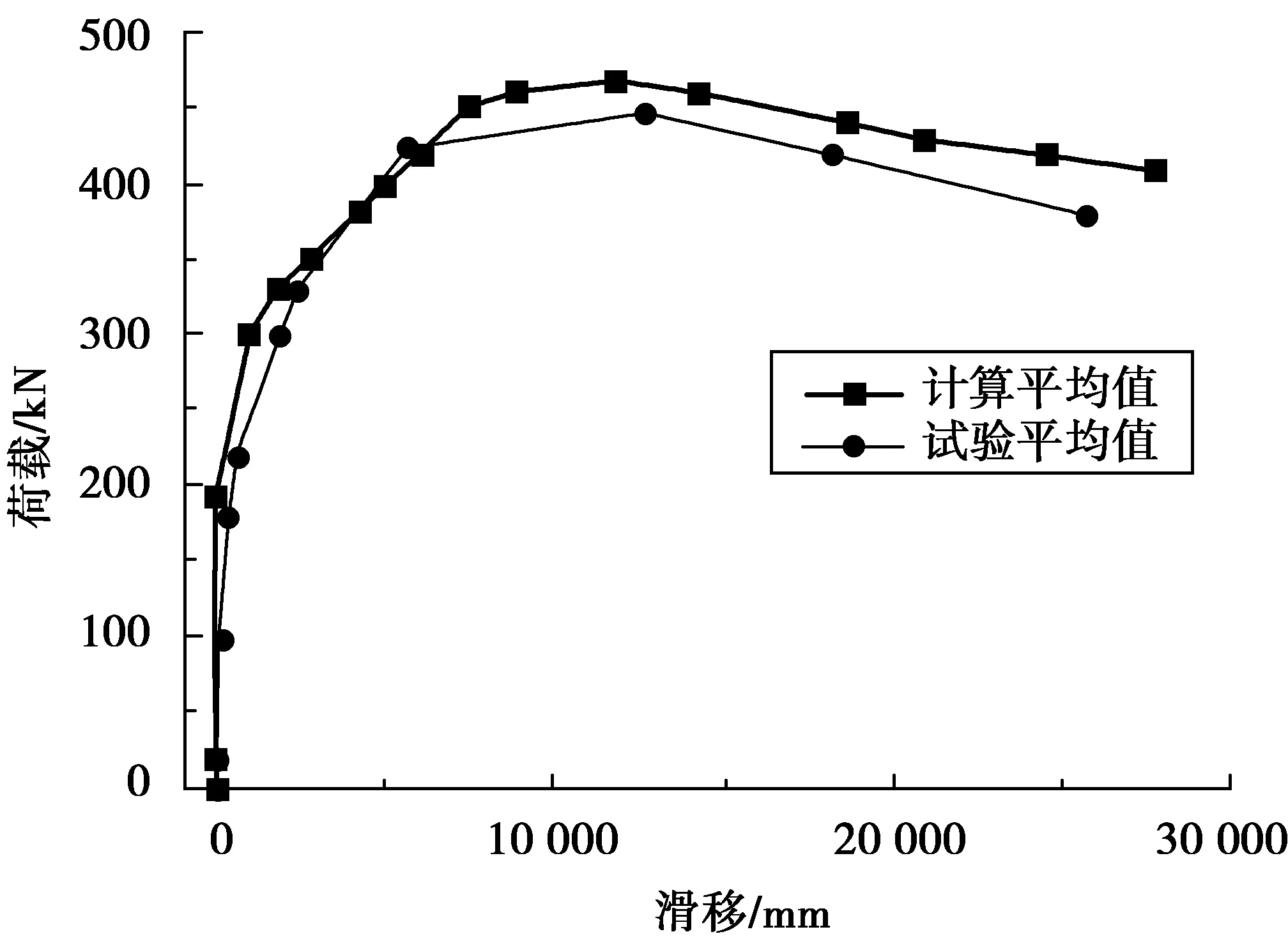
图16 B3试件计算值与试验值比较Fig.16 Comparison of calculation and test value of specimen B3

图17 B5试件计算值与试验值比较Fig.17 Comparison of calculation and test value of specimen B5
结合模型的计算结果(图19~图22)和试验现象分析开孔板与混凝土间界面效应的发展过程如下:
1)在弹性阶段,试件界面单元剪切力在试件底部率先增大,随着前后钢板与混凝土之间出现微小滑动,界面的胶结力发生破坏,钢板表面机械咬合力开始发挥作用,随着荷载的增大,钢板两端附近界面上的相对滑动增大,且发生相对滑动的区域逐渐向界面中间靠拢,最终应力界面上的胶结力和机械咬合力的总值达到最大值,与推出试验中弹性阶段内界面裂缝由试件两侧向中间延伸并达到贯通的模式相同。
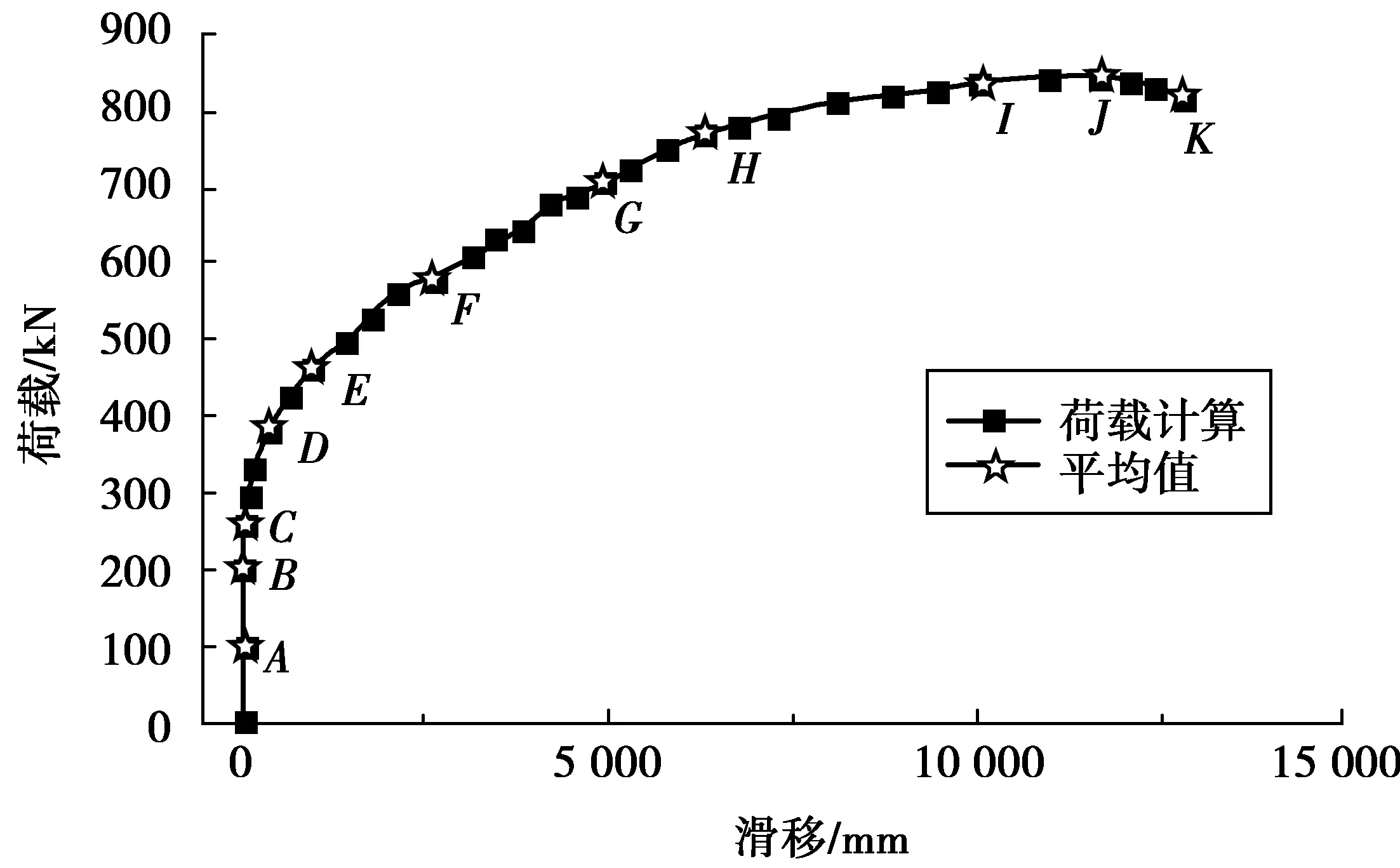
图18 试件模型荷载-滑移曲线Fig.18 Load-slip curve of the test model
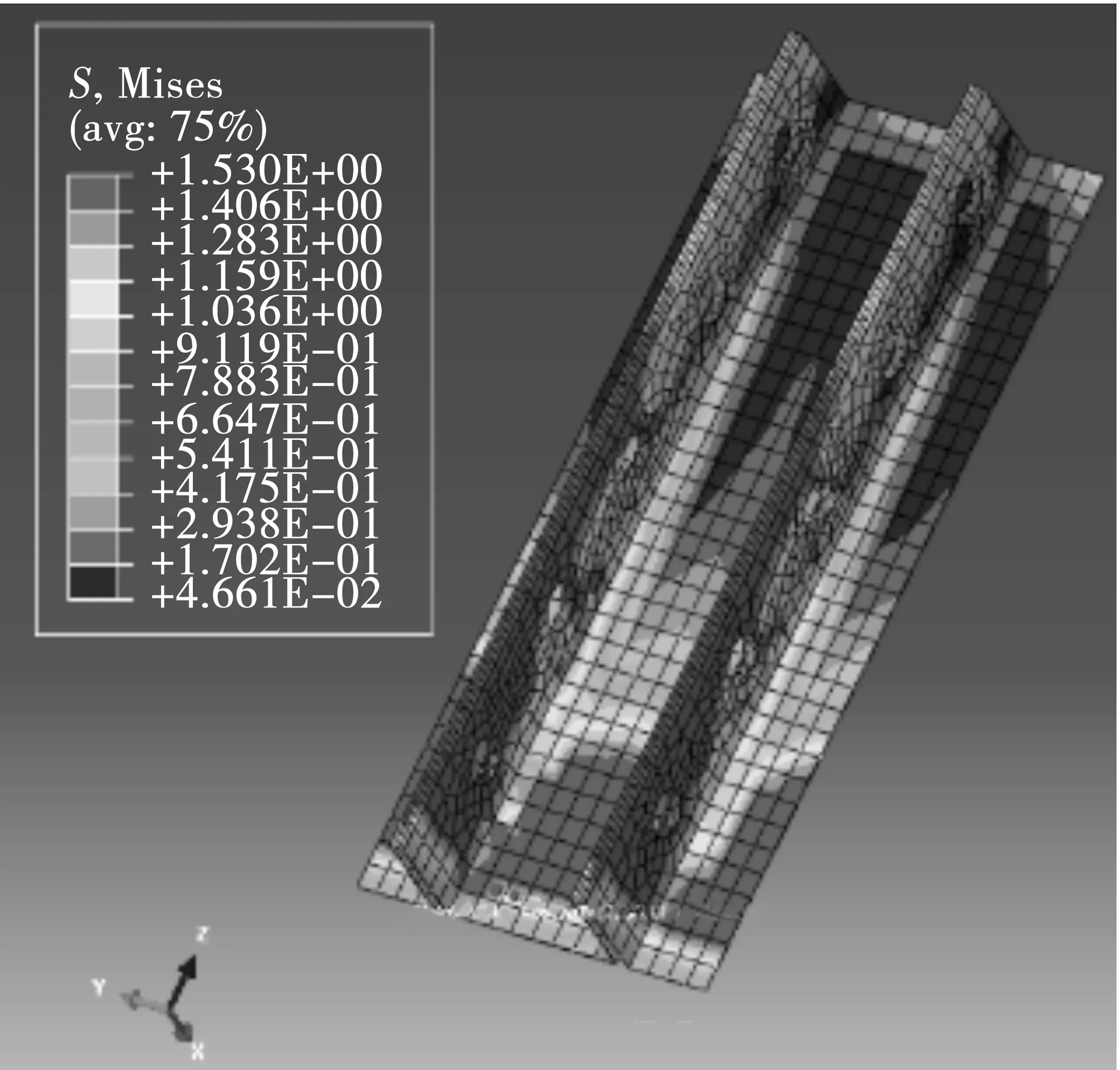
图19 A点处界面应力分布Fig.19 Interface stress distribution of step A
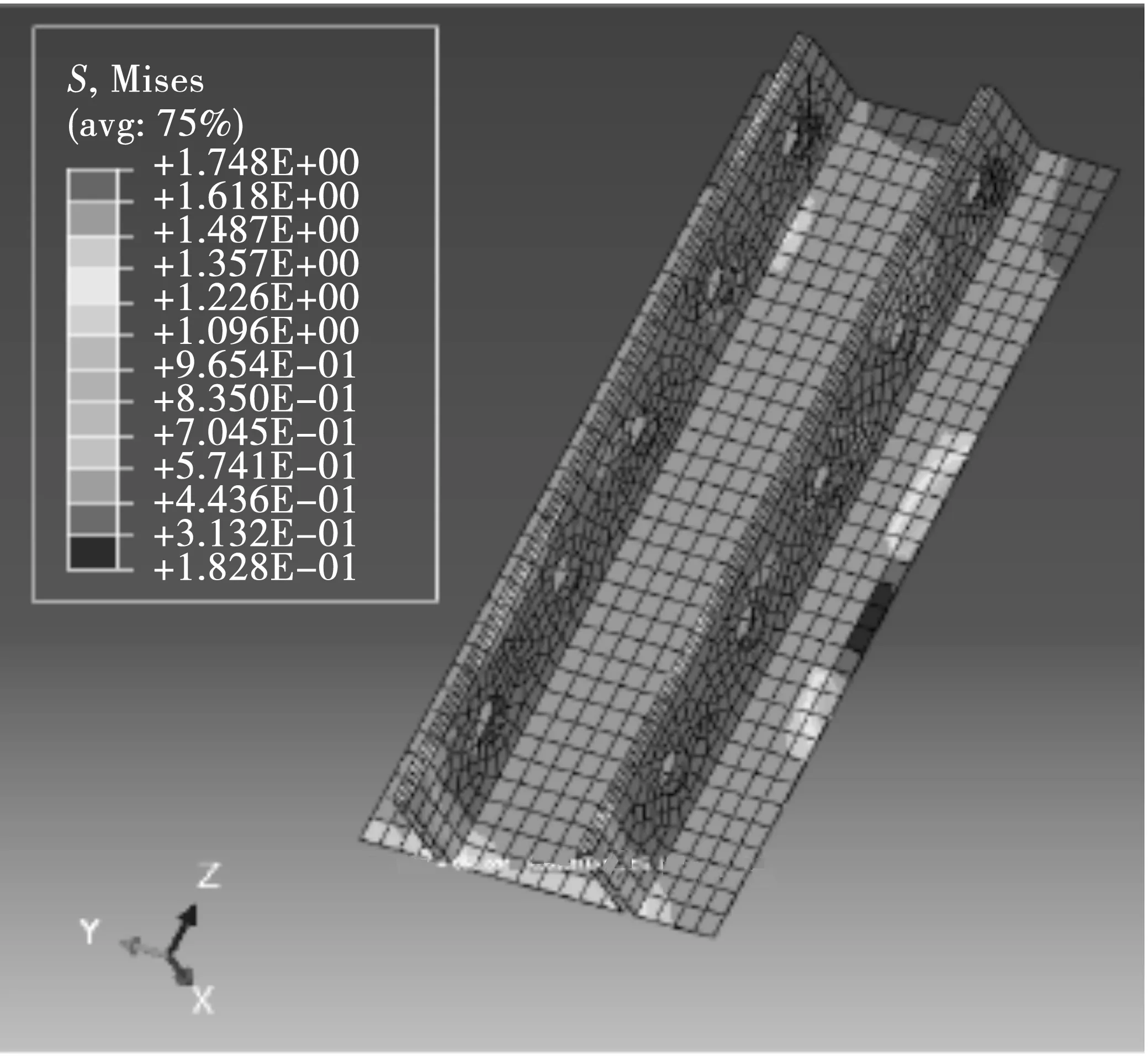
图20 D点处界面应力分布Fig.20 Interface stress distribution of step D
2)在弹塑性阶段初期界面单元的应力在弹性阶段的基础上继续增大直至试件底部界面单元应力达到所设定的应力极限,然后界面底部应力极限区域的范围逐渐扩大向试件顶部延伸。
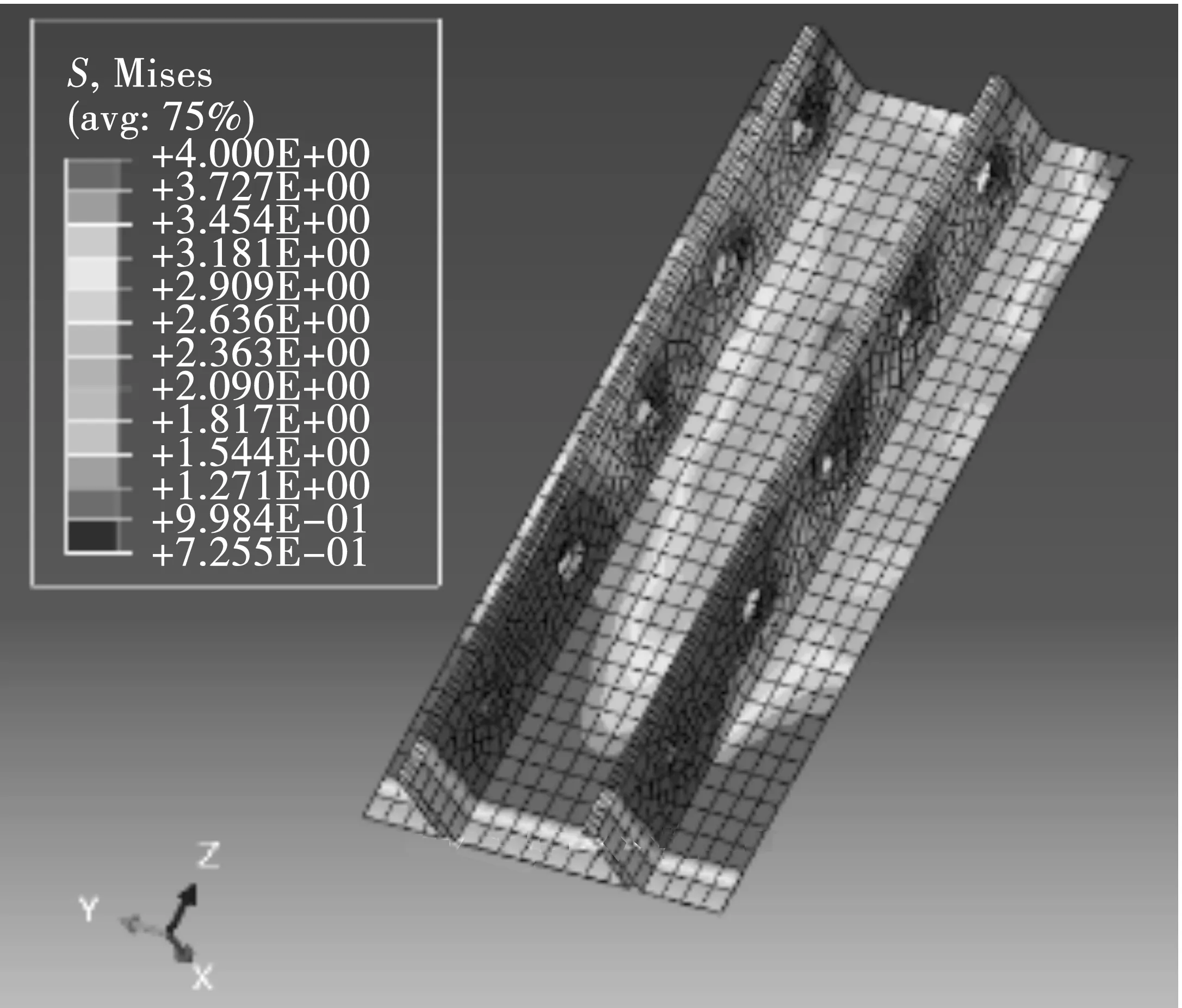
图22 K点处界面应力分布Fig.22 Interface stress distribution of step K
3)当试件进入破坏阶段以后,滑移量快速发展,界面底部混凝土与钢箱间的接触表面被逐渐锉平,机械咬合力迅速衰减,界面剪切力主要由界面摩擦力提供,界面底部应力极限区域的范围不断向顶部扩展。
5 结 论
笔者采用了一种兼顾精确性与实用性的界面单元模拟钢-混凝土界面,成功地建立了组合结构剪力连接件的有限元模型,结论如下:
1)提出了一种采用特定形式超弹性材料虚拟界面单元与束缚约束相结合的钢-混凝土组合结构界面模拟方法。该界面单元材料本构关系可通过推出实验结果确定,并可应用到同类材料的组合结构界面的有限元模拟中。
2)笔者建议采用塑性损伤模型模拟钢-混凝土组合结构中的混凝土,可以较好地避免由于钢-混凝土结合界面出混凝土局部应力集中时易出现的计算难以收敛现象,并模拟出混凝土进入下降段后的性状。文中模拟案例表明混凝土的表现与试验破坏现象较吻合。
3)通过对某组合结构剪力键推出试验的模拟表明,采用本方法模拟钢-混凝土界面得到的剪力连接件理论模型的计算破坏现象与实际破坏现象、计算荷载滑移曲线与试验值吻合良好。计算模型的求解过程可以完整反映剪力连接件在整个加载过程中的承载情况,基于ABAQUS有限元模型仿真分析研究连接件的受力情况是可靠的。
4)基于试验现象和模型的计算结果得到剪力键的钢-混凝土界面效应的发展过程:弹性阶段界面上出现微小滑动,界面抗剪主要由胶结力和机械咬合力提供;弹塑性阶段所有界面上的机械咬合力陆续破坏,抗剪主要由摩擦力和残余的机械咬合力提供;弹塑性阶段后期和破坏阶段界面表面逐渐被锉平,界面剪切力主要由界面摩擦力提供,界面底部应力首先达到极限应力并且极限应力区域不断向试件顶部扩展。
[1] 肖林. 钢-混组合结构中PBL剪力键的静力及疲劳性能研究[D].成都:西南交通大学,2012:1-2. XIAO Lin.StudyofStaticandFatigueBehaviorofPBLShearConnectors[D].Chengdu: Southwest Jiaotong University, 2012: 1-2.
[2] 曹学亮,李法雄.基于ABAQUS的开孔板连接件抗剪承载力分析[J].公路交通科技, 2013,30(11): 89-95. CHAO Xueliang,LI Faxiong.Analysis of shear-capacity of perfobond shear connectors based on ABAQUS software[J].JournalofHighwayandTransportationResearchandDevelopment,2013,30(11):89-95.
[3] 黄远,聂建国,易违建.考虑滑移效应的钢-混凝土组合框架梁的刚度研究[J].工程力学,2012,29(11): 88-92. HUANG Yuan, NIE Jianguo, YI Weijian. Stiffness of steel-concrete composite frame beam with slip effect[J].EngineeringMechanics, 2012, 29(11): 88-92.
[4] 方秦,还毅,张亚栋.ABAQUS混凝土损伤塑性模型的静力性能分析[J].解放军理工大学学报,2007,8(3):254-260. FANG Qin, HUAN Yi, ZHANG Yadong. Investigation into static properties of damaged plasticity model for concrete in ABAQUS [J].JournalofPLAUniversityofScienceandTechnology, 2007, 8(3): 254-260.
[5] 李杰,陈建兵,吴建营.混凝土随机损伤力学[M].上海:科学出版社, 2014:25-30. LI Jie, CHEN Jianbing, WU Jianying.StochasticDamageMechanicsofConcreteStructures[M].Shanghai: Science Press, 2014: 25-30.
[6] ABAQUS, Inc.ABAQUSAnalysisUser’sManaualv6.10[M]. Washington: ABAQUS Inc, 2010:1025-1036.
[7] 范亮.钢箱-混凝土组合拱截面受力行为与设计原理研究[D].成都:西南交通大学,2010:70-72. FAN Liang.StudyontheMechanicalBehaviorsandDesignPrinciplesofSteelBox-ConcreteCompositeArchSections[D].Chengdu: Southwest Jiaotong University, 2010: 70-72.
[8] 白光亮.大跨度斜拉桥索塔锚固区结构行为与模型试验研究[D]:成都:西南交通大学,2009:34-35. BAI Guangliang.StudyontheStructuralBehaviorsandExperimentsofAnchorageZoneofCable-StayedBridge[D].Chengdu: Southwest Jiaotong University, 2009: 34-35.
[9] 吴立彬. 基于三线性黏结-滑移本构模型的FRP-混凝土界面行为研究[D]:广州:暨南大学,2010:9-12. WU Libin.StudiesonFRP-ConcreteInterfacewithTri-linerBond-SlipLaw[D].Guangzhou: Ji′nan University, 2010: 9-12.
[10] 林建平.考虑界面非连续变形的钢-混凝土组合梁桥数值模拟研究[D]杭州:浙江大学,2014:7-12. LIN Jinping. Study on numerical simulation of steel-concrete composite bridge considering interface discontinuous deformation [D]. Hangzhou: Zhejiang University, 2014: 7-12.
[11] 范亮,何骏.埋入式钢板-混凝土界面抗剪性能试验研究[J].重庆交通大学学报(自然科学版),2015,34(3):23-27. FAN Liang, HE Jun. Experimental study on shear performance of embedded steel plate and concrete interface[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2015, 34(3): 23-27.
[12] 庄茁.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009:251-252. ZHUANG Zhuo.AnalysisandApplicationofFiniteElementsBasedonABAQUS[M].Beijing: Tsinghua University Press, 2009: 251-252.
[13] JGSD S, LROD L, PCGDS V, et al. Nonlinear dynamic analysis of steel portal frames with semi-rigid connections[J].EngineeringStructures,2008, 30(9): 2566-2579.
[14] 何骏.钢箱-混凝土结构多排PBH剪力键传力机制试验研究[D].重庆:重庆交通大学,2015:10-15. HE Jun.ExperimentalResearchonMechanicalBehaviorsofMultiple-rowPBHShearConnectorsinSteelBoxConcreteCompositeMembers[D]. Chongqing: Chongqing Jiaotong University, 2015: 10-15.
[15] 秦浩,赵宪忠.ABAQUS混凝土损伤因子取值方法研究[J].结构工程师,2013,29(6):27-32. QIN Hao, ZHAO Xianzhong. Study on the ABAQUS damage parameter in the concrete damage plasticity model[J].StructureEngineers, 2013, 29(6):27-32.
(责任编辑:朱汉容)
Finite Element Simulation Method of Steel-Concrete Composite Structure Considering the Interface Effect
FAN Liang1, LI Xiao1, HE Jun2
(1. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P. R. China;2. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310006, Zhejiang, P. R. China)
Due to the complexity of a shear transfer problem of the contract interface between steel and concrete, there are various finite element simulation methods on the steel-concrete composite structure currently. However, most of the methods are either too complicated for technical problems or too experiential which depends on many test results to determine the parameters. Therefore, considering the idea of combination of practicality and accuracy, a method using specific hyper elastic virtual interface element was proposed to simulate the steel-concrete composite structure. And it also suggested the concrete plastic damage model can be adopted. The proposed method was applied to the numerical simulation of the mechanical property and interfacial shear force in the whole development process of composite structure shear connector’s push-out tests. The results show that the proposed method is feasible and reliable, which is applicable to the FE simulation of the steel-concrete composite structure considering the interfacial bond slip effect.
bridge engineering; steel-concrete composite structure; finite element simulation; bond slip; push out test
10.3969/j.issn.1674-0696.2017.07.02
2016- 02-25;
2016- 04- 06
国家自然科学基金项目(51308571)
范 亮(1979—),女,安徽芜湖人,副教授,博士,主要从事钢筋混凝土组合结构研究。E-mail:fanliangcq@mail.com。
TU 398.9
A
1674-0696(2017)07- 007-08

