基于混沌系统的SM4密钥扩展算法∗

王传福 丁群

(黑龙江大学电子工程学院,哈尔滨 150080)

基于混沌系统的SM4密钥扩展算法∗

王传福 丁群†

(黑龙江大学电子工程学院,哈尔滨 150080)

(2016年8月21日收到;2016年11月6日收到修改稿)

分组密码是一类广泛使用的加密方法.在网络数据加密体系中,为提高信息的安全性,需要保证初始密钥具有足够大的密钥空间.为克服量子计算机对短密钥的威胁,一种基于混沌映射的新型密钥扩展算法被提出.该算法将混沌映射融入到原SM4密钥扩展算法中,有效增大了密钥空间,提高了破译难度.

混沌,密钥扩展算法,现场可编程门阵列

1 引 言

信息时代的到来,大数据的分析和处理是现在许多科技领域的基础.随着网络通信技术的进步,网络中数据传输的安全性越来越受到重视.美国首先推出了DES数据加密标准算法,由于密钥空间较小不久就被成功破译.随后在2002年,著名的高级加密标准AES正式发布.至今,AES已经成为运用最为广泛的分组加密算法.在我国众多学者的不断努力下,研发出了WAPI无线网络标准加密算法SMS4算法[1],于2012年被国家商用密码管理局确定为国家密码行业标准,并更名为SM4算法.SM4算法是基于Feistel结构的32轮迭代运算,具有加、解密的自相似性,被广泛运用在互联网数据的安全传输中.

混沌是近几十年来兴起的一门新型学科[2-5],固有的复杂动力学特性使得其具有初始值敏感性、内在随机性、运动轨道遍历性和确定性等诸多特性.这些特性与Shannon提出的“混淆性”和“扩散性”相一致,为将混沌系统运用于密码学提供了理论基础.混沌与密码学的结合设计与应用俨然成为密码学中的一个新方向.近几年来,许多学者致力于混沌和密码学的研究并得到了显著的成果.将混沌运用于分组密码体系中的混合密码有着广泛的运用前景,特别是将混沌特性融入原有的密钥扩展算法中.2005年权安静等[6]将超混沌映射引入DES和AES算法中.初始密钥作为超混沌映射输入,生成的伪随机序列为DES,AES密钥扩展算法的输出.2008年赵芮等[7]提出二维Logistic与Chebyshev映射来代替整个密钥扩展算法,并提出了一次一密思想,扩大了原算法的密钥空间.赵芮等仅详细讨论了加密算法.由于密钥实时在变化,该思想下的解密算法不能得到正确的解密.2009年陈红和陈谊[8]提出利用Logistic混沌系统直接替换AES的密钥扩展算法.该算法增强了AES轮密钥间的随机性.对于混沌系统与分组密码结合的架构大致如此.有的学者也提出其他混合算法,但在架构上无太大改变,仅在混沌系统选取上有所变化.

2006年胡祥义和刘彤[9]提出了动态对称密码的思想.2008年,蒋继娅等[10]给出了实现方案.该方案需要利用大量的存储单元对伪随机数存储,通过每次加密时选取不同的伪随机序列值进行动态加密.2011年,周术洋等[11]结合了动态对称密码的思想提出了动态的SM4加密算法.并在蒋继娅、刘彤、胡祥义等基础上减少了存储单元.同年,赵尔凡、赵耿将混沌系统和SM4算法相结合,提出了基于Logistic和Tent映射下的SM4算法.该算法不仅利用Logistic和Tent映射代替原密钥扩展算法,而且还生成了动态S盒.基于以上专家、学者们对分组密码融合混沌的研究,本文提出一种基于混沌映射的密钥扩展算法.该密钥扩展算法在保留原分组密码的密钥扩展算法上,增加了低精度混沌映射.该算法与现存的混沌密钥扩展算法相比,不仅增大了密钥空间,增强了轮密钥间的随机性,更使加密后的密文仅与密钥、明文相关,与任何静态存储值无关.

2 混沌系统的选取与设计

本文采用混沌系统对原密钥扩展算法进行融合,极大地增加了原轮密钥间的随机性.由于硬件实现上受逻辑资源的限制,故该混沌系统选用Logistic映射,其表达式如下：

其中n∈(0,1,2,3,···),xn∈(0,1).µ为系统参数,µ∈(0,4].x0为混沌初始值.xn为本次迭代值,xn+1为本次迭代输出值.虽然Logistic混沌映射具有混沌系统的诸多优质特性,但将其融入到特定背景下的密码学算法中仍有许多问题值得注意.

2.1 混沌参数及初始值选取

Logistic映射中的µ作为系统参数,µ的取值控制着系统是否具有混沌特性.当µ∈(3.5699456,4]时Logistic映射处于混沌区.Logistic映射分叉图如图1所示.

图1 Logistic映射分叉图Fig.1.Bifurcation diagram of Logistic map.

陈红和陈谊[8]以及潘晶等[12]选用µ和x0作为初始密钥,在增强轮密钥随机性的同时也增大了密钥空间.但由图1所示,在µ∈(3.5699456,4]时,有周期窗口出现.该现象说明Logistic映射处在混沌区时,仍会出现周期性.该周期窗口主要出现在µ∈(3.828,3.875].µ值参数选取对Logistic轨道的影响如表1所列[13].

表1µ值参数选取Table 1.The selection ofµvalue.

仅在µ∈(3.571448,3.82842]与µ∈(3.9,4]时存在混沌轨迹.将参数µ作为初始密钥的输入,仅使初始密钥的密钥空间略有增加.由于参数µ取值范围过窄,密钥交换后的初始密钥需要通过选取特定区间的值作为真正的加密初始密钥,对整个加密算法带来不便.因此,参数µ尽量不作为初始密钥使用.如图1所示,当µ=4时Logistic混沌具有明显的轨道全遍历性.4为2的倍数,便于Logistic映射数字化的实现.因此,参数µ选取固定值4,仅混沌初始值x0作为初始密钥.

2.2 混沌数字化

以上讨论皆是Logistic混沌映射在实数领域中的特性.由于网络数据传输都是离散二值序列.因此,将Logistic混沌映射运用于实际数字电路中时,需要进行数字化处理.混沌序列处理方法有许多种,如二值量化、位序列设计、区间量化、整数求余量化等[14].其中位序列设计具有操作简单、节省资源消耗、一次能出多个二值序列等优点.该方法有利于硬件并行运算,提高算法实现的速度.位序列设计的主要思想是将混沌实值序列用有限长度的浮点数表示,取出全部或从中抽取几位二值序列作为二值量化后的结果.计算机中的数据本来就是以浮点数形式表示,在硬件实现中可转化为定点数表示,相比浮点数提高了几位有效精度.因为xn的取值范围为小数,十进制与二进制之间转化公式为

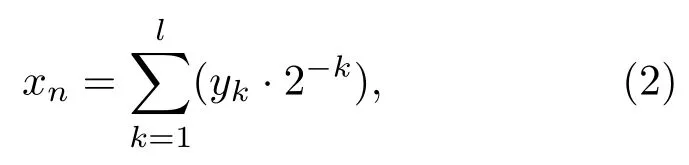
其中yk∈{0,1},k为小数点后第k位.因此,可将十进制小数转化为二进制小数：

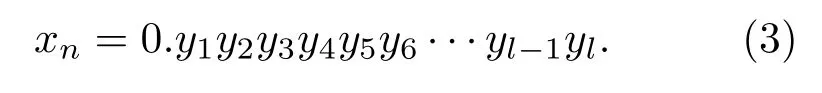
由于FPGA不能直接计算小数,故将二进制小数转化为定点整数,对(2)式两边同乘2l进行定点化：

那么,定点化后的二进制小数为

定点化后的二进制序列可由yk直接表示.利用混沌映射迭代一次可得二进制随机序列l位,实现速度最多是二值量化、区间量化的l倍.

2.3 混沌序列随机性检测

美国国家标准与技术研究院(NIST)推出NIST测试程序包,用来测试随机数.有频率检测、块内频数检测和游程检测等多种测试手段.该测试主要检测量化后任意长度的二进制序列,主要致力于判断可能存在于序列中各种各样的非随机性.对Logistic混沌序列测试结果可知,24位、32位等低精度的Logistic测试并未达到标准.该检测表明Logistic映射输出具有周期性.混沌映射经过数字化后受到有限字长效应,混沌特性逐渐退化,输出序列产生周期性[15-17].量化后的混沌映射随着量化位数精度的增加,输出序列凸显的周期性逐渐减弱.因此,低量化位数精度的Logistic映射输出值不能成为随机性较完美的二值序列.NIST序列测试是检测大量二值序列的随机性,主要运用在流密码的检测.本文中Logistic映射并不作为流密码使用,而是仅取输出序列中的部分序列来去除原SM4密钥扩展算法中轮密钥间的相关性.由于SM4密钥扩展算法仅需要32个32比特的随机序列,因此只需要在Logistic映射输出序列中选取32个32比特短序列即可.该部分序列能够保证具有良好的随机性.混沌映射或混沌方程往往包含乘法或除法.随着乘法位数的增加,硬件资源的消耗急剧增大.分组密码较流密码而言,其硬件实现资源消耗相对较多.此时利用高精度的混沌映射来替代原分组密码的密钥扩展算法,硬件实现资源消耗较多.仅利用部分序列的随机特性参与密钥扩展运算的算法极大地减少了Logistic映射硬件实现的工作量,并同时增加了轮密钥间的随机性.

2.4 Logistic混沌映射的实现

由(1)式可知,Logistic混沌映射基于循环迭代结构.Logistic混沌映射原理框图如图2所示.

图2 Logistic原理图Fig.2.The schematic diagram of Logistic.

图2可知,定点化后的Logistic映射公式中(1-xn)模块可通过取反模块与+1模块快速实现.利用FPGA(现场可编程门阵列)硬件实现的物理RTL(寄存器转换级电路)图如图3所示.

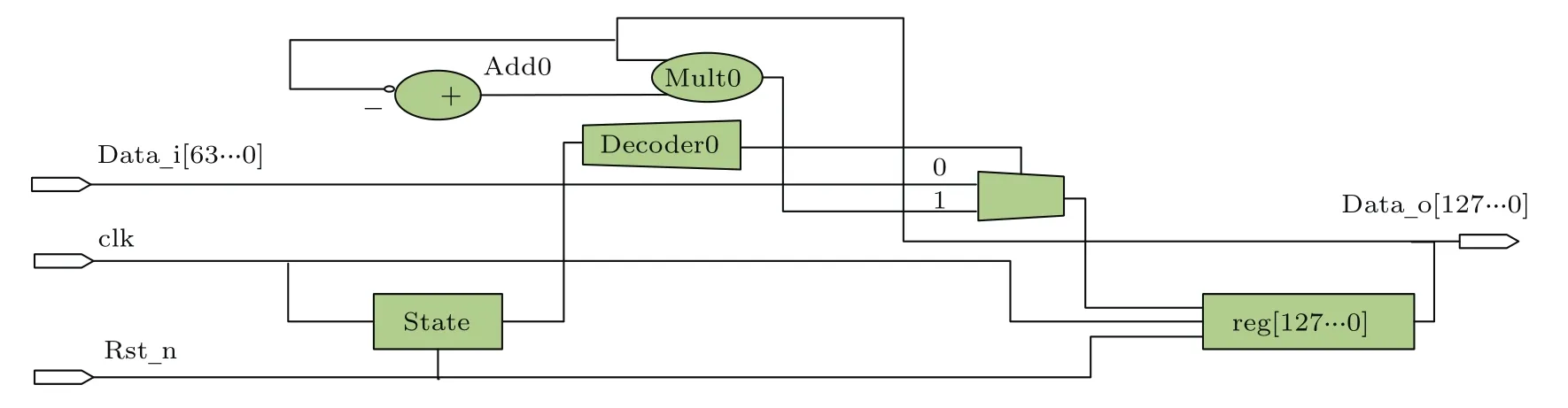
图3 Logistic映射RTL图Fig.3.Logistic mapping RTL schematic.

3 基于混沌SM4 混合加密算法设计

加密算法是保证数据安全传输的理论依据,我国首次推出的互联网数据加密标准商用分组密码是SM4算法.该算法能够有效抵御差分攻击和线性攻击.但相对AES和Camellia算法而言,仍具有密钥空间较小的安全隐患.虽然128位密钥长度支撑的密钥空间在现有的穷举手段下无法破译.但随着量子计算机研究推进,在未来几十年中存在被破译的隐藏危险.

3.1 增加密钥空间思想的提出

本文将SM4密钥扩展算法与混沌系统相结合,提出一种长密钥的动态SM4加密算法,在增加密钥空间的同时也增强了加密系统的破译难度.原SM4密钥扩展算法通过32轮Feistel结构迭代产生,每轮迭代输出一个32比特数Ki+4.每轮迭代框图如图4所示.

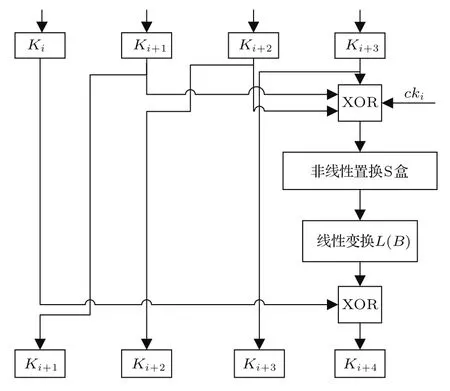
图4 SM4密钥扩展算法Fig.4.SM4 key scheme.

首先将输入的128位初始密钥分为四组,每组32位,由如下符号表示：

整个密钥扩展算法如下.

定义⊕为异或运算.图中XOR为异或操作缩写.首先,

然后对i=0,1,2,3,···,31,有

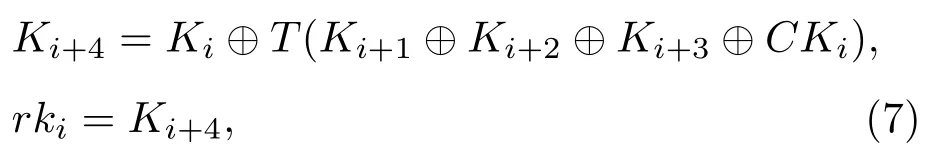
其中函数T包含非线性置换S盒、线性变换L(B)和异或操作.S盒包含256个存储值,作为置换的数据.线性变换函数L(B)为

其中≪为循环左移.该密钥扩展算法中共有36个固定量(十六进制表示)：

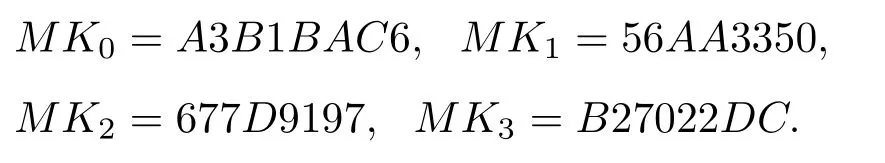
ck0至ck31依次为：

32个固定参数cki由固定的取模算法产生,具有一定的随机特性.原SM4密钥扩展算法通过将cki与Ki+3异或来增加轮密钥间的随机性,并使轮密钥能更好地扩散在每轮的加密算法中.由于32个cki皆为固定数值,带来了密码破译的隐患.因此,本文提出利用混沌映射动态地产生cki值,使SM4算法中不存在固定参数.任何参数都随着初始密钥的改变而改变.因为算法内部参数仅由密钥生成,故整个加密算法输出的密文仅与密钥、明文相关,并无任何固定参数参与密钥扩展算法的运算.

3.2 混沌SM4密钥扩展算法的设计

将原有的固定cki值用每轮混沌映射输出值代替.基于混沌的SM4密钥扩展算法如图5所示.利用quartusII软件对改进后的加密算法进行仿真可得硬件电路图如图6所示.Modelsim仿真工具输出的32个cki值如图7所示.

图5 基于混沌的SM4密钥扩展算法Fig.5.SM4 key scheme based on chaos.

图6 (网刊彩色)基于混沌的SM4密钥扩展算法电路图Fig.6.(color online)SM4 key scheme circuit based on chaos.

图7 基于混沌的SM4密钥扩展仿真图Fig.7.SM4 key scheme simulation based on chaos.

4 资源分析

表2显示了本文算法在不同位数精度下的资源消耗.位数为混沌系统的数字化精度;LUT为FPGA内基本逻辑单元;Multiple 9-bit为FPGA片上集成的9比特乘法器;Key space为密钥空间大小.由表2可知128位精度下,混沌系统LUT消耗913个,保留的原SM4密钥扩展算法LUT消耗1324个,Multiple 9-bit消耗72个,密钥空间为256位.

作者对一维Logistic代替SM4密钥扩展[8]、多维或多个混沌系统代替SM4密钥扩展[6,7]、预存储的SM4密钥扩展[9-11]这三种算法进行了FPGA设计与仿真,其中多维或多个混沌系统取Lorenz混沌系统为代表,预存储法取128个32位的预存储为基础.通过参考、借鉴相关的方法和思路[18,19],将这三种算法所得资源消耗数据情况、密钥空间大小与本文算法相互比较,可得四种算法资源消耗与密钥空间对比图,如图8所示.

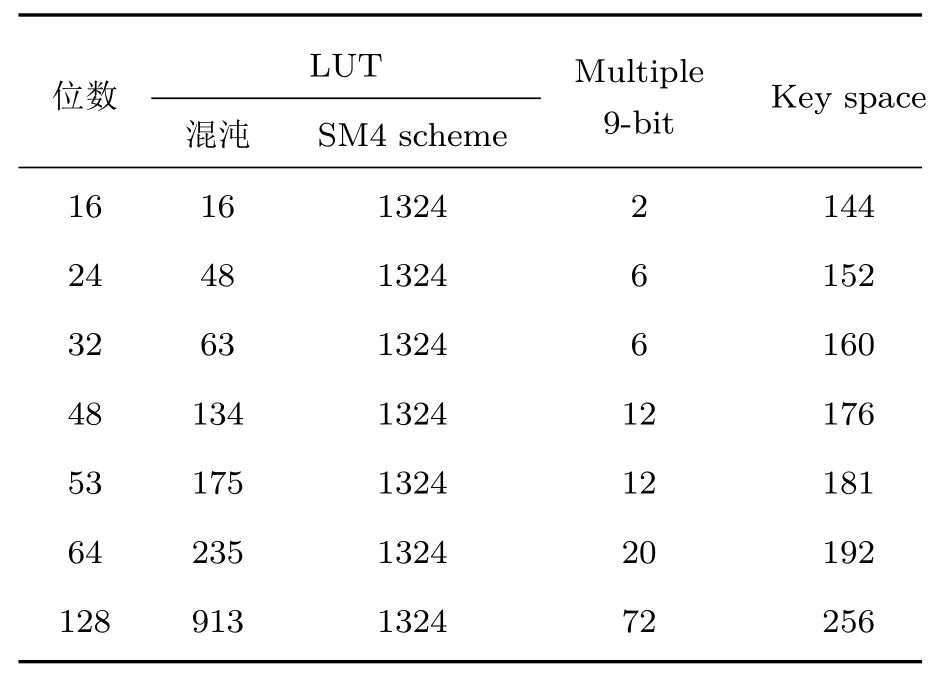
表2 资源消耗和密钥空间Table 2.Resource consumption and key space.

如图8(a)所示,在LUT资源消耗上,本文算法在不同的位数精度上都比一维Logistic混沌系统替代算法多1324个LUT消耗.因为该消耗是为了保留原SM4密钥扩展算法而产生的.一维Logistic混沌系统替代算法虽然LUT资源消耗最少,但是密钥空间小,不利于加密;多维或多个混沌系统替换算法在64位数精度以后的资源消耗急速增加;预存储方法稳定在5420个LUT.

如图8(b)所示,本文算法消耗的Multiple 9-bit数与一维Logistic混沌系统替代算法相同;本文算法与多维或多个混沌系统替换算法相比,Multiple 9-bit数明显较少;预存储的SM4密钥扩展算法则无Multiple 9-bit数的消耗,但其密钥空间小不利于加密.

由图8(c)知,Lorenz密钥空间随位数增加的速度增长最快.因为Lorenz属于三维混沌系统,由X,Y,Z三个变量构成.当X,Y,Z位数精度达到128位时,初始密钥可由X,Y,Z三个初始值构成,为384位.但此时LUT,Multiple 9-bit资源消耗巨大,密钥扩展算法与整个SM4加密算法所用资源相当,等于占有了2个SM4资源.如果256位密钥空间足以抵抗量子计算机的穷举破解,利用巨大的资源去换取足以保证数据安全情况下更多额外的密钥空间值得商榷.

预存储算法下LUT资源消耗与预存的cki个数有关.该算法的资源消耗取决于提前预存的cki的个数.若存储128个cki值,则需4096个存储单元,且该算法并未增加密钥空间.为使预存储算法具有更好的随机性,将原32个固定参数cki扩充为近千个并用寄存器提前预存[9-11].当加密时,从中任意选取32个作为本次固定参数cki的值.该算法加密时,选取cki后若用该固定值持续加密,则与原SM4密钥扩展算法在本质上并无差别.如果每次加密时重新选取32个cki值,则会因为重新计算轮密钥而产生多个延迟周期,降低了加密吞吐量,并在解密时需要产生额外同步信息.本文加密算法无任何固定值的存储,所有信息全由密钥产生.密钥为双方所共知,与预存储方法相比本文方法以密钥为同步信息,在密钥空间加大的前提下使得算法动态特性大大提升.

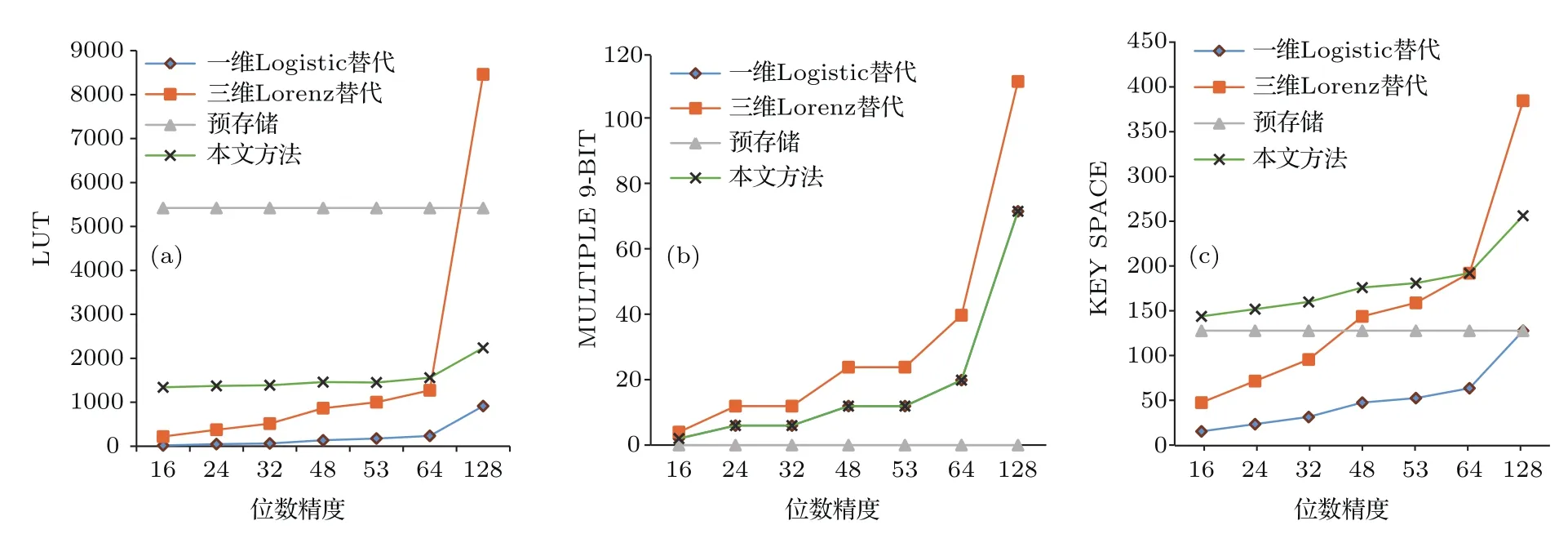
图8 四种算法资源消耗与密钥空间对比 (a)逻辑资源使用个数;(b)9比特乘法器使用个数;(c)密钥空间Fig.8.The contrast of four kinds of resources consumption and the key space：(a)LUT resource consumption;(b)multiple 9-bit resource consumption;(c)key space.

5 安全性分析

密钥扩展算法是迭代分组密码的重要组成部分,对于绝大多数的迭代分组密码,都由种子密钥生成轮密钥的算法,该算法被称为密钥扩展算法.密钥扩展算法的设计目的是使轮密钥具有统计独立和灵敏性.轮密钥间的统计独立是难以实现的,只是尽可能地使轮密钥趋近于统计独立.轮密钥的灵敏性是指初始密钥细微的改变就能使输出的轮密钥产生巨大的改变.对此,混沌系统的初始值敏感性、内在随机性、运动轨道遍历性等诸多特性恰好能够满足密钥扩展算法设计的需求.

现在对密钥扩展算法的攻击具有旁路攻击[20]、信道攻击等相关攻击方法.为了抵抗相关密钥扩展算法的攻击,非线性早已被引入到现有密钥扩展算法中.这种非线性的强弱对阻止仅由密码密钥的差分来完全确定密钥扩展的差分具有较大的影响.其中旁路攻击主要是利用密码算法实现过程中的中间状态信息进行攻击.通过基于密钥编排故障的SM4密钥扩展算法的差分故障攻击能够快速有效地恢复出参与每轮加密的轮密钥.在原SM4密钥扩展算法进行到第32轮时,通过对存储单元K31,K32,K33和K34进行故障诱导,随机改变其中任意值产生第32轮错误的轮密钥.将该错误轮密钥参与第32轮SM4加密算法的运算,并得到错误的加密数据.通过SM4加密算法中第32轮的明文与正确密文对、明文与错误密文对进行差分攻击,恢复出该轮加密时使用的正确轮密钥.受到故障诱导后的轮密钥K31,K32,K33和K34需要通过异或、非线性置换S盒、线性变换L(B)才能得到下一轮错误的轮密钥.在第一步异或过程中需要与额外的固定参数ck32异或.在原SM4密钥扩展算法中cki是固定参数.虽然cki间具有一定的随机性,但其为固定值,在轮密钥逆推过程中存在隐藏的安全隐患.本文算法cki全由初始密钥动态生成,随着初始密钥的改变而改变,不为攻击者所知.cki全由Logistic混沌系统产生,而混沌的内在随机性能很好地抵抗差分攻击[21],从而增加了密钥扩展算法的安全性.对数据进行安全性分析具有多种方法[22,23],本文通过参考这些理论方法,将原SM4密钥扩展算法输出的轮密钥与本文方法产生的轮密钥进行NIST随机数测试.本文产生的部分测试数据如表3所列.

表3 轮密钥的NIST测试Table 3.The NIST test of subkey.

如表3所列,由本文方法产生的轮密钥与原SM4密钥扩展算法相比,轮密钥间的随机性有明显增强.

6 结 论

本文提出了一种基于混沌的SM4密钥扩展算法,该算法有效地增大了SM4密钥空间,增强了SM4算法破译难度.与一般基于混沌的密钥扩展算法相比着重考虑了硬件的资源消耗情况和算法的动态特性,在增大密钥空间的同时,也增强了算法破译的难度.混沌映射输出具有良好的随机特性,基于混沌的密钥扩展算法加强了轮密钥间的随机性.新型密钥扩展算法将原来固定参数与初始密钥相关联,将原静态存储的固定参数变为动态生成.整个SM4加密算法中不再存在任何固定的随机参数.每个参数都与初始密钥息息相关,加强了SM4算法的动态特性.本算法利用FPGA进行了硬件实现.经实验证明,该算法具有可行性.

[1]Shen C X,Zhamg H G,Feng D G,Chao Z F,Huang J W 2007Sci.China Ser.E37 129(in Chinese)[沈昌祥,张焕国,冯登国,曹珍富,黄继武2007中国科学37 129]

[2]Wu G C,Baleanu D 2014Signal Process.102 96

[3]Wang E F,Wang Z,Jing M A,Ding Q 2011J.Net.6 1025

[4]Liu H,Kadir A 2015Signal Process.113 104

[5]Tang S,Chen H F,Hwang S K,Liu J M 2002IEEE T.Circuits-I.49 163

[6]Quan A J,Jiang G P,Zuo T,Chen T 2005J.Nanjing University of Posts and Telecommunications25 80(in Chinese)[权安静,蒋国平,左涛,陈婷2005南京邮电大学学报25 80]

[7]Zhao R,Wang Q S,Wen H P 2008Microcomputer Information24 43(in Chinese)[赵芮,王庆生,温会平2008微计算机信息24 43]

[8]Chen H,Chen Y 2009J.Food Science and Technology27 57(in Chinese)[陈红,陈谊 2009食品科学技术学报27 57]

[9]Hu X Y,Liu T 2006Network Security Technology&Application3 69(in Chinese)[胡祥义,刘彤 2006网络安全技术与应用3 69]

[10]Jiang J Y,Liu T,Hu X Y 2008Network Security Technology&Application9 92(in Chinese)[蒋继娅,刘彤,胡祥义2008网络安全技术与应用9 92]

[11]Zhou S Y,P M M,Xiao X H 2011Microelectronics&Computer28 86(in Chinese)[周术洋,彭蔓蔓,肖小欢2011微电子学与计算机28 86]

[12]Pan J,Qi N,Xue B B,Ding Q 2012Acta Phys.Sin.61 180504(in Chinese)[潘晶,齐娜,薛兵兵,丁群 2012物理学报61 180504]

[13]Zhao G,Zheng D L,Dong J Y 2001J.University of Science and Technology Beijing23 173(in Chinese)[赵耿,郑德玲,董冀媛2001北京科技大学学报23 173]

[14]Dong B H,Zhou J Y,Huang J Y 2009Information Security and Communications Privacy8 327(in Chinese)[董斌辉,周健勇,黄金源2009信息安全与通信保密8 327]

[15]Cermak J,Kisela T,Nechvatal L 2013Appl.Math.Comput.219 7012

[16]Ding Q,Wang L 2011Chinese J.Scientific Instrument 32231 6(in Chinese)[丁群,王路 2011仪器仪表学报231 6]

[17]Yu N,Ding Q,Chen H 2007J.Communs.28 73(in Chinese)[于娜,丁群,陈红2007通信学报28 73]

[18]Zhang Y H,Sun X M,Wang B W 2016China Commun.13 16

[19]Gu B,Sheng V S 2016IEEE T.Neur.Net.Lear.1 1

[20]Li W,Wu D G 2008J.Communs.29 135(in Chinese)[李玮,谷大武 2008通信学报29 135]

[21]Sheng L Y,Wen J,Cao L L,Xiao Y Y 2007Acta Phys.Sin.56 78(in Chinese)[盛利元,闻姜,曹莉凌,肖燕予2007物理学报56 78]

[22]Fu Z,Ren K,Shu J,Sun X 2016IEEE T.Parall.Distr.27 2546

[23]Fu Z J,Wu X L,Guan C W,Sun X M,Ren K 2016IEEE T.Inf.Foren.Sec.11 2706

PACS:05.45.Vx,84.40.Ua,43.38.Si DOI:10.7498/aps.66.020504

SM4 key scheme algorithm based on chaotic system∗

Wang Chuan-Fu Ding Qun†

(College of Electronic Engineering,Heilongjiang University,Harbin 150080,china)

21 August 2016;revised manuscript

6 November 2016)

Block cipher is a widely used encryption method.In order to improve the security of information in the network data encryption systems,the initial key should be guaranteed to be large enough.In order to overcome the threat of quantum computer to short initial keys,a key scheme based on chaotic map is proposed.The chaotic map is introduced into the original SM4 key scheme,which effectively increases the initial key space and greatly improves the resistance to key scheme attacks.

Due to the limited logic resources in hardware implementation,a logistic map is chosen as a chaotic system in this paper.Although the logistic map has many excellent properties of chaotic system,such as initial value sensitivity,randomness,ergodic,etc,there are still a lot of problems that we need to pay attention to.The parameterµis the system parameter in the logistic map.The value ofµcontrols chaotic characteristics in the logistic map.Whenµis equal to 4,the dynamic characteristics of logistic map are best.The values of data transmitted in the network are all quantified as 0 and 1.In order to implement the logistic map in a digital circuit,the digital quantization is needed.The bit sequence design quantization is very simple and saves resource consumption.Compared with other quantization methods,bit sequence design quantization can be implemented in hardware parallelly.United States National Institute of Standards and Technology launched the test program package to test the random numbers.The test program package includes frequency detection,block frequency detection,run test,etc.Those tests are used to detect the randomness in binary sequence of arbitrary length.The test program package proves that the sequence generated by the logistic map has a great randomness characteristic.After the security analysis of logistic map,the hardware implementation of logistic map is carried out in this paper.Based on the theoretical analysis and hardware implementation in the logistic map,a new SM4 key scheme combined with the logistic map is proposed.The proposed key scheme has less hardware resource consumption,larger key space and higher security than other key schemes combined with chaotic systems.The output of key scheme in this paper is tested by the test program package.The results show that the random number produced by new key scheme is larger.In the end,a key scheme attack is introduced in this paper.It is proved that the new key scheme in this paper can effectively resist existing key scheme attacks.

chaos,key scheme algorithm,field-programmable gate array

:05.45.Vx,84.40.Ua,43.38.Si

10.7498/aps.66.020504

∗国家自然科学基金(批准号：61471158)和高等学校博士学科点专项科研基金(批准号：20132301110004)资助的课题.

†通信作者.E-mail：qunding@aliyun.com

*Project supported by the National Natural Science Foundation of China(Grant No.61471158)and the Specialized Research Fund for the Doctoral Program of Higher Education of China(Grant No.20132301110004).

†Corresponding author.E-mail：qunding@aliyun.com